巧用专业软件解决高中几何教学中的难点

丁艺 朱雅婷

【摘要】在高中几何教学中，图形变换中的复合变换一直是教学的难点。传统的板书、幻灯片等形式，要让平均水准的学生掌握图形变化的性质和关系力有未逮。文章介绍了一款专业的几何图形绘制软件，并通过两个教学案例展示了如何交互、动态地展示复合变换的规律，在实践中获得了良好的教学效果。

【关键词】高中几何;图形变换;软件;动态

一、问题的引入

高中阶段的几何教学中，有一些知识点及其运用往往被大多数学生畏之如虎，图形变换特别是涉及几种变换的复合变换，就是其中之一。根据笔者多年的教学经历，在学习单一图形的平移、旋转、反射等变换的时候，平均水准的学生都能较好地掌握，然而一旦涉及几种变换组合起来的复合变换情况，学生往往思路不清，对变换的本质理解不深，无论是在作业中还是在测评中，都易失分。

这主要是因为，使用传统的板书形式只能描绘变换之后的静态结果，如果要讨论若干条件的改变对变换的影响，则需要修改和重绘，费时费力;即便使用一些常规的信息化教学手段，如制作幻灯片并利用一些动画效果，但对学生来说，缺乏互动性和探索性，也无法很快地形成对图形变换本质的理解。

笔者在研究和评估了一些教学辅助手段之后，使用“几何画板”绘制了一些教学示例。“几何画板（The Geometer's Sketchpad，简称GSP）”是一款国内外广泛用于数学、物理教学的付费软件，可运行于Windows和Macintosh操作系统上。笔者除了用几何画板在课堂上给学生动态地展示复合变换，也鼓励学生自己去与之交互、修改和举一反三地编写新的例子。通过几年的教学实践后发现，相较于传统的教学方法，使用几何画板设计展示动态示例，在让学生定性地认识复合变换的效果以及定量地分析几种特殊的变换组合产生的效果方面，后者更具优势。

下面通过两个具体案例来探讨如何基于几何画板进行知识点的动态展示。

二、使用动态展示提高教学效果的案例

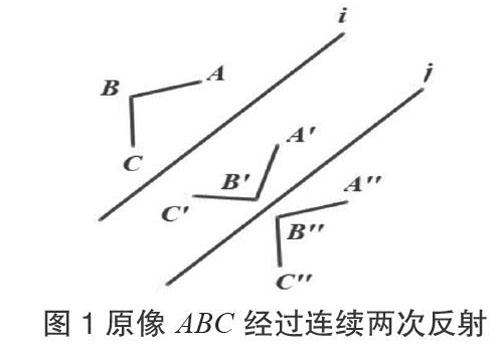
案例1：一个简单几何形状，关于两条平行直线，连续反射两次。

原像关于直线反射，得到图像;关于直线反射，得到图像。

先请学生观察，原像和最后的像之间是什么关系。通过几何画板的演示，移动两条直线和，让学生观察到，象会跟着移动。这使得学生推断得到的关系看起来更加明确。

通过这个操作实例，大部分学生可以判断出，原像和两次反射后的像，是一个平移的关系。

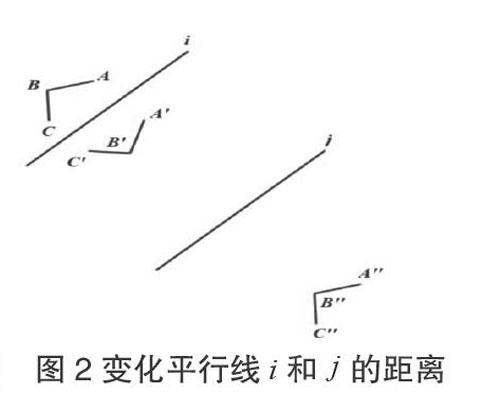
通过测量三個点对、、之间的距离，以及移动两条平行线和，可以看出，三个点对的距离一直保持一致。

于是，笔者请同学们进一步思考：平移是可以通过平移的方向和平移的距离来描述的，那这个平移是否也可以根据某些条件确定呢？

于是有学生猜测，这个平移的距离和两条平行线是垂直的。通过构造直线和的垂线，并且移动图形，可以看出，和是平行的，即，的移动方向是垂直于直线和的。并且进一步可以看出，移动的距离是两条平行线的距离的两倍。无论在几何画板中如何改变平行线和的距离，上述关系始终成立。

由此大部分学生都已经能得出结论：经过两条平行线连续两次反射的叠加效果是平移，并且平移的方向和平行线垂直，平移的距离是两条平行线距离的两倍。

由于是观察图形和与图形交互以后推理并得到验证的结论，大部分学生都能记忆并且较好地理解了多次反射的特点。

案例2：一个简单几何形状，关于两条相交直线，连续反射两次。

原像关于直线反射，得到图像;关于直线反射，得到图像。

笔者请学生观察，原像和最后的像之间是什么关系。通过几何画板的作图演示，并且通过任意改变两条相交直线的角度，像会动态地跟着移动，使这个关系看起来更加明确。

通过这个示例的动态演示，大部分学生已经可以判断出，原像和两次反射后的像是一个旋转的关系，并且猜测很大可能是绕着两条直线的交点旋转的。由此可以进入下一步的验证。

将两条直线的交点标记为，并测量三对点与形成的角度，可以看出，不管怎么移动相交直线和，这三个角度一直保持相等。这就验证了之前的猜测。

于是，笔者启发学生进一步思考：旋转是可以通过旋转中心和角度来描述的，那在这个两次反射构造的旋转中，旋转的角度是什么呢？通过前面的动态展示，学生会发现，和之间的角度随着两条直线之间的交角增加而增加。大部分学生都能给出合理的猜测，这两个角度之间一定有关系。

用几何画板自带的角度测量工具，并且通过动态地任意调整两条直线之间的交角，可以发现量化关系，即和之间的角度一直是两条直线交角（锐角）的两倍。

由此，很多学生已经可以得出结论：经过两条相交直线连续两次反射的叠加效果是旋转，并且旋转的中心是两条直线的交点，旋转的角度是两条直线交角（锐角）的两倍。由于这些结论是学生与笔者一同进行交互性地探索和验证得出的，而非生硬记忆的结论，因此在之后的测评中，都显示学生对这些知识点理解和掌握得相当扎实。

三、结语

板书、手绘作图和测量是高中数学教师的基本功，也是最常规的教学方法。但在有些知识点的教学中，传统手绘的方式需要花费的时间比较长，并且测量距离和角度的结果并没有那么直观地揭示量化关系，也没法任意移动，展示动态的效果。

笔者并不提倡一味地用“信息化”甚至全盘幻灯片化来解决教学中的所有难点，而是选用合适的信息化载具作为常规教学方法的补充。本文所探讨的，使用几何画板展示、教学的这两个案例，既脱胎于常规教学的教案，又利用了专业工具的直观性、交互性、动态性和易操作性，学生很容易掌握使用，几分钟就可以构造出自己的例子，进行计算和验证也非常方便，从而让学生更愿意进行主动探索型的学习，无论从提高教学效果还是从培育学习兴趣的角度，都获得了意料之外又在情理之中的效果。

【参考文献】

孙岚，王红芳.巧用平面几何解决高中数学问题[J].新课程（中学），2016（05）：53.