二次压力梯度三孔渗流模型及非线性渗流特征

余 燕，周琳琅，甘笑非，胡 燕，淦文杰，邓 庄

（中国石油西南油气田公司川中油气矿，四川遂宁 629000）

0 引言

碳酸盐岩储集空间类型多样、孔隙结构复杂，储层裂缝、孔洞发育，具有很强的非均质性［1］。郑松青等［2］针对碳酸盐岩缝洞型储层呈离散介质的特征，提出缝洞网络模型，并在此基础上建立了油水两相流数学模型，简化了储层描述参数，计算成本低，可以进行大规模的工程应用；贾永禄等［3］基于基质、微裂缝、溶蚀孔洞和大裂缝组成的四重介质，建立了缝洞型四重介质的碳酸盐岩试井模型；熊钰等［4］针对大尺度的碳酸盐岩缝洞型油气藏，考虑缝洞的多尺度特征，建立了井打在大尺度裂缝上的裂缝线性流试井解释模型；程飞［5］针对缝洞型碳酸盐岩储层的非均质性和各向异性强的特征，建立了碳酸盐岩油藏储层类型识别模板，并划分了3 种储层类型；姜瑞忠等［6］针对低渗油藏存在的压敏效应和启动压力梯度现象，建立了双重介质低渗油藏的斜井数学模型，并绘制了斜井试井曲线；杜鑫等［7］针对缝洞型油气藏，建立了井筒与溶洞相连通情况下的流动方程并给出了井筒和溶洞之间的压力差表达式；刘建峰等［8］建立了孔洞和裂缝组成渗流空间的典型双重介质模型；王蓓等［9］针对磨溪龙王庙组缝洞型碳酸盐岩储层，建立了多尺度离散裂缝模型，明确了该气藏高、低渗分布区域；姜瑞忠等［10］建立了缝洞型碳酸盐岩油藏水平井分形非线性渗流模型，并结合测井数据将新模型应用于矿场渗流参数的解释，但这些有关碳酸盐岩储层的渗流模型均未考虑二次压力梯度非线性项的影响。

聂仁仕等［11-13］建立了考虑井储和表皮效应的不稳定渗流数学模型，同时，该模型考虑了二次压力梯度非线性项的影响；Nie 等［14］针对底水油藏和厚油层油藏，建立了不同边界条件下考虑二次压力梯度非线性项的球面渗流方程；张林等［15］建立了不同边界条件下考虑二次压力梯度非线性项的三区复合渗流方程；张强等［16］建立了考虑启动压力梯度和二次梯度非线性项影响的渗流模型；Wang 等［17］针对多层复合储层，建立了考虑二次压力梯度非线性项的多区复合非线性模型；Guo 等［18］针对地下地层中气井生产，建立了考虑二次压力梯度非线性项的直井模型；王美楠等［19］建立了考虑启动压力梯度、动边界、二次梯度非线性项的低渗透变形介质油藏渗流模型；Lu 等［20］建立了考虑二次压力梯度非线性项的多孔介质水平井渗流模型。目前，针对碳酸盐岩缝洞型三孔介质储层，尚无有关二次压力梯度三孔渗流模型及非线性渗流特征的研究。

流体在地下储层中的渗流具有二次压力梯度的非线性渗流特性［18-20］，缝洞型碳酸盐岩储层也不例外，采用常规的三孔介质线性渗流模型无法精准描述流体在缝洞型碳酸盐岩储层中的渗流特征。笔者首次建立二次压力梯度三孔渗流模型，研究缝洞型碳酸盐岩储层受二次压力梯度控制的非线性渗流模型的缺失问题，以期实现对缝洞型碳酸盐岩储层渗流特征的精准描述。

1 渗流模型

1.1 物理模型

平面径向流物理模型假设如下：①裂缝孔洞型三孔介质水平等厚地层中心一口井以定产量q生产；②地层厚度为h，地层渗透率为常数且与压力无关，原始地层压力为pi；③井半径为rw，井底压力为pwf；④井到地层外边界的距离为re，外边界可以是无穷大地层、封闭地层或恒压边界；⑤在弹性驱动方式下，黏度为μ的单相液体渗流符合等温达西定律；⑥考虑天然裂缝与井筒沟通，溶洞系统和基质系统中流体均向天然裂缝系统发生拟稳态窜流，因溶洞渗透率大于基质渗透率，故溶洞系统中流体优先向天然裂缝系统窜流；⑦考虑井筒储集效应和表皮效应的影响。

1.2 数学模型及其求解

1.2.1 数学模型

一个完整的数学模型由渗流控制微分方程、初始条件、内外边界条件构成。对缝洞型碳酸盐岩储层，其渗流控制微分方程包括裂缝系统方程、基质系统方程和溶洞系统方程。

（1）渗流控制微分方程

裂缝系统方程：

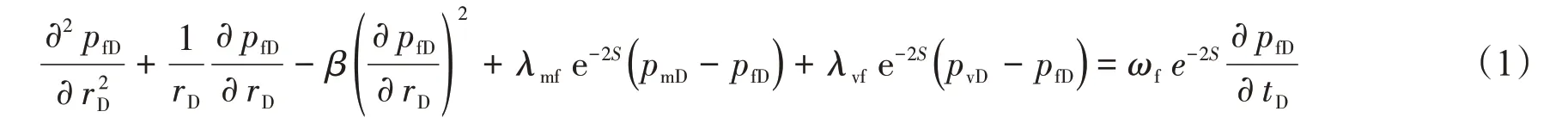
式中：pfD为无因次裂缝系统压力；pmD为无因次基质系统压力；pvD为无因次溶洞系统压力；rD为无因次径向距离；β为无因次二次压力梯度项系数；λmf为基质系统向裂缝系统的窜流系数；λvf为溶洞系统向裂缝系统的窜流系数；ωf为裂缝系统的弹性储容比；S为井的表皮系数；tD为无因次时间。下标f，m，v，D 分别代表裂缝（fracture）、基质（matrix）、溶洞（vug）和无因次（Dimensionless）。

基质系统方程：

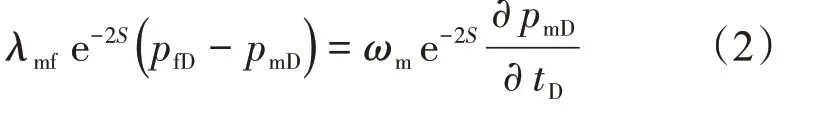
式中：ωm为基质系统的弹性储容比。

溶洞系统方程：

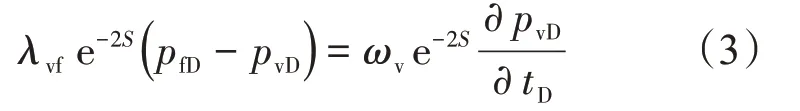
式中：ωv为溶洞系统的弹性储容比。

（2）初始条件

（3）内边界条件

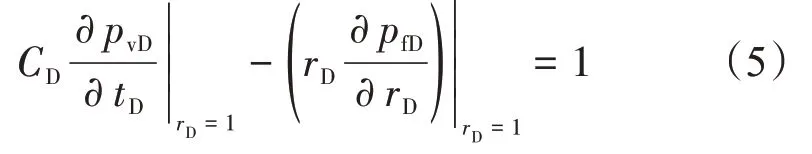
式中：CD为无因次井筒储集系数。

（4）外边界条件

无限大外边界

恒压边界

式中：reD为无因次外边界距离。

封闭边界

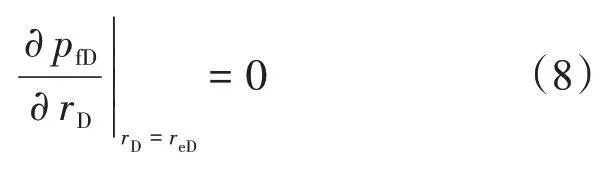
上述数学模型的无因次参数定义如下：无因次压力

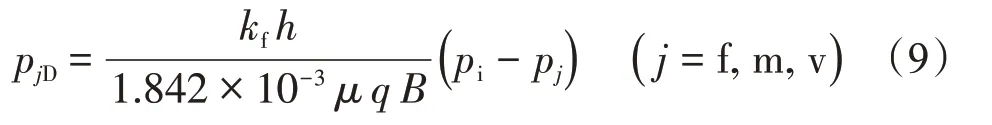
式中：pf为裂缝系统压力，MPa；pm为基质系统压力，MPa；pv为溶洞系统压力，MPa；pi为初始油藏压力，MPa；q为流量，m3/d；μ为黏度，mPa·s；B为地层流体的体积系数，无因次；kf为裂缝渗透率，D；h为储层厚度，m。

基于有效井径定义的无因次距离

式中：r为径向距离，m；rw为井半径，m。

无因次时间

式中：t为时间，h；φf为裂缝孔隙度；φv为溶洞孔隙度；φm为基质孔隙度；Cft为裂缝弹性综合压缩系数，MPa-1；Cvt为溶洞弹性综合压缩系数，MPa-1；Cmt为基质弹性综合压缩系数，MPa-1。

无因次井筒储集系数

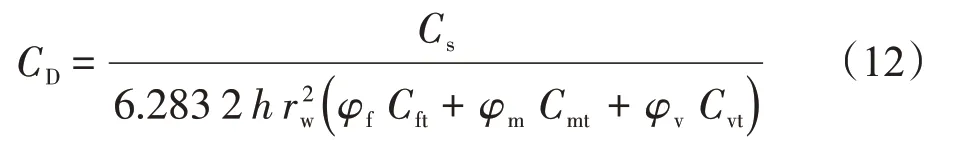
式中：Cs为井的弹性储容系数，m3/MPa。

弹性储容比

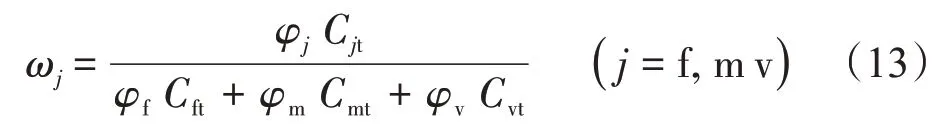
无因次二次压力梯度项系数

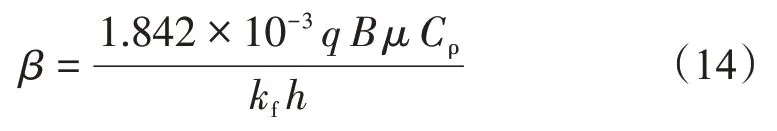
式中：Cρ为地层流体的压缩系数，MPa-1。

1.2.2 积分变换求解模型

引入基于tD的拉氏变换

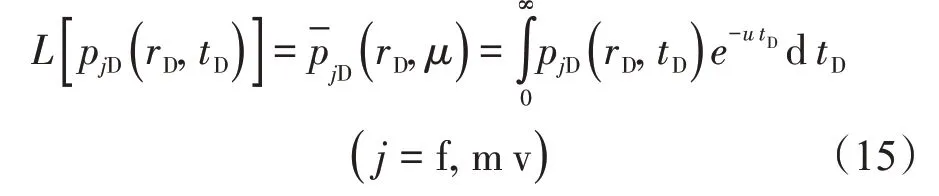
式中：L［］为Laplace 算子为变量pD对应的La‐place 空间变量；u为Laplace 变量。

对式（1）—（3）经基于tD的Laplace 变换后，得

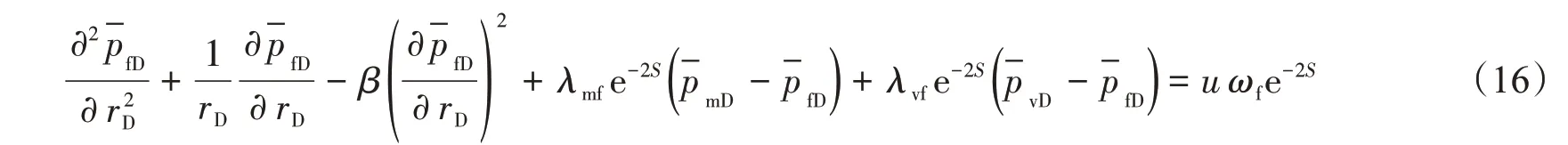
当ωf=1 时，非线性模型则简化为常规单一介模型，式（22）可以简化为质

换句话讲，在相同的油井生产和地层边界条件下，Laplace 空间下的三孔介质模型和均质模型的差异仅仅表现在f（u）的函数表达式不同。因此，如果首先在Laplace 空间中得到均质模型的解，就可以直接通过改变f（u）来得到Laplace 空间下三孔介质模型的解。

先令ωf=1，则考虑单一介质情形，渗流控制方程中就不存在窜流项，则式（1）变为

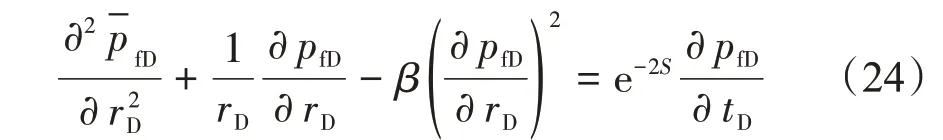
作如下变量代换，将式（24）线性化

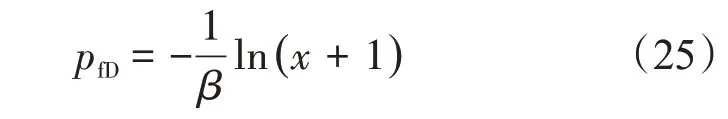
式中：x为无因次裂缝压力的中间代换变量。

再经基于tD的Laplace 变换后，可得到Laplace空间中的数学模型

1.2.3 数学模型的解

用式（22）替换式（27），就可得到经变量代换线性化后的裂缝孔洞型三孔介质渗流偏微分控制方程

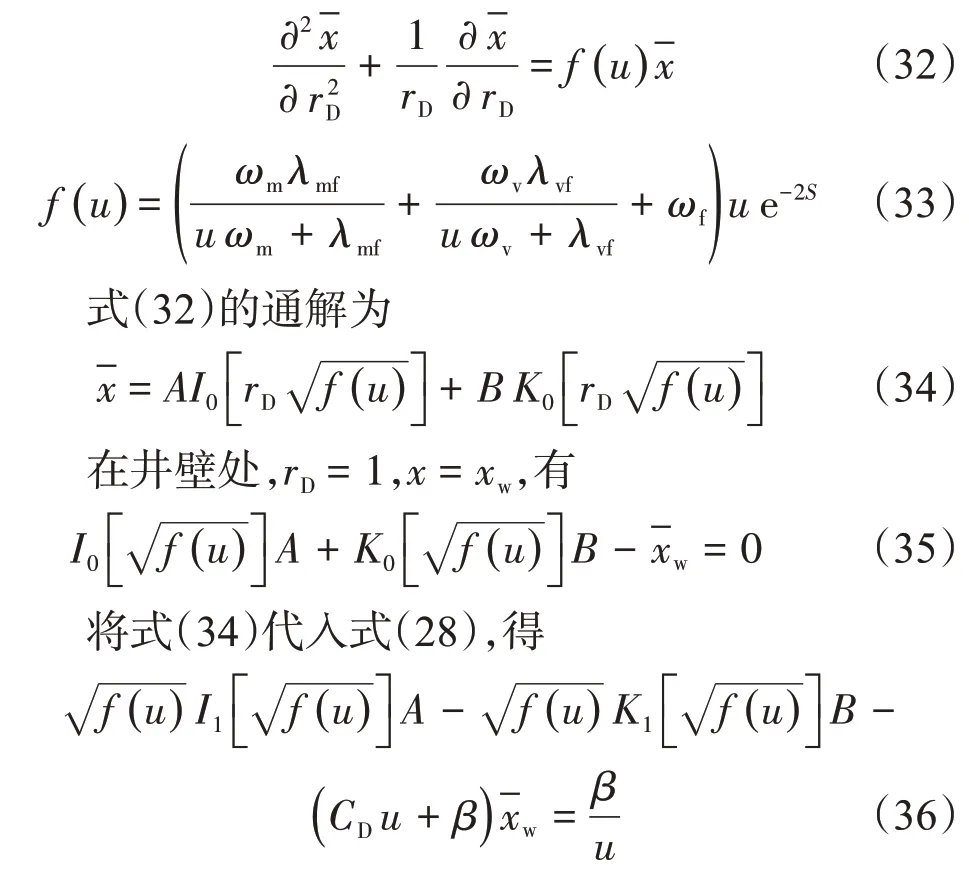
（1）无穷大外边界模型的解

故无穷大外边界条件模型在Laplace 空间的通解为

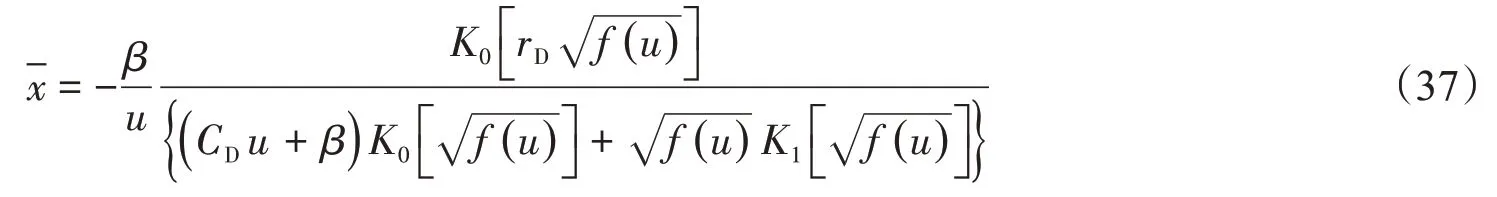
井底rD=1，当p=pwf时，pD=pwD，则x=xw，故无穷大地层模型井底动态压力在Laplace 空间为

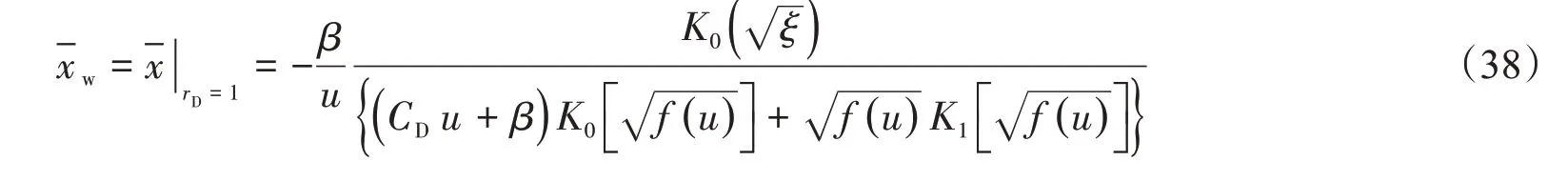
（2）恒压外边界模型的解

将式（34）代入恒压外边界条件式（30），有

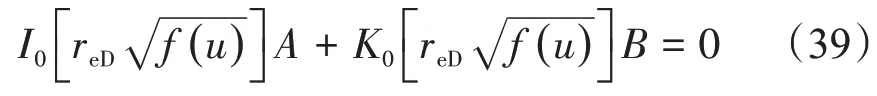
联解式（35），（36），（39），将其写为矩阵形式，利用克莱姆法则或高斯迭代消元法，即可解出系数A和B，从而得出外边界条件为恒压边界时井底压力动态在Laplace 空间的解。

（3）封闭外边界模型的解

将式（34）代入封闭外边界条件式（31），有

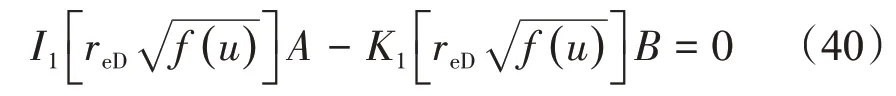
联解式（35），（36），（40），将其写为矩阵形式，利用克莱姆法则或高斯迭代消元法，即可解出系数A和B，从而得出外边界条件为封闭边界时井底压力动态在Laplace 空间的解。

对上述三类外边界条件下Laplace 空间的解，利用Stehfest 数值算法进行数值反演，得到实空间的解xw，再根据压力pD与x的变换关系式，可求出裂缝孔洞型三孔介质非线性渗流模型实空间井底压力动态响应的数值解，进而编程绘制pwD～tD/CD与p'wDtD/CD～tD/CD的无因次双对数渗流特征曲线。

2 非线性渗流特征分析

2.1 非线性渗流过程分析

图1 为受非线性项系数影响的无穷大裂缝孔洞型三孔介质地层拟稳态窜流非线性渗流模型的典型曲线。该曲线主要受无因次二次梯度非线性项系数β控制。在其他参数一定时（CD=10，S=10，ωf=0.001，ωm=0.989，ωv=0.01，λmf=1×10-10，λvf=1×10-8），通过分别设定β值为0，0.01 和0.05，来分析非线性渗流特征曲线与线性渗流特征曲线的差异。当β=0 时，该曲线则蜕化为线性模型的渗流典型曲线（图1 曲线①）。从图1 可以看出，非线性渗流特征曲线向下偏离线性渗流特征曲线，随β增大，偏离量越大。图1 主要有如下7 个流动阶段：

第Ⅰ阶段：纯井筒储集阶段。此流动阶段的曲线特征不受非线性二次压力梯度项的影响。

第Ⅱ阶段：井筒储集和表皮效应阶段。在此阶段，非线性二次压力梯度项的影响开始出现，非线性渗流特征曲线也开始偏离线性渗流特征曲线。

第Ⅲ阶段：早期裂缝径向流阶段。裂缝系统中的流体径向流入井筒，而溶洞系统和基质系统中的流体还未开始流动。与第Ⅱ阶段相比，线性模型和非线性模型典型曲线的差异更为明显。

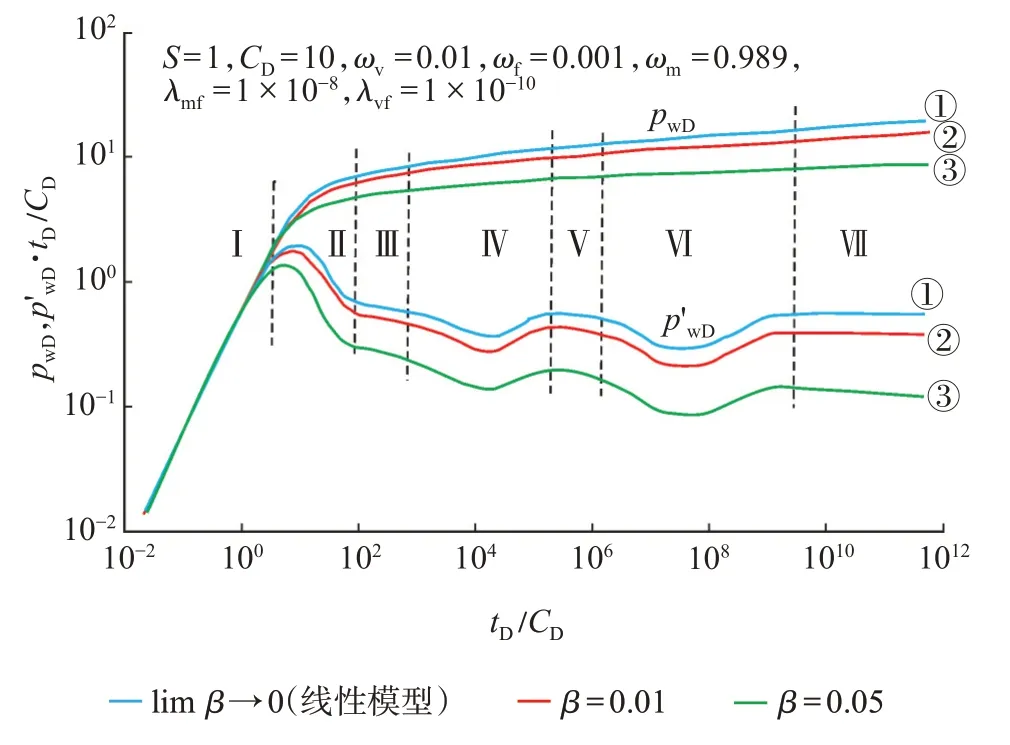
图1 受非线性项系数（β）影响的三孔介质拟稳态窜流模型典型曲线Fig.1 Type curves of pressure transients controlled by varying nonlinear coefficient（β）

第Ⅳ阶段：溶洞系统向裂缝系统窜流阶段。压力导数曲线呈“V 形”，反映了溶洞系统向裂缝系统的窜流。线性模型和非线性模型典型曲线的差异进一步增加。

第Ⅴ阶段：裂缝系统和溶洞系统整体径向流阶段。非线性二次压力梯度项的影响越来越明显，其压力导数曲线不符合“0.5 线”定律，而是位于“0.5线”下方。

第Ⅵ阶段：基质系统向裂缝系统窜流阶段。压力导数曲线呈“V 形”，表明基质系统开始向裂缝系统窜流。线性模型和非线性模型特征曲线的差异越来越大。

第Ⅶ阶段：裂缝系统、溶洞系统和基质系统整体径向流阶段。非线性二次压力梯度项的影响越来越明显，其压力导数曲线不符合“0.5 线”定律，而是位于“0.5 线”下方，随着时间的推移，压力导数曲线逐渐偏离“0.5 线”，如图1 中曲线②和曲线③所示。随着时间的推移，非线性模型的压力导数曲线逐渐偏离线性模型的压力导数曲线。

非线性三孔介质曲线的外边界反映特征与常规线性模型曲线的外边界反映特征类似，此处不再赘述。

该曲线除了受β控制，同时还受别的因素影响。图2 为受溶洞向裂缝窜流的窜流系数（λvf）的非线性渗流模型典型曲线。在其他参数一定时（CD=10，S=1，ωf=0.001，ωm=0.989，ωv=0.01，β=0.05），分别设定λvf值为1×10-7，1×10-8和1×10-9。随λvf增加，溶洞向裂缝窜流时间推迟，在图2 中表现为压力导数曲线的“V 形”向左移动。

图2 受溶洞向裂缝窜流的窜流系数（λvf）影响的典型曲线Fig.2 Type curves of pressure transients controlled by varying inter-porosity flow factor（λvf）

图3 为受基质向裂缝窜流的窜流系数（λmf）的非线性渗流模型典型曲线。在其他参数一定时（CD=10，S=1，ωf=0.001，ωm=0.989，ωv=0.01，β=0.05），分别设定λmf值为1×10-9，1×10-10和1×10-11。溶洞向裂缝窜流时间推迟，在图3 中表现为压力导数曲线的“V 形”向右移动。

图3 受基质向裂缝窜流的窜流系数（λmf）影响的典型曲线Fig.3 Type curves of pressure transients controlled by varying inter-porosity flow factor（λmf）

图4 为受裂缝系统弹性储容比（ωf）、基质系统弹性储容比（ωm）影响的非线性渗流模型典型曲线。其他参数一定时（CD=10，S=1，ωv=0.1，λvf=1×10-10，λmf=1×10-8，β=0.05），分别设定ωf值为0.001，0.01 和0.08，相应的ωm值为0.889，0.89 和0.82。随ωf的增加，在图4 中表现为压力导数曲线的“V 形”变浅、变窄。

图5 为受溶洞系统弹性储容比（ωv）、基质系统弹性储容比（ωm）影响的非线性渗流模型典型曲线。其他参数一定时（CD=10，S=1，ωf=0.001，λvf=1×10-10，λmf=1×10-8，β=0.05），分别设定ωv值为0.01，0.01 和0.5，相应的ωm值为0.989，0.889 和0.499。随ωv的增加，在图5 中表现为压力导数曲线的第1个“V 形”变得更深、更宽，第2 个“V 形”变得更窄、更浅。

图4 受裂缝系统弹性储容比（ωf）影响的典型曲线Fig.4 Type curves of pressure transients controlled by fluid capacitance coefficient（ωf）

图5 受溶洞系统弹性储容比（ωv）影响的典型曲线Fig.5 Type curves of pressure transients controlled by fluid capacitance coefficient（ωv）

2.2 非线性渗流模型典型曲线的偏差分析

为了定量描述非线性项系数的影响，定义绝对偏差（DV）与相对偏差（RDV）：

其他参数一定时（CD=10，S=1，ωf=0.001，ωm=0.989，ωv=0.01，λmf=1×10-10，λvf=1×10-8），分别设定β值为0.01 和0.05，分析非线性项系数对渗流典型曲线的影响（表1—2）。

当β＝0.01 时，由表1 中数据知：当tD/CD＝103时，无因次压力曲线的绝对偏差和相对偏差分别为0.579 8 和8.83%，无因次压力导数曲线的绝对偏差和相对偏差分别为0.085 4 和17.37%；当tD/CD＝107时，无因次压力曲线的绝对偏差和相对偏差分别为1.4 和13.43%，无因次压力导数曲线的绝对偏差和相对偏差分别为0.089 7 和25.40%。

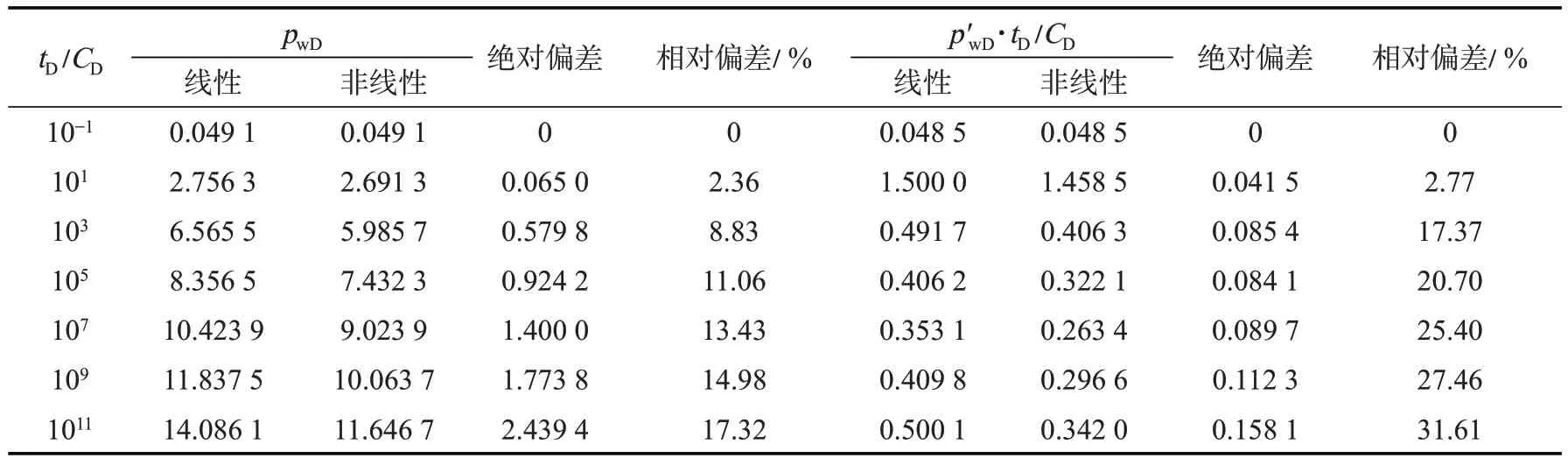
表1 非线性与线性渗流典型曲线的定量偏差数据（β＝0.01）Table 1 Theoretical offset of type curves between the linear and nonlinear models（β＝0.01）

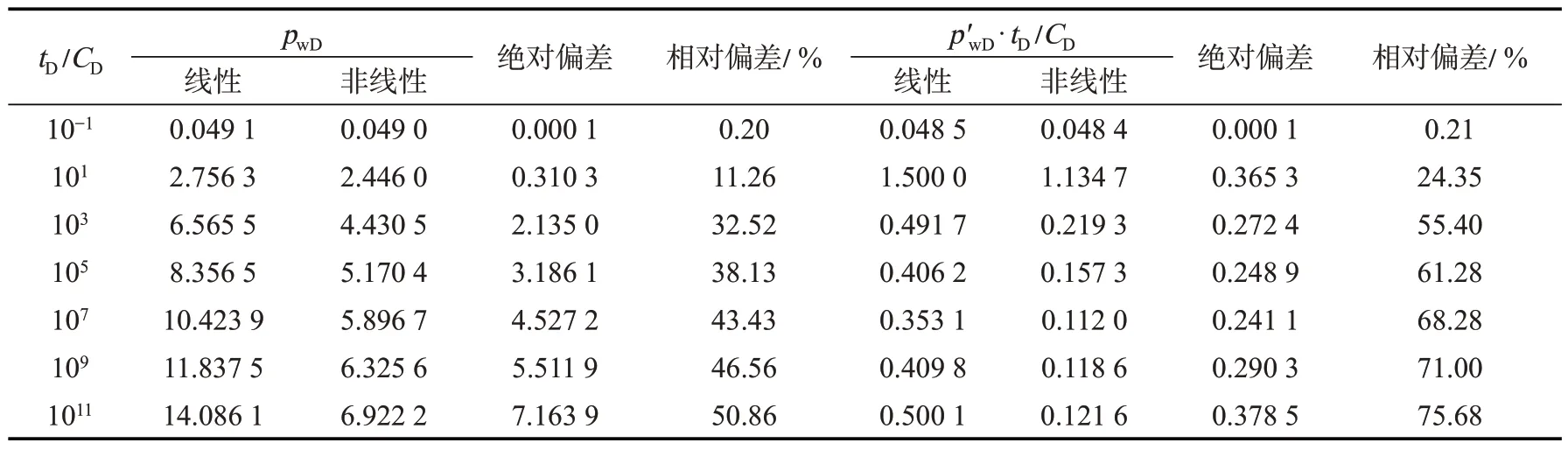
表2 非线性与线性渗流典型曲线的定量偏差数据（β＝0.05）Table 2 Theoretical offset of type curves between the linear and nonlinear models（β＝0.05）

当β＝0.05，由表2 中数据知：当tD/CD＝103时，无因次压力曲线的绝对偏差和相对偏差分别为2.135 0 和32.52%，无因次压力导数曲线的绝对偏差和相对偏差分别为0.272 4 和55.40%；当tD/CD＝107时，无因次压力曲线的绝对偏差和相对偏差分别为4.527 2 和43.43%，无因次压力导数曲线的绝对偏差和相对偏差分别为0.241 1 和68.28%。

绝对偏差和相对偏差均随着无因次时间的增加而增加。在同一时刻，压力导数的相对偏差值大于压力的相对偏差值，例如，当tD/CD＝103，β＝0.01时，压力导数的相对偏差值就（17.37%）大于压力的相对偏差（8.83%）。绝对偏差和相对偏差值均随β的增加而增加，例如，当tD/CD＝103时，β＝0.01的压力相对偏差值为8.83%，而β＝0.05 的压力相对偏差值为32.52%。

3 结论

（1）针对裂缝孔洞型三孔介质储层建立的二次压力梯度非线性渗流模型比不考虑二次压力梯度的常规线性渗流模型能更精准地描述储层的渗流特征。

（2）随油井生产时间的增加，裂缝孔洞型三孔介质储层非线性渗流特征曲线逐渐偏离常规线性渗流特征曲线，且低于常规线性渗流特征曲线。

（3）非线性与线性渗流特征曲线之间的偏离量可用“绝对偏差”和“相对偏差”等2 个参数来定量描述，其偏差随着二次压力梯度非线性系数的增加而增加。当非线性系数为0 时，非线性三孔渗流模型可蜕化为常规线性三孔渗流模型。