地震荷载作用下岩石边坡崩滑响应建模分析
吴 强
(福建岩土工程勘察研究院有限公司,福州 350001)
0 引言
岩石边坡工程又被分为临时边坡工程和永久边坡工程两类。岩石边坡可以看做是地球表面岩石露天侧向地质体工程。在施工过程中面临了大量的崩滑灾害。我国境内多山地丘陵,高原山地占地面积超过我国国土的70%,地质结构和环境客观决定了我国具有大量的滑坡、崩塌、泥石流等灾害。边坡经常会在自身重力的作用约束下,在崩滑过程中产生重大的形变危害。随着我国西部开发和振兴东北经济发展战略的实施,大量的边坡工程开始建设,边坡稳定性成为工程研究的重点问题[1]。
我国处于多个地震带上,很长时间以来均深受地震危害[2]。我国地震的频发性和危害性,对岩石边坡工程产生重要影响[3-4]。现阶段我国针对边坡工程研究所应有的理论和方法,一般以边坡静态时数据为主[5]。因为静态数据大多为固定值,研究相对简单。而边坡动力下的分析就显得更为复杂。边坡动力反应问题对于地震作用下边坡地质防治以及山区土木工程的设计和布局具有重要指导意义。虽然我国目前已经取得了一定研究成果,但是总体来说,水平层次还比较低。虽然自身较为简单,但是结果误差较大,只能应用于较为简单或者精确度要求不高的低帧作用下岩石边坡崩滑动态分析[6-7]。此外还有物理模拟法,就是通过振动台试验,结合物理模型,模拟地震载荷,提取延时边坡崩滑响应数据。这种方法的准确度较高,但是振动实验模型的尺寸需求较大,如果不能达到一定比例,实验结果同样会出现误差,整体耗费巨大。上述分析方法的核心问题在于无法进行动力拆解,对于岩石边坡崩滑响应的分析区域整体化,无法从内外多个方向进行,所以最终的结果误差较大。针对当前研究现状,设计从地震力方向入手,构建二维数据模型,并添加动力条件,从边坡多个方向进行分层影响分析,保证最终分析结果的精确度[8]。
1 岩石边坡崩滑响应分析模型
经过多方证实,竖向地震载荷对于岩石边坡崩滑的作用同样十分明显[9-10]。尤其是震中区域,竖向和水平地震载荷的加速比为0.5到2.5左右,其均值为1.35左右。在地震作用力下,岩石边坡很容易触发倾斜崩滑效应。为了有效研究地震载荷作用下延时边坡崩滑响应关系,设计首先构建一种数值模型。因为岩石边坡崩滑动力响应包括速度、加速度、位移等,即便是同一边坡,不同方向上的相应规律也不同,所以在模型基础上添加动力条件,确定响应规律[11]。
1.1 数值模型的建立
岩石边坡会受到岩性组合、岩体结构等多项影响[12-13]。对其进行数值模拟需要综合考虑多项因素。为了研究地震作用下延时顺岩层边坡动力响应规律,设计构建边坡顺岩层模型,如图1所示。
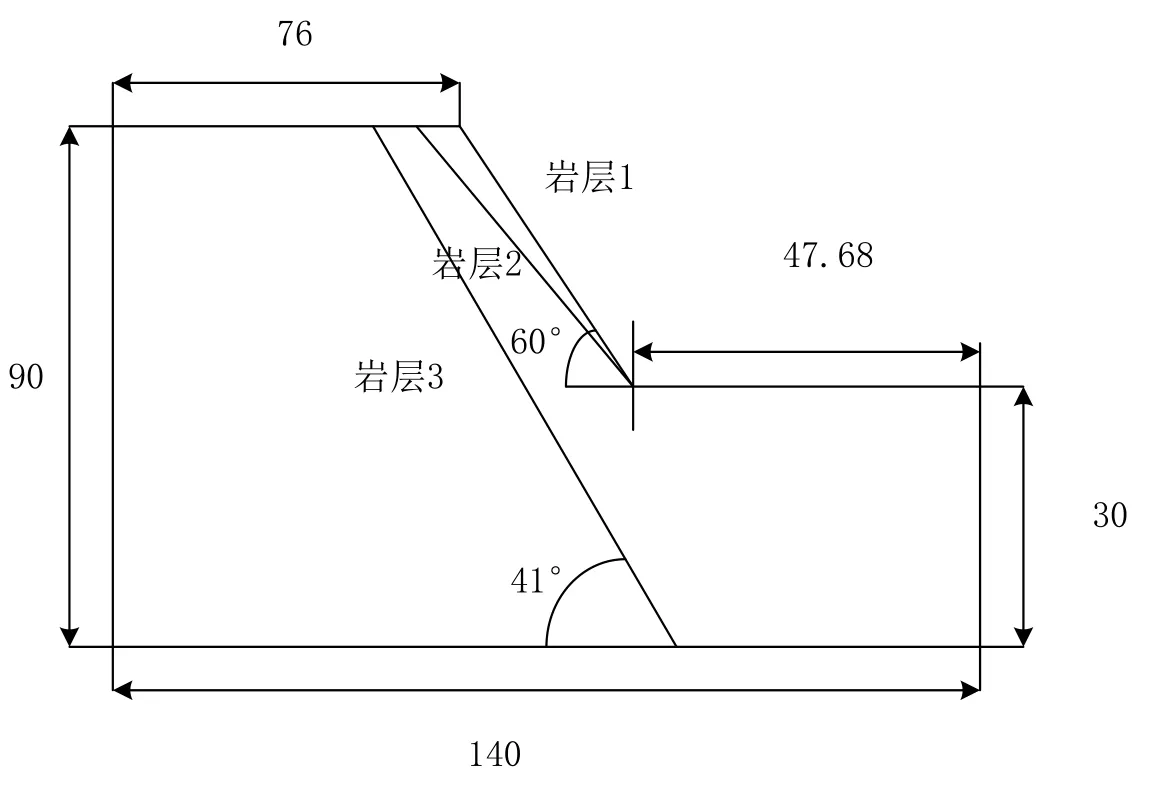
图1 边坡数值模型分析Fig.1 Slope numerical model analysis
设边坡高度为30 m ,倾斜角度为60°,岩层1为强风化岩层,岩体力学作用交第,岩层2位微风化岩层,岩层3位基础完整岩层,坡顶存在少量的载荷裂隙。设定物理学参数表如下:

表1 数值模型物理学参数表Table 1 Physical parameters of numerical model
为了有效提高当前地震载荷以及作用地震波可以在数值模型内部进行有效船舶。设计将模型数据最大网格尺寸设定为1 m。模拟材料以边坡常用模拟的碳素本构材料,强度准则为标准化强度准则,两侧需要标定横波延伸边界,可以有效避免地震载荷数据因为回弹产生差异划分误差。阻尼数据需要标定局部范围,一般情况下阻尼系数设定为0.158。开始时需要先计算边坡静力数据,引入边界动力条件进行数据分析[14]。在模型基础上设定数据分析点,对地震载荷下边坡速度的影响规律进行监测。设计按照固定间距,每组设定A到G7个监测点,破内距离25 m横向设定V1到V6,6个监测点。坡顶距离8.38 m处设置H1到H9,9个监测点。同时为了证明当前地震载荷的边界作用条件正确,在模型底端左右两侧分别设置了统一的加速点,速度监测点。通过分析当前模型顺岩层边坡各监测点在地震载荷下的PGA放大系数、位移制动变化和塑性区变化,可以得到当前边坡响应数值[15]。
1.2 动力条件输入
在上述数值模型的技术上,将地震载荷以射角a入射角传入到边坡,根据力学作用特征可知,P波在其传输方向上会产生两个载荷分量分别为Fpsina和Fpcosa。其中,FpSina将产生水平加速度,而Fpcosa会产生数值加速度。同理将地震载荷的S波传输方向进行解析,同样会产生两个载荷分量FSsina和Fscosa。FSsina产生竖向加速度,而Fscosa则产生水平加速度。当P和S波分别引入数值模型后,根据竖向加速度和力学分量会产生及速度分量组合。如图所示。
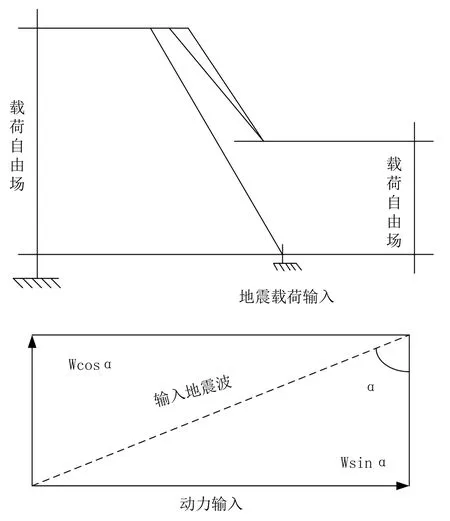
图2 地震耦合作用下数值模型边界条件Fig.2 Boundary conditions of numerical models under seismic couplingg
随着地震载荷距离的不断叠加,P波S波同时作用在边坡,水平增加速度分量由Fpsina和Fpcosa组成,竖向加速度由力量分量组成。因为随着P波和S波的传输速度差异,会导致其产生边坡时间差Δt,

在公式中,r表示地震震源距离,Vp为地震纵波波速;VS表示地震横波波速。
在实际作用下,地震载荷的P波会直接作用到边坡下端,经过时间Δt后,S波直接作用达到边坡,所以对于某一时刻t来说,边坡会产生竖向加速度的地震作用力分量为:
Fpcosα⋅t0+Fssinα⋅(t0-Δt),而产生水平加速度的地震作用分量为:
Fpsinα⋅t0+Fscosα⋅(t0-Δt)。由此可以得出以下关系式:
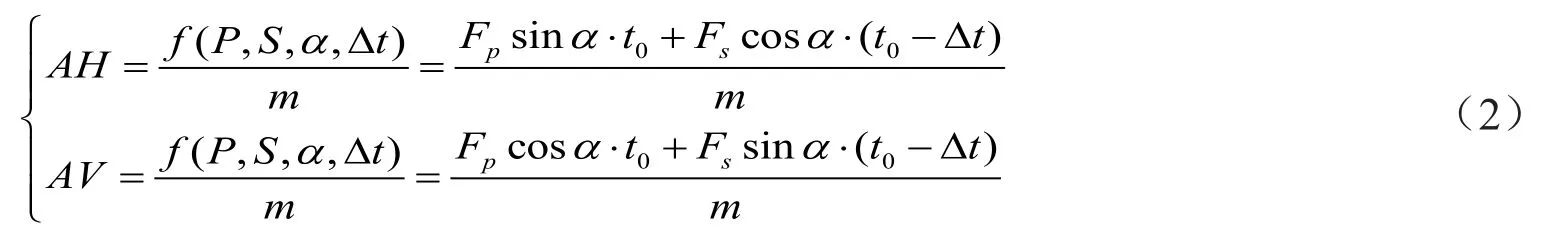
在公式中,t0为P波作用下的累积作用时间,t0-Δt表示当前S波作用边坡的累积时间,m表示地震载荷作用下的边坡质量。
因为此次设计的模型边坡数据靠近震中,P、S波垂直接近模型底部。所以需要添加模型横向加速,且所有加速均有P波产生。根据国家地震中心对于地震载荷的严格规定,所以设计选取神户模拟监测站,作为地震输入。P波的峰值设定为0.55 g,对滤波和基线进行矫正,并输入时间间隙18 S,调整地震P波的加速线程,调整流程如下:

图3 加速线程调整流程Fig.3 Accelerate thread tuning process
设S波的博峰值加速度调整为0.125 g,对其进行滤波和基线矫正,持续输入时间保持在15 s左右。调整后确定S地震波的实际曲线。具体定位波动公式如下:

其中,y表示剪切波的真实值,kx表示纵波平面。则有:

此时纵波速度可以确定为Vp=6 km/s;横波速度表示为Vs= 3 km/s。所以根据上述模型公式,可以确定时间传播差异性为2.25 s,也就是模型地波的输入P波竖向加速度延迟2.25 s左右,由此可以进一步推导S波的水平加速度。根据数据模型,可以分析当前地震载荷作用下多方向的地震岩石边坡崩滑响应规律。
2 基于数值模型的边坡崩滑响应规律分析
依靠上述建立的数值模型,可以对地震载荷作用下延时边坡崩滑失稳过程中的相应特性和变化规律进行分析。分析过程包括多个方向,保证分析的最终准确度。
2.1 岩石边坡崩滑上方向响应特征
图4为当前模型下,坡面监测点水平振动和耦合震动下的时程曲线。通过坡面跟踪设置检测点A和G,检测位移时程。

图4 位移响应振动时程曲线Fig.4 Displacement response vibration time history curve
如图所示,随着地震波开始趋于稳定,坡面上位处在不同岩性位置的变化趋势开始重叠。第一阶段坡面上侧G监测点显示,岩石边坡的位移变化很小,这是因为地震波振动较小导致的,通过对监测点位置变化和结构面分层,构建结构面的基本弹性振动。振动结束后,分析是否存在弹性截面。根据坡顶出现的放大效应,构建地势分析表格,证明岩体结构面岩质边坡的动力反应控制作用。
根据控制作用力,制定极化象限,可以确定耦合作用时的崩滑响应数据,确定竖向地震力边坡的破坏作用。传统响应分析仅考虑水平振动,忽略竖向振动,并不能完全提取边坡动力响应,所以才会产生误差。此外边坡模型结构面会增长,在耦合作用下,结构面的位移增长量需要根据上述设计的数值模型进行计算,并需要引入波长入射角和相位差因素,提取上方向规律分析数值。
2.2 岩石边坡崩滑水平方向响应特征
为了更好分析提取延时边坡崩滑水平方向的分析特征,除了上述数值模型以外,还需要定义坡体内部动力响应下的加速峰度值PGA和坡体内部数值模型监测点H8的动力响应加速度峰值比值,如图所示。
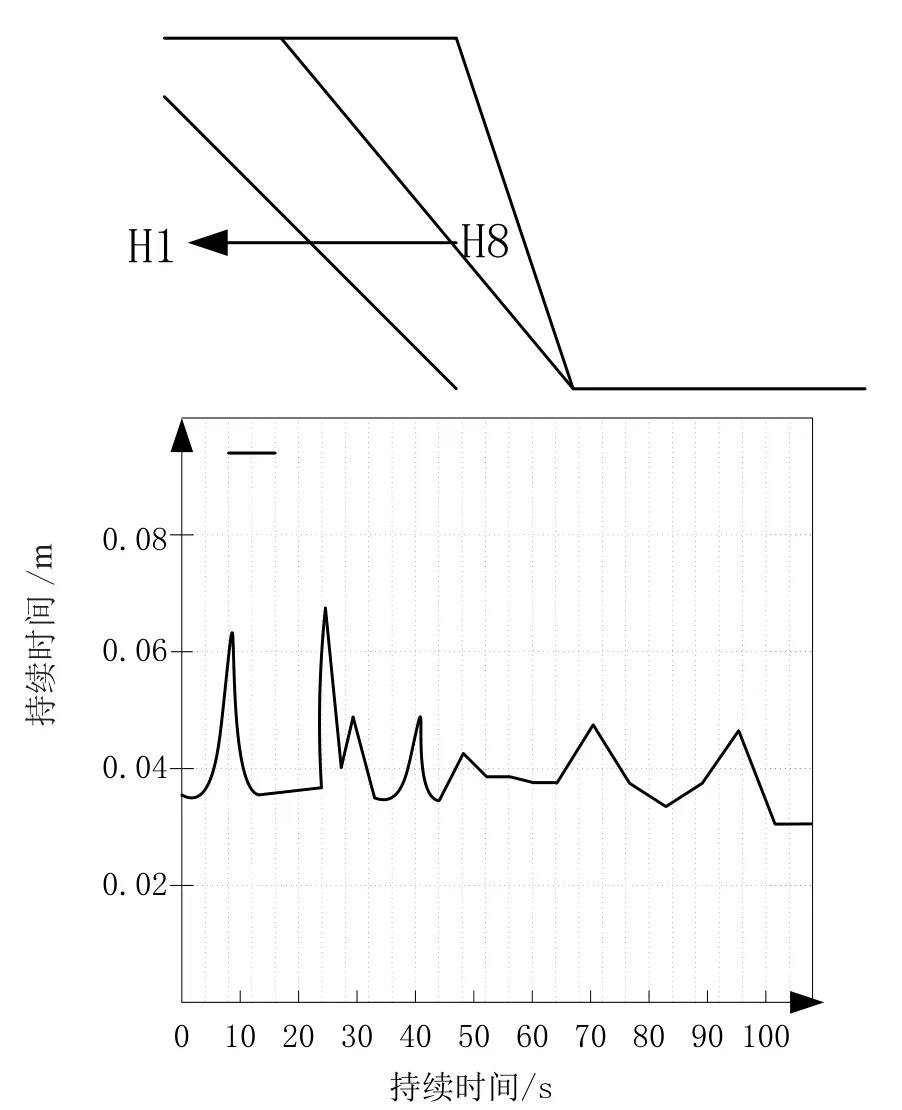
图5 位移响应振动时程曲线Fig.5 Displacement response vibration time history curve
图5包括H1到H8多个监测点,显示了坡体内部水平布置监测点位移时程变化。在模型基础上引入PGA放大系数可以确定,水平地震作用下耦合地震载荷随着距离增加的相应变化情况。因为岩层2和岩层3分属不同的结构面,竖向波和水平波地震反应截面之间容易出现小范围波动。由此可以确定放大系数之间的耦合作用距离。此外应用PGA放大系数和数值模型,仅对300米距离有效,超过此段距离的数据需要重新测算。
3 实验数据分析
上述依靠数值模型的多方向建模分析方法能否真正有效反映地震载荷作用下岩石边坡崩滑响应规律,需要进行仿真实验分析论证。
3.1 实验数值模型及环境搭建
实验验证模型的边界条件、单元分割、网格尺寸包括地震载荷差异输入均按照常规实验标进行。三维数值坡比为1:0.3,图6位数值模型样本。
图6 数值模型实验图Fig.6 Numerical model experimental diagram
在对地震载荷岩石边坡崩滑的分析中,虽然内摩擦角、滑移量均为重要的评估分析指标,但是因为室内实验环境的局限性,实验最终选定粘聚力作为响应建模分析的实验判定指标。为了判定上述分析模型的优势性,实验选择传统AGA模型作为数据参考。在实验模拟环境下,仿真地震载荷,对边坡粘聚力进行分析测评。实验导入数据如下:

表2 实验导入数据Table 2 Experimental import data
在上述实验环境下进行数据提取,按照工程类比原则使用实验设定的两种模型对地震载荷影响下的边坡崩滑粘聚力进行测评验证,结果如下:

表3 粘聚力测评结果Table 3 Cohesion test results
实验从边坡三个方向选择A、B、C三个基点作为数据参照,进行粘聚力测评。根据测评结果不难看出,上述设计模型的粘聚力测评结果均在7.0以上,而传统AGA模型则维持在4左右,二者出现明显差异,直接证实了设计模型的数据准确性。
4 结语
首先归纳和整理了当前岩石边坡崩滑研究数据,建立数值模型分析体系,结合当前实际情况输入动力条件。依靠完整数值模型从多个方向分析研究岩石边坡的崩滑数据,确定最终的数据范围,实验证明了当前数据的真实有效性。

