广西北流—广东化州5.2级地震及前震的矩震级测定

洪玉清,杨 选,龚 萱,马晓静,蒋 策

（1. 广东省地震局,广州 510070；2. 中国地震局地震监测与减灾技术重点实验室,广州 510070；3. 广东省地震预警与重大工程安全诊断重点实验室,广州 510070）

0 引言

2019年10月12日22时55分在广东化州与广西北流交界发生由两个事件相互重叠构成典型的同源重叠地震。广东地震台网速报结果为：前震ML4.2发生于24.59秒纬度22.26°经度110.54°深度是13 km ,主震MS5.2发生于26.66秒纬度22.15°经度110.52°深度是10 km,地点为广东化州。速报地震工作中依据《地震速报技术管理规则》被统一命名为广西北流5.2级地震,之后正式编目时修定为：前震MS4.6发生于24.59秒纬度22.155°经度110.535°深度是13km, 主震MS5.1发生于26.66秒纬度22.149°经度110.541°深度是9 km,参考地名修改为广西北流、广东化州交界。

对于发震时刻接近的两个或多个事件,台站记录波形相互叠加,对每个地震事件的参数测定带来较大影响。王登伟[1]对重叠地事件进行了分类,给出了同源重叠事件的主要识别依据；冯雪玲等[2]利用小波包变换识别地震波形叠加的起始时刻,从而实现叠加地震事件的分离；李璐等[3]、谭毅培等[4]、马晓静等[5]利用匹配滤波技术,以历史地震事件为模板,在叠加波形中搜寻与模板相识的事件,该方法在处理余震系列和震群时具有较大优势,且能提高震相到时的捨取精度,特别是使用张淼等[6]的匹配滤波技术能同时匹配定位确定地震大小,但是由于前震和主震两个地震仅差约2s,这种高度重叠事件震幅相互叠加,尤其影响后面地震的震级测量精度。本文将以此次重叠事件为例,尝试通过理论地震波在台站端叠加后与实际地震波形进行比较来确定前震及主震的标量地震矩,进而确定矩震级,以此来探索重叠地震震级的测定问题。

1 原理方法

若ui1(t)前震t时刻在i台的位移,ui1(t)主震t时刻在i台的位移,则依据地震波的可叠加原理,前震与主震传播到台站i的等效位移ui(t)可按(1)式获得。

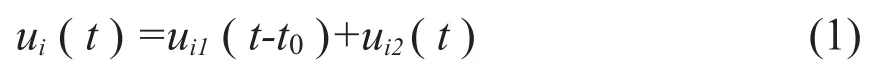
其中t0为主震与前震的发震时间差。再用巴特沃斯滤波器把实际波形与叠加获得的理论波滤波到同一频段,截取一定长度的实际波形段,按（2）式计算该波形段与对应理论波形段的偏差和ei。

上式中tstart和tend分别为截取波形段的起止时间,Δt为理论波形段和实际波形段互相关确定的时间平移。

在震源的走向、倾向和滑动角已知时,按（3）式确定地震矩Mi,合成不同矩震级对应的理论波形,计算对应的偏差ei,搜索ei极小值对应的矩震级,即为第i台的矩震级Miw,各台站矩震级的算术平均值即为此地震矩震级Mw。

2 资料

2.1 实际观测波形数据预处理

本文选取重叠地震震相记录简单清晰且信噪比较高的16个近台（见图1）实际波形进行预处理,去除倾斜和均值,再扣除仪器响应,然后积分为位移记录,滤波后通过坐标变换将E、N分量数据转换为径向（R）和切向（T）数据。考虑到波形的长周期部分受背景噪声影响相对较小,应该选用长周期部分进行震级搜索,但同时考虑到前震和主震发震时刻不足2 s ,因此在滤波器的选取上,决定采用频带为0.02～0.5 Hz的5阶巴特沃斯带通滤波器滤波,既可以滤除大部分噪声,又可以保留能反映出两个地震相互叠加这个信息。

2.2 震源机制

前震初动较易读取,共获得64个分布较好较为可靠的初动方向,运用F0CMEC方法获得其震源机制解,见表1。主震由于受前干扰初动不易读取,通过比较XNY、GAZ等近台的初动,初步认为两个地震的震源机制相同[7]。

表1 前震震源机制解Table1 Focal mechanism solutions of foreshocks

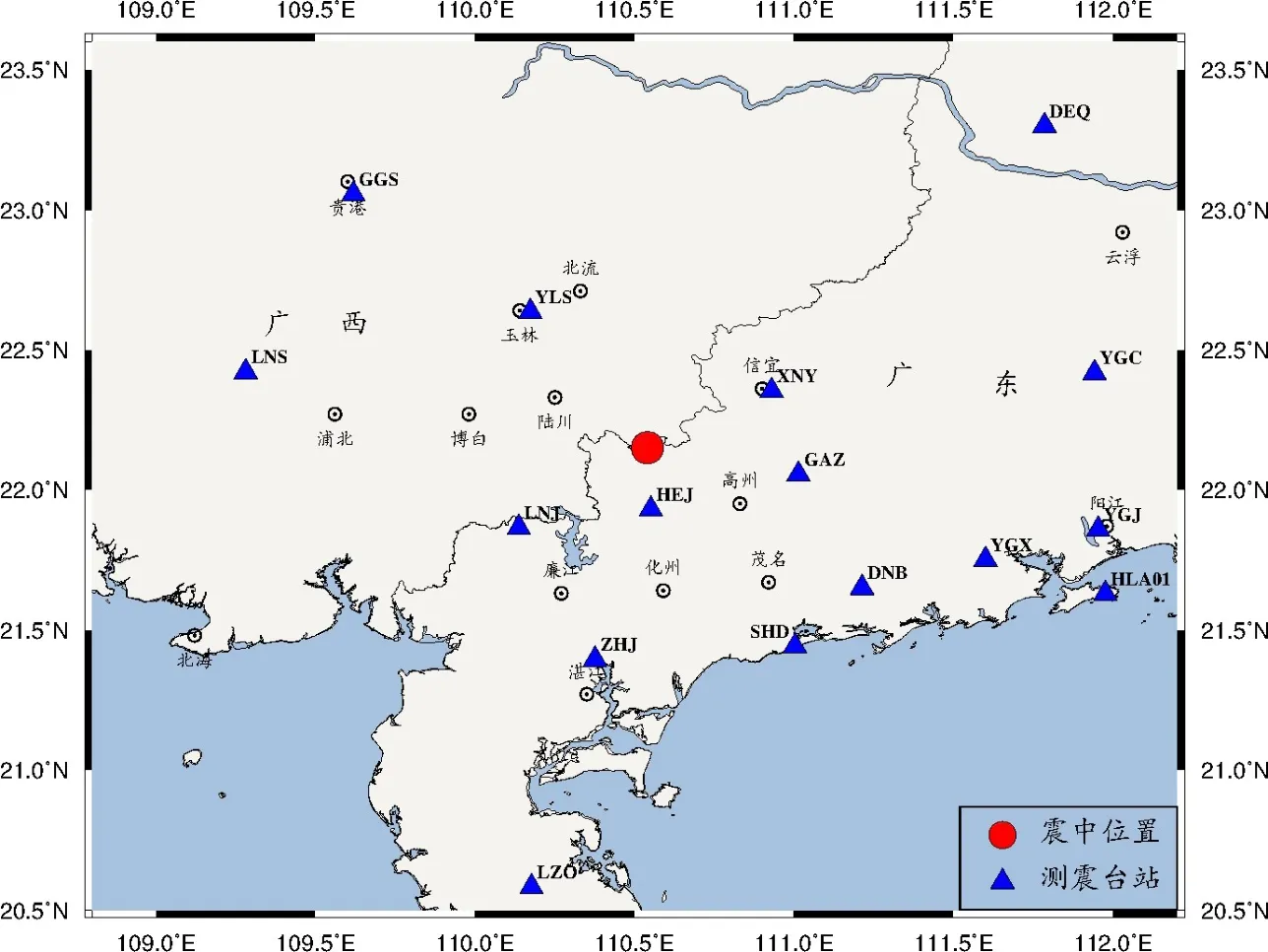
图1 震中及台站分布图Fig.1 Distribution map of epicenters and stations

2.3 速度模型及理论波形

本文采用汪荣江等开发的Qseis2006b程序[8-9]合成理论波形。程序中使用的速度模型为带有沉积层的crust2.0模型（表2）,震源机制解为运用F0CMEC方法计算得到的震源机制解（表2）,地震位置参数采用广东省地震台网中心统一编目结果。

表2 速度模型Table 2 Velocity modle

3 前震矩震级测定

根据地震编目结果可知前震和主震发震时刻相差2.07 s；但是通过读取震相清晰台站的初至到时发现两个地震初至P波到时差为1.77 s,此到时差基本不随震中距离变化,其它的同组震相也具有此特征,这是同源重叠地震的典型特征之一。因此确定各台站从初至波到达到开始1.7 s的波形数据只与前震有些关系,选择理论P波初至开时长1.70s的信号,分别与实际P波初至前后0.5s的实际波形做互相关,相关系数最大时,利用（2）式求取该台站该震级对应理论波形P波段和实际波形P波段的偏差和。以矩震级MW3.80～4.80为搜索范围,0.02级为搜索步长,得到搜索范围内各矩震级对应的偏差和,拟合偏差和,呈现抛物线状,抛物线最小值点对应矩震级,即为该台站的矩震级。

图2 前震震级测定时各台站理论波形与实际波形拟合误差曲线及各台站测定矩震级时的波形拟合图Fig.2 The fitting error curve of theoretical waveform and actual waveform of each station and the waveform fitting diagram of moment magnitude measurement of each station when the foreshock's magnitude is measured

我们选择相关系数大于0.85、信噪3倍以上的台站,同时查看波形拟合图,去除互相关时产生错误的高互相关系数,但实际上理论波形和实际波形相似程度不高的台站,得到HEJ等10个台站（见图2）,读取每个台站矩震级（见表3）,平均为4.16 ,前震矩震级MW为4.2。

表3 各台站测定的前震矩震震级Table 3 The foreshock's magnitude measured by each station.

4 主震矩震级测定

上一步已确定的前震理论波形,分别与不同矩震级对应的主震理论波形按1.77 s到时差叠加,从而获取前震与主震相互叠加的合成理论波形。因为初至S波很难提取准确,所以改为截取的合成理论S波中最大幅值前后各2 s的波形,与实际波形最大幅值处前后各2 s ,在实际最大S波幅值前后滑移,并分别做互相关,相关系数最大时,按（2）式求取偏差和。由于从波形就直观显示主震震级要大于前震震级,因此选择主震矩震级搜索范围为每个台站前震矩震级开始到Mw5.10截止,仍以0.02级为搜索步长,拟合偏差和,曲线呈现抛物线状,抛物线最小值点对应震级矩,即为该台站的矩震级。

图3 主震震级测定时各台站理论波形与实际波形拟合误差曲线及各台站测定矩震级时的波形拟合图Fig.3 The fitting error curve of theoretical waveform and actual waveform of each station and the waveform fitting diagram of moment magnitude measurement of each station when the main shock's magnitude is measured

我们选择相关系数大于0.60、信噪比3以上的台站,同时查看波形拟合图,去除互相关时产生错误的高互相关系数,实际上理论波形和实际波形相似程度不高的台站,得到HEJ等7个台站（见图3）,读取每个台站矩震级（见表4）,平均为4.70 ,主震矩震级MW为4.7。

表4 各台站测定的主震矩震震级Table 4 The main shock's magnitude measured by each station.

5 结语

（1）前震矩震级为Mw4.2 ；在测定过程中,震源机制以及使用的波形资料都是没受主震干扰,其结果应该可靠的。在考虑消除前震影响后,主震的矩震级测定为Mw4.7 ,比前震大0.5级。

（2）通过理论波形的叠加,再利用理论波形与实际波形拟合方法,可以将重叠地震区分,震级测定时消除相互影响,从而使地震的大小得到更加准确。

（3）为了保留能反映两个地震相互叠加的信息,选用的巴特沃斯带通滤波器高频端使用到了0.5 Hz ,由于高频成份对速度结构、衰减因子、地表地形起伏等因素都较为敏感,这些因素在震级测定时具体定量影响还值得进一步研究。

致谢：计算理论地震波形时使用了德国波茨坦地学研究中心（GFZ）汪荣江研究员的Qseis2006软件,在此表示感谢!