混凝土单轴压缩破碎分形研究

吴剑锋，李慧剑，王彩华，孟德亮，李佶芩

(1.燕山大学河北省重型装备与大型结构力学可靠性重点实验室，秦皇岛 066004；2.东北石油大学秦皇岛校区，秦皇岛 066004)

0 引 言

混凝土作为一种典型的人工多相复合材料，内部随机分布大量的孔隙、裂纹等细观损伤结构[1-4]，其分布状态与几何形状在一定测度范围内具有明显统计自相似性[5-8]，因而，在其形成和工作过程中均表现出了一系列的分形特征[9]。借助分形[10]这一数学工具，既可以对混凝土在不同尺度下的力学行为进行较为合理、准确的把握，又有助于认识混凝土宏观形式上所表现出来的随机性和非线性等特征。

研究人员围绕混凝土等准脆性材料的破碎块度分形开展了相关研究，谢和平等[11]系统介绍了将分形理论引进到岩石断裂和破碎研究的成果。高峰等[12]通过标准岩样的单轴压缩实验，着重对岩样破碎后的碎块块度分布进行了统计分析。赵昕等[13]利用高温后的混杂纤维UHTCC材料的动态压缩试验，对冲击破碎后的试样进行了破碎分形特征分析。任韦波等[14]通过对高温后的素混凝土和玄武岩纤维混凝土进行冲击荷载试验，研究了冲击破坏后试件破碎块度分布的分形特征。施劲松等[15]通过对混凝土进行不同温度下的冲击压缩试验，分析了温度对碎块分形维数的影响。尹越刚等[16]通过对混凝土进行不同应变率下的冲击压缩试验，研究了冲击破坏后的混凝土试件碎块的尺度分布规律和分形特征。

综上可见，针对混凝土单轴压缩破碎分形特征的研究较少，因此，本文将通过混凝土单轴压缩试验，基于Turcotte研究理论对混凝土破碎后的分形特征进行研究。分析粗骨料粒径、试样形状对混凝土破碎分形维数的影响，探讨抗压强度、峰值应变、单位体积吸收能、脆性指标与破碎分形维数的关系，为混凝土破碎分形研究提供参考。

1 实 验

1.1 试样制备

试验所用水泥为秦皇岛市浅野水泥有限公司生产的P·O 42.5(R)普通硅酸盐水泥，表观密度3 030 kg/m3；粗骨料采用抚宁石灰岩碎石，粒径范围为5～10 mm、5～16 mm(5～10 mm和10～16 mm各50%)、10～16 mm，表观密度2 730 kg/m3；细骨料采用青龙天然河砂，细度模数为2.79，普通中砂，最大粒径为5 mm，表观密度为2 580 kg/m3。混凝土配合比见表1。混凝土的搅拌通过无锡建材设备机械厂生产的JW-60单卧轴试验室搅拌机完成。混凝土的振捣利用无锡建仪仪器机械有限公司生产的ZHDG-80磁性振动台实现。试验所需试样为40 mm×40 mm×160 mm的棱柱体(浇筑成型)和约100 mm×50 mm圆柱体(钻芯成型)(对应编号为LZ10、LZ5、LZ0和YZ10、YZ5、YZ0，其中10、5、0代表粗骨料粒径分别为5～10 mm、5～16 mm和10～16 mm，LZ代表棱柱体，YZ代表圆柱体)，所有试样均静水养护28 d，然后在室内自然放置300 d后进行试验。

表1 混凝土的配合比Table 1 Concrete mixture ratio

1.2 试验设备与方法

试验利用上海衡翼精密仪器有限公司生产的HYWE-100060微机控制电液(伺服)万能试验机，参照《普通混凝土力学性能试验方法标准》对试样进行单轴压缩加载，加载过程采用力控制方式，加载速度为0.3 MPa/s，直至试样破坏。试样变形使用钢铁研究总院钢研纳克检测技术有限公司生产的YYU-10/50电子引伸计测量。筛分试验采用筛孔边长为0.6 mm、1.18 mm、2.36 mm、4.75 mm、9.5 mm、13.2 mm、16 mm的标准砂石筛，对破碎后的混凝土碎块进行筛分，称量各级筛分质量。

2 结果与讨论

2.1 混凝土碎块分形维数计算

依据Turcotte[17]研究成果，混凝土碎块分形维数D可由碎块粒径r和大于该粒径的碎块数目N表示。

N∝r-D

(1)

对式(1)求导，可得:

dN∝r-D-1dr

(2)

粒径为r的碎块筛下累计质量M(r)和碎块总质量M(T)满足式(3)关系。

(3)

式中，rm为碎块最大粒径尺寸，b为碎块分布参数。

对式(3)求导，可得:

dM(r)∝rb-1dr

(4)

又因碎块数目增量与碎块质量增量符合式(5)关系。

dN∝r-3dM(r)

(5)

所以，联立式(2)、(4)、(5)，可得：

r-D-1∝r-3rb-1

(6)

进一步整理可得:

D=b-3

(7)

式(7)表明，混凝土碎块分形维数D可通过碎块分布参数b得出。

2.2 ln[M(r)/M(T)]-lnr曲线

对式(3)两边取对数，可得:

ln[M(r)/M(T)]=bln(r/rm)

(8)

式(8)表明，碎块分布参数b即为ln[M(r)/M(T)]-lnr曲线斜率，为此可通过绘制双对数ln[M(r)/M(T)]-lnr曲线，求出碎块分布参数b。本试验各试样的ln[M(r)/M(T)]-lnr曲线见图1。

从图1可以看出，对于圆柱体试样和棱柱体试样，试验数据在双对数坐标下，均表现出了良好的线性相关性，说明压缩破坏后的混凝土碎块分布满足统计意义上的自相似性，具有分形特征。这是因为，混凝土内部细观裂纹、孔隙在不同尺度上具有自相似性，而破碎过程与碎块形状又是裂隙扩展的直接结果，因而导致碎块尺度分布具有幂律特征，混凝土碎块分布是一个统计意义上的分形。

图1 ln[M(r)/M(T)]-lnr关系曲线Fig.1 Relation curves of ln[M(r)/M(T)]-lnr

2.3 讨 论

2.3.1 粗骨料粒径、试样形状对混凝土破碎分形维数的影响

为考虑粗骨料粒径及试样形状对混凝土破碎分形维数的影响，本文进行了三种粒径(5～10 mm、5～16 mm、10～16 mm)及两种形状(棱柱体、圆柱体)的对比试验。图2给出了粗骨料粒径及试样形状对混凝土破碎分形维数的影响。由图可知，除5～16 mm粒径圆柱体试样因样本个性原因外，两种形状试样的破碎分形维数均随粗骨料粒径的增大呈降低趋势，对于棱柱体试样，5～10 mm粒径试样的破碎分形维数是10～16 mm粒径试样的1.09倍，对于圆柱体试样， 5～10 mm粒径试样的破碎分形维数是10～16 mm粒径试样破碎分形维数的1.11倍。说明混凝土破碎分形维数大小受到粗骨料粒径的影响，分形维数越小，碎块数目越少，碎块尺寸相对越大，试样破碎程度越低。除5～16 mm粒径圆柱体试样外，棱柱体试样破碎分形维数均比圆柱体试样高，对于5～10 mm和10～16 mm两种粒径试样，棱柱体破碎分形维数分别是圆柱体的1.07倍和1.08倍。表明混凝土破碎分形维数大小受到试样形状的影响，破碎程度与试样形状有关。

图2 粗骨料粒径及试样形状对混凝土破碎分形维数的影响Fig.2 Influence of coarse aggregate size and specimen shape on fractal dimension of concrete fragmentation

2.3.2 破碎分形维数与混凝土抗压强度的关系

图3给出了各试样的抗压强度，图4为混凝土破碎分形维数与试样抗压强度的关系曲线。由图3可知，圆柱体抗压强度均高于同粒径棱柱体，对于5～10 mm、5～16 mm和10～16 mm三种粒径，分别高出43.75%、57.14%和54.55%，说明混凝土的抗压强度与试样形状有关；5～10 mm粒径的抗压强度依次大于同形状5～10 mm和10～16 mm粒径的抗压强度，对于棱柱体试样和圆柱体试样，抗压强度分别依次高出14.29%、27.27%和4.55%、29.41%，表明混凝土的抗压强度与粗骨料粒径大小有关。从图4可知，除5～16 mm粒径圆柱体试样外，混凝土破碎分形维数随混凝土抗压强度的提高呈增大趋势。

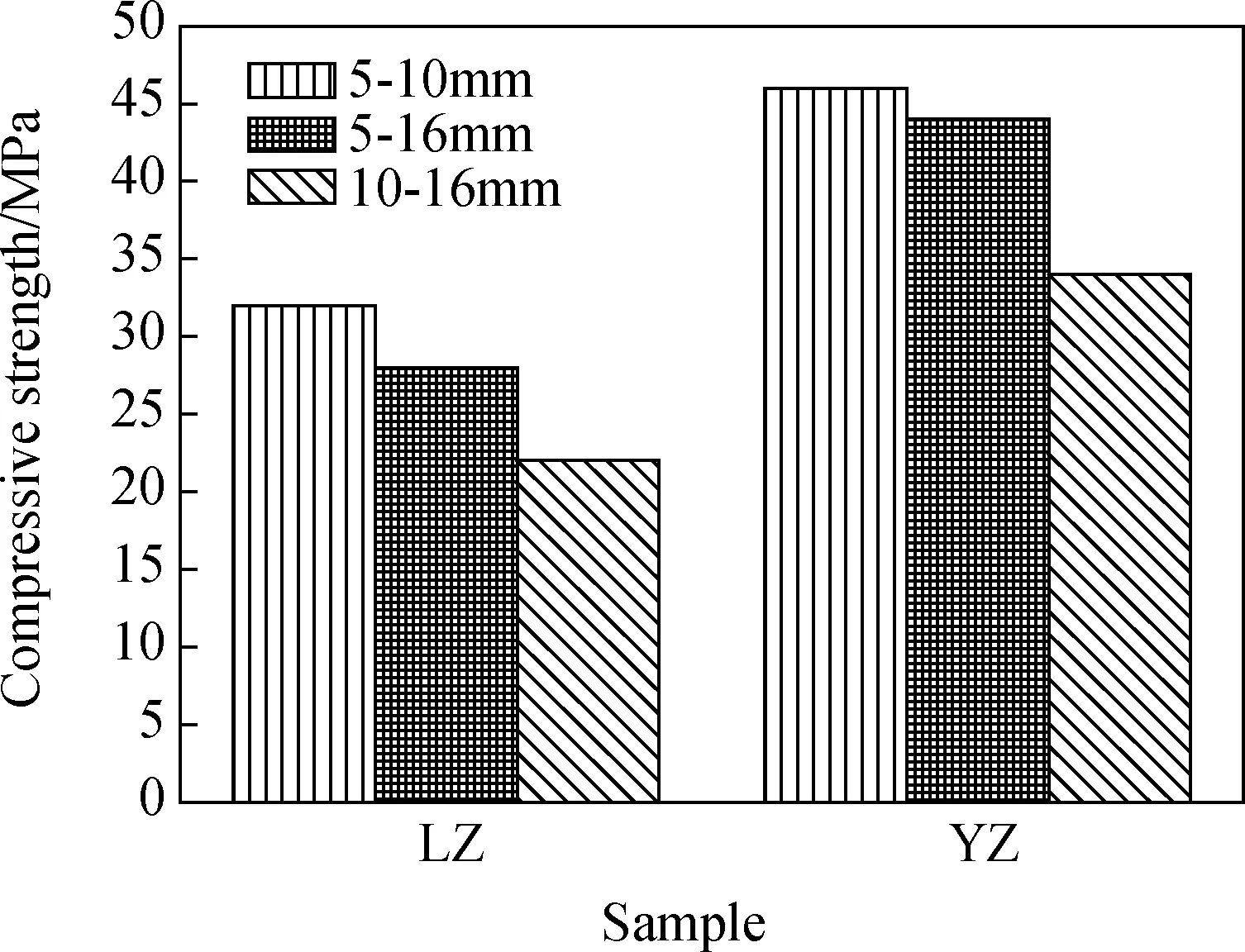
图3 混凝土抗压强度Fig.3 Compressive strength of concrete

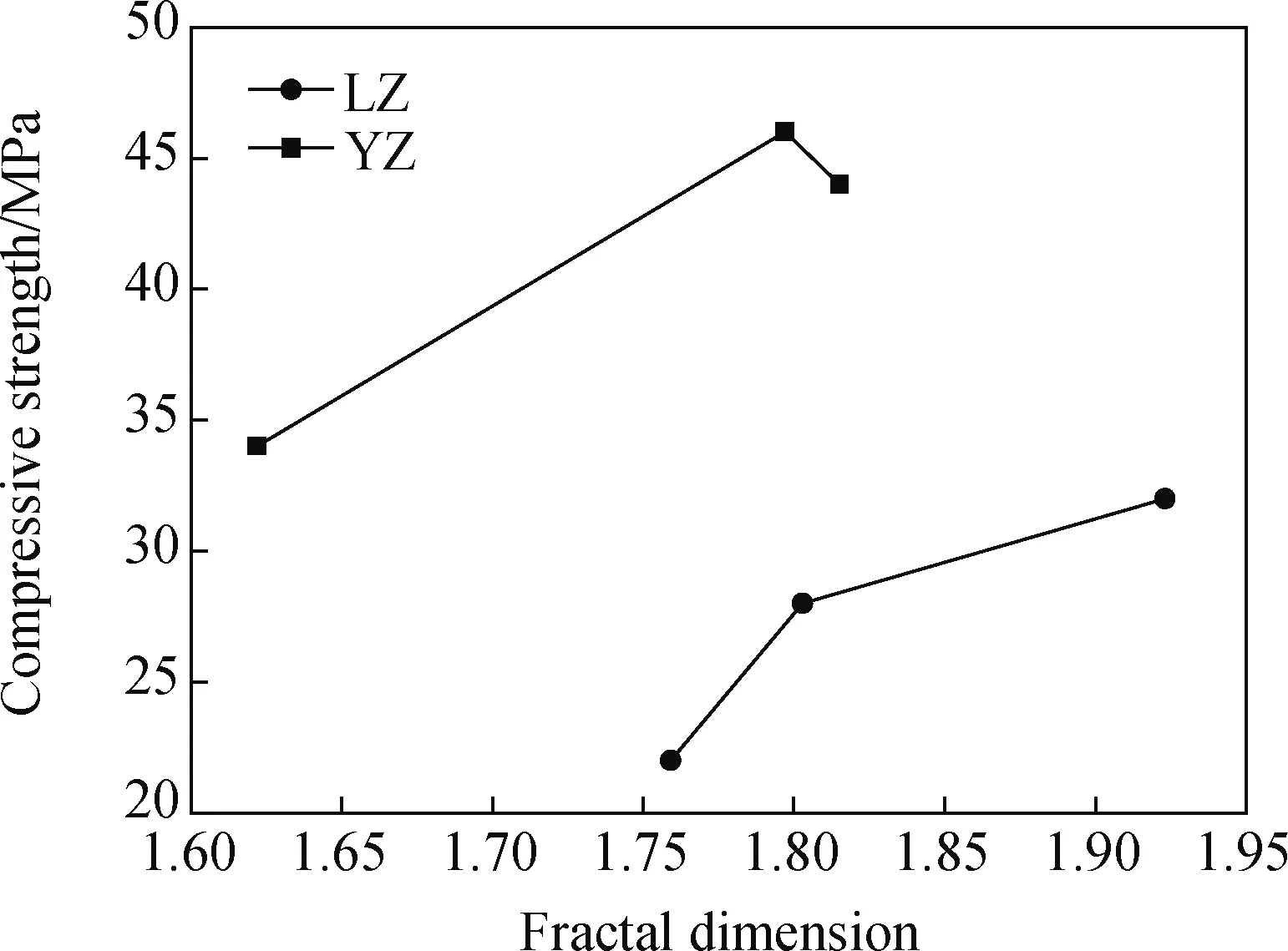
图4 混凝土破碎分形维数与抗压强度的关系Fig.4 Relation of fractal dimension of concrete fragmentation and compressive strength

2.3.3 破碎分形维数与峰值应变的关系

图5给出了各试样的混凝土破碎分形维数与峰值应变的关系。由图可知，圆柱体试样峰值应变均高于同粒径棱柱体，对于5～10 mm、5～16 mm和10～16 mm三种粒径，分别高出1.49%、43.93%和33.33%，说明混凝土的峰值应变受到试样形状影响。对于棱柱体试样，5～10 mm粒径的峰值应变依次高出5～16 mm粒径25.23%、10～16 mm粒径32.10%，对于圆柱体试样，除5～16 mm粒径外，峰值应变亦随粗骨料粒径的减小而增大。无论棱柱体试样还是圆柱体试样，混凝土破碎分形维数均随峰值应变的提高而呈增大趋势。

图5 破碎分形维数与峰值应变的关系Fig.5 Relation of fractal dimension of concrete fragmentation and peak strain

2.3.4 破碎分形维数与试样单位体积吸收能的关系

鉴于单位体积吸收能[18-19]能够反映试样的破碎程度，本文对各试样的单位体积吸收能进行了计算(具体计算方法见式(9))，并探讨了单位体积吸收能与破碎分形维数的关系。各试样的单位体积吸收能与破碎分形维数的关系见图6。

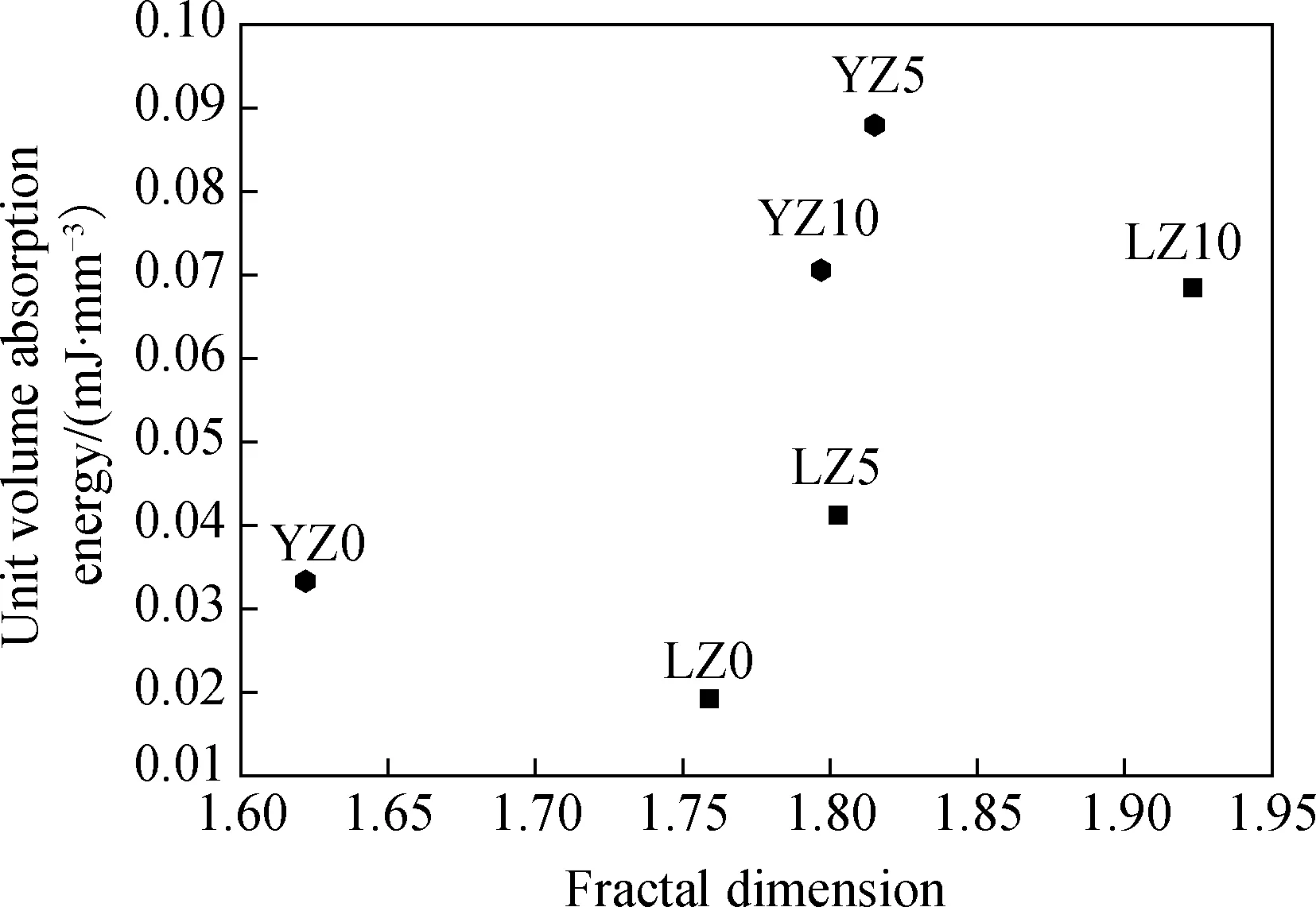
图6 各试样的分形维数与单位体积吸收能的关系Fig.6 Relation of fractal dimension and unit volume absorption energy

(9)

式中，W为试样的单位体积吸收能，F为试验力，u为试样的变形，V为试样体积。

可以看出，圆柱体试样的单位体积吸收能均比同粒径的棱柱体试样高，对于5～10 mm、5～16 mm和10～16 mm三种粒径，分别提高3.08%、113.49%、73.26%，说明混凝土单位体积吸收能与试样形状有关。对于棱柱体试样，5～10 mm粒径的单位体积吸收能依次比5～16 mm、10～16 mm粒径的高出66.16%、26.77%，对于圆柱体试样，除5～16 mm粒径外，单位体积吸收能同样随粗骨料粒径的减小而增大。且不论棱柱体试样还是圆柱体试样，混凝土破碎分形维数均随单位体积吸收能的增加而呈增大趋势，表明混凝土试样的单位体积吸收能越多，破碎分形维数越大，破碎程度越高。这是因为单位体积吸收能越大，混凝土试样在破坏过程中的能量耗散及能量释放相应就越大，导致形成的微裂纹也就越多，产生的破裂面也就越多，出现更多尺度的碎块也就越多，破碎就越严重[20]。

2.3.5 破碎分形维数与混凝土脆性指标的关系

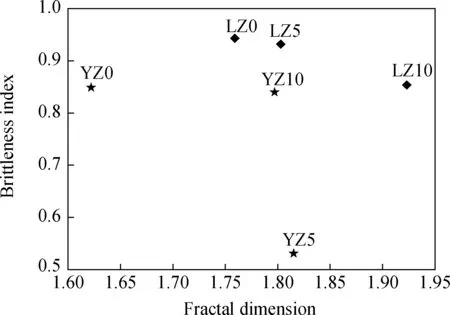
图7 各试样的破碎分形维数与脆性指标的关系Fig.7 Relations between fractal dimension and brittleness index

B7=(σp-σr)/σp

(10)

式中，B7为脆性指标，σp为峰值强度，σr为残余强度。

可见，棱柱体试样的脆性指标均高于同粒径的圆柱体试样，对于5～10 mm、5～16 mm和10～16 mm三种粒径，分别高出2.3%、75.5%、11.11%，说明试样形状对脆性指标有影响；对于棱柱体试样，5～10 mm粒径的脆性指标依次低于5～16 mm粒径8.44%、10～16 mm粒径1.2%，对于圆柱体试样，除5～16 mm粒径外，脆性指标依然随粗骨料粒径的减小而降低。两种形状试样的破碎分形维数均随脆性指标的降低而呈增大趋势，说明脆性指标越小，破碎分形维数越大，破碎程度越高。

3 结 论

基于Turcotte研究理论，通过混凝土单轴压缩试验，对混凝土破碎后的分形特征进行了研究。分析了粗骨料粒径和试样形状对混凝土破碎分形维数的影响，讨论了抗压强度、峰值应变、单位体积吸收能、脆性指标与破碎分形维数的关系，得出以下结论：

(1)混凝土单轴压缩破坏后的碎块分布具有分形特征。

(2)棱柱体试样的破碎分形维数随粗骨料粒径的增大而降低，随混凝土抗压强度的提高而增大。

(3)圆柱体试样的破碎分形维数除5～16 mm粒径外，随粗骨料粒径的增大亦呈降低趋势，随混凝土抗压强度的提高呈增大趋势，与同粒径的棱柱体试样相比呈降低趋势。

(4)两种形状试样的破碎分形维数均随峰值应变的提高、单位体积吸收能的增加、脆性指标的减小而增大。