关于全球气候变化和极端天气数据的量化分析

陈 波 姬家昌 多俊杰

（1、大连民族大学经济管理学院，辽宁 大连116600 2、大连民族大学计算机学院，辽宁 大连116600）

1 概述

温室效应不断积累导致全球变暖。罪魁祸首就是二氧化碳，即温室气体，温室气体对地球的长波辐射具有较强的吸收性，并且对于太阳光有高度透光性，于是产生了温室效应[1]。由于温室效应的存在，导致地球与大气之间的吸热和放热系统失衡，造成全球气候变暖[2]。科学家认为全球气候变暖势必对于地球生物包括人类带来灭顶之灾。而实证数据发现，21 世纪以来，全球全年平均气温在10 年间上升率仅为0.03℃，相对于如此长的时间跨度来说几乎未变化，这种现象被科学家叫作Hiatus（全球变暖停滞状态）[3]。这也使得全球气候变暖这一话题备受争议。尤其是部分地区出现了“极寒天气现象”，使得更多人怀疑是否真的存在“全球气候变暖”。

2 时间序列模型模型建立

2.1 连续复小波变换模型

鉴于考虑的是某一地区的温度在时空变化上的趋势，所以优先考虑选择时间序列模型，时间序列基本含义是指把经过处理的统一指标的数值按照时间先后发生的顺序进行排列。其可划分为四部分：长期趋势（trend）；季节变动（seasonal）；循环变动（cycling）；随机波动（irregular）。

长期趋势（T）：长期受一些基本因素影响的现象及变化趋势的形成。

季节变动（S）：有规律的周期性变化的现象，在一年的季节变化。

循环变动（C）：这种现象的波动形式在几年内的规律性波动。

不规则变动（I）：它是一种不规则变化，包括严格的随机变化和影响很大的不规则突变。所以采取该模型能够不仅能够分析加拿大地区温度长期趋势。

自相关系数值是测量不同时间点上的观测值相互之间的相关程度。它是一个概率模型，其作用是用来洞悉产生数据的。自相关图是用来解释自相关系数集合的工具。有两种，自相关函数和偏自相关函数。使用自相关程序可以绘制出自相关函数图以及偏自相关函数图。自相关过程只使用于时间序列数据。

①样本相关系数的计算方法是

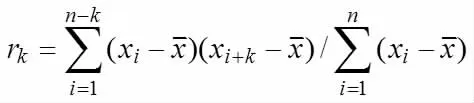
②时间序列含有缺失值情况的情形

如果X 存在缺失值，则计算的统计量是不同的。首先，给其一个定义：

x=非缺失值X1，…. Xn 的平均值

对于K=0，1，2，……以及J=1，2，3，….n 有

其中，mk=在，…….b中非缺失值的数量；m0=在x 中非缺失值的数量。

通过对数据的处理，制作出自相关性的分析可以从图中直观的看出。

2.2 模型建立以及解释

表1 模型统计表

由表可知，拟合优度达到0.938，比较模型的平稳部分和平均模型。当有趋势或者季节模式时，本测度比普通R 方更好。平稳的R 方取值范围为负无穷到1，R 方为负无穷到0 表示模型比基准模型更差，0 到1 表示在考虑中模型比基准模型更好。本次模型中R 方为0.938 为正值，其趋近于1，表明在考虑中模型比基准模型更好。建立时间序列模型后对数据进行了预测，并将预测的数据和实际数据做成序列图，可以看出预测的温度与真实的温度非常贴合，真实温度在高峰中普遍稍高于预测温度更高，低锋更低。整体上预测和区间还有趋势比较符合真实的温度，可以得出该模型建立能较好的符合真实的情况。在建立的各地模型之后并对未来一年的温度并进行了预测，预测结果如图1 实测与预测序列图所示。

选取加拿大几个典型地区为例，如图2 是加拿大的埃德蒙顿、雷吉那、温尼伯和维多利亚四个城市的时间序列和预测的未来一年的模型，可以看出虽然在空间上的不同，但是各地随着年份的增加温度的最低点、最高点和整体温度都呈现小幅的上升的趋势，并在未来可能持续的缓慢的增长。

3 基于Morlet 复小波变换时间序列分析

3.1 模型原理

1980 年，Morlet 提出了一种新的方法，时频多分辨率小波分析方法。这种方法使得更好地研究时间序列问题成为可能，它可以非常清晰地揭示出时间序列中隐藏的各种变化周期，充分反映出在不同时间尺度下系统的变化趋势，这对用于未来系统的开发有着重大的意义，并能对发展趋势进行了定性估计。

图1 实测与预测序列图

图2 各地时间序列预测图

3.2 数据处理与模型建立

因为加拿大海洋表面温度具有"多时间尺度"的变化特征，且这种变化是连续的，因此应采用连续小波变换进行分析。另外，实小波变换仅仅显示出时间序列变化的幅度和正负性，然而，复小波变换可以同时给出两方面信息，其中包括时间序列变化的位相和振幅。对问题的进一步分析非常有利。利用MATLAB 绘制了小波系数图、小波平方差图和主周期变化趋势图，然后根据上述三幅图的变化，确定了加拿大海洋表面温度时间序列中存在的多时间尺度规律。由于本例中的海洋表面温度数据是有限时间数据序列，因此往往可能在时间序列的两端生成“边界效用”。为了减少误差，消除或减少序列数据的边界效应，需要对两端的数据进行扩展。完成小波变换后，去除两端扩展数据的小变换系数，保留原始数据序列的小波系数。在本例中，我们使用matlab2018b 小波工具箱中的信号扩展函数对称地扩展数据。

3.3 模型结论

根据小波方差检验的结果与分析如图3 所示，我们绘制出了海洋表平面温度的第一到第三周期的小波系数图。

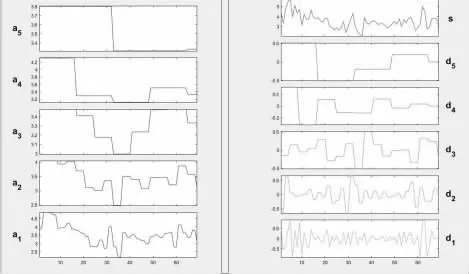
图3 小波模型分析图

从图中分析出在不同的时间尺度下，海洋表面温度在温度升高和降低的变化上存在周期性波动的特征，在1950～1981 年之间，大约经历了8 个周期，每个周期3.86 年左右；而在1982～2018年的36 年间经历6 个周期，每个周期6 年左右。