一道定积分计算题的拓展应用

覃桂茳 覃学文 石向东

0 引言

《高等数学》是大学生为将来学习与工作的基础学科，是专业知识课程的桥梁，体现专业学生的职业素养。开展《高等数学》教学活动的目的是通过本课程的学习，使学生理解和掌握微积分的基本概念、理论和方法，培养学生具有熟练的基本运算能力，为后续课程奠定必要的数学基础。

本文结合自身的教育工作经验，以一道定积分的计算题作为案例分析，通过案例的拓展和延伸，提高学者们的计算能力。

1 案例分析

本文以文献[1]中（教材第175 页）的例1 作为案例进行分析。

解：设 x=asint，则 dx=acostdt，且当 x=0 时，t=0；当 x=a 时于是，

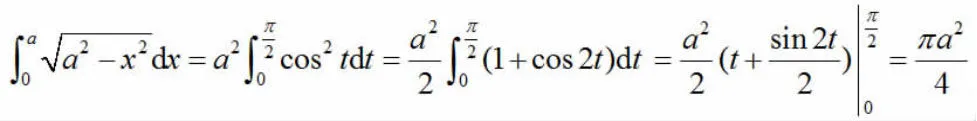
2 拓展与应用

为了提高学者对定积分计算知识的掌握，利用定积分的运算法则和性质，结合函数的四个性质（奇偶性、周期性、单调性、有界性）以及换元法，对例1 进行拓展与应用。

2.1 利用定积分的几何意义求定积分

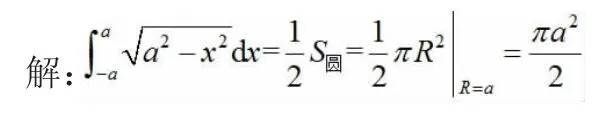
2.2 在对称区间下利用函数的奇偶性求定积分

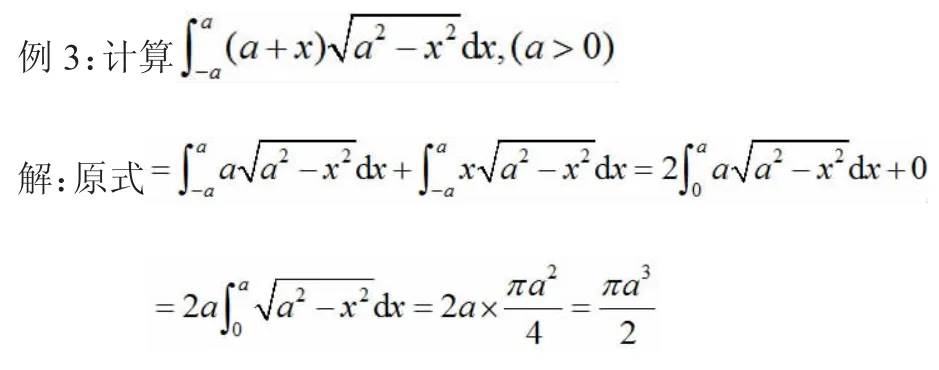
2.3 利用函数的周期性求定积分

引理[2]：

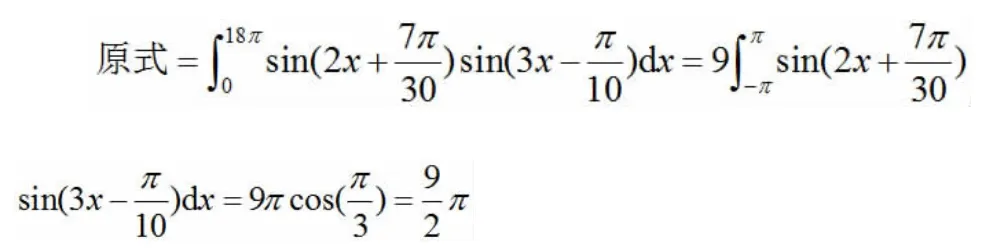
2.4 利用函数的单调性求定积分

若f（x）在[a，b]上连续的单调函数时，则：

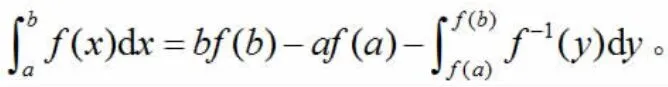
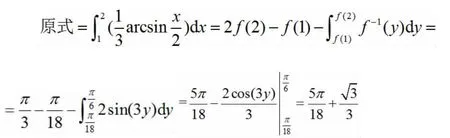
注：满足以下两个条件，可由对x 轴积分转化为对y 轴积分：f（x）的反函数容易找出；相对更容易计算。

2.5 利用函数的有界性求定积分

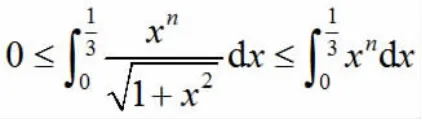
利用定积分的中值定理，有：

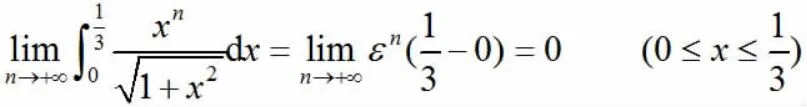
利用由极限的夹逼定理，可得：

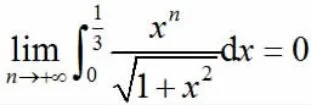
2.6 利用换元法求定积分

计算定积分时，首先观察被积分函数，然后观察上限和下限。不能立即得到被积分函数的原函数，则不能直接使用牛顿—莱布尼茨公式，就应该考虑被积分函数是否具有上述的四种性质，然后按照相应的解法计算定积分。比如，像这道证明题无法从定积分的被积分函数找出解题思路，则需要考虑换元法求解问题。

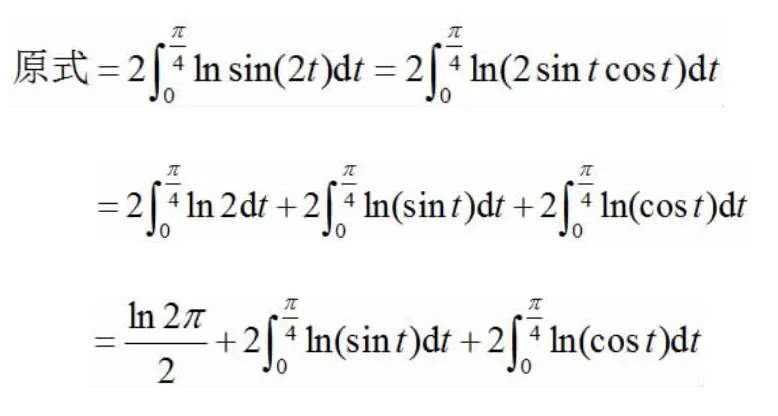
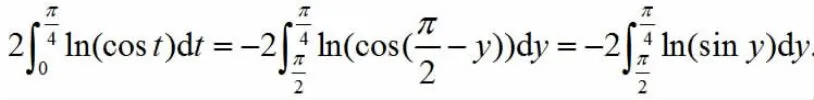
代入原式，并利用定积分的可加性，得：

3 小结

通过上面的例子可以看到，使用单一的方法是不能计算较复杂定积分，需要多种方法和技巧的结合方可解决问题。培养学生分析问题能力，提高学生的计算能力等综合能力，一直是教育工作者追求的目标。