2:1 内共振条件下变转速预变形叶片的非线性动力学响应1)
顾 伟 张 博 丁 虎 陈立群
(上海大学力学与工程科学学院,上海 200444)
(长安大学理学院,西安 710064)
(上海大学上海市应用数学和力学研究所,上海 200444)
(上海大学上海市能源工程力学重点实验室,上海 200444)
引言
在实际工程结构中,叶片是最重要的传动部件之一,如在涡轮机叶片、船用螺旋桨、直升机叶片以及风力发电装置中都有广泛应用.近年来,随着人们对机械性能要求的提高,叶片的工作环境更加严峻,常需在复杂工况下(如高温、摩擦等)切换转速,极易使叶片产生变形,导致发生破坏,因此研究预变形变转速叶片的动力学特性对于合理设计叶片结构具有重要意义.
由于机械工程上的大量应用,旋转叶片的动力学特性长期以来都是国内外学者关注的重点,许多学者采用理论分析,数值模拟以及实验方法针对不同叶片模型,在线性或非线性框架下,研究了常转速下旋转叶片的动力学响应规律.前期,一些学者[1-2]研究了在常转速下,考虑旋转叶片模型的建立问题,得出其动力学方程,通过不同方法求解其自由振动等问题.Yoo 等[3-5]通过混合坐标系建模研究了常转速下预扭悬臂梁受不同外激励下的振动特性.蔡国平和洪嘉振[6]通过变结构控制法对匀速转动悬臂梁进行主动控制,并且比较零次近似模型和一次近似模型的巨大差异.Yang 等[7]利用广义哈密顿原理推导了常转速下Euler-Bernoulli 梁横向振动的非线性微分方程.姜静和韩广才[8]研究了常转速叶片在弯扭耦合下由于质量偏心的动力学分析.Inoue 等[9]研究了实际问题中定转速旋转的风力发电机受重力和风力影响的振动特性.Ramakrishnan 和Feeny[10]进一步在模型建立过程中加入非线性项来研究其动力学特性,随后Ramakrishnan 和Feeny[11]建立了强迫马蒂厄方程来考虑风力叶片的共振,李国强等[12]通过风洞试验研究翼型横摆震荡.赵国威和吴志刚[13]在文献[6]的基础上进一步用一次近似模型考虑将轴向和横向变形产生的耦合项代入应变能中,考虑其对动力学特性的影响.杨鄂川等[14]研究了常转速下,叶片受开口裂纹作用下的振动特性,观察梁的一阶、二阶固有频率随不同裂纹深度和位置的变化.Oh 和Yoo[15]考虑了拉伸、弯曲和扭转的耦合作用下,常转速预扭转叶片的振动分析.Tian 等[16]提出一种改进的变分方法,推导了旋转梁的自由和瞬态振动特性.李炳强等[17]研究了在常转速下,转子--叶片耦合系统在主共振条件下的振动响应和动态稳定性.吴吉等[18]基于绝对节点坐标法研究悬臂曲梁的纯弯曲问题和带有刚柔耦合的旋转柔性非线性动力学响应问题.
由于转子圆盘叶片系统经常会受外部扰动,考虑转速随时间变化更加普遍也更贴近实际.例如当发动机启动、变速、停机等过程中,转子的输入与输出功率(扭矩)失衡.转子在转动过程中将伴随扭振,从而产生了速度脉动,使得叶片转速不再是一个常数.近年来,有越来越多的学者将目光转移到变转速叶片的动力学行为的研究中.Kammer 和Schlack[19]首先将角速度表示为稳态值和微小扰动的叠加,探究变转速对梁振动的影响.Young[20]研究了变转速下,预扭转变截面梁的动态响应,利用多尺度法处理方程,并研究阻尼系数对不稳定区域的影响.Yang 和Tsao[21]研究了非定常转速下,预扭转叶片振动与稳定性分析.张伟等[22]针对1/2 亚谐共振和1:3 内共振,通过数值模拟得到二维、三维相图,分析了风速变化对变转速叶片振动的影响.Yao 等[23]考虑了在高温超声波气流变转速叶片的动力学响应.随后,Yao 等[24]研究了叶片在不同转速下的非线性振动和稳态响应.Georgiades[25]研究了在非定常转速弹性连续体中传动轴动力学行为.张伟等[26]建立了变截面叶片模型,分析在变转速下叶片受气动力和离心力影响的非线性动力学行为.Hu 等[27]提出一种新型的三维预扭梁单元公式来捕捉变转速梁高度耦合的振动特性.
近期,有学者报道了叶片结构的预变形将严重影响叶片的动力学响应.Zhang 和Li[28]研究了在常转速下,预扭转叶片在2:1 内共振下的受迫振动.Kang 等[29]基于载荷增量法,提出一种新的预变形方法来补偿叶片变形,通过修正刚度矩阵考虑非线性叶片刚度的影响.Zhang 等[30]研究在2:1 内共振下旋转预扭转梁的主共振情况,详细研究了不同参数变化对幅频响应曲线的影响.
通过文献调研发现,较多文献考虑变转速情况时往往不考虑预变形作用,而文献[28]主要考虑常转速下预变形叶片受外激励作用.同时考虑变转速和预变形两种因素共同作用下的叶片动力学行为相关的研究还尚未见报道.本文主要研究变转速预变形叶片在2:1 内共振下受参数激励的响应并考虑立方非线性项对系统的影响.
1 动力学方程
如图1 所示为一长度为L的变转速预变形细长叶片.其一端固结在转轴半径为r的圆盘上,另一端自由,考虑叶片转速由一定常转速Ω1和一简谐变化的微小扰动Ω2sin(!t)叠加而成,即Ω(t)=Ω1+Ω2sin(!t).叶片在安装时与圆盘有一定的角度,称为安装角Ψ.叶片的总预扭角为Θ.由于受温度梯度影响,叶片产生预变形u20和u30,分别表示弦向和翼向,忽略轴向预变形(轴向预变形远小于其他两个方向),利用旋转坐标可得到在热梯度作用下预扭叶片沿截面两主轴的曲率函数,见文献[28].为了描述叶片振动过程中的构形,本文建立了两套坐标系,一套惯性坐标系XYZ固定在圆盘中心,一套旋转坐标系xyz连接在旋转叶片根部上,x沿着未变形叶片的轴线方向(左右),y为弦向(前后),z为翼向(上下).

图1 变转速预变形叶片示意图Fig.1 Diagram of pre-deformed blade with varying speed
为了推导出叶片的解析模型,本文作出如文献[5,28]中假设,根据Von-Karman 应变--位移公式
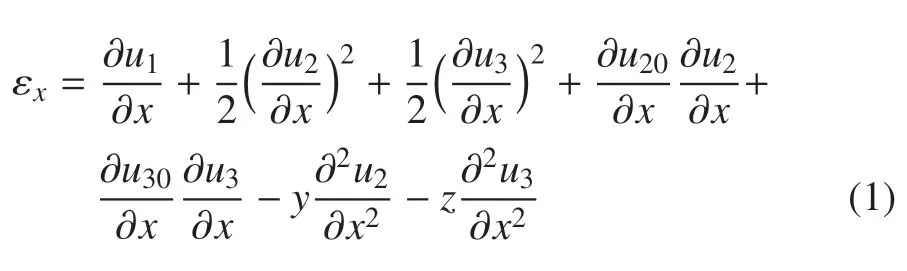
上式中,u1,u2,u3表示为梁轴线上任一点处位移,通过上述假设,变形能可写成如下形式
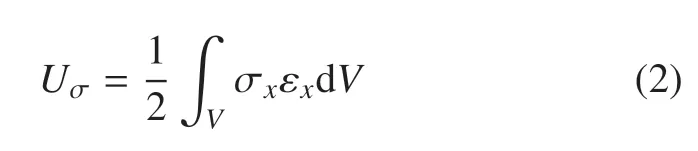
由于离心力作用产生的轴向收缩势能可表达为
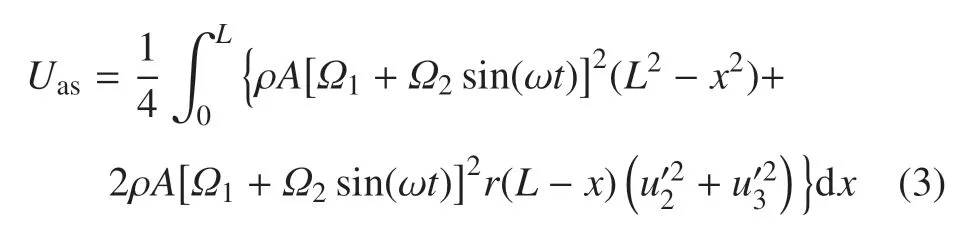
可得总势能为

旋转叶片的动能可表达如下

其中,顶标 表示对时间求微分,在此文中对于外力做功,只考虑黏性阻尼力的作用,阻尼系数为cd.
利用假设模态法,将位移函数分解成关于时间和空间的函数,空间函数表达如下

上式中参数βj,可见文献[31].
将式(4)和式(5)代入Lagrange 动力学方程中,为了使方程更具普遍性,引入无量纲参数,如下
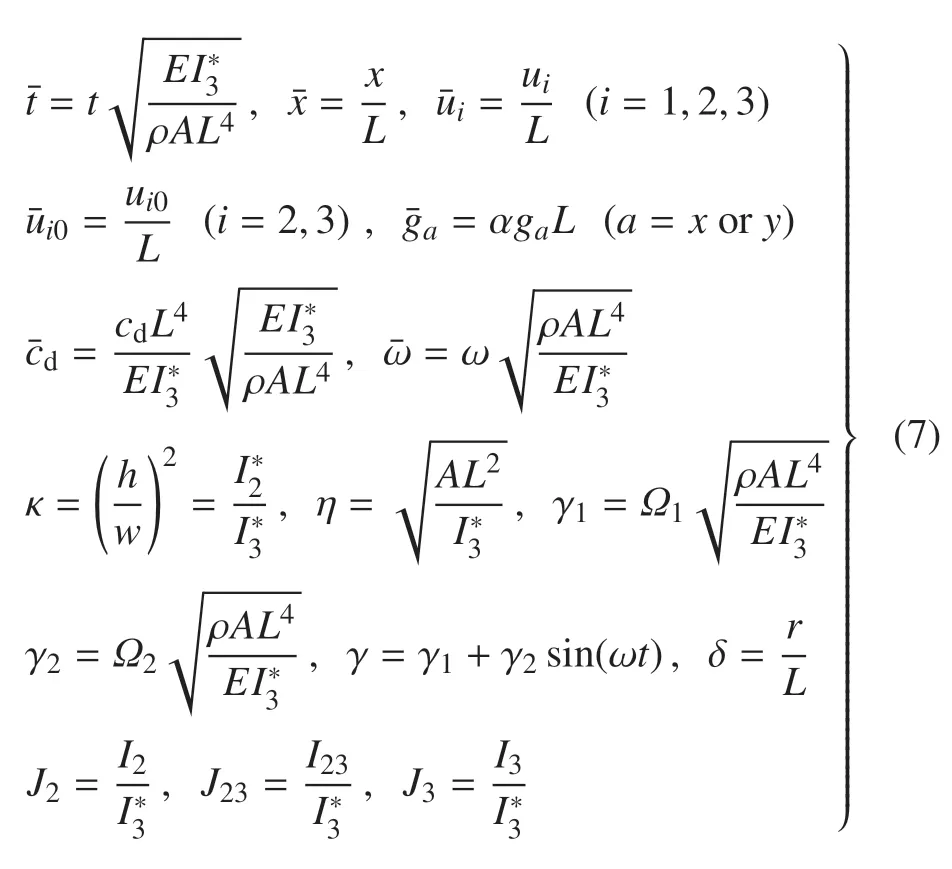
对方程进行处理,为了书写的简洁性,将式(7)中无量纲参数中上划线符号忽略不写,可得下列无量纲化动力学方程




上式方程中下划线代表与文献[28]一文中受迫振动不同项,方程(8)控制着轴向运动,方程(9)、方程(10)控制着弦向和翼向,从上式中可以发现加上预变形,方程中多了平方项和立方项,令预变形项为零、转速变为常转速并且不考虑外力项,方程就退化成文献[5]的模型.
2 多尺度分析
正如文献[5]中所说,对于细长欧拉梁,其轴向第一阶固有频率远高于弯曲振动固有频率,叶片系统前几阶模态主要表现为弯曲变形,因此忽略轴向收缩变形与弯曲变形耦合作用,上式只留下方程(9)和(10),同时将方程中双下划线部分(跟q1j相关项)略去,并通过模态矩阵[30]对线性部分进行解耦,可得下式
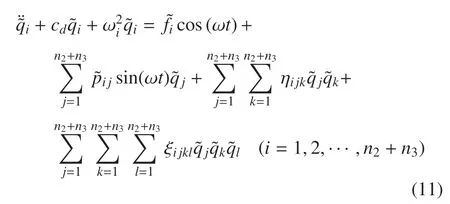
上式方程中各系数可见附录,ηijk,ξijk参数可见文献[32]对方程(11)进行重刻度

并将非线性方程稳态解展开成下式
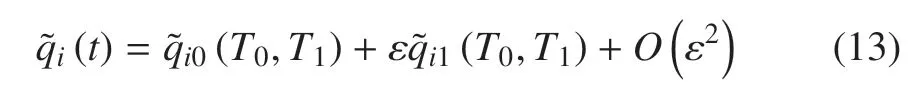
其中,T0=t为快时间尺度,T1=为慢时间尺度,将方程(13)代入方程(11)中,分别取阶可得

从方程(14)中可求得
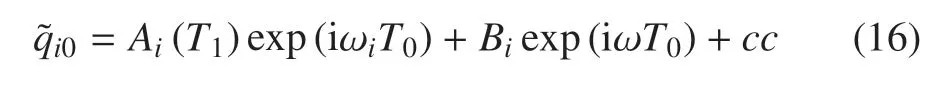
其中,Ai是关于T1的复函数,cc表示前面各项的复共轭项.Ai和Bi表达式如下
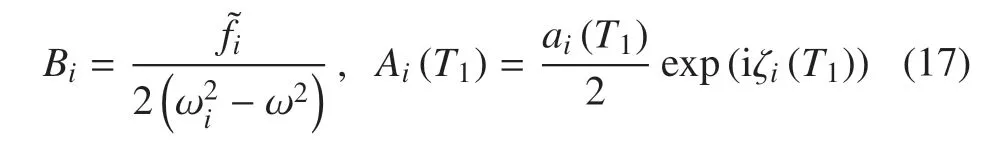
其中,ai和ζi分别为幅值和相角,均为慢时间尺度T1的函数,将式(16)代入式(15)中,可得

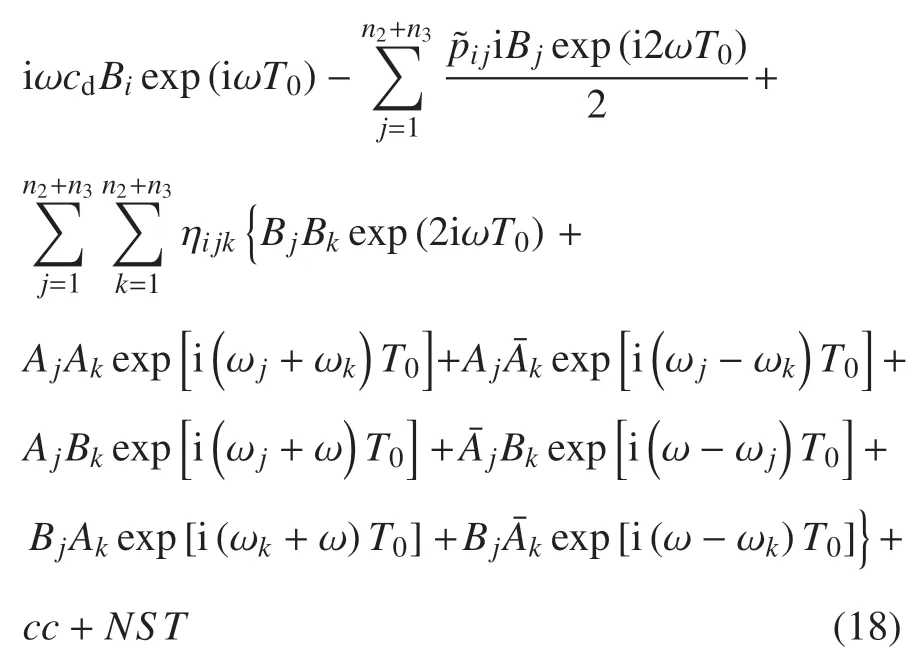
文献[28]的图3 和图4 详细研究了旋转预变形叶片随转速、预变形程度变化过程中,系统前两阶固有频率的变化规律.发现在特定的组合参数下,系统具有发生2:1 内共振的可能性.为研究2:1 内共振下,非线性振动系统发生一阶次谐波共振的振动特性,引入两个解谐参数σ1和σ2,用σ1表示接近的程度,用σ2表示接近的程度

从方程(18)中消除久期项,分离实部和虚部可得如下的演化方程

其中,上标I 表示虚部,R 表示实部
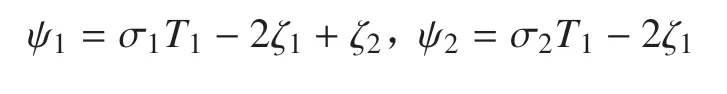

当a1,a2,与时间T1无关时,可以求解得到系统的稳态响应.因此方程(20)可令等式左边为零,并求解对应的非线性代数方程组即得到系统的稳态响应,解分为两种情况:(i)a1=0,a2≠0 称为单模态解;(ii)a1≠0,a2≠0 称为双模态解,系统的稳定性可以通过Lyapunov 准则判断,具体可见文献[32-33].
4 参数变化对系统频响曲线的影响
图2~图4 分别考虑了温度梯度、阻尼系数以及转速扰动幅值对模态频率响应的影响,图中实线表示稳定区域,虚线表示不稳定区域,由上述图可以得知在2:1 内共振中,模态频率响应曲线中会同时出现软特性和硬特性.由图2 可知,随着温度梯度的增大,一阶、二阶模态频率响应曲线有向外张开的趋势且峰值增大,其不稳定区域变大;在图3 中,随着阻尼系数的增大,曲线仍有向外张开的趋势,但峰值降低,表明当有阻尼约束时,对系统振动有较大的抑制作用,由图3 可见,阻尼系数由0.1 变为0.3,响应峰值降低近3 倍,同时不稳定区域变小;在图4 中,随着扰动转速的增大,曲线呈现出向内闭合的趋势且峰值增大,并且不同于温度梯度影响,在不同扰动转速在同一频率下,其幅值不会相交.
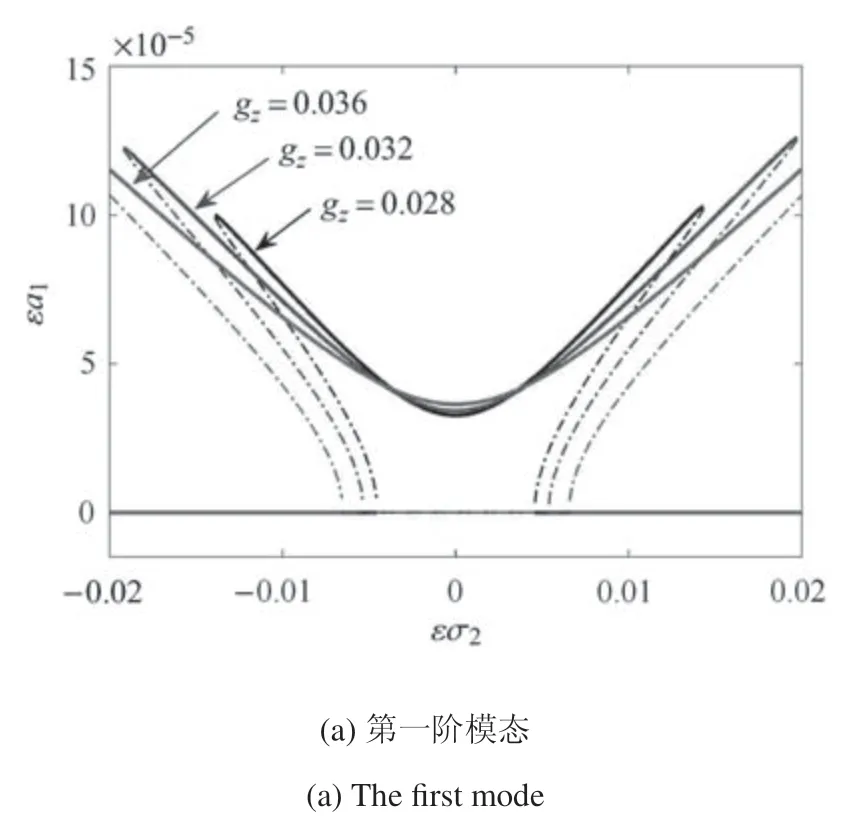
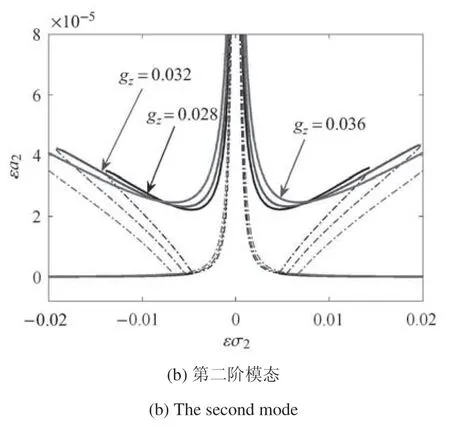
图2 温度梯度变化对前两阶模态频率响应曲线的影响Fig.2 The effect of temperature gradient on the responses of the first two modal frequency
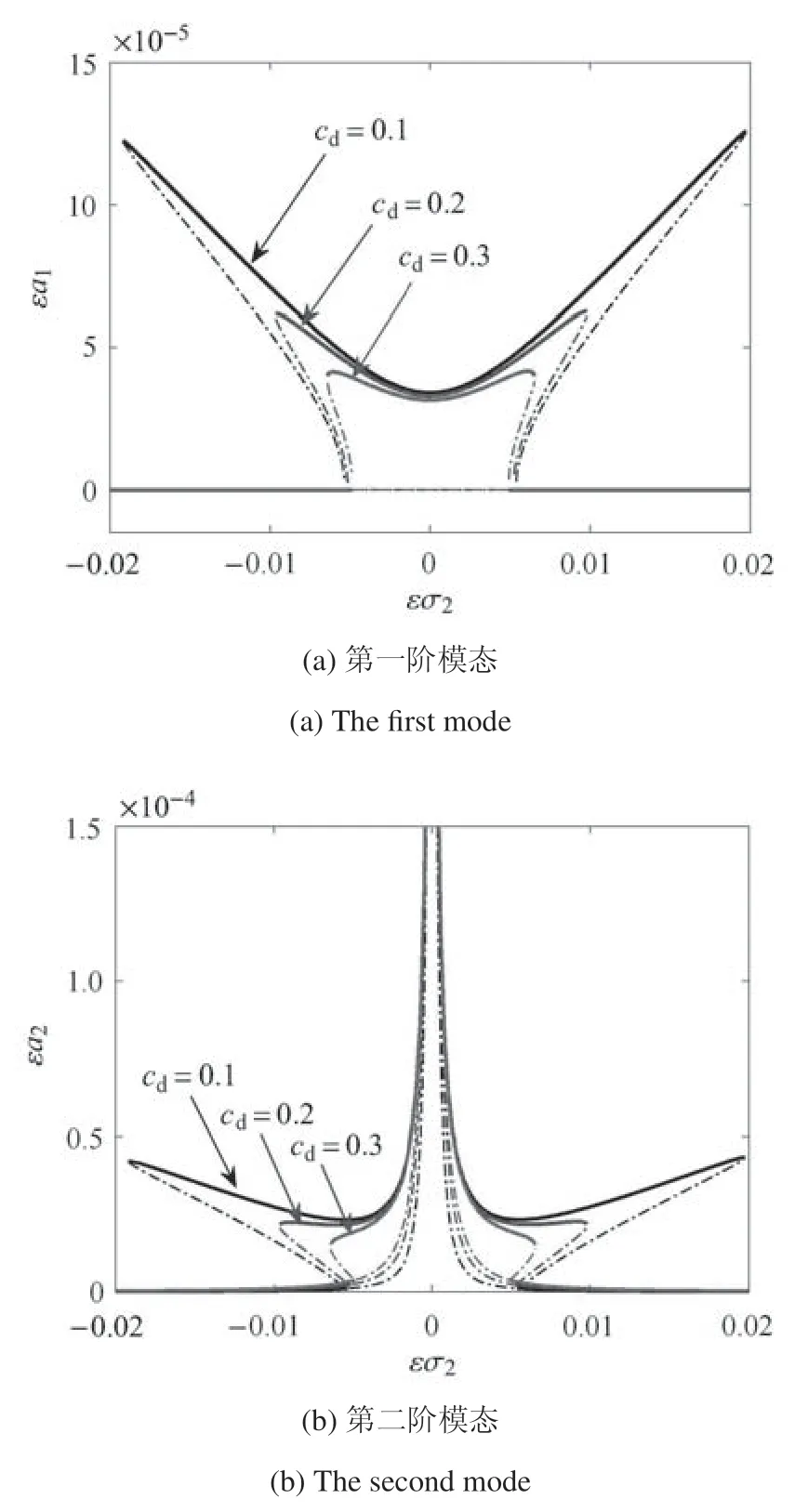
图3 阻尼变化对前两阶模态频率响应曲线的影响Fig.3 The effect of damping on the responses of the first two modal frequency
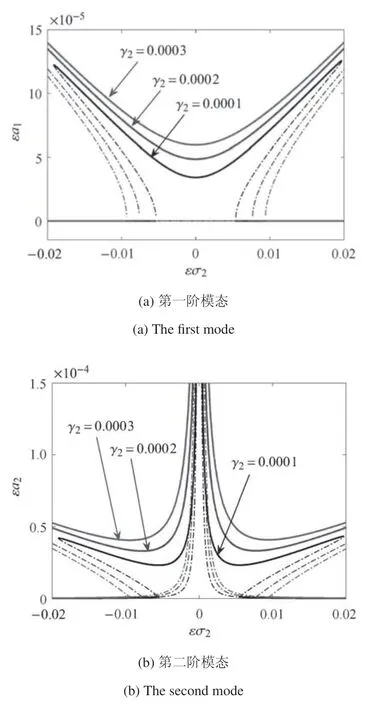
图4 转速扰动幅值变化对前两阶模态频率响应曲线的影响Fig.4 The effect of amplitude of revolution disturbance on the responses of the first two modal frequency
5 数值验证
为了验证本文建模的正确性,忽略本文建立的动力学模型中预变形和转速的影响,将本文模型得到的前四阶固有频率与其他文献进行了对比,如表1 表示.
表1 中与文献[5,34]进行了比较,发现前四阶固有频率最大误差不超过0.1%.
为了验证多尺度法得到的系统稳态解的正确性,本节采用Runge-Kutta 法对系统动力学方程(11)进行数值积分.在数值积分中,仿真时间设定足够长,以确保系统处于稳态响应,同时,数值积分初值在单模态稳定解附近选取.

表1 前四阶固有频率的比较(γ=0,κ=0:25,δ=2)Table 1 Comparison of the lowest four natural frequencies(γ=0,κ=0:25,δ=2)
通过正向、反向扫频研究立方项在2:1 内共振中对方程的影响程度,结果如下.
图5 中圆圈代表对原系统数值积分中不考虑立方非线性项影响,加号代表考虑立方非线性项,实线代表解析解,红色虚线代表不稳定区域.可以发现在2:1 内共振下,立方非线性对系统响应影响很小,仅在完全内共振处有细微偏差.同时,在正向和反向扫频中,发现有两处跳跃点,在频响曲线的多解频带中,系统有两个渐进稳定解和一个不稳定解,由于在实验中只能实现渐进稳定运动,因此在正反两个方向扫频激励中会出现图示路径的跳跃现象,并且跳跃点附近双模态解吸引域较小,稳态解吸引到单模态解中,振幅发生突变.解析解和数值解吻合较好,从侧面证明多尺度处理的正确性.
此外,利用控制变量的思想,探究了扰动速度γ2和解谐参数σ2的改变对系统动力响应的影响.
图6 中,当固定σ2=0:8 时(图6(a),图6(b),图6(c)),随着γ2的增大,系统经历了单周期拟周期单周期的变化历程.类似的,当固定γ2=0:000 9 时(图6(d),图6(b),图6(e),图6(f)),系统经历了单周期拟周期单周期多周期的变化历程.可以看出系统动力学行为与σ2,γ2紧密相关,随参数的细微变化,系统动力学响应会出现分岔等现象.
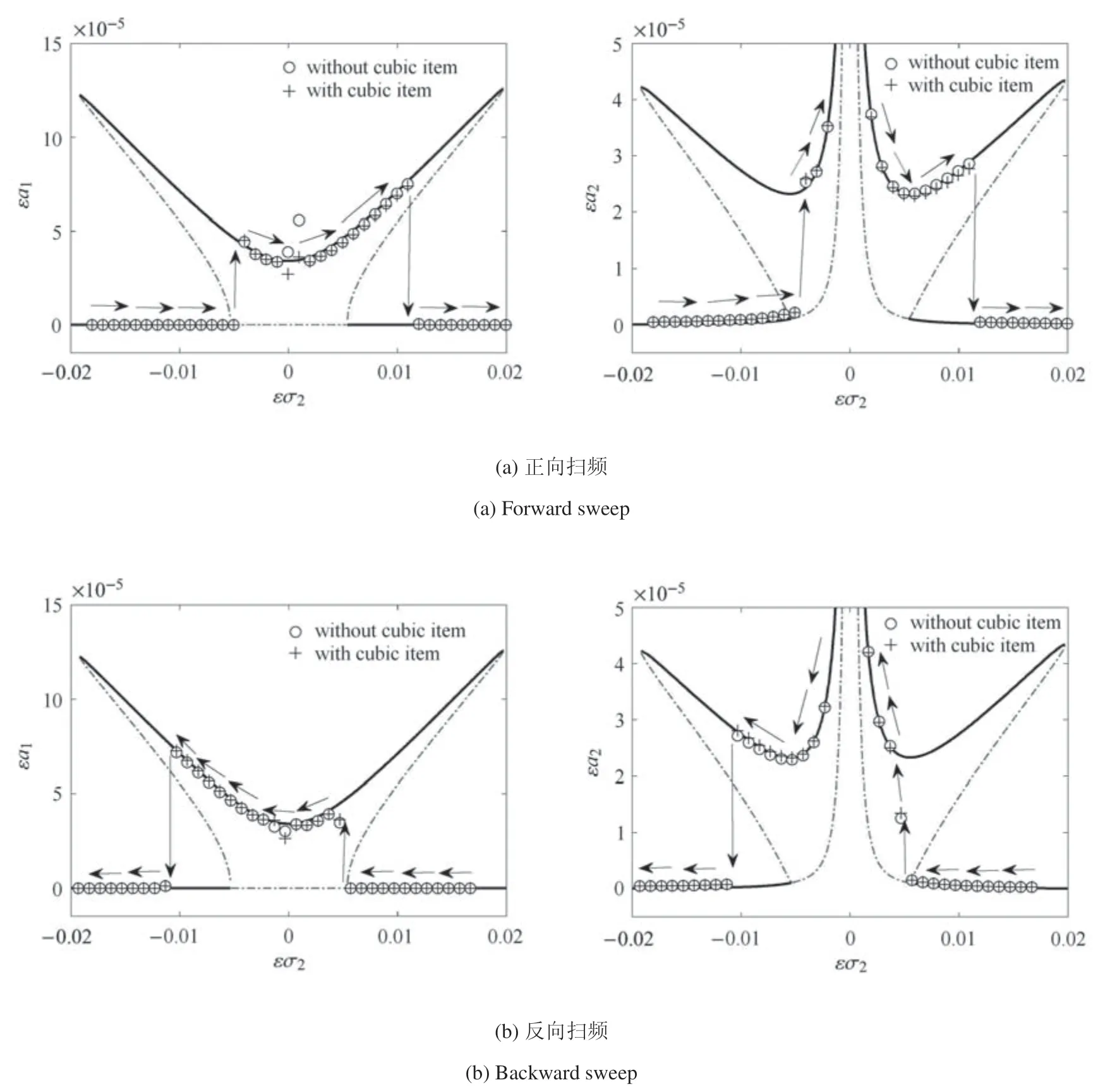
图5 正反向扫频激励数值仿真与解析解的对比Fig.5 Comparison of numerical simulation and analytical solution with forward sweep and backward sweep

图6 不同γ2 和σ2 时系统的相图Fig.6 The phase diagrams of system for different γ2 and σ2

图6 不同γ2 和σ2 时系统的相图(续)Fig.6 The phase diagrams of system for different γ2 and σ2 (continued)

图6 不同γ2 和σ2 时系统的相图(续)Fig.6 The phase diagrams of system for different γ2 and σ2 (continued)
6 结论
本文主要研究了参数激励下,预变形变转速叶片的非线性动力学特性,研究不同参数变化对系统模态频率响应的影响,并考虑立方项在2:1 内共振时对方程的影响,最后利用数值积分与解析解进行验证.结果发现:随着温度梯度增大时,模态频率响应曲线有向外张开的趋势,同时幅值增大,不稳定区域增大;当转速扰动幅值增大时,幅值同样增大,不稳定区域增大,不同于温度梯度,其模态频率响应曲线向内闭合,并且不同扰动转速在同一固有频率下,其幅值不会相交;阻尼系数改变对系统的幅值影响最大,当阻尼系数由0.1 变为0.3,其幅值降低近3 倍,同时,不稳定区域减小;立方项在2:1 内共振中对方程的影响可近似忽略,利用原系统数值积分对解析解进行验证,发现两者吻合较好.
附录A
式(11)中各矩阵及其表达式如下