孔隙率各向异性下饱和多孔弹性地基动力响应1)

熊春宝 胡倩倩 郭 颖

(天津大学建筑工程学院,天津 300072)

引言

温度、渗流及应力场等多场耦合问题在地热资源开发、核废料处理以及垃圾填埋等工程领域中十分常见,学者们针对多孔介质热−水−力耦合作用理论开展了一系列研究.Biot[1]将多孔介质视为线弹性体,提出了耦合热弹性理论以消除经典热弹理论中弹性变化对温度没有影响的悖论;Lord 和Shulman[2]发现Biot 理论中因热传导方程扩散而使得热传播速度无限大的错误,通过修正热传导模型建立了Lord-Shulman 广义热弹性理论;Noorishad 等[3]首次推导了饱和土体的温度−应力−渗流耦合基本方程,打开了饱和土体热−水−力三场耦合模型研究的新方向.国内,白冰[4-5]建立了饱和多孔介质热−水−力完全耦合模型的基本控制方程,分析了热源作用下多孔饱和介质的动力响应问题及循环温度载荷的影响;Liu等[6-7]利用Laplace 变换及反变换,分析了一维多孔弹性圆柱以及空腔球壳的热流固耦合问题;熊春宝等[8-10]引入正则模态法对饱和多孔弹性地基热−水−力耦合模型进行求解并分析参数变化对相应物理量的影响;刘干斌等[11]推导了饱和多孔介质热流固耦合效应下的热弹性波动控制方程;陈迪等[12-13]通过建立考虑热渗效应和热流固耦合效应的饱和土体固结方程,研究了圆柱热固结问题;刘硕等[14]提出一种新的近场动力学与有限元法的耦合方法求解材料的热传导问题;朱强华等[15]提出一种基于特征正交分解和有限元法的瞬态非线性热传导问题的模型分析方法等.

以上这些研究基本都是将土体视为各向同性介质,忽略了其本身的各向异性特征.实际上,自然界中绝大多数土体是天然形成的,在产生的过程中由于沉积作用会呈现出各向异性的特征[16].国外,Rajapakse 和Wang[17-18]给出了二维均质半无限大地基在横观各向同性和正交各向异性基础上受简谐载荷作用的位移、应力响应;Abousleiman 和Ekbote[19]以及Kanj 和Abousleiman[20]给出了横观各向同性材料热力学问题的一般控制方程,分析了中空圆柱的热力学特性;Ai 等[21-23]利用不同的积分变换方法研究了各向异性弹性体的热弹动力响应和平面应变问题;Beskou 等[24-25]采用傅里叶级数展开法分析了半无限大各向同性弹性地基上横观各向异性板受到移动载荷作用时的动力响应问题.国内,艾智勇等[26-27]推导了层状横观各向同性地基平面变形问题的解;韩泽军等[28]提出了一种新的算法,用于求解横观各向同性层状地基在时间简谐载荷作用下任意点的应力响应;张春丽等[29-30]基于薄板理论建立了直角坐标系正交各向异性弹性地基上覆无限大弹性板的路基路面三维空间力学模型,推导了板和地基在移动载荷作用下稳态响应的微分方程;郑保敬等[31]提出一种模型降阶方法分析非均质材料结构在复杂载荷作用下的动态响应等.还有一些学者研究了特殊的各向异性参数对土体热−水−力耦合作用的影响,比如Wang 等[32]研究了热传导系数各向异性参数以及渗透系数各向异性参数变化对介质的影响;夏建中等[33]考虑渗透系数各向异性提出了在热源作用下的二维热固结模型;Ai 和Cang[34]研究了渗透系数各向异性参数变化对二维多层地基非轴对称固结的影响等.还有一些学者将孔隙率看做各向同性物理量来考虑孔隙率的影响,比如王立安等[35]基于Biot波动理论,建立了孔隙率、密度、剪切模量和渗透系数相互耦合的非均匀饱和半空间模型;李腾风等[36]考虑了孔隙率变化对热源作用下非饱和土体水热耦合作用影响等.针对孔隙率各向异性的研究较为少见,戴婷等[37]基于功能梯度圆板中细观孔隙依赖于各自组分变化得到整体孔隙计算式,在考虑温度影响下建立了材料湿热模型等.

本文在饱和多孔弹性地基基础上引入孔隙率各向异性参数,并结合Lord-Shulman 广义热弹性理论,建立了考虑孔隙率各向异性的热−水−力耦合动力响应模型并推导其基本控制方程,采用正则模态法对控制方程进行求解,得到了各物理量的解析表达,研究了孔隙率各向异性参数变化对饱和多孔弹性地基的影响.此外,还将控制方程进行退化验证模型的合理性.

1 控制方程

1.1 基本假设

本文将孔隙率各向异性参数引入饱和多孔弹性地基模型中,研究孔隙率各向异性参数变化对饱和多孔弹性地基热−水−力耦合作用下的动力响应问题的影响,基本假设如下:

(1)饱和多孔地基为流固耦合两相介质,内部固体颗粒不可压缩,同时不考虑溶质的影响;

(2)假设地基为二维半无限大弹性体,介质变形为小变形;

(3)孔隙水渗流服从达西定律;

(4)满足Lord-Shulman 广义热弹性理论;

(5)固液两相处于热平衡状态;

(6)假设地基孔隙率处于各向异性状态,假定竖直方向孔隙率为固定参数,水平方向孔隙率由各向异性参数控制.

1.2 问题模型

在地基上表面分别受到温度载荷和机械载荷作用,孔隙率各向异性饱和多孔弹性地基热−水−力耦合问题的计算模型示意图如图1 所示.

1.3 基本控制方程

几何方程

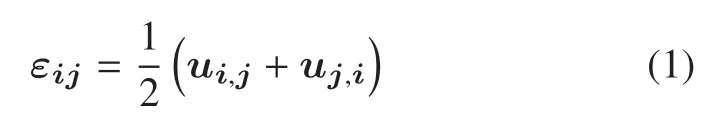
图1 计算模型示意图Fig.1 Schematic diagram of calculation model

式中,εij表示应变张量,ui表示位移张量,“,” 表示对于坐标求导.

本构方程

式中,σij表示应力张量,λ,G表示拉梅常数,e表示体积应变,θ 表示温度变化,θ=T−T0,T表示绝对温度,T0表示初始温度,δij表示Kronecker 符号,β1表示体积应变,β1=(3λ+2G)αs,αs表示土颗粒线性热膨胀系数,P表示超孔隙水压力.

运动方程

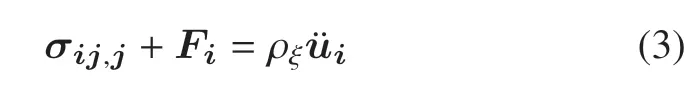
式中,Fi表示体力张量,ρξ表示不同方向的密度,表示孔隙水密度,ρs表示土颗粒密度,字母上方“.”表示对于时间t的求导.

热传导方程

式中,K表示热传导系数,CE表示单位质量介质的比热容,τ 表示弛豫时间.

不计体力的运动平衡方程

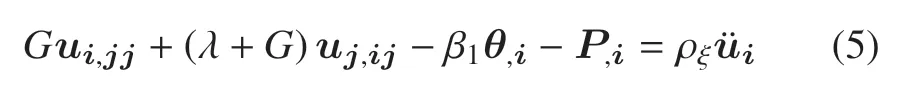
能量方程

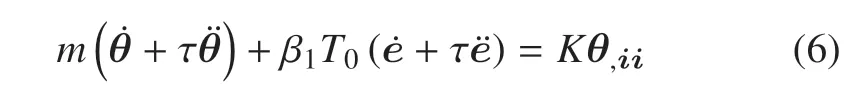
式中,m表示介质比热容,cw表示孔隙水比热容,cs表示土颗粒比热容,.

结合达西定律的流体平衡方程

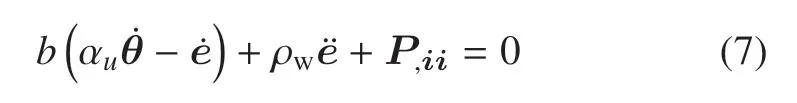
式中,αu表示介质线膨胀系数,αw表示孔隙水线性热膨胀系数,αs表示土颗粒线性热膨胀系数,其中,表示介质的渗透系数,g表示重力加速度,b=ρwg/kd.

基于二维半无限大弹性地基假设,同时为使后续公式推导过程更为简化,引入笛卡尔坐标系(x,y,z),将位移分量表示为ui=(u,0,w).

为使计算结果具有一定的普适性,引入下列无量纲量,该组无量纲量同参考文献[38]

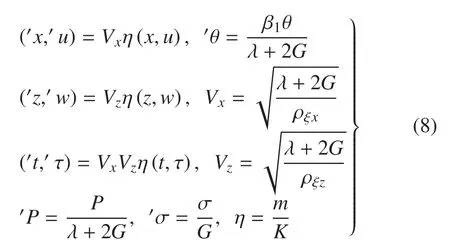
根据方程(8),方程(1)～(7)可简化为(为书写简便,省略点号)

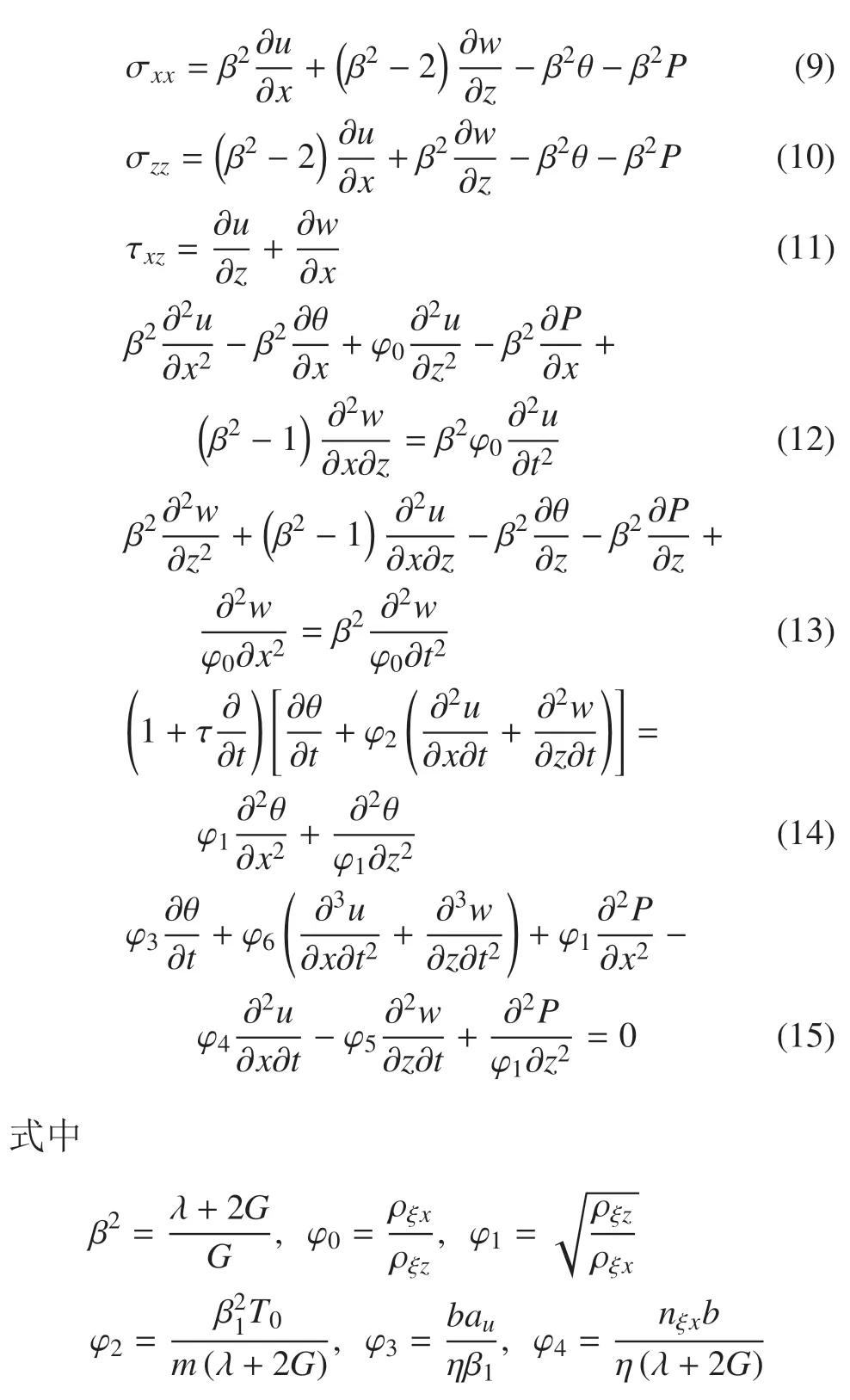
1.4 边界条件

本文讨论地基上表面受到温度载荷、机械载荷作用时的热−水−力耦合动力响应问题,其中边界条件如下.

(1)地基上表面受温度载荷作用

①地基上表面应力自由

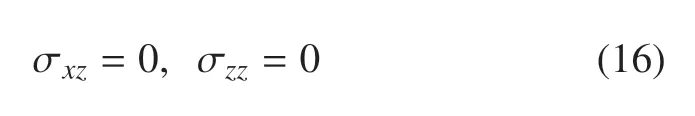
②地基上表面受到温度载荷作用

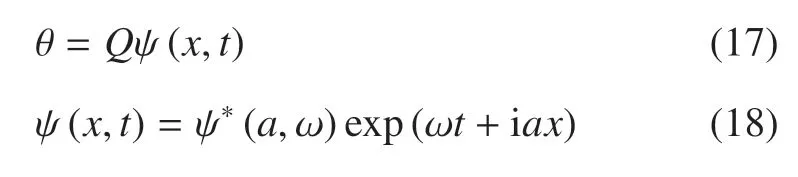
式中,Q表示温度载荷,ω 表示频率(复时间常数),a表示x轴方向的波数,ψ(a,ω)表示载荷振幅,i 为虚数单位,i=.

③地基上表面可透水

(2)地基上表面受机械载荷作用

①地基上表面受机械载荷作用

式中,q表示机械载荷.

②地基上表面不考虑温度载荷

③地基上表面可透水

2 二维热−水−力耦合问题的正则模态分析

所考虑的物理量的解均可以按照以下正则模态的形式进行分解

式中,u(z),w(z),,θ(z),和P(z)分别表示所考虑的物理场的振幅.

对方程(9)～(15)进行正则模态分解可得如下方程

令℘=∂/∂z,对分解后的方程进行简化整理

消去w(z),θ(z)和P(z),可以得到一个关于u(z)的8 阶偏微分方程

将方程(35)因式分解后可得

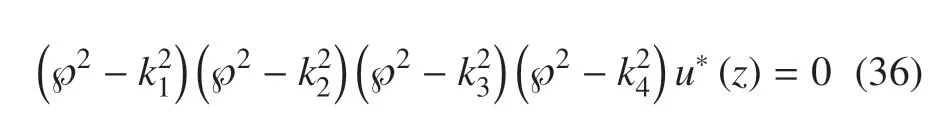
其中

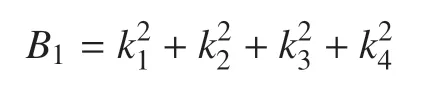
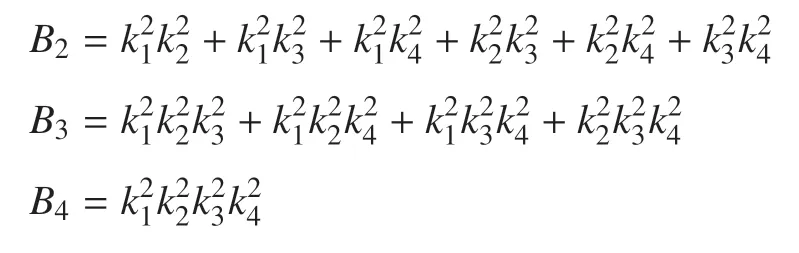
方程的解可表示为如下形式

其中

代入应力分量表达式中得

3 算例分析及结果讨论

以饱和多孔半无限大弹性地基为例,分别在地基的上表面施加温度载荷和机械载荷,研究孔隙率各向异性参数变化对地基深度增加方向和波的传播方向上竖向位移、超孔隙水压力、竖向应力及温度的影响.根据求得的解析解表达式,利用Maple 软件,结合边界条件得到了各物理的分布规律图.

3.1 计算模型验证

本文是考虑孔隙率各向异性参数的影响而建立的控制方程,当孔隙率各向异性参数k=1.0 时方程可退化为各向同性耦合动力响应方程,其结果可与参考文献[38]进行对比,从而验证模型的合理性.

研究中所需要的基本参数取值同参考文献[38]一致,ψ=1,a=1.2.其他参数详见表1.

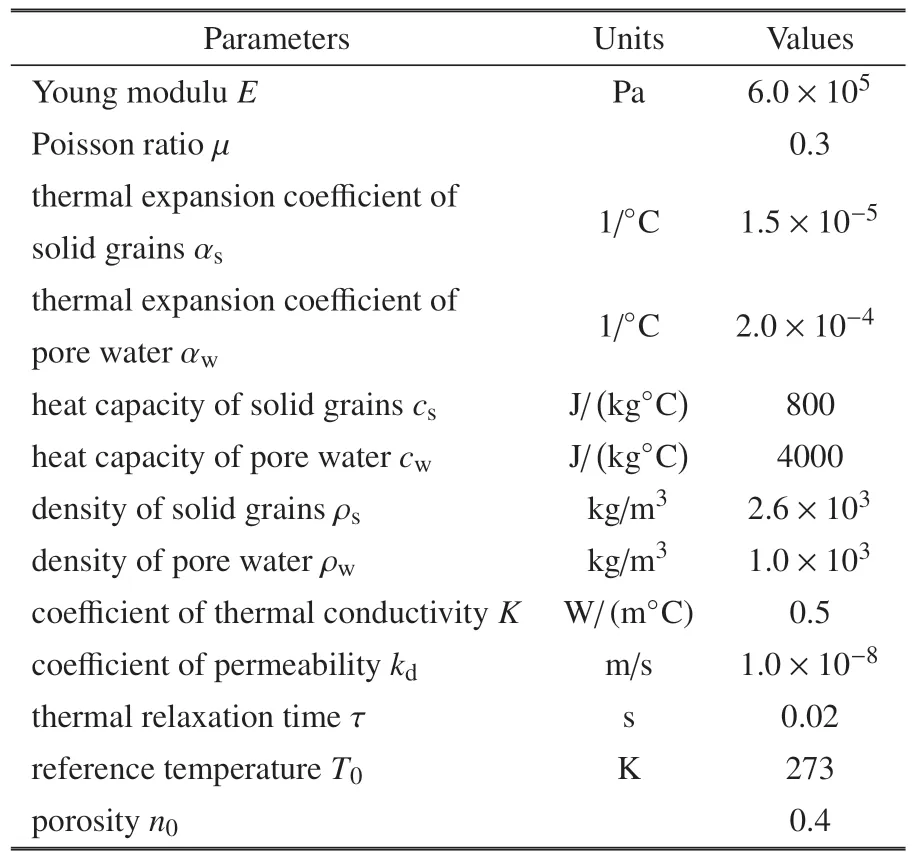
表1 饱和多孔弹性地基热−水−力多物理场耦合基本参数Table 1 Basic parameters of themo-hydro-mechanical coupling of saturated porous elastic foundation

3.2 地基深度增加方向各物理量变化规律

在地基上表面分别施加温度载荷和机械载荷作用,研究地基深度增加方向上孔隙率各向异性参数变化对各物理量的影响.以下8 幅图为x=1.0 平面上t=0.5 时各物理量的变化规律图.其中,退化模型曲线与参考文献结果曲线吻合较好,进而验证了模型的合理性.

图2～图5 为温度载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图,整体来说,孔隙率各向异性参数变化对竖向位移和温度影响较小,对超孔隙水压力和竖向应力影响较大.竖向位移变化趋势都是由压缩状态逐渐转为膨胀最后趋于平缓衰减至零;温度则是逐渐衰减至零.超孔隙水压力曲线和竖向应力曲线峰值均逐渐减小,且峰值出现位置向地基深度减小方向移动,超孔隙水压力减幅为52.72%和61.06%,竖向应力减幅为16.92%和26.13%.这主要是由于孔隙水对温度较为敏感,随着孔隙率各向异性参数增大,两个方向孔隙分布更不均匀影响地基排水速率,进而使得超孔隙水压力变小,而超孔隙水压力变化影响了竖向应力的变化.

图2 温度载荷作用时无量纲竖向位移分布规律图Fig.2 The distribution of non-dimension vertical displacement under thermal load

图3 温度载荷作用时无量纲超孔隙水压力分布规律图Fig.3 The distribution of non-dimension excess pore water pressure under thermal load

图4 温度载荷作用时无量纲竖向应力分布规律图Fig.4 The distribution of non-dimension vertical stress under thermal load

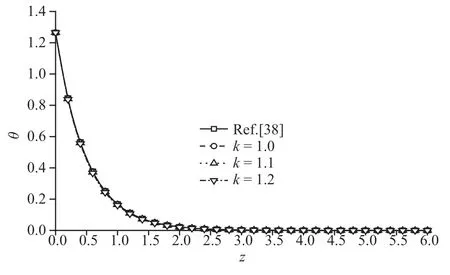
图5 温度载荷作用时无量纲温度分布规律图Fig.5 The distribution of non-dimension temperature under thermal load

图6 机械载荷作用时无量纲竖向位移分布规律图Fig.6 The distribution of non-dimension vertical displacement under mechanical load

图7 机械载荷作用时无量纲超孔隙水压力分布规律图Fig.7 The distribution of non-dimension excess pore water pressure under mechanical load

图6～图9 为机械载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图,整体来说,孔隙率各向异性对竖向位移和竖向应力影响较小,对超孔隙水压力和温度影响较大.图6 和图8 中,竖向位移和竖向应力均逐渐衰减至零,但应力衰减速率比位移衰减速率略快.图7 超孔隙水压力曲线随各向异性参数的增加逐渐减小,尤其是峰值处,有较为明显变化,峰值减幅为8.89%和9.82%;图9 中随着各向异性参数的增大,温度的峰值逐渐减小,减幅依次为18.46%和19.74%.

图8 机械载荷作用时无量纲竖向应力分布规律图Fig.8 The distribution of non-dimension vertical stress under mechanical load

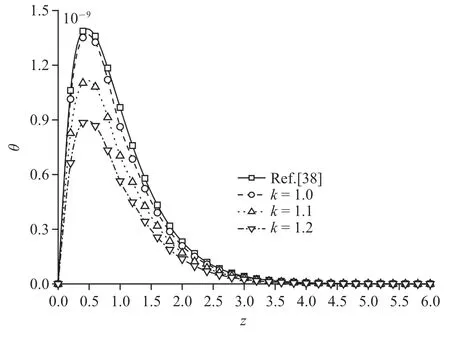
图9 机械载荷作用时无量纲温度分布规律图Fig.9 The distribution of non-dimension temperature under mechanical load

从图6～图9 可以看出,温度曲线量级相对较小,说明单纯的机械载荷作用产生的热量不多,可忽略不计.孔隙率各向异性参数变化对超孔隙水压力和温度的影响趋势相同,但对温度的影响更明显,这是由于随着各向异性参数增大,使得地基热量耗散更为迅速,引起明显的温度变化,而孔隙率各向异性参数的变化影响了地基中孔隙的分布,参数增大,孔隙分布更为不均匀,导致超孔隙水压力峰值减小.

3.3 波的传播方向上各物理量变化规律

本节从波的传播方向上研究了地基上表面分别施加温度载荷和机械载荷作用时孔隙率各向异性参数变化对所考虑物理量的影响.图10～图17 为z=1.0 平面上t=0.5 时各物理量的变化规律图.

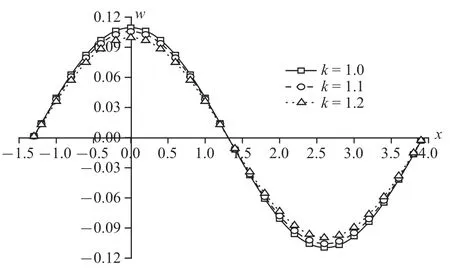
图10 温度载荷作用时无量纲竖向位移分布规律图Fig.10 The distribution of non-dimension vertical displacement under thermal

图11 温度载荷作用时无量纲超孔隙水压力分布规律图Fig.11 The distribution of non-dimension excess pore water pressure under thermal load

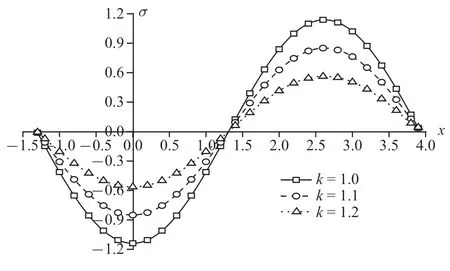
图12 温度载荷作用时无量纲竖向应力分布规律图Fig.12 The distribution of non-dimension vertical stress under thermal load

图10～图13 为温度载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图.整体来说,随着孔隙率各向异性参数的增大,物理量峰值逐渐减小.可以明显看出,孔隙率各向异性参数变化对超孔隙水压力和竖向应力的影响远超于竖向位移和温度.其中,超孔隙水压力减幅依次为53.50%和66.15%,竖向应力减幅依次为25.26%和33.77%,而竖向位移减幅在4%附近,温度减幅稳定在2%左右.这是因为孔隙率的变化影响到孔隙水,随着各向异性参数增大,孔隙分布更为不均匀,孔隙水排出速率受到影响,导致超孔隙水压力减幅明显,而超孔隙水压力变化又会影响竖向应力,使得竖向应力变化.

图13 温度载荷作用时无量纲温度分布规律图Fig.13 The distribution of non-dimension temperature under thermal load

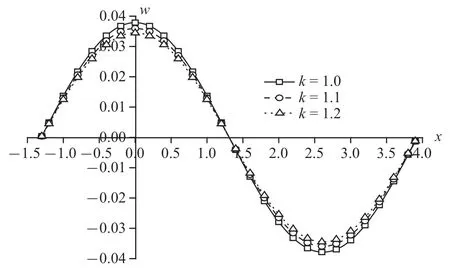
图14 机械载荷作用时无量纲竖向位移分布规律图Fig.14 The distribution of non-dimension vertical displacement under mechanical load

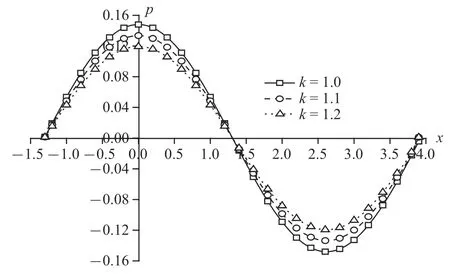
图15 机械载荷作用时无量纲超孔隙水压力分布规律图Fig.15 The distribution of non-dimension excess pore water pressure under mechanical load

图16 机械载荷作用时无量纲竖向应力分布规律图Fig.16 The distribution of non-dimension vertical stress under mechanical load

图17 机械载荷作用时无量纲温度分布规律图Fig.17 The distribution of non-dimension temperature under mechanical load

图14～图17 为机械载荷下竖向位移、超孔隙水压力、竖向应力和温度的变化规律图.孔隙率各向异性对竖向位移和竖向应力变化不太明显,减幅相对较小;对超孔隙水压力和温度变化明显,其中温度减幅更大,为18.46%和19.74%.单纯的机械载荷作用产生于地基中的温度很小,孔隙率的变化使得地基散热更为迅速,所以对温度的影响更加明显.

4 结论

本文在饱和多孔弹性地基基础上引入孔隙率各向异性参数,并结合Lord-Shulman 广义热弹性理论,建立了考虑孔隙率各向异性的热−水−力耦合动力响应模型并推导其基本控制方程,采用正则模态法对简化方程进行求解,得到了各物理量的解析表达,分析了孔隙率各向异性参数变化对相关物理量的影响.主要结论如下:

(1)考虑孔隙率各向异性参数的饱和多孔弹性地基热−水−力耦合动力响应模型可退化为各向同性饱和多孔弹性地基热−水−力耦合动力响应模型,退化后物理量变化规律与参考文献[38]曲线分布规律一致,验证了模型的合理性;

(2)地基深度增加方向上,地基上表面受温度载荷作用时,孔隙率各向异性参数变化对超孔隙水压力和竖向应力影响明显,随着各向异性参数增大,峰值逐渐减小,峰值所在位置向靠近地基上表面移动;地基上表面受机械载荷作用时,孔隙率各向异性参数变化对超孔隙水压力和温度影响明显,随着各向异性参数增大,峰值逐渐减小,峰值所在位置向靠近地基上表面移动;

(3)波的传播方向上,孔隙率各向异性参数变化对各物理量均有影响,使得峰值逐渐减小,地基上表面受温度载荷作用时,对超孔隙水压力和竖向应力影响明显;地基上表面受机械载荷作用时,对超孔隙水压力和温度影响明显.

附 录

εij应变张量

σij应力张量

e体积应变

T绝对温度

δijKronecker 符号

P超孔隙水压力

ρξ不同方向的密度

ρξz竖直方向的密度

ρs土颗粒密度

nξx水平方向的孔隙率

K热传导系数

τ 热弛豫时间

cw孔隙水比热容

αu介质线膨胀系数

αw孔隙水线性热膨胀系数

g重力加速度

ω 频率(复时间常数)

ψ(a,ω) 载荷振幅

ui位移张量

λ,G拉梅常数

θ 温度变化

T0初始温度

β1体积应变

Fi体力张量

ρξx水平方向的密度

ρw孔隙水密度

nξ不同方向的孔隙率

nξz竖直方向的孔隙率

CE单位质量介质比热容

m介质比热容

cs土颗粒比热容

kd介质的渗透系数

αs土颗粒线性热膨胀系数

Q温度载荷

ax轴方向的波数

q机械载荷