二维衰减湍流的速度加速度结构函数1)
周泽友
(清华大学能源与动力工程系燃烧能源中心,北京 100084)
引言
在人们生活的三维世界中,从咖啡的溶解到威力巨大的台风,湍流现象是随处可见的.而在一些自然界与工程应用的三维流动中,由于边界尺寸限制或者外力的作用,其中一个维度上的运动被抑制,流动呈现出近似二维流动的特征.例如大气与海洋中的大尺度流动——由于地球半径约为6400 km,而大气层和海洋的厚度仅为10 km 左右,因此台风等的大尺度运动往往可以被看作二维流动.无论是三维湍流还是二维湍流,湍流场都是一个耗散系统.流场中的湍动能u2/2 会不断被耗散,并需要不断的能量补充来维持稳定的流场.在局部均匀湍流场中,欧拉场的二阶混合速度加速度结构函数(velocity-acceleration structure function,VASF),表示两个粒子间相对湍动能的变化速率,与尺度间的能量传递率相关[1-4]
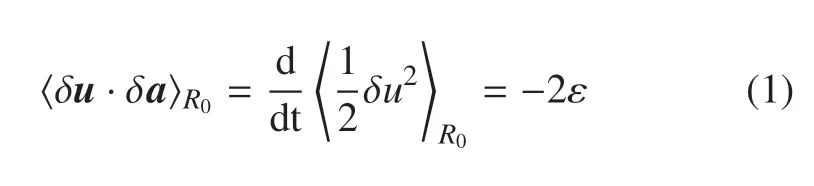
其中,δu和δa为两个粒子间的相对速度和相对加速度,代表系综平均,下标R0表示是对相对距离R0在惯性区的粒子对进行条件统计;ε 为湍流场的能量传递速率,其符号表示能量传递的方向[4].当能量从大尺度传到小尺度,ε >0;当能量从小尺度传到大尺度,ε<0.
在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5],能量耗散率ε >0,<0,并且两者之间的常系数“−2”也在实验中得到验证[6].自然地,人们将式(1)推广到二维湍流的能量惯性区.在二维湍流中,涡量拉伸(vortex stretching)不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用.湍动能将从能量注入尺度LF向更大的摩擦耗散尺度Lα传递,形成反向的能量级串[7-9].此时ε<0,这一点已经在能谱[10],三阶结构函数[11],尺度间的能量传递[12]等方面都得到了证实.但>0 则有待进一步的验证.
二维湍流除了能量的反向传递,另一个重要物理过程是拟涡能(enstrophy,又称为涡量拟能)ω2/2 的正向传递,其中ω 为涡量.外力在作用尺度LF以速率β 注入拟涡能,其不断往小尺度传递,最终在黏性作用尺度η 下被黏性耗散掉.当初始距离在反向能量级串区,式(1)是成立的.当初始距离在正向拟涡能级串区,拟涡能传递率β 起主导.量纲分析可得
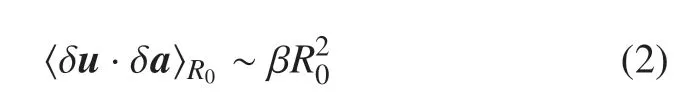
其中,R0为两个粒子的相对距离,正的β 代表拟涡能从大尺度往小尺度进行传递,上式左右两边存在待定的常系数.式(2)只在均匀流场中成立,但实际中的许多湍流场是衰减的.也即拟涡能只在初始时刻或者初始位置上注入,随后注入源消失.例如海洋上形成的强台风,在登陆后由于耗散作用其气旋强度会逐渐降低.
本文将对二维湍流的VASF 进行研究,并重点考察衰减对VASF 的影响.在第1 节推导二维湍流场中正向级串区和反向级串区的VASF 理论公式,发现除了式(1)或式(2)代表的能量或拟涡能在尺度间的传递项外,还存在衰减带来的非均匀项.两者一正一负,呈现竞争关系.第2 节介绍基于皂膜的二维衰减湍流的实验装置.为了获取速度,特别是加速度,以及粒子位置随时间的演化信息,本文采用拉格朗日粒子追踪法对流场进行测量.并实现了在每一步时间匹配推进上,复杂度从N2到Nlog2N的算法优化.第3 节对VASF 在正向拟涡能级串区的测量结果进行讨论.实验发现尺度间拟涡能传递项是正的,但非均匀项为负的,并且占主导作用.因此在二维衰减湍流中VASF 甚至可能会小于0,其符号也失去了表征涡量拟能传递方向的意义.第4 节对与VASF 密切相关的弥散过程进行讨论,通过负的VASF 解释了弥散过程后期变慢现象.最后一节对本文工作进行总结.
1 理论
对于二维流场中的任意时刻上的任意两点(x,t)和(x0,t0),这里以及下文中的上标0表示另一个点的信息.这两点距离为r=x−x0,中间位置为X=(x+x0)/2.时间间隔为τ=t−t0,平均时间为T=(t+t0)/2.两点的速度为ui(x,t)和,加速度分别为ai(x,t)=和=.那么速度和加速度的混合结构函数为

其中相对加速度中的相对对流项为
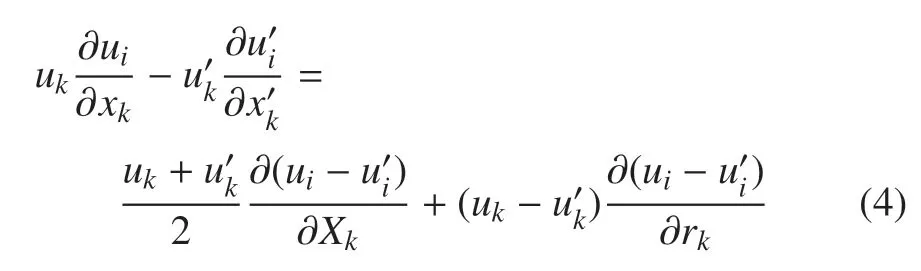
上式中用到了空间坐标自变量(x,x0)与(X,r)的相互转化[13]
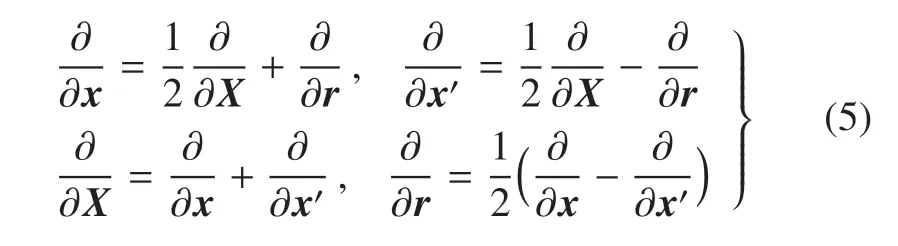
同理可以得到相对加速度中的非稳态项为
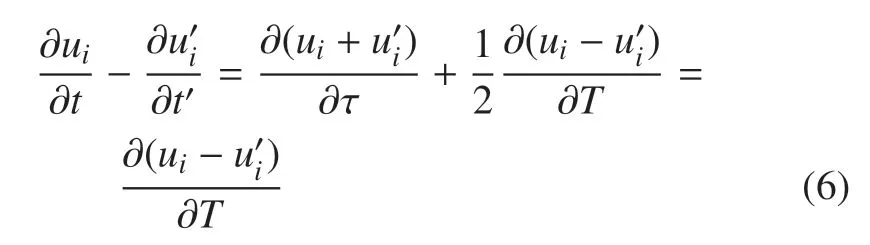
将式(4)和式(6)代入到式(3),取其缩并,系综平均得到
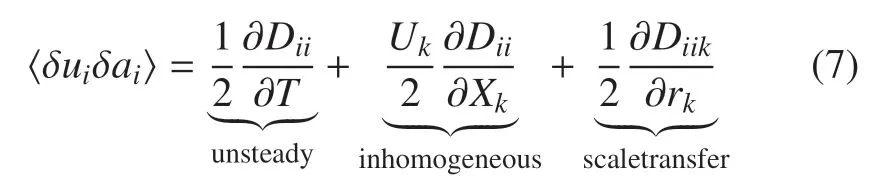
其中,U=(u+u0)/2 是流场的平均速度,Dii=和Diik=分别为二阶和三阶的欧拉速度结构函数.上式的推导是一个通用的表达式,并未用到任何假设.VASF 虽然是绝对坐标X和相对距离r的多元函数,但是这两个自变量之间没有显著耦合(即使Dii,Diik是这两个自变量的二元函数),这为实验数据的分析带来了极大的便利.可以看到由3 部分组成.第1 项为时间的非稳态项,在稳态流场中为0.第2 项是非均匀项,在局部均匀流场中结构函数Dii只是相对距离r的函数,对当地绝对位置X微分为0.因此在稳态局部均匀流场中,只剩下第3 项.同三阶速度结构函数物理含义一样,该项代表能量或拟涡能在尺度间的传递.第3 项在任意流场中是没有普适表达式的.为进一步对该项进行分析,本文讨论该项在不可压均匀各向同性湍流的条件下的表达式.参考三维湍流中相关推导[14-16],本文得到二维和三维湍流中该项的通用表达式
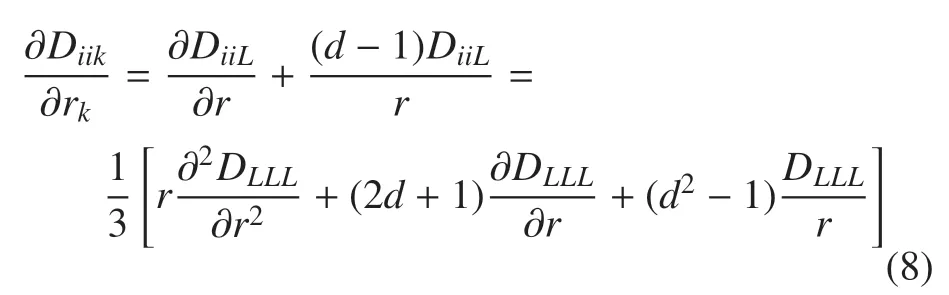
其中,d代表维数,在二维湍流中d=2,在三维湍流中d=3.,下标L表示相对速度在相对距离径向方向的投影.进一步的,DLLL=为三阶径向速度结构函数,在能量和拟涡能惯性区分别为[16-17]

将式(9)代入式(8),得到VASF 中的能量/拟涡能在尺度间传递项的表达式

式中,ε >0,β >0 代表着能量和拟涡能分别从大尺度传向小尺度.在三维均匀各向同性湍流中,能量往小尺度传递,=−2ε <0.而在二维均匀各向同性湍流中,能量往大尺度传递,拟涡能往小尺度传递,所以两个惯性区间>0 皆成立[18-19].
本文从相对速度和相对加速度的定义出发,重现了在均匀各向同性湍流中式(1)和式(2)的VASF 表达式,并确定了在拟涡能级串惯性区表达式前的系数“1/2”.而在一般湍流场中,VASF更普适的表达式中包含时间维度(非稳态项),空间维度(非均匀项),尺度维度(尺度间传递项)三者共同的影响.为比较这三项的相对大小,本文开展了基于皂膜的二维衰减湍流实验研究.为此接下来一小节先对实验装置及流场测量方法进行介绍.
2 实验方法和粒子跟踪技术
二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20-21].实验上,Couder 提出了基于皂膜的实验装置[22],并得到了广泛应用[23-27].在前人工作的基础上,本文搭建了皂膜流动实验台.其详细描述可参考之前的报道[28-29],本文在此进行补充说明.皂膜实验装置如图1(a)所示.含2% Dawn 洗碗液的皂液沿着直径为6 mm 的狭长喷嘴流出.在喷嘴出口处,两根直径为0.32 mm 的红色尼龙绳组成了长X1=106 cm 的逐渐扩张平面.皂液在此逐渐展开形成皂膜,并被重力不断加速.在长X2=194 cm,宽W=5 cm 的实验段达到充分发展.最后流入下水箱,被蠕动泵送入上水箱,形成往复循环.通过调整泵的流量,皂膜的平均速度可在1~3 m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在4~9µm 之间[29],小于另外两个维度四到六个量级,因此可以被视为二维湍流.本文的皂膜流量工况为40 ml/min,平均流速为2.7 m/s.
为了形成强湍流场,类似于三维风洞中插入平面栅格的方式,本文在皂膜上游处水平插入一排栅格,如图1(a)中虚线方框中所示.栅格间距M=5 mm,组成栅格的圆棒直径为1.14 mm.栅格的布置实物图如图1(b)所示,栅格是以一块铝板为基底,在表面通过线切割开半圆形槽,放入不锈钢针作为圆柱小棒制成,并以磁铁加以固定.图中两根竖直的亮线为构成皂膜的两根尼龙绳,皂膜在两根尼龙绳中间往下流动.
当皂膜流过栅格后,会形成强烈湍流脉动.本文在距离栅格为S=(12.5~67.5)M的下游位置对流场进行测量,如图1(a)中的绿色区域.在对流场进行速度测量时,粒子图像测速法(particle image velocimetry,PIV)是一个成熟和普遍使用的方法,该方法可以获得速度的欧拉场.但利用欧拉速度场求取加速度时,涉及到对流项的空间求导,要求流场空间分辨率应达到拟涡能耗散尺度的量级.此外湍流中的非稳态项∂ui/∂t和对流项uk∂ui/∂xk两者十分接近且正负相反,利用这两者的和得到的加速度不确定度往往极大[30].为此本文采用拉格朗日粒子追踪法(lagrangian particle tracking,LPT)对速度和加速度进行测量[31].首先在皂液中加入直径1µm 的示踪粒子,粒子直径小于皂膜厚度,因此可以忽略对皂膜的影响.一台波长532 nm,功率为100 W 的脉冲激光器照亮待测流场区域中的示踪粒子.如图1(a)所示,两台高速相机沿流向依次排列,在保证分辨率的情况下获得足够长的流场视野.两台相机的合成分辨率为(2×)2560×472,可以拍得100 mm×12 mm 的狭长流场区域.通过移动相机和栅格的相对位置实现更长范围内的测量.采用同步器将两台相机和激光器进行同步,采样频率为5000 Hz.整个实验系统通过基于Qt环境下编写的数据采集平台进行控制,实现数据的自动采集、传输和存储.

图1 (a)二维水洞装置图,x 方向为重力方向,y 方向为水平方向,z 方向为皂膜厚度方向.皂膜平面由两根直径为0.32 mm 的尼龙绳组成.为了形成湍流场,在皂膜上游水平插入一排栅格.激光器照亮距离栅格为S 的下游绿色区域,该区域内的流场轨迹信息被两台高速相机捕捉.(b)栅格布置的实物图.上方水平排列的圆柱小棒为栅格,竖直的亮线为尼龙绳,两根尼龙绳中间为竖直往下流动的皂膜.由于532 nm 激光的散射,整个流场呈现绿色背景Fig.1 (a)Two-dimensional water tunnel setup, x axis is the gravity direction,y axis is the horizontal direction,z axis is the film thickness direction.The plane of soap film is consisted by two nylon ropes whose diameter are 0.32 mm.To create turbulent flow,we insert a comb in the upstream.The laser illuminates the downstream regions below the comb,whose flow trajectories are recorded by two high speed cameras.(b)The real image of comb equipment.The upper cylinders make up a comb,the vertical bright lines are nylon ropes,and the soap film flows down between the ropes.The whole flow are in green background,owing the scatter from 532 nm laser
在获得原始的粒子图像后,首先通过亚像素定位获得示踪粒子在像素坐标系上的位置.第二步经过标定还原到真实的物理空间坐标系.对于单台相机的二维标定,一般是假设皂膜平面和标定板平面重合.但在两台相机的二维标定中,可以求得皂膜平面和标定板平面的距离并调节使之真正重合.接下来一个重要的步骤是实现粒子在不同时刻的匹配,这是LPT算法的核心以及计算资源消耗最大的一步.每一个瞬时场都有数百个粒子,从上一个时刻到下一个时刻需要实现这上百个粒子的一一匹配.由于粒子的形态大小是无法区分的,因此一般是通过历史的位置、速度和加速度场信息进行匹配[31].假设每个时刻粒子平均个数为N.若采用暴力匹配算法,对t时刻的Nt个粒子,需匹配t+1 时刻的Nt+1个粒子,每推进一个时间步的复杂度为N2.但本文注意到皂膜流场是长100 mm 的狭长形区域.流场的竖向脉动速度方差约为0.2 m/s,考虑到大约5 倍脉动速度的事件概率很低以致可忽略不计.那么在高达5000 Hz 的拍摄频率下,粒子的位置波动为0.2×5/5000=0.2 mm.因此本文事先就可以预估出粒子下一个时刻的位置限定在±0.2 mm 范围内,而不必在整个100 mm 的流场范围内进行匹配.
基于上面的分析,本文提出实现粒子时间匹配的两步走快速匹配算法.首先对每一个时刻内的流场粒子以x坐标为基准进行排序,例如快速排序等,复杂度为Nlog2N.其次在已经排序好的t+1 时刻流场中,通过二分查找等算法迅速完成±0.2 mm 位置范围的定位,复杂度为log2N.对这±0.2 mm 预判区的粒子进行一一匹配,一般预判区内粒子个数为O(1).这一个步骤需要对t时刻的每一个粒子进行依次操作.因此每推进一个时间步的复杂度为

为此基于对特定流场的分析实现了快速的LPT 算法.其实也可以在亚像素定位步骤中,按照x坐标依次遍历识别粒子,从而节省上述算法中的空间排序步骤.此外实际计算中,为了保证匹配准确率,本文会同时验证t+1 时刻和t+2 时刻的粒子信息.为了表述方便,上文中只阐述根据t+1 时刻信息进行匹配的算法.但两种算法都可以通过上面的思路进行改善,将推进复杂度从O(N2)降低至O(Nlog2N).匹配问题体现在生产生活中的方方面面,本文提出的O(Nlog2N)匹配算法是基于粒子位置信息的强预测性.对于有着同样性质的问题,可以将本文思路进行推广并应用.
在获得流场轨迹信息后,最后一步是通过位置场进行速度和加速度场的计算.根据粒子轨迹信息,可以通过对空间位置的一次时间微分得到速度.进一步地,直接对空间位置的二次时间微分得到加速度,而不需要通过速度场再来计算加速度,从而LPT方法实现了加速度的准确测量.实际计算中,由于轨迹信息在时间上是离散的,一般是通过对位置信息卷积速度核函数和加速度核函数以分别得到速度和加速度[31].
3 VASF实验结果与讨论
通过LPT测量,本文获得了皂膜流场中粒子轨迹上的速度和加速度.进一步对轨迹进行时间排序,得到速度和加速度的欧拉场.假如本文对欧拉场中任取两点来计算式(7)中的VASF 或者两阶及三阶速度结构函数,那么得到的将是待测区域的统计特性的平均值.但皂膜流场的脉动速度在主流x方向是不断衰减的,β 和ε 都是空间位置x的递减函数.理想情况下,按照定义式(7),要想计算各部分在当地位置x的值,需要选取x−r/2 和x+r/2 两个点的速度进行计算.但实际上这样的数据点极少,难以形成收敛的统计量.为了获取收敛的结构函数,本文采用泰勒冻结假设.流场的脉动速度u虽然在不断衰减,但平均速度U=2.7 m/s 几乎保持不变.流场的湍流强度,因此满足泰勒冻结假设[32].泰勒冻结假设并非适用于所有的流场,但在三维风洞中的运用已经得到广泛的认可[33].Belmonte 等[34]在二维皂膜流动中,也已经验证了泰勒冻结假设的正确性.该假设认为湍流场的信息被冻结着以对流速度进行传递,那么
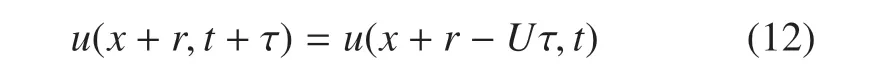
因此速度的二阶结构函数为
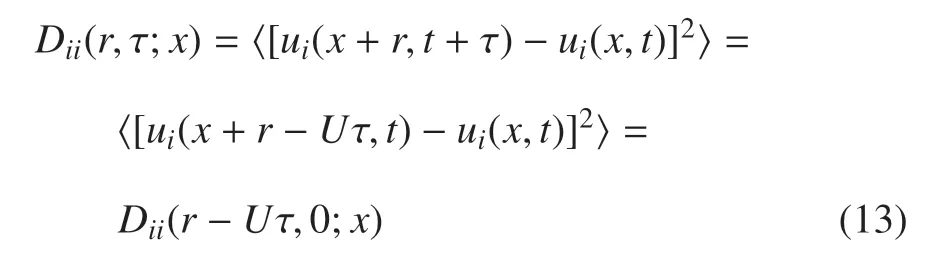
在风洞中使用热线法测速时,也是利用泰勒冻结假设获得在热线当地位置处的结构函数[35],自变量相对距离只包含时间距离.相同的,式(13)参与运算的是两个在当地位置x的点的脉动速度信息,得到的是当地x的二阶结构函数.唯一不同的是,这里自变量相对距离r−Uτ 既包含两点之间的空间距离r,也包含时间距离τ.为了获得当地位置x上的真实条件统计,空间波动范围r的选取不宜太大.一般的,本文设置其最大值为r=0.2 mm,也即计算在位置x±0.2 mm 处的当地统计特性.r的范围是根据拟涡能耗散率尺度选定的,其值为0.3~0.5 mm[28],并随着往下游的发展而逐渐增长.
图2(a)展示的是利用泰勒冻结假设计算得到的,当地位置x的二阶结构函数Dii(r;x).如右边的颜色坐标所示,不同的颜色代表不同的当地位置x.在距离栅格下游的12.5M一直增长到67.5M,颜色也从深蓝变为深红.根据Kraichnan 的理论[7],在正向拟涡能级串区,结构函数由β 控制.量纲分析得到Dii~β2/3r2.图2(a)显示在r 图2 (a)运用泰勒冻结假设,计算当地下游位置x±0.2 mm 处的Dii 与尺度r 的关系.不同的颜色代表对应的距离栅格的距离x/M.两台相机一次的拍摄视野只有100 mm=20M.为获得距离栅格更宽范围的统计特性,本文通过移动栅格使相机距离栅格S/M=12,20,30 和50,分4 次实验完成.(b)−<δuiδai>与尺度r 的关系,在正向级串区表现出r1.5 的幂次律.图中的各颜色代表不同的空间位置,同(a)中一致.本图和上图的竖直实线为尺度r=0.35M,其与各种颜色线的交点即为各下游位置在r=0.35M 上的−<δuiδai>和DiiFig.2 (a)Using Taylor frozen flow hypothesis,we calculate the relationship between Dii and r in local downstream location x±0.2 mm.Different colors correspond to different separation below the comb x/M.The capture window of two cameras is 100 mm=20 M in each time.To obtain a wider regions statistics,we set the relative separation between camera and comb as S/M=12,20,30 and 50.(b)The relationship between −<δuiδai>and r,which shows r1.5 power law in direct enstrophy range.The colors mean different downstream locations which are the same with(a).The vertical solid line lies in r=0.35M,whose cross points with different colorful lines are −<δuiδai>and Dii in r=0.35M 同计算式(13)一样,运用泰勒冻结假设,本文也计算了各下游位置的VASF,如图2(b)所示.在二维均匀各向同性湍流中,式(10)表明无论在正向级串区还是反向级串区,VASF 的尺度间传递项,.但实验结果显示所有下游位置的所有尺度上VASF<0.而皂膜实验是稳态的,构成VASF 的第一项为零.因此这告诉人们构成VASF 的第二项,非均匀项不可忽略.并且非均匀项为负,即使尺度间传递项为正,但由于非均匀项绝对值更大,导致整体的VASF 为负.在正向级串区中,非均匀项 其中,DNN=为二阶横向结构函数,δuN为相对速度在垂直于相对距离方向上的横向分量.由于皂膜平均速度U=2.7 m/s 几乎保持不变,因此本文将空间变量换为时间变量x=Ut.在均匀各向同性二维湍流的正向级串区,Dii=4DNN/3.上式第二个关系是考虑到正向区的速度场是线性的,将相对速度进行泰勒展开并只保留第一阶项,δru~ωr.最后一个关系是由于β=−d(ω2/2)/dt.可见非均匀项对VASF 是负的贡献,与预期一致.此外在均匀各向同性湍流场中,其随尺度的幂次律为r2.非均匀项与尺度间传递项虽然有着相反的符号,但有着相近的幂次律,也与图2(b)实验测得的综合VASF 的r1.5幂次律十分接近.出现的幂次律偏差可能和Dii一样,是由于有限惯性区间等因素导致. 通过上述的分析,本文发现实验结果中负的VASF 很有可能是流场非均匀性导致.接下来,本文对此进行定量的计算和比较.对于VASF,实验中可以直接测得在不同位置和不同尺度下的值,如图2(b)所示.选定正向级串区的某一个尺度r=0.35M,图2(b)中的竖向与各颜色曲线的交点,即为不同位置x处在r=0.35M的值.这些值如图2(a)中的红色圆圈所示,其随着往下游的发展而逐渐衰减.对于组成VASF 三部分分量,如式(7)所示.其第一项为0.对于第二项,在均匀各向同性湍流中,本文可以得到其理论的表达式(14).而皂膜流场并不满足均匀各向同性的条件,本文转而采用实验直接测量的方式.同VASF 一样,图2(a)中的竖向与各颜色曲线的交点,即为不同位置处Dii(x)=Dii(tU)在r=0.35M的值.对其进行对空间求导,可获得非均匀项.其值小于0,本文对其取负号,如图3(a)的绿色方块.因为采样点比较离散(分辨率为0.5 mm),进行微分操作后数据点有一定的离散.但不难看出,非均匀项的值与VASF的值十分接近,且变化趋势高度一致.进一步的,将两者画成散点图,如图3(b)所示,中间的实线表示两者完全相等.而实验数据几乎落在直线附近,表明两者几乎相等,两者的相关系数为0.905,平均值相差6%.在正向级串惯性区的其他尺寸,如r=0.15M和r=0.85M也观察到同样的现象. 图3 (a)在尺度r/M=0.35 下,红色圆圈为VASF,对其取负号使之为正.绿色方块为构成VASF 的第二项,非均匀项,并也对其取负号.蓝色星形为构成VASF 的第三项,尺度间传递项的实验值.这三者在不同空间位置tU/M 的值.(b)纵坐标为−<δuiδai>的对数值,横坐标为−<(Un/2)∂Dii/∂Xn>的对数值,数据基本都落在图中等值线附近Fig.3 (a)In scale r/M=0.35,the red circles are VASF which have been multiplied by −1.Green squares are inhomogeneous term which is the second term of VASF.Blue stars are the scale-to-scale transfer term which is the third term of VASF.We plot their values in different downstream location tU/M.(b)The ordinate is the logarithmic value of−<δuiδai>,the abscissa is the logarithmic value of−<(Un/2)∂Dii/∂Xn>,most of the data lies around the contour line 现对构成VASF 的第三部分,代表能量和拟涡能传递的(1/2)∂Diik/∂rk进行讨论.流动的衰减主要是在主流x方向,因此本文可以通过对x方向求导,进而获得非均匀项.但能量和拟涡能的传递在各个方向是同量级的,在均匀各向同性湍流场中是相等的,本文无法选择球坐标系中某一个方向rk进行求Diik的微分.为评估该式大小,本文采用均匀各向同性湍流场中的结果.根据式(10),在正向级串区,(1/2)∂Diik/∂rk=βr2/2=4DLLL/r.通过泰勒冻结假设,获得DLLL(t;r=0.35M).从而得到(1/2)∂Diik/∂rk在尺度r=0.35M上的值,如图3(a)中的蓝色星形所示.可以看到代表拟涡能在尺度间传递的该项在各空间位置上都为正数.由于数据是在长度为±0.2 mm 的狭窄区域进行统计,并且三阶矩收敛性较二阶矩更差,因此数据的波动比较大.但依然可以看到蓝色数据约为红色和绿色数据的1/2~1/4.并且随着往下游的衰减,相差会越来越大.可见在衰减的皂膜流场中,是非均匀项对VASF 占主导. 在二维衰减湍流中,尺度间的传递项始终为正.说明了即使是在衰减流场中,拟涡能也是往小尺度传递.衰减效应对二维湍流拟涡能的传递方向不会造成本质的影响.但衰减会对VASF 造成显著的影响.由于非均匀项为负值,即使尺度间的拟涡能传递项为正值,VASF 仍为负值.在非均匀二维湍流中,本文从理论上发现不可以忽略非均匀项的效果,进一步从实验上发现该项甚至会主导VASF.关于三维湍流中非均匀项对VASF 的影响还有待进一步研究. VASF除了表征尺度间的能量/拟涡能传递,也和湍流场的弥散作用密切相关.弥散过程描述了粒子位置随时间的演化.这是人们日常生活中的一种常见的物理现象.例如PM 2.5 颗粒在大气中的运动,污染物在海洋中的扩散,病毒在人群中的传播.研究弥散过程可以帮助人们理解、预测、还原追踪这些过程.其可通过考察两点的相对距离平方随时间的演化来进行研究,其中x0(t)和x(t)分别为两个粒子在时刻t的空间位置.下标R0表示对初始距离为R(0)=R0且在惯性区的两个粒子做系综平均.当弥散时间不太长时,本文对R(t)进行在t=0 时刻进行泰勒展开[6,37] 其中,δu0和δa0分别为t=0 时刻的相对速度和相对加速度.那么.本文接下来只选取在正向级串区的R0粒子对进行讨论.主要是考虑到,在皂膜流场中,空气阻力带来的能量衰减主要集中在大尺度.此外若初始尺度R0在反向级串区,R(t)很快将会超过流场的相关尺度.此时两个粒子不再相关,会进入Taylor 线性弥散区间,也即. 图4 (a)在距离栅格20M~40M 范围内,两个粒子对的相对距离平方<(R(t)−R0)2>随着时间的关系.不同的颜色代表不同的初始距离R0.子图的黑色直线为(t/τF)2,并不是数据拟合曲线.(b)考虑VASF 对相对距离的影响后,补偿的弥散关系Fig.4 (a)In the region which lies in 20M~40M below the comb,the dispersion relationship of two particles <(R(t)−R0)2>with time.Different colors correspond to different initial separations R0.The black line in sub-figure is(t/τF)2,which is not the fitting curve.(b)Considering the effect of VASF,the compensated dispersion relationships 从子图中可以看到在各个尺度上,相对距离平方都呈现出t2的增长规律,表明式(15)中的第一阶t2项在初始时刻是明显的主导作用.当用来归一化纵坐标,各个尺度的数据都落在同一条黑色直线(t/τF)2上,进一步验证了式(15),并与Batchelor[39]提出的弥散过程中t2理论一致.但发展一段时间之后,例如t>0.8τF,可以看到相对距离平方的发展比t2要慢.这种变慢的弥散过程可以从主图中更明显地看出来,主图是用来无量纲化纵坐标.假如式(15)中只有t2项,那么数据应该落在值为“1”的水平虚线上.但在t>0.2τF之后,出现了更加缓慢的增长.此时(R(t)−R0)2=1~2 mm,相对距离R(t)仍在惯性区范围内,甚至还是在正向级串区.两个粒子还表现出相关性,大尺度的影响也应该很微弱.说明主要是式(15)中的t3项起到显著影响.t3项和t2项的相对关系为 其中C1=O(1),C2=O(1)分别为VASF 和二阶速度结构函数的常系数.可见在t=C2τF/C1时t3项将不可被忽略,这与本文的观察一致.在二维均匀各向同性湍流场中,>0,从而t3项是正的,会使得后期的弥散过程比t2更快,与本文的实验观察相反.对于这一矛盾,本文可以通过上一节关于VASF 的讨论来解释.在衰减流场中,VASF 是负的非均匀项和正的尺度间传递项相互竞争的结果.若衰减效应足够强烈,非均匀项足够大,VASF 是可能小于零.因此本文在弥散过程中看到的负的VASF 和二维湍流中正的尺度间拟涡能传递两者并不矛盾. 为了进一步验证VASF对弥散过程的影响,本文绘制补偿VASF的粒子相对距离平方随时间的演化,如图4(b)所示.可以看到各个尺度都很好的落在理论值“1”附近.出现的些许波动可能是由于粒子对的初始距离选取有一定的容差R0±0.5 mm.在t>0.5tF之后,粒子的相对距离R(t)≈10 mm,相关性逐渐减弱,转到泰勒线性扩散区间.由于初始尺度R0越大,越快进入该区间,因此可以看到红色曲线代表的大初始尺度也越早出现偏离.由此本文定量上解释了弥散过程在后期变慢是由于负的VASF 项导致. 一直以来,湍流场中的二阶速度加速度结构函数(VASF)被认为与能量或者拟涡能在尺度间的传递相关.本文从加速度定义出发,发现VASF 除了尺度间传递项,还有非稳态项和非均匀项.在稳态的局部均匀各向同性湍流中,只有尺度间传递项.但实际湍流流动中,很多都是衰减的非均匀湍流.为研究非均匀项对VASF 的影响,本文搭建了基于皂膜的二维衰减湍流.通过LPT 测量方法及改进的Nlog2N的粒子匹配算法,获得了速度场和加速度场.实验数据显示二维湍流尺度间传递项在正向级串区的尺度间传递项均为正,证实了拟涡能往小尺度传递,说明衰减并不影响其传递方向.采用泰勒冻结假设,得到当地空间位置的非均匀项.在衰减湍流中,非均匀项为负,并且大于正的尺度间传递项.因此是非均匀项主导二维衰减湍流的VASF,使之为负数.最后本文对与VASF 密切相关的弥散过程进行了讨论,实验观察到两个粒子相对距离平方先以t2幂次律增长,之后变为更缓慢的增长.这种缓慢增长可以用负的VASF 来解释,也即是由于衰减放缓了弥散过程.总的来说,本文通过理论分析和LPT的实验结果发现衰减不改变拟涡能的传递方向.但是衰减在VASF 和弥散过程等问题上会产生显著的影响,在这些问题的讨论上衰减作用将不可忽略. 致谢感谢徐海涛教授对本工作的指导和建议,感谢清华大学对本工作的资助.由衷感谢审稿人给出的宝贵意见使得本文得到进一步的改善.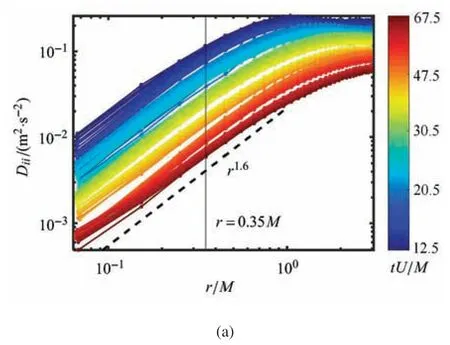

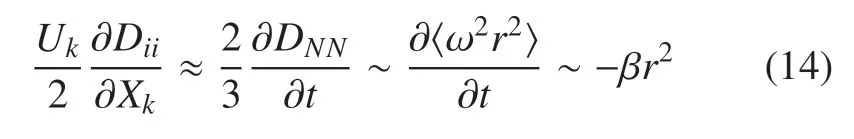

4 弥散
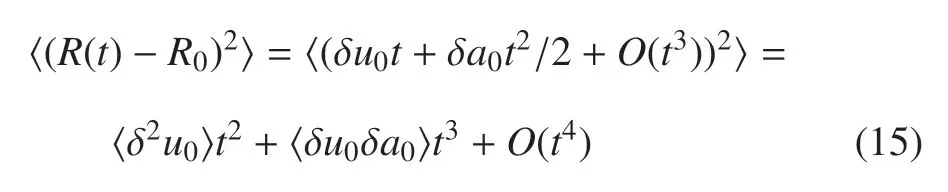


5 结论

