基于傅里叶定律的高温作业服装设计研究

杨振华 吴雪琛 蓝妙敏

（1、广西师范大学电子工程学院，广西 桂林541000 2、南京邮电大学计算机科学与技术学院，重庆400065）

1 概述

保持体温恒定是人类得以生存的重要手段，但过高的温度也会给机体的各个方面带来严重危害，轻则导致机体受损，重则威胁生命[1]。因此在高温环境下工作时，人们需要穿着专用服装以避免灼伤。专用服装通常由三层材料材料构成，记为I、II、III 层，其中I 层与外界环境接触，III 层与皮肤之间还存在空隙，将此空隙记为IV 层[2]。为设计专用服装，将体内温度控制在37℃的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度[3]。研究目的是降低研发成本、缩短研发周期。

2 模型的建立与求解

2.1 背景知识

（1）傅里叶定律传热模型推导

传导热量与温度梯度、传热面积和传热时间为正比：

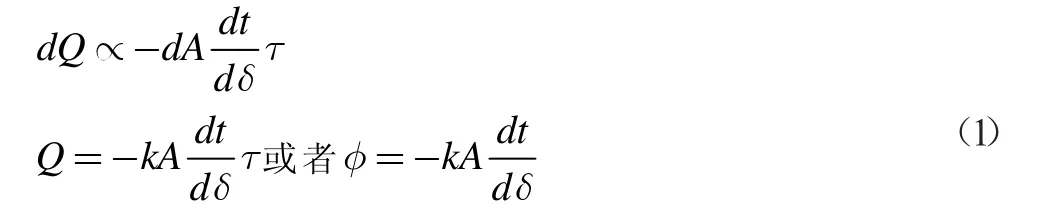
其中φ=Q/τ 表示传热速率，单位为W；A 表示表面面积，单位为m2；k 为比例系数，又称为导热系数，单位为W/（m*℃），负号表示热流方向总是和温度梯度方向相反。

（2）热导系数（热导率）的相关解释

导热系数的推算：

导热系数越大，即物体的导热性能越好，即在相同的温度梯度下传热速率越大。对大多数固体，k 值与温度大概成线性关系，对于纯金属，温度越高，导热系数越小，纯度越高，导热系数越大；对于非金属，温度、纯度越高，导热系数都越大。而气体导热系数低，并且随着温度的升高，导热系数增大。故气体材料适用于保温隔热。

（3）热传导传热计算

多层平壁的热传导示意图：

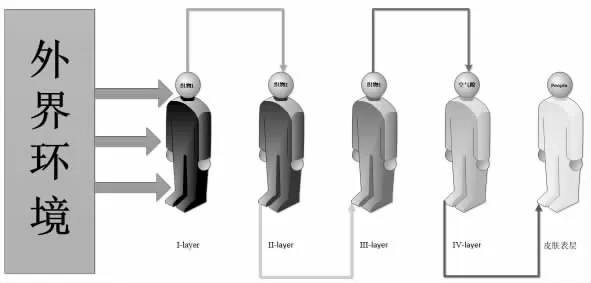
图1 多层平面壁的热传导示意图

2.2 模型建立与求解

首先本文假设三层材料之间是无缝连接，而第IV 层（空气层）厚度在0.6-6.4mm 之间，即空气厚度恒小于6.4mm，热对流对热传导的影响很小，故本题不考虑热对流对热传导的影响。要对传导模型进行求解计算，还需要知道壁面热流。由于壁面热流=材料导热系数*（较高温表面温度- 较低温表面温度）/厚度，故有如下求壁面热流公式：

然后由题目分析可知本题主要考虑热传导和热辐射，故先从热传导开始讨论。一维热平面热传导速率方程为：

接着本文基于热传导领域前辈torvi 的研究成果的基础上，建立了多层材料的温度分布微分等式：

紧接着本文又对热辐射进行了讨论，不同材料表面的热辐射能量Q 为：

其中m，n 分别表示不同的材料表面位置，一般来说是高温位置减去低温位置。具体温度区分表达如下：

自此，只要确定边界值便可对整个传热模型求解完成，因此考虑其起始条件和边界条件：

将题目所给数据中“皮肤最外侧温度分布表格”用MATLAB进行数据拟合可得到拟合曲线。由拟合曲线可得皮肤最外侧温度和时间的拟合关系式为：

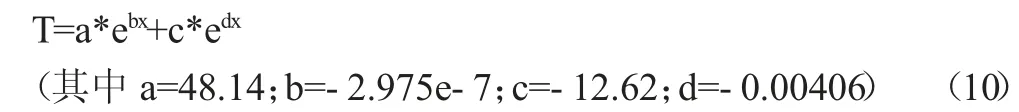
再将题目中已给参数如密度、热导率、比热等以及后续计算得来的壁面热流等代入到上述公式中，由Matlab 可以求解出其整体三维温度分布图。由上图可知，图中的横坐标x 表示水平坐标，从“0”开始即表示此过程的初始位置为假人皮肤外侧，依次向防护服外侧延伸。若将整个防护服材料看作一个均匀质体，这个质体肯定对应这几层材料中的某一水平坐标，故运用此原理可以的求出此坐标下的温度分布图。但这只是个例子，不是解题过程，仅仅当做举例说明。由温度分布图便可以读出一定坐标下的温度度分布，本文采取的是选取四个典型的位置，即每层材料的中心位置（包括空气层），故同理可得四层材料的三维温度分布三维图和四个位置的温度分布数据图。具体如下：

第I 层的温度分布三维图和材料层中心坐标处温度分布数据图：

图2 第I 层中心坐标处温度分布三维图

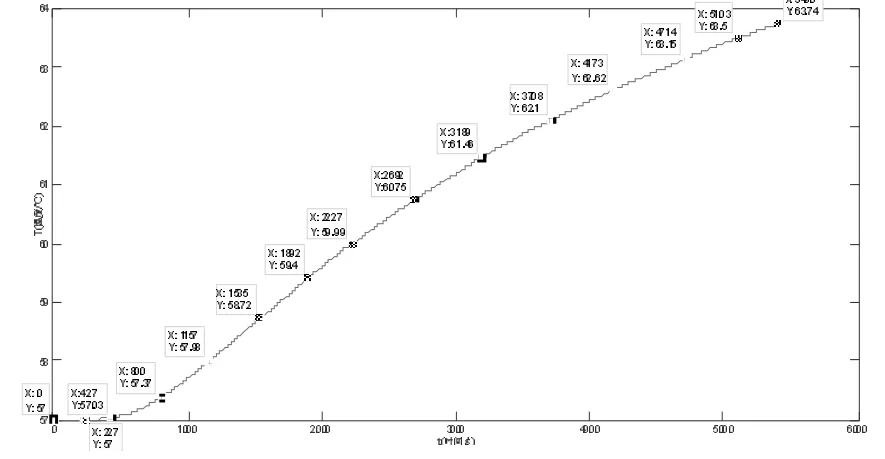
图3 第I 层中心坐标处温度分布

3 结论

据图同理也可得到，第II、III、IV 层的温度分布三维图和材料层中心坐标处温度分布数据图，在此不再赘述。由上述图表就可以清晰地知道各个位置的温度分布规律。由结果可知，传热90 分钟后，第I 层材料的最高温度63.74℃；第II 层材料的最高温度56.37℃；第I 层材料的最高温度51.76℃；第IV 层材料的最高温度45.97℃；皮肤外侧的最高温度为48.08℃。