滞留量测量校正技术研究
周志波,刘永德,刘立坤,杨丽芳,李多宏,谭西早,武朝辉
(国家核安保技术中心,北京 102401)
在核燃料循环过程中, 特别是在散料处理设施, 如: 铀浓缩设施、 核燃料组件制造厂、 乏燃料后处理设施等, 经过长期运行,会有一定数量的核材料残留在工艺设备和管道中, 这些残留的核材料通常被称之为滞留量。 它给核设施核材料衡算、 相关设备的退役、 放射性废物处理处置、 临界安全等都带来不少问题[1-2]。
国际上滞留量测量通常可分为无源γ 能谱技术和无源中子计数计数两类。其中无源γ能谱技术使用比较广泛, 对于铀、 钚核材料的测量都能适用。 该方法采用不同的数学模型来近似描述滞留量分布, 通过刻度的方法求出探测器对不同分布的滞留量的探测效率,进而求得工艺设备和管道中的滞留量的值。但因目前使用的数学模型只有点、 线、 面模型, 只能较粗的反应核材料的残留情况, 当核材料的实际残留情况与数学模型存在较大差异时,分析结果会存在较大误差[3-9]。
基于此, 介绍一种滞留量测量的校正方法。 该方法在点模型和线模型的基础上提出两种校正模型, 当核材料残留呈线状分布但存在一定宽度或呈点状分布但存在一定面积时, 提出的校正方法能对滞留量的测量结果起到较好的修正效果。
1 γ 能谱法滞留量分析原理
γ 能谱法滞留量测试系统基于γ 射线无损测量装置,装置采用NaI 探测器。其具体方法是: 首先使用γ 探测器沿工艺设备或管道测量,探测设备或管道中的热点(γ 计数率较大的地方), 然后根据热点的分布情况, 采用不同的数学模型(如点、 线、 面模型)来近似描述滞留量分布,进而求得工艺设备和管道中残留的核材料量[10]。 测量示意图如图1所示。
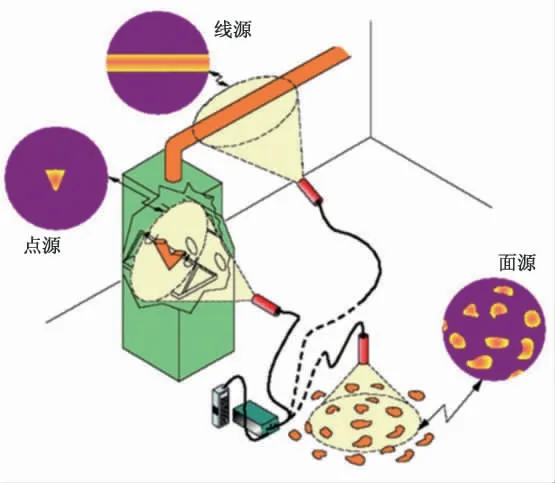
图1 滞留量测量示意图Fig.1 Schematic diagram of holdup measurement
1.1 点源模型

图2 点源模型示意图Fig.2 Schematic diagram of point source model
如图2 所示, 点源的测量模型, 如果待测滞留量的外径尺寸远小于测试距离时, 则可以简化成点源进行测试, 如管道直角处、泵头部位、 阀门部位可用点源模型。 探测器的净峰计数率Cs(如235U 的185.72 keVγ 射线净峰计数率, 以下同)与滞留量m0(235U 的质量,以下同)的关系可由公式1 表示:

式中:Kp—刻度系数,g·s·cm-2;d0—距离,cm;CF—射线的吸收校正因子。 利用标准点源通过实验可以得到刻度系数Kp(刻度时,点源自吸收效应较小,CF 近似为1)。

式中:m0—刻度实验时使用的标准点源的235U的质量;d0—刻度时探测器距点源的距离。
进而可以得到实际滞留量测量时, 待测样品的滞留量为:

式中:C(d)—现场测试的特征γ 射线净峰计数率;d—实际测量时探测器与被测物项的距离;CF—射线的吸收校正因子(实际测量过程中, 核材料发射的特征γ 射线, 会因为核材料自身、 管壁或容器壁的吸收效应而导致衰减, 吸收校正因子为核材料发射的特征γ 射线计数率与经衰减后的特征γ 射线计数率的比值)。
1.2 线源模型
理想的线源如图3 所示。 管道内的滞留量, 它的分布是连续的, 当伽马探头距离管道d0距离时,探测器视场内一定长度的管道,每个位置与探头的相对距离不一样, 因此探测效率也不一样, 管道内滞留量可以利用线源进行刻度。
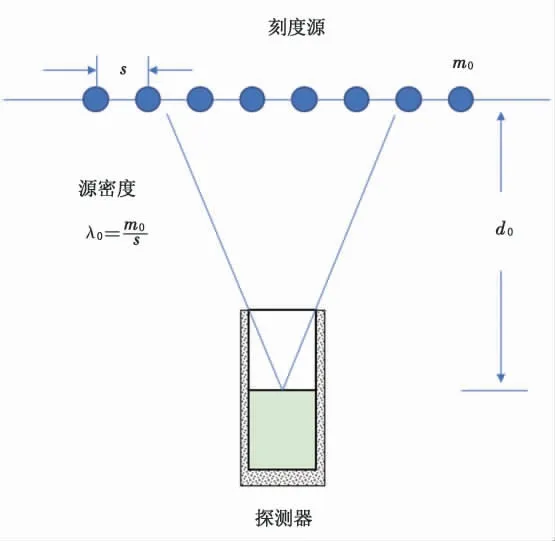
图3 线源模型示意图Fig.3 Schematic diagram of line source model
测量线源时,探测器的净峰计数率Cλ与滞留量线密度λ 的关系可利用公式4 表示。

如果没有标准的线源, 可利用点源来模拟线源, 利用不同位置时点源的探测效率来计算线源的探测效率。 如图3 所示, 点源测量位置等距离分布,点间距s 趋近零时就是标准线源, 而实际刻度测量时总会选择一个合适的间距。 刻度测量时, 点源自吸收效应较小,CF 近似为1, 刻度使用点源235U 的质量为m0,此时模拟的线源的线密度为:λ=m0/s,刻度系数KL可有式(5)计算得到:

式中:d0—刻度时探测器距线源的距离;Cλ—图3 中探测器视野范围内不同测量位置时,各点源的净峰计数率之和。
得到刻度系数KL以后,实际测量时,线源滞留量的线密度计算公式为:

式中:C(d)—现场测试的特征γ 射线净峰计数率;d—实际测量时探测器与被测物项的距离;CF—射线的吸收校正因子。
1.3 面源模型
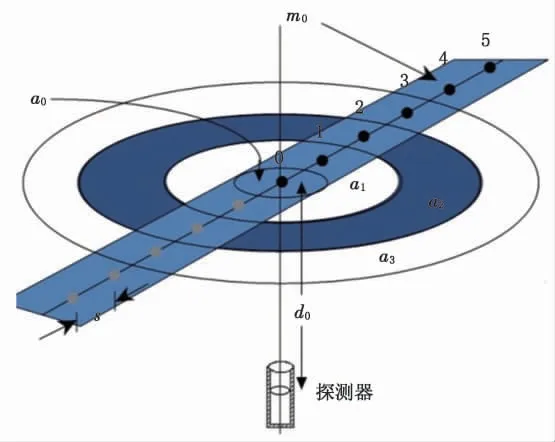
图4 面源模型示意图Fig.4 Schematic diagram of area source model
当待测滞留量呈面分布, 且其面积相对探测器视野范围足够大时, 可采用面模型进行分析, 伽马探测器距离面源距离为d0时(图4), 探测器视场内一定面积的滞留量分布, 每个位置与探头的相对距离不一样, 因此探测效率也不一样, 面分布内滞留量可以利用面源进行刻度。 测量面源时, 探测器的净峰计数率Cρ与滞留量面密度ρ 的关系可利用公式7 表示:

如果没有标准的面源, 可利用点源来模拟面源, 利用不同位置时点源的探测效率来计算面源的探测效率。 如图4 所示, 放射源的分布与测量方式和线源类似 (相邻两个测量点间的距离为s), 但因不同位置点源对应的面积不一致, 因此对不同位置的计数率需乘一个与面积相关的权重因子, 点源在中心点时 (位置0),对应的面积为πs2/4,面源面密度为ρ=m0/(πs2/4),在位置i 时,对应的面积为:
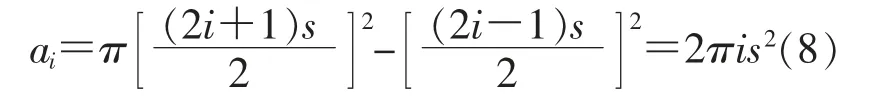
为了使面源的面密度保持与中心,位置i的点源强度应该为位置0 时倍,而实际测量时用的是同一个点源,因此,位置i 的计数率需乘以权重因子由式(8)可得:
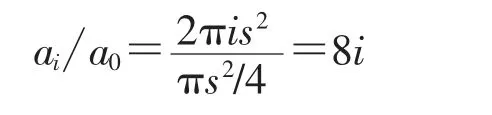

代入式(7)可得刻度系数KA为:

式中:C0—点源在探测器正前方,与探测器距离为d0时(图4),测量得到的计数率;Ci—其他不同测试点的计数率, 相邻测量点间的间距为s。
得到刻度系数KL以后,实际测量时,面源滞留量的面密度计算公式为:

式中:C(d)—现场测试的特征γ 射线净峰计数率;d—实际测量时探测器与被测物项的距离;CF—射线的吸收校正因子。
2 滞留量点、线模型校正分析方法
在实际滞留量测量过程中, 由于残留核材料的分布与使用的数学模型之间存在较大的差异, 导致分析结果与实际残留核材料的量偏差较大。 当使用点模型时, 如果残留的核材料的分布面积较大, 就会因为边缘与中心分布的核材料的探测效率不一致, 导致分析结果出现偏差; 同样在使用线模型时, 如果残留的核材料的分布宽度较大, 也会因为探测效率的变化带来结果的偏差, 为此, 提出针对这两种数学模型的修正方法。
当滞留量分布为理想的点模型时, 探测器对滞留量的探测效率为点源正对探测器,探测距离为r0时的探测效率,r0为滞留量测量时探测器前表面距离核材料残留位置的距离(图5)。
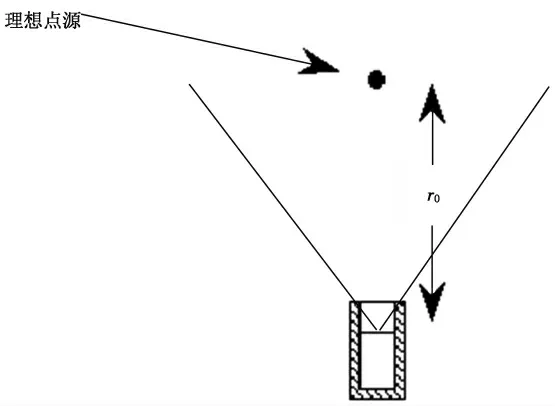
图5 理想的点模型Fig.5 Ideal point model
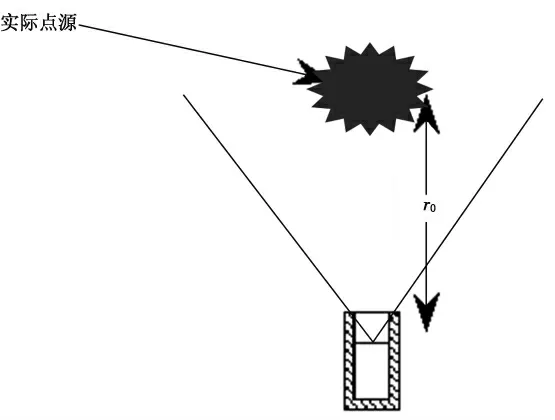
图6 存在一定面积的点模型Fig.6 Point model with a certain area
然而, 当滞留量分布存在一定的面积时(图6),如果仍用第1.1 节中的点模型分析方法, 则会导致分析结果偏低, 因为此时滞留量中心点的效率与刻度时的效率一致, 而偏离中心点的其他位置效率都比中心点的效率低, 随着滞留量分布面积的增大, 越远离中心点的地方, 探测效率越低。 因此, 必须使用实际点源的平均探测效率对第1.1 节中的计算公式进行修正。
同理, 当滞留量分布为存在一定宽度的线模型时(图7),如果采用第1.2 节中的线源分析方法, 也会导致分析结果偏低, 因为线源中轴线上的探测效率与刻度时的探测效率一致, 而偏离中轴线位置的探测效率会比刻度时的探测效率偏低,随着线源宽度的增大,越偏离中轴线位置的探测效率越低, 因此,必须使用实际线源的平均探测效率对第1.2 节中的计算公式进行修正。

图7 探测器对宽线源探测效率的变化Fig.7 Change of detector efficiency for wide line source
点源、线源修正算法具体如下:1)假设进行点源、 线源刻度时放射源距离探测器表面的垂直距离为d0, 在距离探测器表面d0,垂直于探测器轴线的位置上(图8),移动放射源可以得到探测器探测效率的径向分布曲线如图9。

图8 放射源摆放位置Fig.8 Placement of radioactive sources

图9 探测器探测效率的径向分布曲线Fig.9 Radial distribution curve of detector efficiency
用多项式拟合探测器探测效率的径向分布曲线,得:

式中:η—探测器的探测效率;l—放射源到探测器轴线的距离,cm;a1,a2,a3,a4,a5—拟合参数。
2)实际测量时,点源、线源的展宽为w,探测器距点源、线源中心距离为d,定义有效探测效率ηeff:

3)点源、线源修正因子:
点源修正因子CFP=ηeff-2, 线源修正因子CFL=ηeff-1。
对式(3)经修正后,可以得到实际测量时宽度为d 的点源滞留量计算公式为:
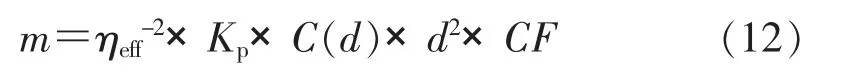
式中:C(d)—现场测试的特征γ 射线净峰计数率;Kp—点源刻度系数;d—实际测量时探测器与被测物项的距离,cm;CF—射线的吸收校正因子。
对式(6)经修正后,可以得到实际测量时宽度为d 的线源滞留量的线密度计算公式为:

式中:C(d)—现场测试的特征γ 射线净峰计数率;KL—线源刻度系数;d—实际测量时探测器与被测物项的距离,cm;CF—射线的吸收校正因子。
3 实验及结果
3.1 探测器探测效率径向分布
由第2 节所叙述的分析方法可知, 要修正点、 线模型的计算结果, 首先需获得滞留量测量所用探测器对γ 射线探测效率的径向分布。为此,进行了如下实验(图10)。

图10 探测器探测效率径向分布实验装置图Fig.10 Experimental setup of radial distribution of detector detection efficiency
1)将铀源(φ5 mm×5 mm)放在放射源固定装置(图10 中的白色立方体)的中心位置,NaI 探测器放到V 型槽内,连接探测器及多道计数器, 并固定NaI 探测器在T 型支架上的位置 (探测器前表面距T 型支架横向支架中心位置的距离为50 cm);2)将放射源固定装置移至T 型支架的中心位置,测量铀源特征γ射线计数率(185.72 keV);3)保持探测器位置不变, 逐步向右平移放射源固定装置, 每隔5 cm 设置一个测量点,记录铀源特征γ 射线计数率(185.72 keV);4)使用高斯函数拟合测量数据,得到NaI 探测器探测效率径向分布的拟合函数。
该实验选用的 NaI 探测器型号为EFC100232, 晶体尺寸为2.54 cm×2.54 cm。探测器探测效率径向分布的实验数据如表1。
使用多项式:
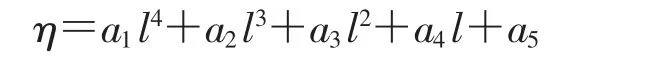
拟合探测器探测效率径向分布η 随点源距探测器轴线距离l 的关系得到图11 所示曲线。
由此,50 cm 处该探测器的探测效率径向分布如下。

表1 探测器探测效率径向分布实验数据Table 1 experimental data of radial distribution of detector detection efficiency
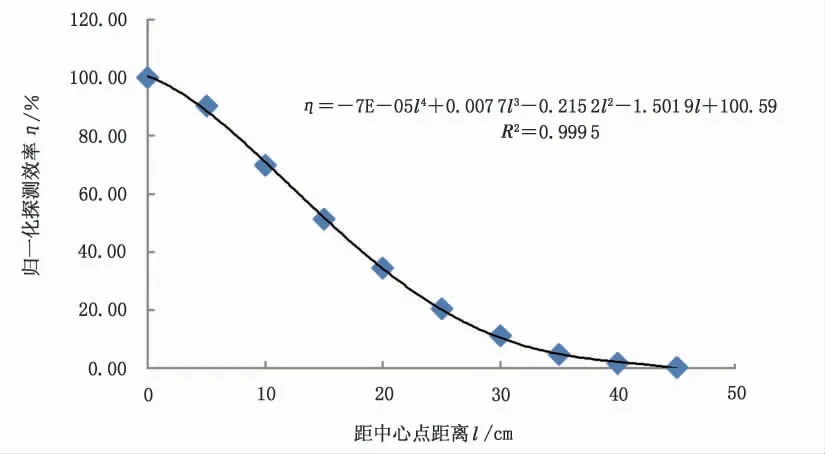
图11 探测器探测效率径向分布图Fig.11 Radial distribution of detector detection efficiency
η50cm=-7×10-5l4+0.007 7l3-0.215 2l2-1.501 9l+100.590 0
3.2 修正后的点、线模型分析结果
为了检验提出的点源、 线源修正算法的准确性,采用富集度为4.5%低浓铀粉末制作了一系列不同尺寸的点源和线源模拟样品,其具体尺寸及样品中含235U 的质量如表2 所示。
实验时, 将1-6 号模拟样品放在实验桌面上,探测器距离模拟样品距离为50 cm,实验结果如表3 所示。
实验时, 将7-13 号模拟样品放到厚1 mm、 长1 m 的聚乙烯管道, 探测器距离模拟样品距离为50 cm, 实验结果如表4所示。
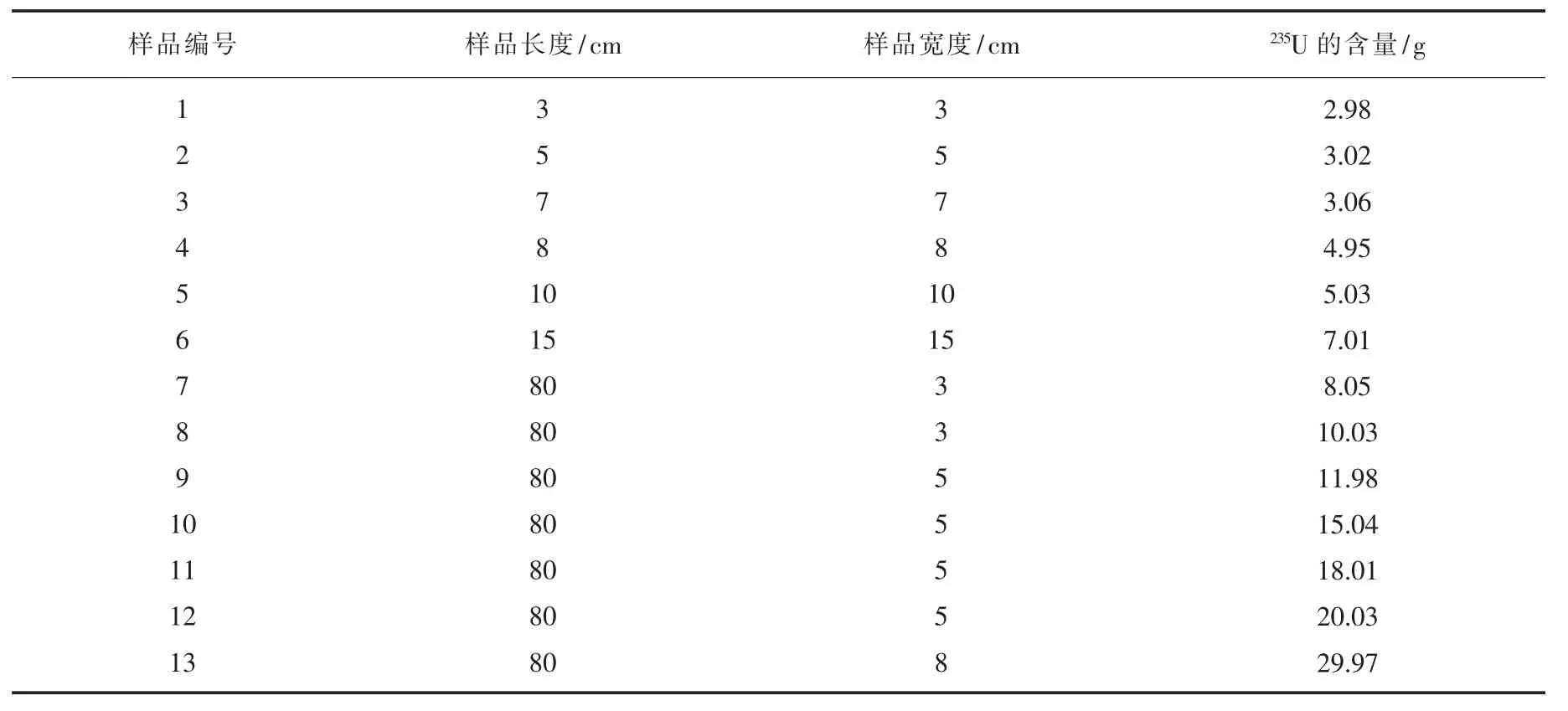
表2 模拟样品尺寸及235U 含量Table 2 Simulated sample size and 235U content
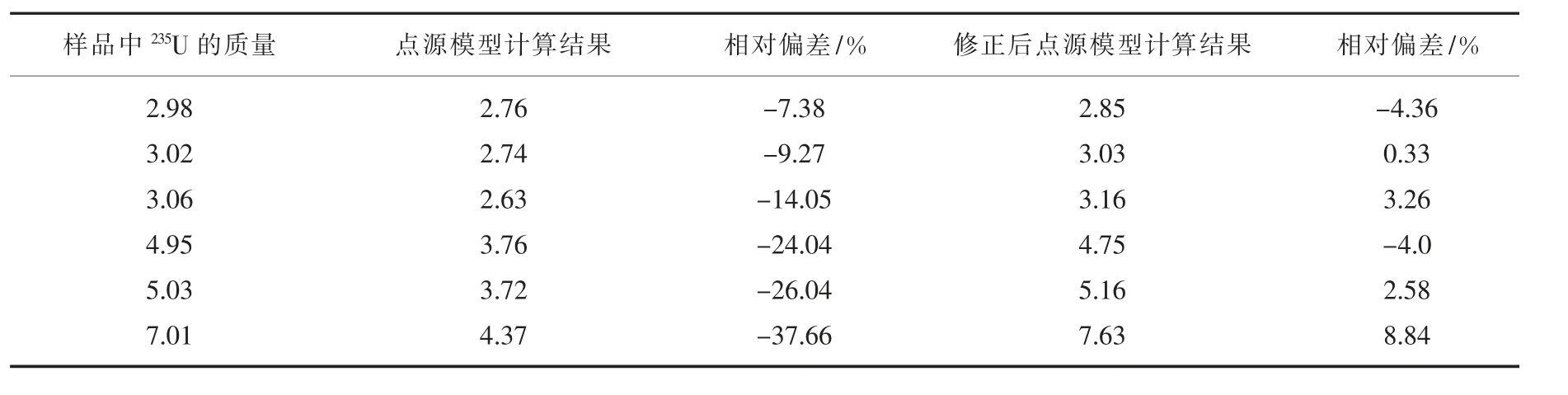
表3 点源模拟样品实验结果Table 3 Experimental results of point source simulation samples

表4 线源模拟样品实验结果Table 4 Experimental results of line source simulation samples
4 结论
讨论了一种滞留量测量的校正方法, 具体分析了当滞留量测量过程中使用点、 线模型分析时, 如果被测核材料存在一定展宽,分析结果会出现偏低的现象, 提出了一种探测效率校正方法, 并采用不同尺寸的滞留量分布进行了实验验证, 证明了该方法的可行性。 从验证实验结果看出, 未经校正的结果偏低,展宽越大,偏低越明显,经过校正后,实验结果的偏差总体减小, 分析得到的核材料的质量与标称值之间的相对偏差好于10%,实现了滞留量测量时, 因实际样品展宽导致分析结果偏低的有效校正。

