矩阵变换器的建模与仿真

王刚

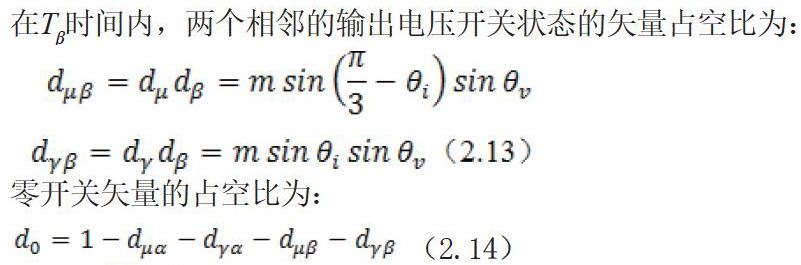
摘 要：由于矩阵变换器在体积、重量等方面具有一定的优势，它被视为是一种能够代替传统AC-DC-AC变频器的选择，在众多的电力变换场合得到了应用。文章依据空间矢量调制算法，使用Matlab/Simulink仿真，验证了控制策略的正确性。

关键词：矩阵变换器;空间矢量调制;仿真

1 引言

矩阵变换器以其简单的拓扑结构及诸多理想的电气特性，使其具有巨大的理论研究价值和广阔的应用前景，越來越受到广大研究人员的青睐，成为20世纪80年代以来的第三个交流电力变换器平台。因其具有优良的输入输出特性，并具有广义的变换器特性，使得它在众多的电力变换场合得到了应用。

本文依据双空间矢量调制算法，应用Matlab/Simulink 建立了数学模型进行计算机仿真。

2 双空间矢量调制算法

双空间矢量调制算法是一种间接调制算法，它的基础是PWM调制技术，是对矩阵变换器等效交-直-交结构的前级虚拟整流级和后级虚拟逆变级分别采用空间矢量调制技术，再将两部分有机的结合起来，实现整体控制。

2.1 空间矢量的合成原理

空间矢量的旋转角频率即为三相对称交流量的角频率，而且从式（2.1）的计算得到旋转矢量的幅值|F|正好等于三相对称交流量的幅值Fm。

2.2 调制算法中输入、输出空间的分析

2.2.1 输出空间

8个开关状态电压矢量有6个非零矢量u1-u6和两个零矢量u1和u7，6个非零电压开关矢量将空间平均分成6个区Ⅰ—Ⅵ，每个区间为60°。

在一个采样周期Ts内，期望输出的线电压空间矢量可以用两个相邻的开关状态矢量Uα、和一个零矢量U0来近似合成，其表达式为：

2.2.2 输入空间

假定负载为三相对称负载，虚拟逆变级的直流电流的局部平均值为恒值，为前级虚拟整流级提供恒定的输出电流。当电源电压对称，虚拟整流级的直流回路电流恒定，为后级虚拟逆变级供电。

2.3 空间矢量合成

以I1与U1所对应的开关组合为例，在Tα时间内，两个相邻的输出电压开关状态的矢量占空比为：

3 矩阵变换器的仿真

为了验证本章理论分析和推导的正确性，应用Matlab/Simulink 建立了数学模型进行计算机仿真。

仿真目的：1）验证提出的调制策略的正确性，主要是看输出电压和输入电流的波形质量。2）带不平衡负载时，观察输入电流的变化。

仿真系统参数如下：输入电压频率100Hz;输入相电压幅值145V;三相负载电感1mH;三相负载电阻2Ω;输出电压频率50Hz;输出相电压幅值220V。

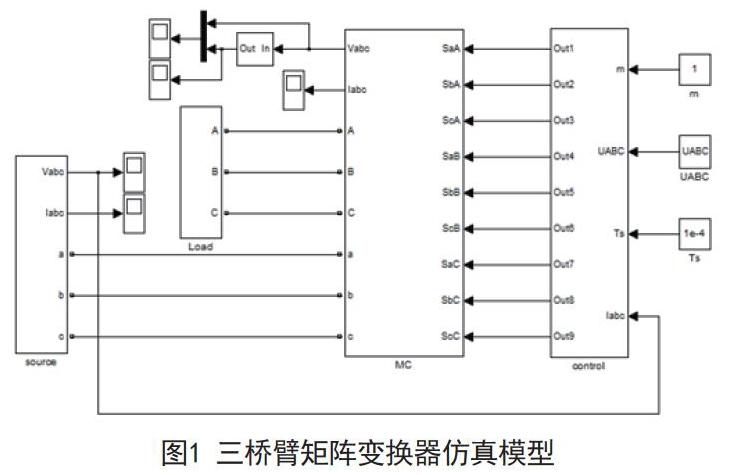
采用Matlab＼Simulink作为仿真工具，主要包括五个模块：开关矩阵模块（MC）、控制模块（control）、负载模块（Load）、给定电压模块（source）、和测量模块，如图1所示。

开关矩阵模块由9个理想开关组成。根据空间矢量调制算法，控制模块分为角度计算、扇区判断、占空比计算和开关控制等四个子模块。角度计算模块包括输入电流角度和输出电压角度的计算。占空比计算是根据I和U所处扇区和扇区角通过公式（2-6）（2-11）（2-14）求得。根据Park方程和前面计算，控制开关矩阵的动作。

仿真分析：输出电压波形和电流波形如图2所示，输入电流波形如图3所示。

从图中可以看到，输出电压波形和输入电流波形均为比较规则的正弦波，与期望的波形基本一致，验证了模型的有效性。

4 小结

本文对矩阵变换器的拓扑和工作原理进行了分析，介绍了双空间矢量合成的基本原理，对调制算法中输入空间和输出空间进行详细说明，并推导了整流级和逆变级占空比表达式，得到3×3矩阵变换器的调制策略。带平衡负载时，通过仿真验证了本章理论分析的正确性。

参考文献

[1]邓文浪，杨欣荣，朱建林，等.无功功率可控的双级矩阵变换器空间矢量调制策略[J].电力系统自动化，2005，29（18）：33-38.

[2]陈希有，陈学允.矩阵式电力变换器的无功功率分析[J].中国电机工程学报，1999，19（11）：5-9.

[3]李嘉杰，杨俊华，王孝洪，等.无刷双馈风力发电系统的矩阵变换器励磁控制[J].高电压技术，2009，35（8）：2024-2029.

[4]邓文浪，杨欣荣，朱建林，等.矩阵变换器双空间矢量调制简化算法的研究[J].电气传动，2006，36（7）：43-47.

[5]李志勇，朱建林，易灵芝，等.空间矢量调制的矩阵式变换器仿真模型研究[J].中国电机工程学报，2003，23（3）：80-84.