高温气冷堆石墨构件的碰撞力学行为研究

祁志伟，王晓欣，史 力，王洪涛，孙立斌

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

高温气冷堆(HTGR)和熔盐堆(MSR)通常采用石墨和碳砖作为慢化剂和反射层，这些部件同时也是堆芯的支承结构，对核电站的安全至关重要。由于石墨是脆性材料，成品尺寸较小，反应堆中一般采用堆砌结构，砖与砖之间设有间隙，并通过石墨方键或圆榫来连接相邻的砖块。由于间隙的存在，石墨砖在动态激励下会表现出非线性特征[1-4]。为研究这种大规模散体结构的动力特性，在过去的几十年中针对棱柱式和球床式高温气冷堆两种类型已开展了许多振动台实验和数值分析[1,4-10]。振动台实验由于实验台尺寸的限制，只能对部分构件或采用缩比模型进行测试，不能完全反映堆内石墨构件的动力特性。因此，数值分析是高温气冷堆堆内构件在地震载荷下安全性评价最为重要的方法。

山东石岛湾200 MW球床模块式高温气冷堆(HTR-PM)堆内构件包含的石墨砖或碳砖超过3 000个，方键或圆榫超过1万个。采用细致的三维模型并考虑接触和摩擦等碰撞特性的经典有限元方法对计算机要求非常高，且对结果的后处理非常困难，因此一系列简化方法已被开发用于多种数值程序，如用于先进型气冷堆的AGRCOR[11]，棱柱型HTGR的AGRCORUK7、CRUNCH-10、CRUNCH-20、MCOCO和GTOROTO等程序[1,12-14]。这些模型中砖块被视为刚体质点，通过使用非线性连接器连接两个刚体质点来模拟两个构件间的相互作用，极大简化了碰撞问题，提高了计算效率。数值模型的动态响应主要取决于连接器的刚度和阻尼，这些参数的合理性对于数值分析的准确性十分重要。

HTGR的石墨砖通过方键和圆榫进行连接，砖与砖之间主要有3种碰撞类型，为获得这些典型碰撞形式下的连接单元属性，本文对3种碰撞类型的实验进行数值分析，通过实验和数值分析得到的碰撞时间和恢复系数计算不同碰撞速度下Hertz模型的等效刚度系数和等效阻尼系数，并进一步研究碰撞间隙以及石墨砖质量对碰撞的影响。

1 碰撞实验

为研究不同碰撞类型的动态行为，开展了3组实验，分别为砖-砖、砖-圆榫与砖-方键碰撞实验，其中第1组实验(砖-砖碰撞)结果详见文献[15]。第2、3组实验中，采用同样尺寸的石墨砖放置于平行的轨道上，在待碰砖侧面设置榫槽或键槽，主动碰撞砖块沿相同的轨道以不同的速度撞向待碰砖块，示意图如图1a、b所示。每组进行约130次碰撞实验，碰撞速度在0.1～2.4 m/s之间。测量方式采用光学方法，在石墨砖表面制作一系列标记点，由高速摄像机拍摄极短时间内石墨翻转的图像，利用灰度重心法和二值法对标记点进行处理，得出各点的灰度重心坐标，进而获得砖块在碰撞过程中的位移情况，计算碰撞速度[15]。由于碰撞和待碰石墨砖均未固定在轨道上，因此无法测量碰撞过程中的相互作用力。

实验件采用各项同性的石墨材料NG-CT-01(成都炭素有限责任公司)，其性质与HTGR中的IG110型号石墨类似，两种材料的特性参数列于表1[16]。

a——第2组碰撞实验；b——第3组碰撞实验；c——第2组碰撞数值模型；d——第3组碰撞数值模型红色：主动碰撞试件；绿色：待碰试件；蓝色：键和榫图1 碰撞实验及数值模型示意图Fig.1 Layout of collision test and numerical model

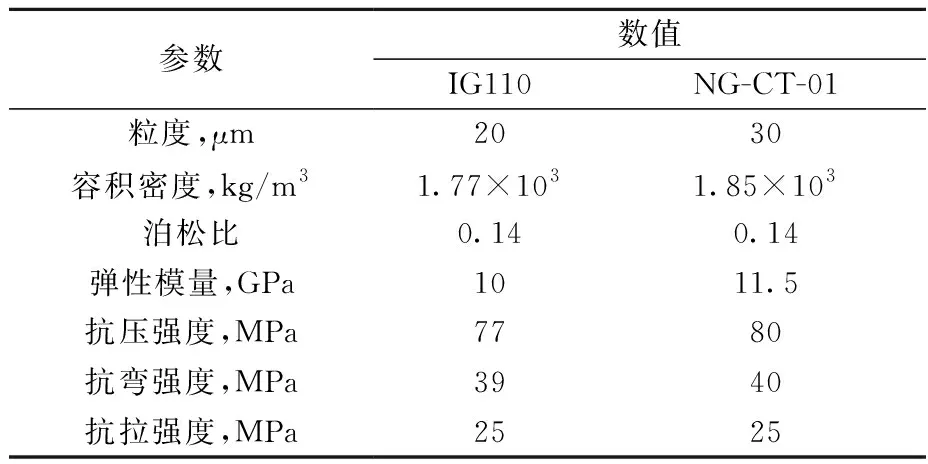
表1 石墨材料的主要特性参数Table 1 Main property parameter of graphite material

3组砖块不同碰撞类型的典型速度曲线示于图2。第1组速度曲线与经典碰撞模型的趋势一致[16]，碰撞过程中两块砖之间的相对速度以相同的梯度急剧变化，可很容易地获得碰撞时间和恢复系数。

第2、3组速度曲线与第1组差异较大，其碰撞时间约为100 ms，明显大于第1组的2 ms，此外碰撞过程中速度曲线的斜率在图2b中并不恒定。碰撞接触开始时试件速度迅速改变，速度的斜率也在逐渐减小，直到石墨砖的速度保持恒定。实验期间观测到石墨砖的旋转，原因可能是轨道的刚度不够大，圆榫和石墨砖在碰撞过程中发生翻转，导致了碰撞时间增加。尽管发生了翻转，石墨砖速度的主要方向仍未发生变化，通过第2、3组碰撞实验获取的恢复系数可用于表示能量耗散机制，如图3所示。第2、3组的恢复系数更为分散，变化趋势也有所不同。恢复系数在碰撞速度为0～0.6 m/s时随碰撞速度的增大而增大，在0.6～1.2 m/s时随碰撞速度的增大而减小。

图2 典型速度曲线Fig.2 Typical velocity curve

2 数值分析

第2、3组实验的碰撞时间受到石墨砖翻转的影响，但在实际反应堆中，石墨构件在竖直方向上有50层，上面还有其他限位构件，石墨砖围绕水平轴的翻转并不会发生，因此第2、3组实验并不能代表反应堆中的实际情况。当采用合适的模型和材料参数时，有限元可合理分析石墨的碰撞行为，这在第1组实验结果和有限元分析结果的对比中已得到了论证[15]。为进一步研究更复杂碰撞机制下的碰撞时间，本文使用商业有限元软件ABAQUS来模拟上述两组碰撞实验。考虑到碰撞试件的几何形状和边界条件的对称性，为简化计算过程，采用1/2模型进行模拟，以竖直方向的中面作为对称面，与砖块底面轨道相连节点受到x方向上的位移约束。在这种约束条件下，石墨本身不会发生翻转，但在键榫与砖的间隙会导致键榫的轻微翻转，与堆内实际情况相同。方键与砖之间的接触设置为摩擦系数0.2的滑动摩擦[3]。通过网格敏感性分析后确定的有限元模型和网格划分如图1c、d所示。石墨材料特性参见文献[16-17]。

图3 第2、3组实验中恢复系数与碰撞速度的关系Fig.3 Restitution coefficient of collision test in group 2 and 3

分析中采用Rayleigh阻尼，其阻尼矩阵C定义如下：

C=αM+βK

(1)

其中：M为模型的质量矩阵；K为模型的刚度矩阵；α和β分别为每个矩阵的独立因子。对于细级核石墨，文献[17]建议使用以下α和β表达式：

α=15.0β=5×10-5(v0/v)2

(2)

其中：v0=1.0 m/s为碰撞参考速度；v为石墨砖碰撞相对初始速度。

初步分析发现，采用上述表达式时阻尼系数的数值分析结果与实验结果有较大差距，这主要是由于砖与圆榫和方键碰撞的过程中接触面积、应力水平与正碰实验差别明显。考虑到实验中的恢复系数可代表实际碰撞，而β的影响更为显著，因此对模拟过程中的β进行修改拟合，获取与实验结果相符的恢复系数，得出两组实验的阻尼系数β，如表2所列。

表2 数值分析得出的Rayleigh 阻尼系数β和碰撞时间tTable 2 Rayleigh damping coefficient β and collision time t in numerical analysis

使用有限元分析获得的第2、3组实验的典型速度曲线如图4所示。与图2b相比未观察到砖的翻转，此外，曲线的斜率在碰撞过程中呈梯度变化，这表明方键和圆榫的翻转不明显，因此模拟得出的碰撞时间可用于表示砖与方键或圆榫的实际碰撞时间，不同碰撞速度下的碰撞时间列于表2。

3 间隙及附加质量的影响

反应堆设计中，石墨砖的尺寸和部件之间的间隙是结构优化的主要内容，另外石墨在中子的辐照作用下可能发生体积收缩和膨胀[18]，为研究这些设计参数变化对石墨砖碰撞性能的影响，通过上述数值模拟得出砖-圆榫、砖-方键数值模型中修正的阻尼系数，进一步探索碰撞间隙及附加质量对碰撞过程的影响。

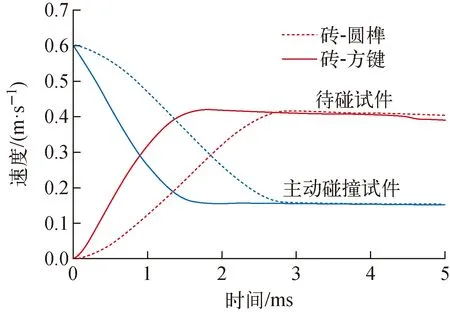
图4 第2、3组实验数值模型的典型速度曲线Fig.4 Typical velocity curve for test in group 2 and group 3

对于砖-圆榫碰撞，通过修改圆榫的截面半径来改变碰撞间隙，分别设置了8组(0.3、0.4、0.6、1、1.5、2、3、4 mm)不同的间隙模型。对于砖-方键碰撞，通过修改方键在速度方向的长度来改变碰撞间隙，分别设置了7组(0.35、0.5、1、1.5、2、2.5、3 mm)不同的间隙模型。分别模拟碰撞速度在0.3、0.45、0.6、0.75、0.9 m/s下不同间隙的碰撞情况。砖-圆榫碰撞的恢复系数和碰撞时间与碰撞间隙的关系如图5所示。随着碰撞间隙的增加，石墨砖碰撞的恢复系数逐渐减小，碰撞时间不断增加，这主要归因于间隙增大使得圆榫的翻转现象更加明显。对于砖-方键碰撞，随着间隙的增大，其恢复系数和碰撞时间并无明显变化，主要原因是方键在碰撞过程中接触面积较大且翻转并不明显，即使在一定范围内增大碰撞间隙，也不会导致碰撞情况的改变。

通过在砖块模型上附加无结构质量，进而改变碰撞模型的质量，以此研究相同榫键结构下，石墨砖质量对碰撞参数的影响。附加质量选取7组(0、0.1、0.3、0.6、1、1.5、2)不同因子(附加质量/自重)进行不同碰撞速度下的数值分析。砖-圆榫和砖-方键碰撞的恢复系数和碰撞时间与附加质量的关系如图6所示。随附加质量的增加，砖-圆榫碰撞的恢复系数减小，砖-方键碰撞的恢复系数增加，两种类型的碰撞时间均随附加质量而增大。

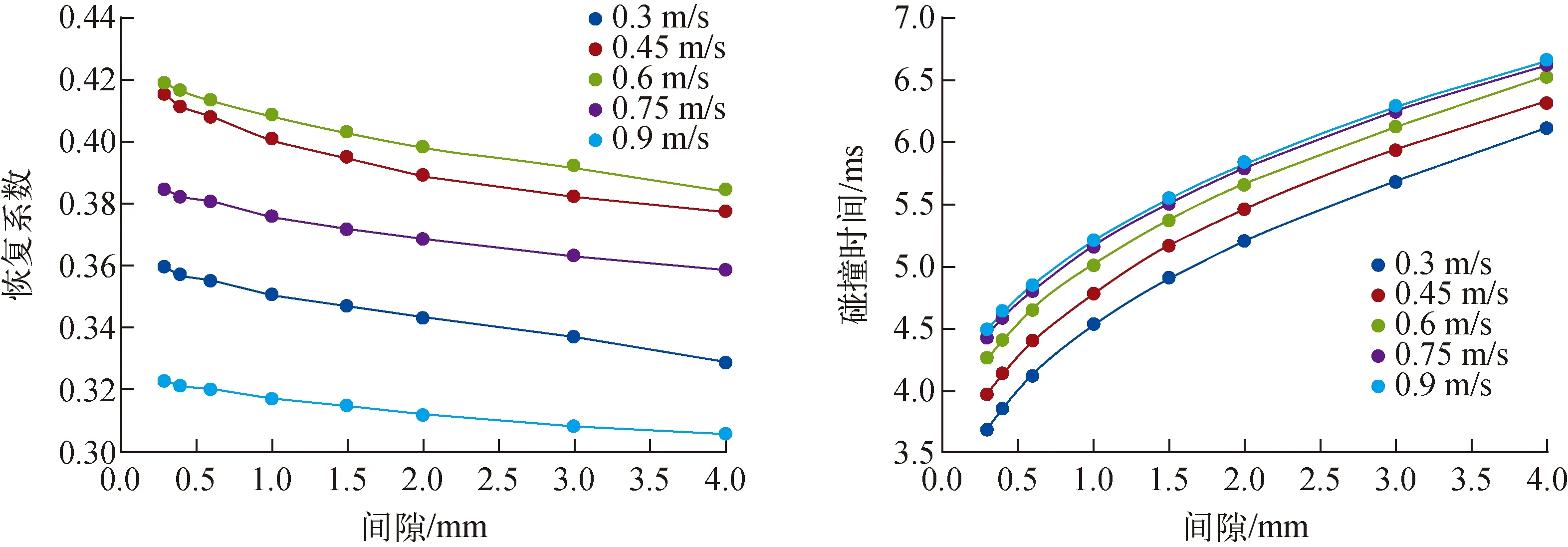
图5 砖-圆榫碰撞恢复系数和碰撞时间与碰撞间隙的关系Fig.5 Restitution coefficient and collision time with different gaps in brick-dowel contact

图6 砖-圆榫和砖-方键碰撞恢复系数和碰撞时间与附加质量的关系Fig.6 Restitution coefficient and collision time with additional mass in brick-dowel and brick-key contacts

4 Hertz模型的参数计算

根据经典的碰撞理论，接触力F和碰撞间隙之间的关系可描述为：

(3)

其中：K为等效刚度系数；C为等效阻尼系数；δ为碰撞过程中的相对位移；δ′为碰撞物体的相对速度。当n=1且m=0时，式(3)表示Kelvin-Voight模型[12]；当n=m>1时，表示Hertz模型。目前大部分反应堆石墨构件数值模型中均采用将K和δ之间假定为线性关系的Kelvin-Voight模型，该模型的K和C可通过碰撞过程中的碰撞时间和恢复系数(碰撞后和碰撞前相速度的比值)推导得到[12]，其中碰撞时间主要影响等效刚度系数K，恢复系数e则与等效阻尼系数C相关。

Kelvin-Voight模型形式简单，可较易应用到有限元分析软件中，但有一定的局限性。该模型在碰撞过程中等效阻尼系数是恒定的，且由于在碰撞开始阶段引入阻尼力，这种情况与实际不符合。相比之下，Hertz模型能更准确地表示碰撞行为，已应用于建筑物的碰撞分析[19]，然而尚未在反应堆石墨构件的动力学分析中得到应用。

方程(3)适用于球状物体的碰撞，对于砖块与圆榫的碰撞，由于接触面积较小，根据类似结构的静力实验结果，取n=m=2[3]。等效刚度系数K主要由碰撞时间确定，它随碰撞时间的增大而减小。将两个碰撞物体视为质点，可通过数值方式通过MATLAB软件对运动过程(式(3))进行求解，获得K与碰撞时间的关系，当计算的碰撞时间与第1组实验和有限元分析(第2、3组实验)中的结果相同时，该刚度即为合理的碰撞单元等效刚度。等效阻尼系数C表达式[20]如下：

(4)

其中，δ′0为碰撞的相对初始速度。根据式(1)、(4)，当K已知时，可通过实验测量得到的恢复系数来计算等效阻尼系数。

采用上述方法计算的等效刚度系数与等效阻尼系数如图7所示。

为研究间隙和附加质量对碰撞参数的影响，采用同样方法计算其等效刚度系数和等效阻尼系数，结果如图8所示。由于间隙的增大对砖-方键碰撞影响很小，因此其等效刚度系数和等效阻尼系数的曲线与图7相同。从图8可看出，随着速度的增加，等效刚度系数和等效阻尼系数逐渐减小。

图7 第2、3组碰撞实验的等效刚度系数和等效阻尼系数Fig.7 Equivalent stiffness and damping coefficients for group 2 and group 3

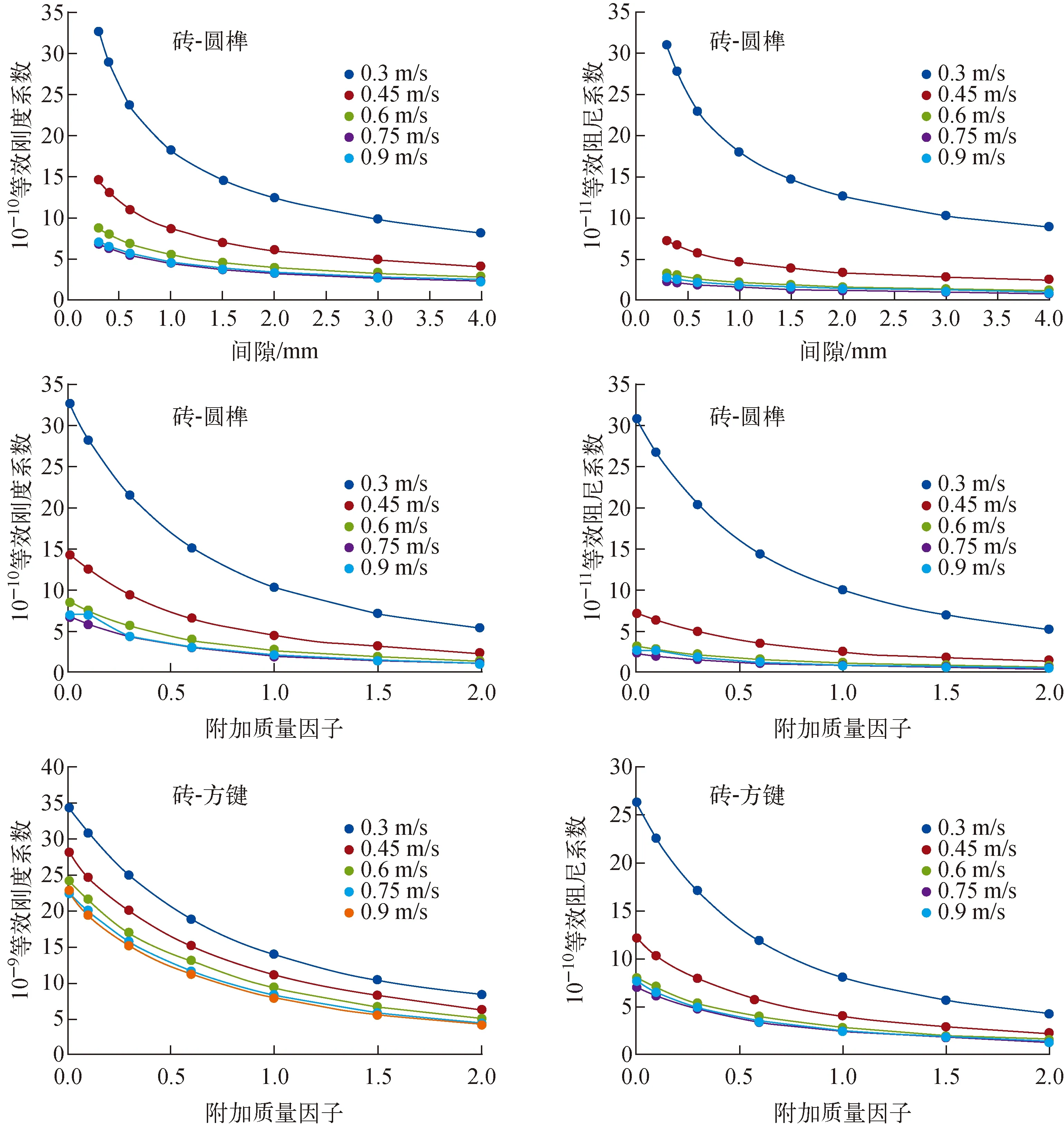
图8 不同影响因素下砖-圆榫和砖-方键碰撞实验的等效刚度系数和等效阻尼系数Fig.8 Equivalent stiffness and damping coefficients for brick-dowel and brick-key contact under different influence factors

图5、6中砖-圆榫和砖-方键的恢复系数和碰撞时间随碰撞速度的增加无明显的变化规律，然而图7、8中简化Hertz模型的等效刚度系数和等效阻尼系数均在碰撞速度较大时趋向较为稳定的值。这是由于碰撞速度较小情况下，碰撞时榫键在键槽内的翻转滑动对恢复系数和碰撞时间有明显的影响；榫键翻转后与石墨砖完全接触到位，各部件的形状位置不再发生非线性变化，结构的响应主要为线弹性变化，因此碰撞速度较大时等效刚度系数与等效阻尼系数变化不大。当间隙与石墨砖质量增加时，Hertz碰撞单元的等效刚度系数和等效阻尼系数均有所降低，碰撞速度引起的差异也逐渐减小，这些结果可直接用于高温气冷堆石墨堆内构件的动力学分析模型中，以指导石墨散体结构的设计优化。

5 结论

本文通过细颗粒核级石墨砖的碰撞实验和数值分析，获得了砖-砖、砖-圆榫和砖-方键3种不同碰撞类型的碰撞时间和恢复系数，以及砖-圆榫和砖-方键结构的材料阻尼系数。基于实验和数值分析结果，采用改进的Hertz模型计算了简化碰撞单元的等效刚度系数和等效阻尼系数。通过验证的数值模型，进一步探究了砖和连接键榫间的间隙以及砖块质量对石墨砖碰撞行为的影响，获得了不同设计条件下碰撞单元的参数。这些参数将为HTGR中石墨内部构件的地震分析和评估提供重要依据，并为其他堆型石墨堆内构件的设计与优化提供参考。