冷却剂与含格架燃料棒束多场耦合分析
马玉琢,黄 美,黄继缘,张沛健
(华北电力大学 核科学与工程学院,北京 102206)
压水堆核电厂通过冷却剂流经燃料组件进行热量交换将核裂变产生的能量带出堆芯,冷却剂的流动会对燃料组件产生冲击与振动,使组件产生位移和形变,与此同时组件结构形状和位置的改变会反过来对冷却剂的流动产生显著影响。冷却剂与燃料组件间的这种相互作用直接关系到反应堆的安全运行与核电厂的运营效率。
在构成燃料组件的燃料棒束结构中,定位格架是用于支撑堆芯燃料棒束的弹性结构构件,对燃料组件的热工和结构特性影响较大。利用计算流体力学(CFD)工具对燃料组件内单相和两相流动现象的研究已十分丰富[1-3],对组件结构与冷却剂相互作用进行的流固耦合研究也日渐增多[4-6],但目前的研究大多仅限于单向流固耦合,对涉及到结构场、温度场和流场的双向多场耦合情况研究较少。
本文采用数值模拟计算中的多场耦合分析方法对冷却剂与含格架燃料棒束进行多场耦合模拟,分析研究冷却剂与燃料组件间的热工水力特性和结构形变特性,进而为堆芯的安全分析和燃料组件的优化设计提供参考。
1 计算模型
1.1 几何模型
本文通过对实际燃料组件的适当简化,忽略对流场影响轻微的固定件,保留定位格架中的条带弹簧、刚性突起和搅混翼片,建立了总长1 050 mm的5×5燃料棒束计算域。其中:入口段长度500 mm,定位格架段长度50 mm,出口段长度500 mm。燃料棒束长1 050 mm,外径9.5 mm,栅距12.6 mm;定位格架尺寸63.4 mm×63.4 mm×38.38 mm,厚度0.425 mm,定位格架上的条带弹簧高1.4 mm,刚性突起高1.18 mm,搅混翼片高5.38 mm,弯折角度30°[7]。燃料棒束与格架的几何模型如图1所示。
1.2 网格划分
基于上述几何模型,本文在入口段与出口段使用结构化网格,格架段由于结构较为复杂选用非结构化网格;格架段与入口段和出口段间通过交界面连接,3部分共同构成混合网格,如图2所示。对网格无关性进行了验证,网格参数列于表1[8]。当单元数达到485万时,各项参数满足计算需要,综合计算能力的考虑本文选用2号网格。
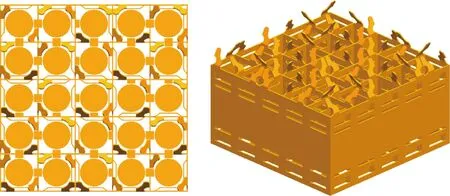
图1 棒束与格架的几何模型Fig.1 Rod and grid geometric model
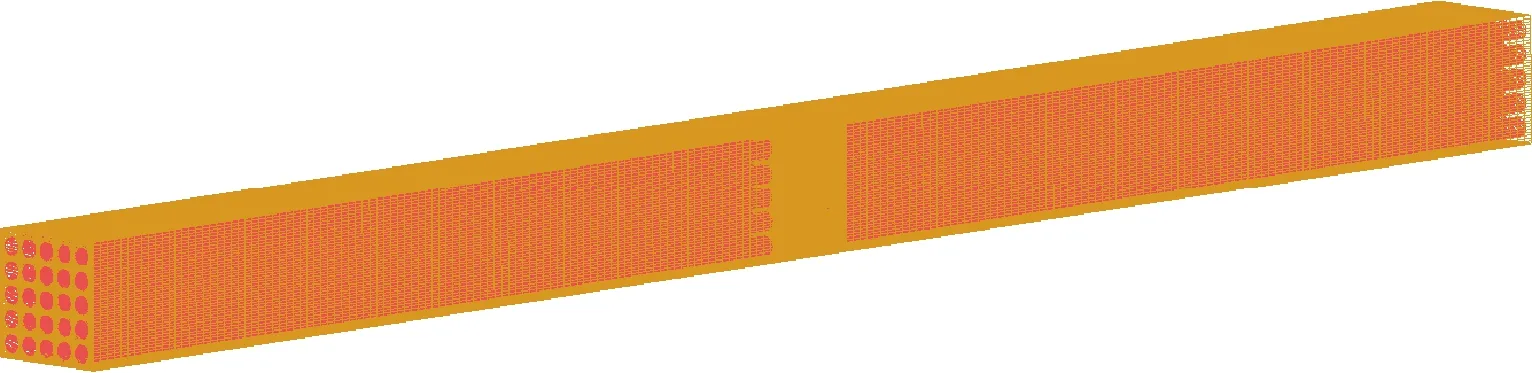
图2 混合网格结构Fig.2 Hybrid mesh structure
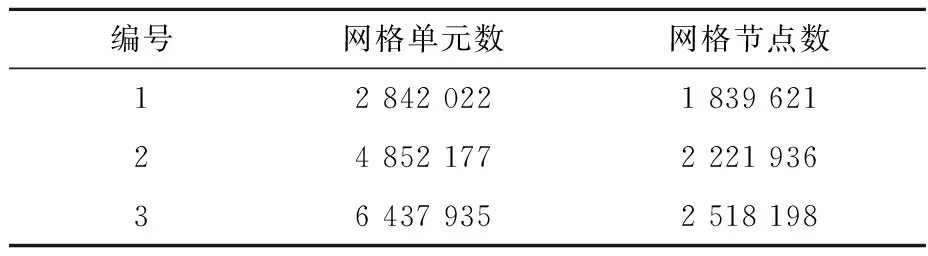
表1 网格参数统计Table 1 Mesh parameter statistics
1.3 计算条件
在带有定位格架棒束通道几何条件下,冷却剂流过定位格架附近时受壁面黏性作用,因而湍流模型对壁面处理方法的不同对模拟结果有较大影响。参考现有研究成果[9-10],对比k-ε、RNGk-ε和SSTk-ω3种湍流模型,考虑了旋流效应的SSTk-ω模型计算结果在预测压降和温度分布时更为准确,因此本文在流体计算部分采用SSTk-ω模型。
系统初始温度292 ℃,压力15.5 MPa,入口边界初速度4.8 m/s,出口为压力边界条件[11];燃料棒为粗糙壁面,根据堆芯功率密度分布特性燃料棒线热流密度沿轴向呈余弦分布[12];其他结构为无滑移、绝热固定壁面,燃料棒两端固定约束边界,定位格架为弹性约束条件。
2 数值模拟结果与分析
根据流道所在位置的不同可将冷却剂流动的子通道分为中心通道、边通道和角通道,并将燃料棒按位置分为中心棒、中层棒和外层棒。同时为便于模型对比和参数分析,分别沿燃料棒束轴向和径向选取4个截面,并在中心流道内选取一点,截面和点的位置及编号如图3所示。
2.1 数值模拟可行性验证
为验证数值模拟的可行性,选取Holloway实验布置作为模拟参数输入,模拟与实验对照如图4所示[13],结果表明归一化努塞尔数随冷却剂流动的变化趋势一致,模型能较好地模拟实际工况。
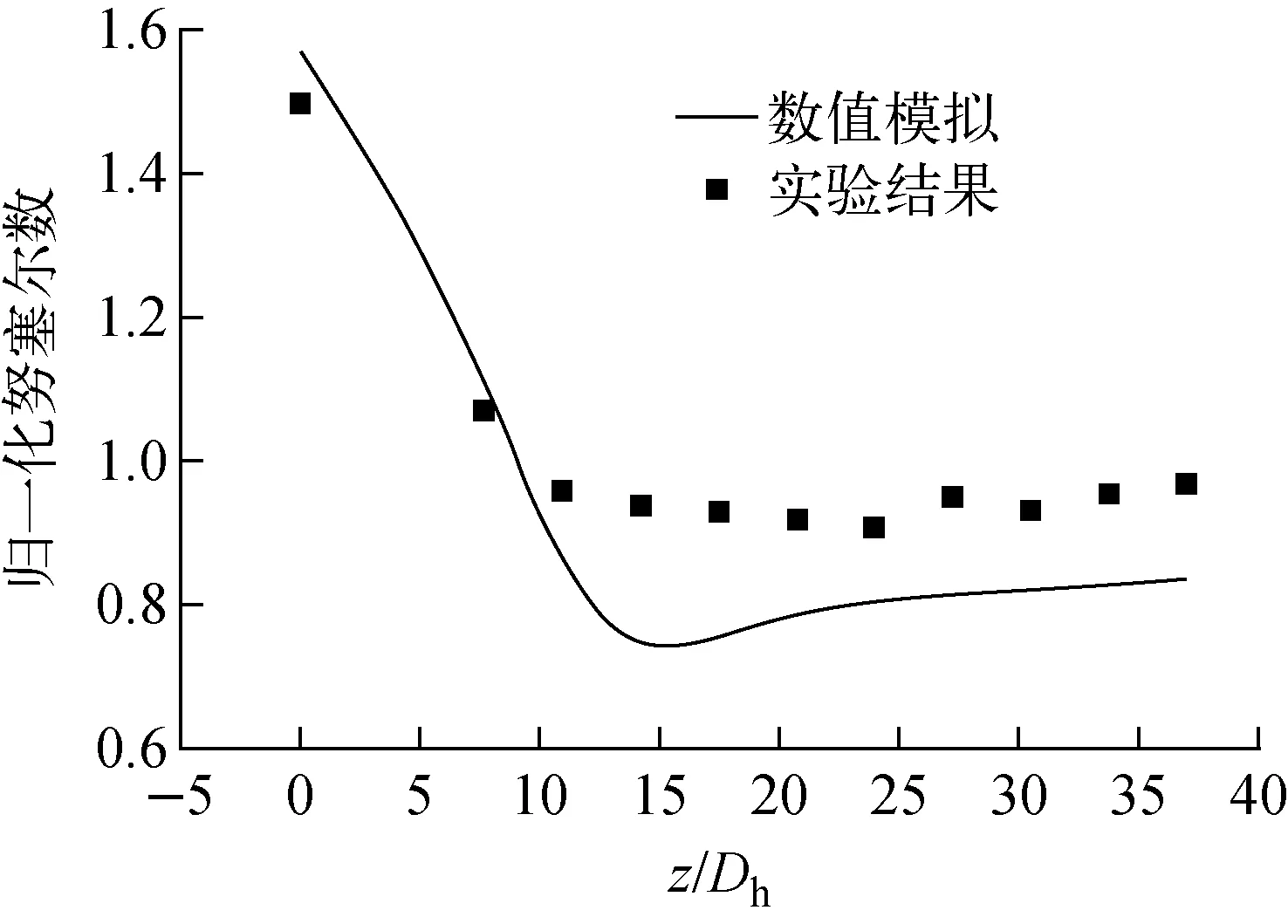
图4 数值模拟可行性验证Fig.4 Feasibility verification of numerical simulation
2.2 冷却剂流动与传热的数值模拟
对冷却剂流动与传热进行数值模拟计算,燃料棒线热流密度沿轴向呈余弦分布,平均热流密度为8.473×105W/m2,冷却剂沿燃料棒束轴向各截面(Plane1~4)上的二次流速度及温度分布云图如图5所示。由图5可见:冷却剂自下而上流动的过程中,从入口段到定位格架前几乎没有横向流动的产生,棒束与冷却剂间的换热较弱,温度梯度较大;冷却剂流入格架段后由于格架壁面、条带弹簧和刚性突起等结构的存在,开始出现流道间的横向流动,继续流动至格架出口位置,由于搅混翼片对流动的明显扰动使横向流动进一步显著增强,中心位置的二次流速度可达3.1 m/s,横向流动的搅混作用产生的涡流促进了不同位置和不同流道之间的热量交换,使温度分布趋于均匀,避免近棒束壁面温度过高,并对定位格架下游出口段的流动和传热产生影响。横向二次流一方面增强了冷却剂与燃料棒束间的热量交换,另一方面也会对燃料棒束结构产生冲击,这种影响将在下述多场耦合模拟中进行分析。
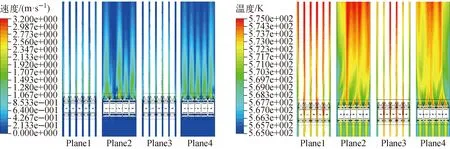
图5 轴向截面冷却剂二次流速度及温度分布云图Fig.5 Contour of secondary flow velocity and temperature distributions at axial-intersection for coolant
图6示出燃料棒束径向各截面(Plane5~8)二次流速度分布云图及局部子通道速度矢量图。由图6可见:由于定位格架内部条带弹簧和刚性突起对冷却剂流动的扰动作用并不强烈,冷却剂在定位格架出口(Plane5,z=33 mm)之前虽出现了横向流动,但并不明显;冷却剂从定位格架流出(Plane6,z=39 mm)后受到搅混翼片的扰动出现强烈的二次流,最大流速达到约3.8 m/s,对应Plane6局部速度矢量图可见形成明显的流动旋涡;随流动继续发展,多个流动旋涡逐渐融合,环绕燃料棒束形成对角线方向更大的绕流(Plane7,z=60 mm),对应Plane7局部速度矢量图可见旋涡的跨棒束分布,直至超过定位格架出口约20倍水力直径(Dh)处绕流的影响才逐步消失(Plane8,z=120 mm)。
2.3 多场耦合条件下冷却剂流动的数值模拟
上述冷却剂流动和传热的数值模拟分析是在固体结构部件完全不变的条件下进行的。实际上由于冷却剂流动产生的冲击和振动,燃料棒束和定位格架会产生相应的形变和移动,特别是定位格架结构中的条带弹簧、刚性突起和搅混翼片形状与位置的改变会反过来对冷却剂的流动特性产生显著影响,进而影响到冷却剂与燃料组件间的传热与温度场的分布。因此需通过多场耦合分析流体与固体间的相互影响。
本文采用ANSYS WORKBENCH软件中的多场求解器MFX进行双向多场耦合分析,建立固体计算域和流体计算域分别使用ANSYS和CFX同时迭代求解。固体计算域内通过功率分布设定将燃料棒束热流量传递给流体域的冷却剂,冷却剂在棒束流道内流动的过程中冷却棒束交换热量,并对燃料组件结构施加力的影响,组件由于流体力和热应力产生形变和位移反过来影响流动和温度的分布。在每个时间步长内通过交错循环的方式实现结构场、温度场、流场三者间的双向数据传递,以此保证每个耦合的时间步都是真实的收敛解,求解流程及多场间的数据传递如图7所示。
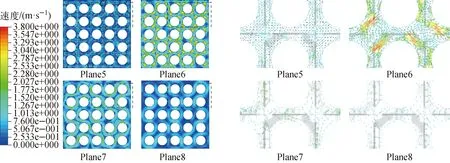
图6 径向截面二次流速度云图及局部速度矢量图Fig.6 Contour of secondary flow velocity and local velocity vector at radial-intersection
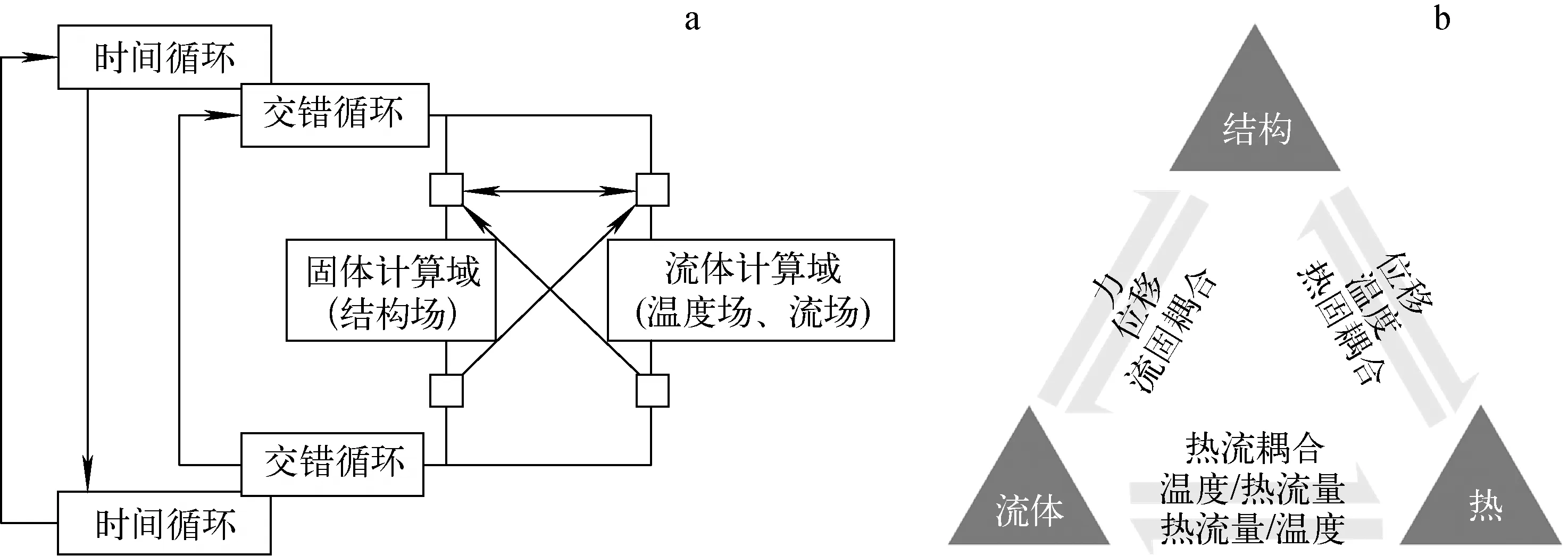
图7 求解流程(a)及数据传递(b)Fig.7 Solving procedure (a) and data transfer (b)
在多场耦合的条件下对冷却剂流动和传热进行数值模拟计算,并与单流场模拟结果进行对比,结果如图8所示。由图8可见,两种条件下二次流速度和温度分布随冷却剂流动的变化趋势是一致的,均是在冷却剂流经定位格架后产生更大的二次流,随流动对格架下游产生影响并逐渐减弱,温度从入口到出口逐渐升高。从二次流速度和温度分布的变化规律来看,两种条件下二次流速度和温度均符合中心通道大于边通道大于角通道的分布规律,考虑到管内流动中壁面对流动的客观影响,这种分布规律符合在相同功率分布的条件下,角通道的流速较低、热量交换效果较差的事实,需注意角通道可能出现局部热点的情况。
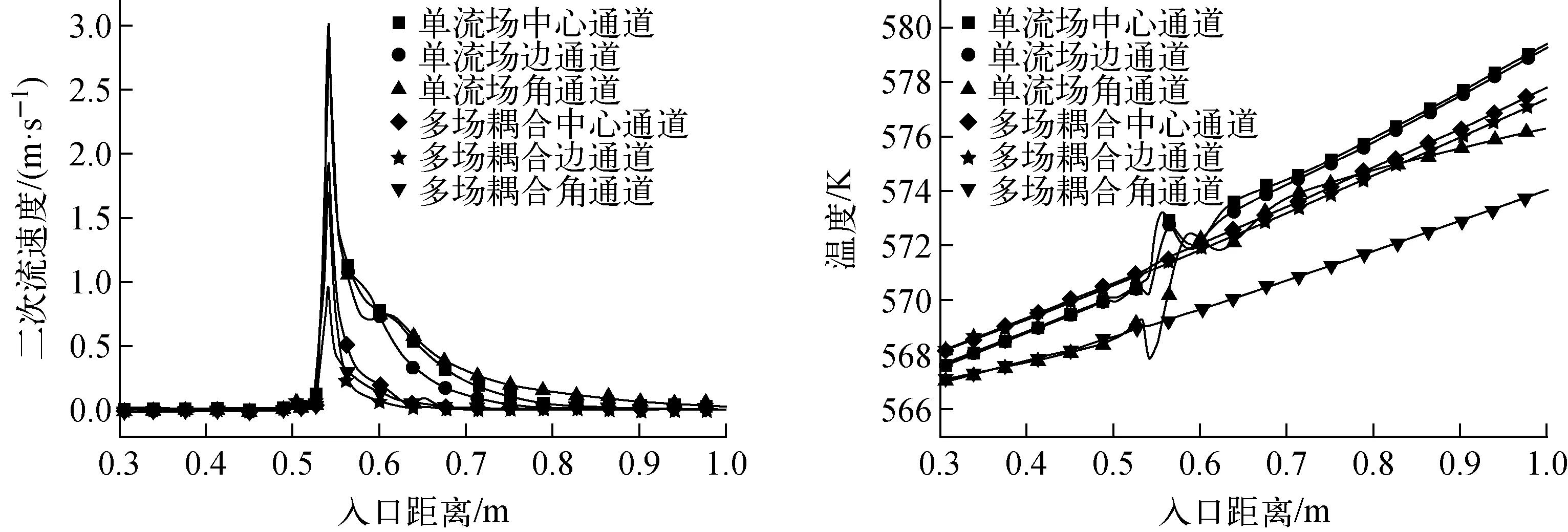
图8 单流场与多场耦合条件下二次流速度与温度的对比Fig.8 Comparison of secondary flow velocity and temperature between single flow field and multi-field coupled cases
另一方面,单流场条件下二次流的峰值速度和平均速度均明显高于多场耦合条件下的分布,冷却剂的温度波动和平均温度均高于多场耦合条件下的分布。这是由于多场耦合时定位格架内结构与冷却剂相互作用使结构形变,特别是搅混翼片受冷却剂冲击产生沿流速方向的变形使冷却剂在流经搅混翼片时受到的阻力降低,较小的流动压降产生较低的横向二次流速度,致使冷却剂与棒束间的换热较弱,冷却剂温度更低。多场耦合条件更贴近于冷却剂流动的实际情况,这一结果对比可避免单流场条件下数值模拟对流动和增强换热过于乐观的估计,可提升安全分析过程的可靠性。以Plane7为例,横向截面的二次流速度分布云图和局部子通道二次流速度矢量图对比(图9)同样可见相同趋势。
2.4 多场耦合条件下燃料棒束的结构特性分析
实际堆芯中冷却剂与燃料棒束是相互作用的:一方面冷却剂受燃料棒束形状结构的影响改变了流场和温度分布,另一方面燃料棒束受到冷却剂传热和流动冲击产生形变和振动改变了结构,是一个双向多场耦合的过程。为分析燃料棒束的结构特性,采用多场耦合条件模拟全长燃料组件7跨中的1跨。考虑到结构和材料特性对棒束两端施加固定约束,定位格架附加弹性约束,格架弹簧基础刚度为2.9 N/mm3 [14]。
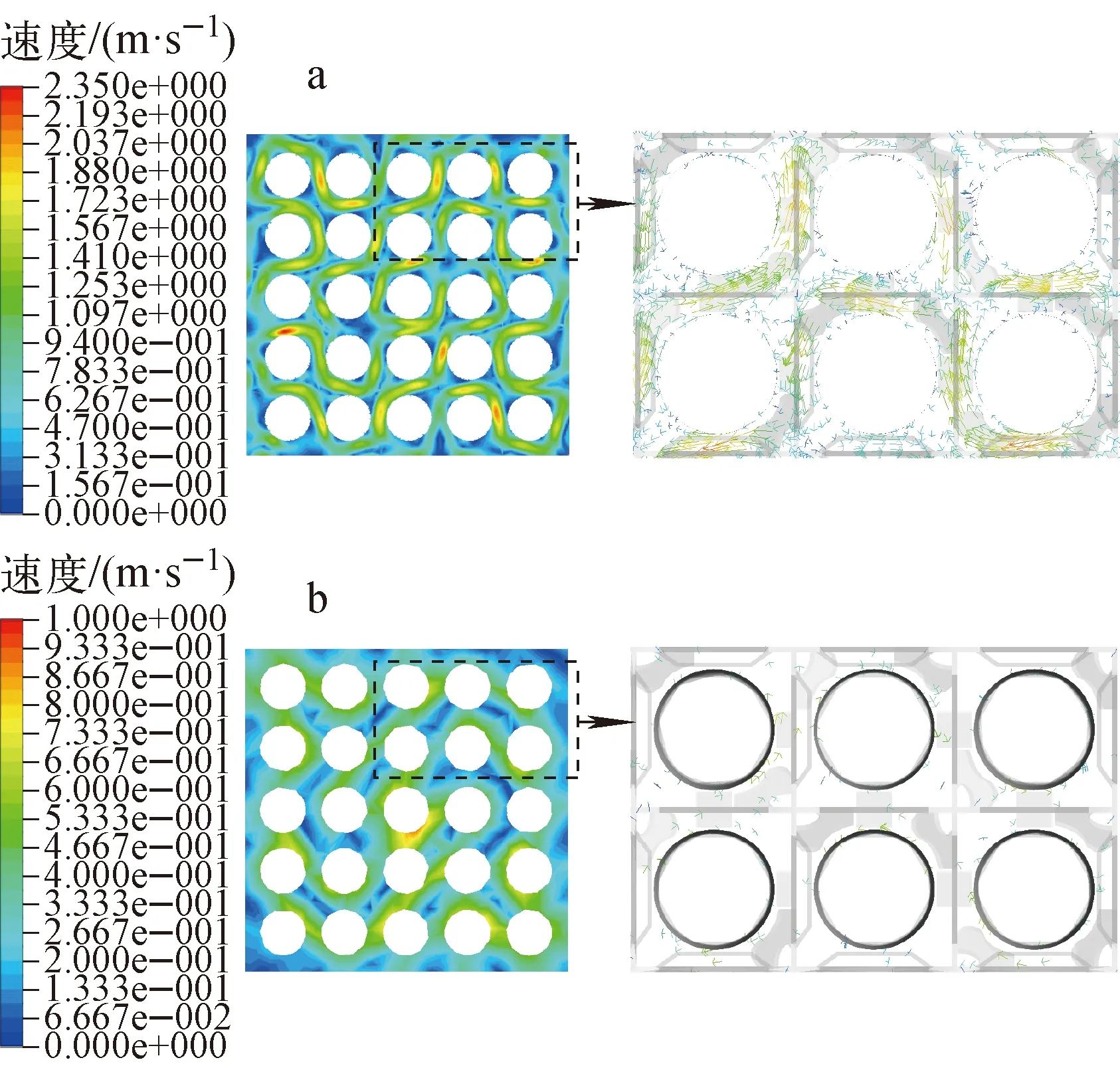
a——单流场条件;b——多场耦合条件图9 Plane7的二次流速度云图及局部速度矢量图对比Fig.9 Comparison of secondary flow velocity contour and local velocity vector of Plane7
从整个燃料棒束结构来看,定位格架搅混翼片自身的功能特性决定了最大形变出现在搅混翼片顶端,最大变形量为2.057 μm(图10)。燃料棒束的形变分布如图11所示。从对安全影响更为关键的燃料棒束来看,最大形变出现在定位格架下游外层棒束的中部,最大变形量为0.653 μm(图11a)。整个棒束结构的形变均为μm量级,形变对结构安全的影响很小。
进一步的模拟中将定位格架从燃料棒束模型中去除,结果显示燃料棒束的形变小于含定位格架的模型,最大形变出现在外侧棒的中部,最大值仅为0.320 μm,燃料棒的形变由中间到两边呈对称分布(图11b)。
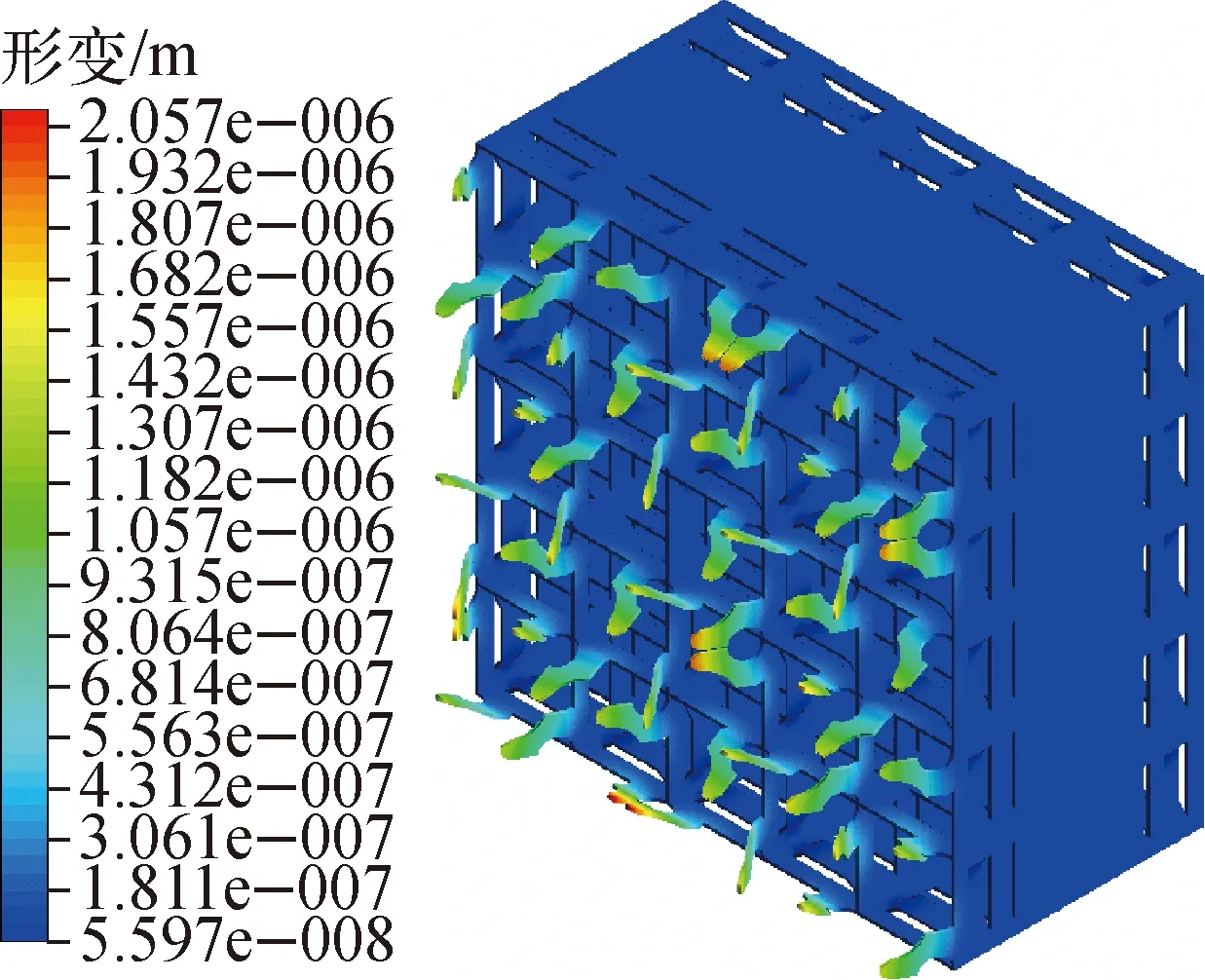
图10 定位格架的形变分布Fig.10 Deformation distribution of grid spacer
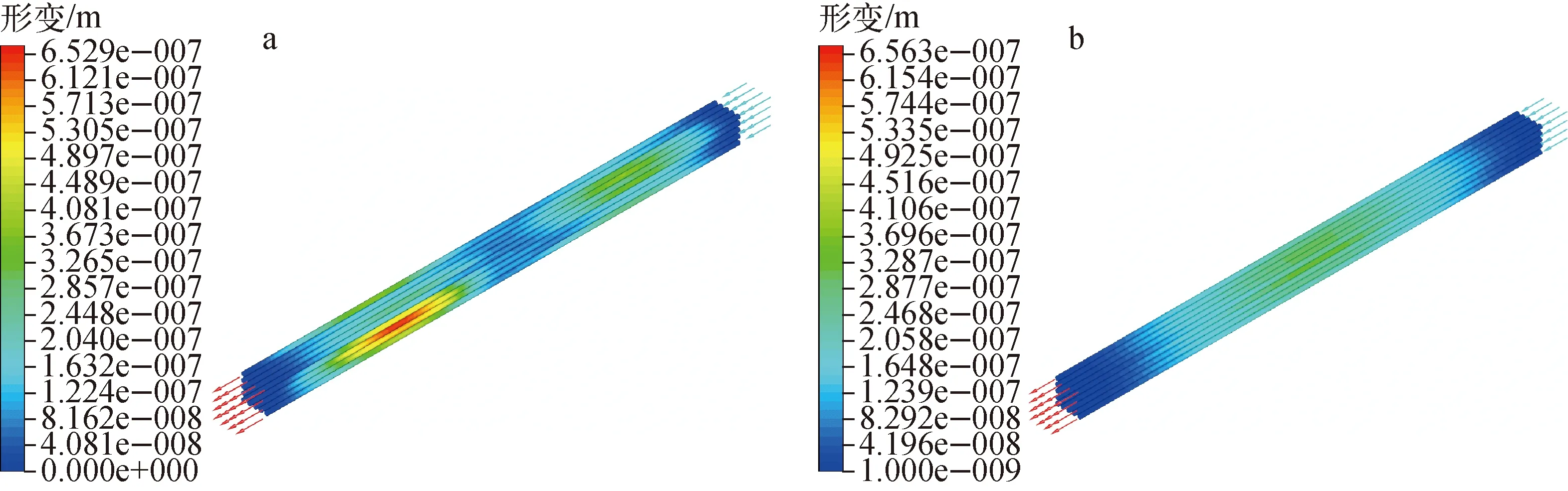
a——隐藏定位格架;b——无定位格架图11 燃料棒束的形变分布Fig.11 Deformation distribution of fuel rod
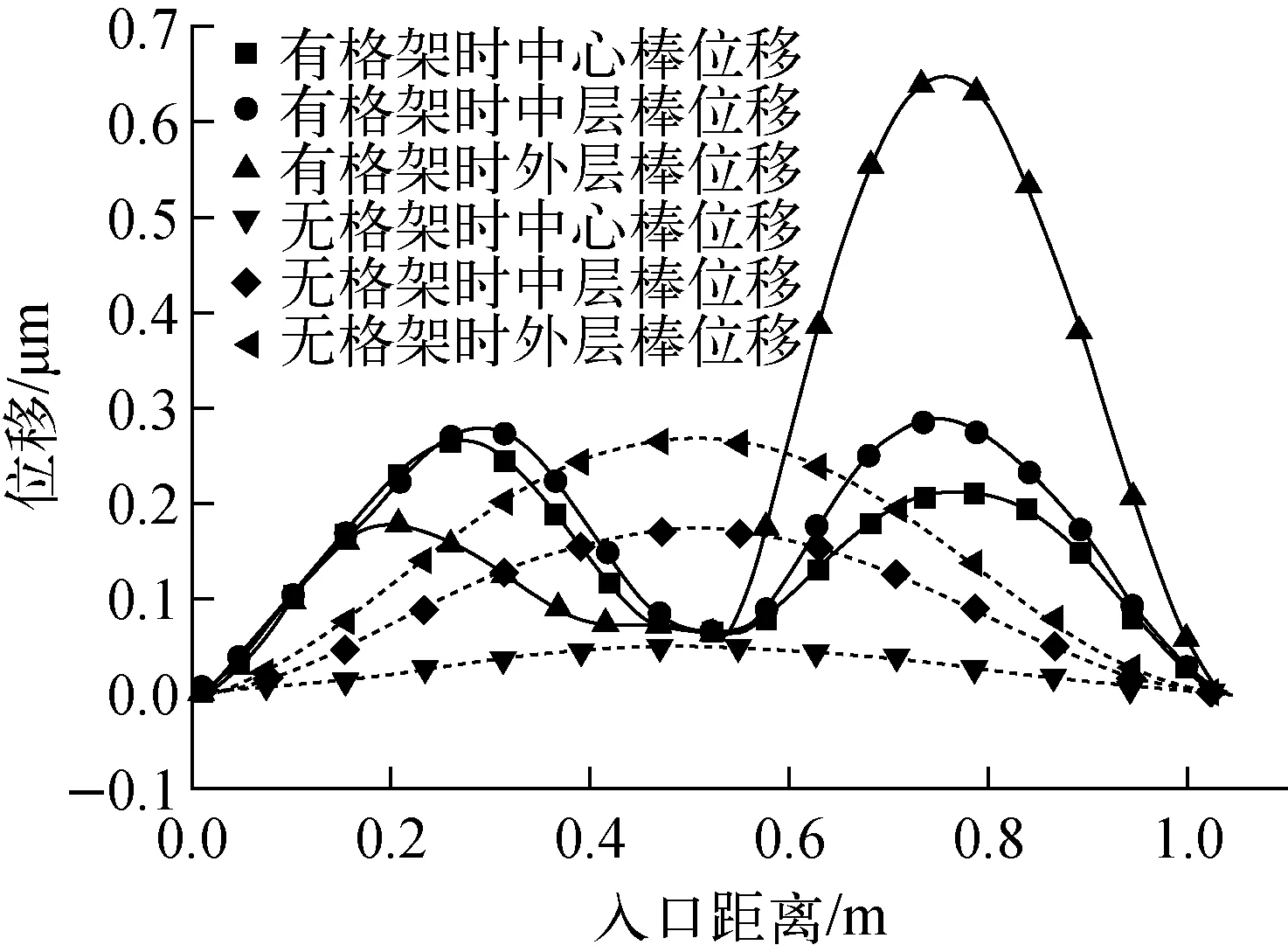
图12 不同位置燃料棒束的形变分布Fig.12 Deformation distribution of fuel rod in different positions
中心棒、中层棒和外层棒沿冷却剂流动方向的形变分布如图12所示。图12中实线所示为有格架情况下的形变,从轴向沿程分布看,由于两端的固定约束和定位格架的弹性约束使燃料棒形变均符合先增长再减小再明显增长最后减小的过程,且定位格架下游棒束形变量明显大于格架上游棒束形变量,这是由于定位格架的搅混作用和燃料棒功率分布特性致使处于不同位置的燃料棒形变分布呈现出不均匀的特点所致。从形变的最大值和平均值来看,外层棒的形变大于中层棒,二者均大于中心棒。结合图9b Plane7的二次流分布可知,形变是由于流动分布不均匀导致的,这种大范围的环绕棒束绕流在棒的两侧分布越不均匀,对棒束横向产生的应力就越大。外层棒由于单侧流动最显著出现了所有棒最大的形变位移,而中心棒附近虽然出现了二次流速度最大值,但两侧流动分布较为均匀,棒的形变是3个位置最小的,中层棒的分布介于两者之间。
图12中虚线所示为无格架情况下的形变,通过对比有无定位格架燃料棒束的形变可知,定位格架对冷却剂流动的搅混作用是明显的,冷却剂的横向流速提升对燃料棒束的冲击增大,使棒束产生更大的径向形变。但冷却剂对棒束的冲击作用有限,燃料棒束最大形变小于1 μm,棒束可保持较好的结构稳定性。
3 结论
本文通过建立冷却剂与含格架燃料棒束的几何模型,采用数值模拟方法获得了冷却剂在5×5含定位格架燃料棒束通道内流动的分布,对比了单流场条件与多场耦合条件下冷却剂的流动和温度分布特性,并开展了冷却剂与燃料棒束间的双向多场耦合分析,得出如下结论。
定位格架通过扰动冷却剂使棒束通道间形成横向流动,并在定位格架下游形成沿对角线流动的绕流,显著增强了冷却剂与燃料棒间的对流换热。多场耦合条件下二次流的峰值速度和平均速度及冷却剂的温度波动和平均温度均小于单流场条件下的分布,前者更贴近于冷却剂流动的实际情况,采用多场耦合条件分析可避免对流动和增强换热过于乐观的估计。在多场耦合条件下冷却剂的横向流动与燃料棒束的热应力使棒束发生轴向和径向的形变,燃料棒束的最大形变量小于1 μm,流动分布不均匀导致燃料棒形变分布呈现出不均匀的特点。有无定位格架的模拟对比表明定位格架的存在使冷却剂的搅混流动明显,冷却剂对燃料棒的冲击也更强,但总地来说两种情况下棒束产生的形变均很小,仍能保持原本结构的稳定。

