一类离散时间非线性多智能体系统的一致性

张星红，何秋锦

一类离散时间非线性多智能体系统的一致性

张星红1，何秋锦2

（1.河南工学院 电气工程与自动化学院，河南 新乡 453003；2.华南农业大学 珠江学院，广东 广州 510900）

研究了离散时间非线性多智能体系统的一致性问题。针对递归非线性模型中的未知参数，利用泰勒展开式推导了投影算法辨识参数。基于把参数估计值作为参数真值的基本设计思想和自适应控制理论中的必然等价原则，利用智能体的邻居历史信息，提出了分布式自适应控制律，使得多智能体系统达到了一致性。最后用仿真验证了理论结果的有效性和可行性。

一致性；多智能体系统；自适应控制；离散时间系统

0 引言

多智能体系统一致性是由多个智能体所组成的系统通过智能体之间的信息交换、协调合作，使得所有智能体的状态趋于一致。其在编队跟踪控制[1,2]、多移动机器人系统[3]、自主水下航行器[4]等实际工程中有着广泛的应用。

多智能体系统的一致性、协同性问题是多智能体系统课题研究的热点之一，并已取得了丰富成果。然而，所得成果大多集中在针对系统内部结构完全已知的连续时间多智能体系统[5-7]。众所周知，在实际系统应用中，通常含有不确定的复杂非线性系统。系统的不确定性也许是系统内部的不确定性，也许是由外界干扰或环境变化等引起的。如何设计适当的控制，使得某一指定的性能指标达到并保持最优或近似最优，正是自适应控制所要解决的问题。因此，研究多智能体系统的自适应控制[8,9]是非常有意义的。

近几十年来，自适应控制技术得到了迅速发展，学者从不同角度对自适应控制进行了分类，如依照时域特性划分，可分成连续时间系统[10]和离散时间系统[11]。在分析控制性能时，连续时间系统的信号和导数是在同一时刻，而离散时间系统的信号和差分是在两个不同时刻。显然研究离散时间的多智能体系统自适应控制较连续时间的难度系数大。近年来，为了在离散时间多智能体系统的自适应控制方面取得理论研究成果，也为了给无人机编队等应用提供理论支撑，很多学者对离散时间含有参数的多智能体系统进行了研究[12-14]。文献[12]研究了一个随机离散时间模型的多智能体系统，智能体之间是以线性形式出现在模型中，在一定的条件下，基于学习和控制的最小二乘算法，所有智能体最终以均方的形式达到了一致。文献[13]研究了一类离散时间线性化参数系统的自适应控制，利用邻居的历史输出信息，设计多智能体系统的分布式自适应控制律。

受以上研究的启发，本文尝试研究一类离散时间非线性化参数多智能体系统的分布式自适应控制问题。利用投影算法辨识系统，基于李雅普诺夫稳定性定理证明了算法的有界性；基于必然等价原则和邻居的历史输出信息，针对每个智能体设计出了既有学习作用又有调节作用的控制律，每个智能体的输出跟踪其邻居前一时刻历史输出信息的均值，在强耦合下所有智能体最终达到了强同步性。

1 预备知识及系统描述

1.1 图论

1.2 系统描述

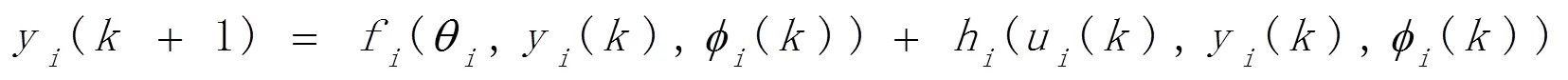
由公式（1）可看出，每个智能体的输出受到其邻居的历史输出信息的影响。

①以电为基础，发展下游产业，延伸电力附加值。目前厅直水电站的上网电价大都在0.2元/kWh左右，在发展多元化产业上，相比而言多少都有一些用电的优势和电价的优势。要加强对产业下游产品的研究，积极延伸产业链，增加电力附加值。

现在给出两个假设条件：

假设1 多智能体系统的邻接矩阵是强连通的。

从假设1可以知道，每个智能体都可以直接或间接地接受来自其他任何一个智能体的历史输出信息，这样每个智能体都不会是孤立的。

本文的目标是讨论含有参数不确定的离散时间非线性多智能体系统的分布式自适应控制问题。首先采用投影算法估计参数值，然后设计出分布式自适应控制律，接着给出多智能体系统的同步性性能，最后通过仿真对理论成果进行验证。

2 投影算法分析

为解决系统内部的不确定性，我们需要先辨识未知参数。基于泰勒展开式的逼近技巧和极值的必要条件定理，采用了投影型参数估计算法来辨识未知参数。首先，采用如下的参数估计准则：

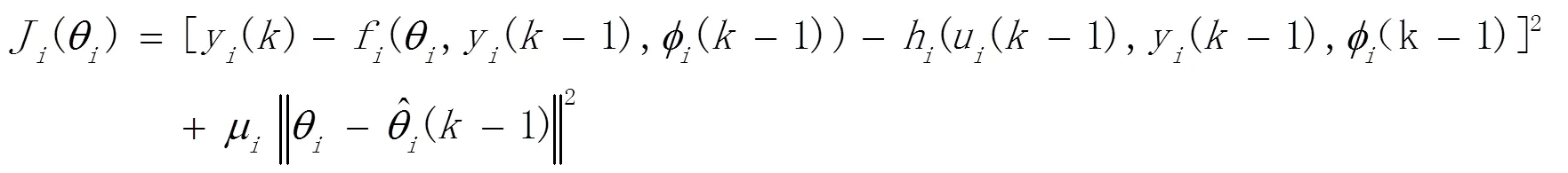
由泰勒展开式，有

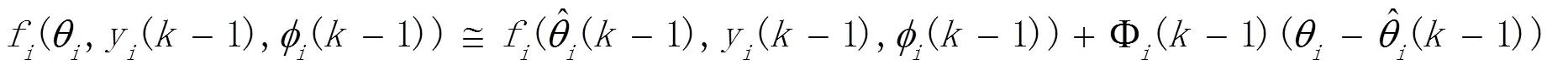
将式（3）和（4）代入式（2），得

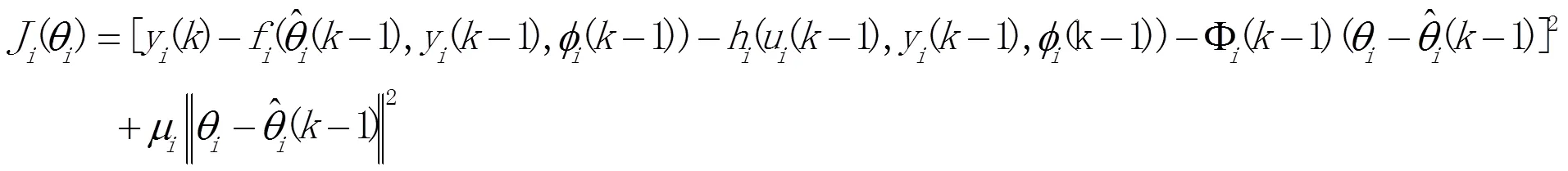
欲使上式取得最小值，依极值的必要条件定理，可推出

整理可得参数更新律

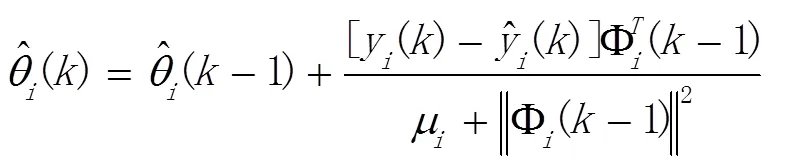
其中，

3 分布式自适应控制器设计

4 系统性能分析

如前所述，参数估计值的更新律和分布式自适应控制律均已获得。本小节主要分析多智能体系统的性能。首先证明每个智能体的输出跟踪其邻居前一时刻历史输出信息的均值，继而证明在强耦合的情形下整个系统达到强同步性。

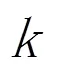
定理2 在假设条件1和2、参数更新律式（6）和分布式自适应控制律式（8）下，多智能体系统达到强同步性，即

5 仿真结果与分析

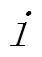
其中，

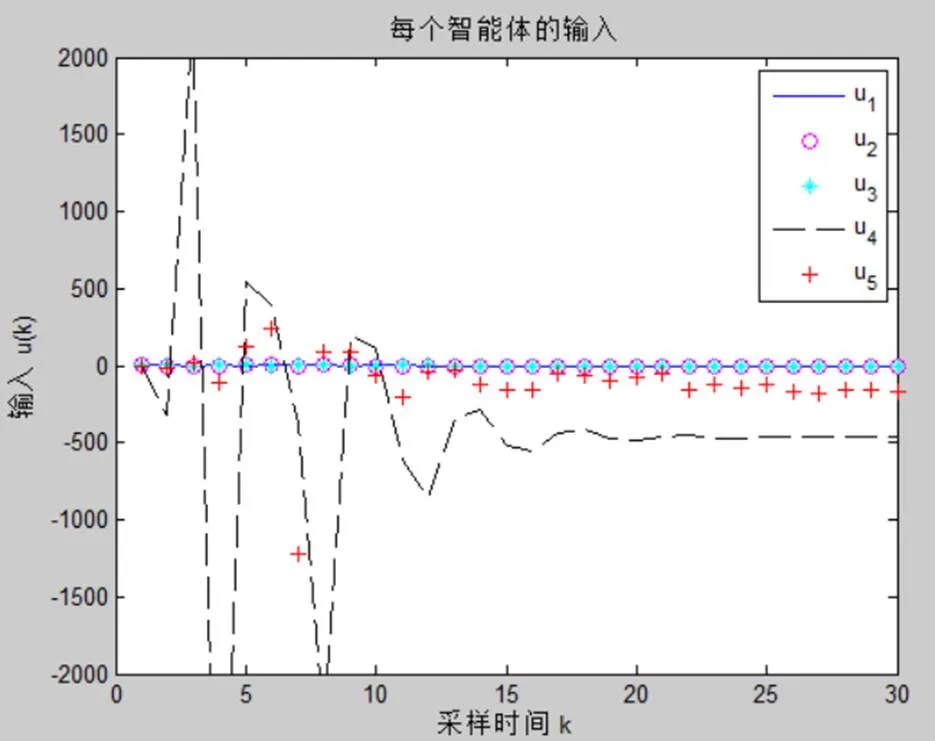
图1 参数估计值跟踪参数真值

图2 每个智能体的输入

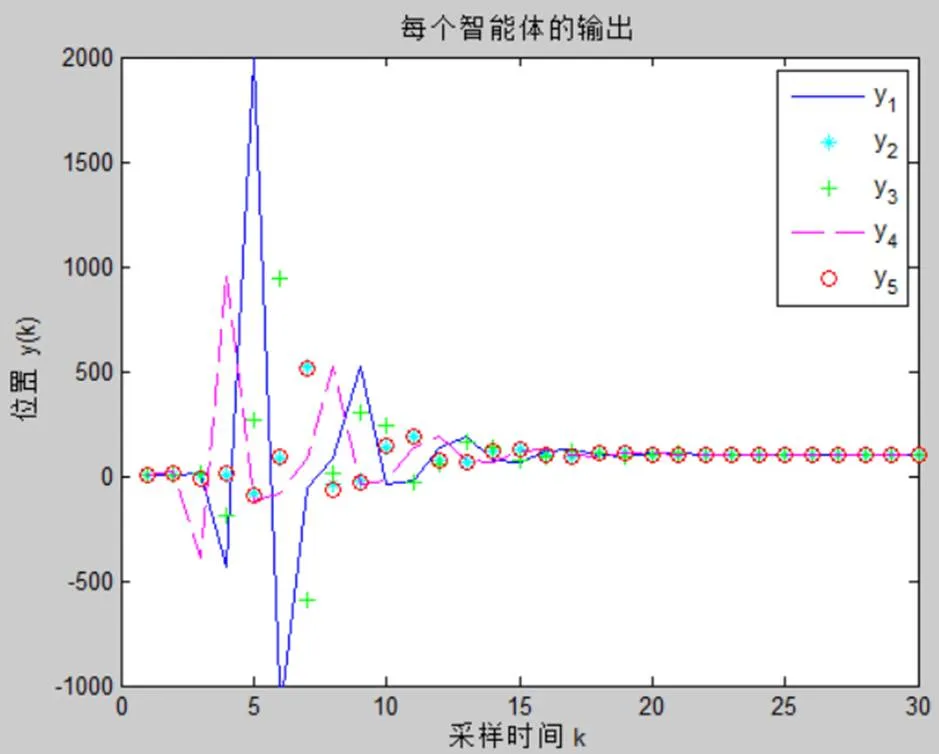
图3 每个智能体的输出

从3个数值仿真图可以看出数值仿真验证了理论结果的正确性。

6 结语

本文研究了一类离散时间非线性多智能体系统一致性问题。在无领导者多智能体系统中，每个智能体仅用了邻居历史输出信息或者参考信号。基于把参数估计值作为参数真值的基本设计思想和自适应控制理论中的必然等价原则设计了耦合分布式自适应控制律，使多智能体系统实现一致性，最后通过数字仿真验证了控制律的有效性。

[1] 冯楚楚.改进的免疫算法在多机器人编队控制中的应用[D].柳州：广西科技大学,2019.

[2] JAVIER A M,EDUARDO M ,TOBIAS N, et al.Distributed multi-robot formation control in dynamic environments[J].Autonomous robots,2018，43：1079-1100.

[3] 姜玉涛,刘忠信,陈增强.带扰动的多非完整移动机器人分布式有限时间一致性控制[J].控制理论与应用,2019,36(5):737-745.

[4] 崔荣鑫,徐德民,许喆, 等.基于Simulink/VRML的自主水下航行器编队控制仿真[J].系统仿真学报,2007,19(13):2881-2884,2894.

[5] HAN L, DONG X W, LI Q D, et al. Formation-containment control for second-order multi-agent systems with time-varying delays[J]. Neurocomputing,2016,218:439-447.

[6] SONG Q, LIU F, SU H S, et al. Semi-global and global containment control of multi-agent systems with second-order dynamics and input saturation[J]. International journal of robust and nonlinear control,2016,26(16):3460-3480.

[7] 冯元珍,刘敏.具有时滞的混合阶多智能体系统的组一致性[J].计算机工程与应用,2019,55(12):67-71,201.

[8] 崔欣.多智能体系统的无模型自适应控制及在多交叉口信号灯协调控制中的应用[D].北京:北京交通大学,2015.

[9] 顾建忠,赵连杰,杨洪勇，等.带有未知参数的多智能体系统的自适分布控制[J].系统科学与数学,2015,35(3):342-353.

[10] 任雪梅.非线性时滞系统的稳定自适应控制[J].智能系统学报,2007,2(5):84-90.

[11] 尹怡欣,孙一康.一种离散时间直接自适应控制算法[J].北京科技大学学报,1999,21(5):502.

[12] MA H B. Decentralized adaptive synchronization of a stochastic discrete-time multi-agent dynamic model[J]. SIAM journal of control and optimization,2009,48(2):859-880.

[13] ZHANG X H, MA H B, YANG C G. Decentralised adaptive control of a class of hidden leader-follower non-linearly parameterised coupled MASs[J].IET control theory and applications,2017,11(17):3016-3025.

The Consensus Problem of a Class of Discrete-time Nonlinear Multi-agent Systems

ZHANG Xing-hong1, HE Qiu-jin2

(1.School of Electrical Engineering and Automation, Henan Institute of Technology, Xinxiang 453003, China; 2.Zhujiang College, South China Agricultural University, Guangzhou 510900, China)

The synchronization problem of discrete-time nonlinear multi-agent systems is considered. First, for the unknown parameter of recursive and nonlinear model, a projection-type parameter estimation algorithm is deduced using the Taylor expansion; based on the basic design idea of the parameter estimation as the parameter true value and the certainty equivalence principle in the adaptive control theory, the distributed adaptive control laws are proposed using the history information of neighborhood agents and the closed-loop system eventually achieves strong synchronization; finally, the simulation verifies the availability and feasibility of the results.

consensus; multi-agent system; adaptive control; discrete-time system

TP273+.2

A

2096–7772(2020)03–0014–05

2020-03-24

2020 年度河南省高等学校重点科研项目（20A20006）；河南工学院高层次人才科研基金项目（KQ1870）；2017 年广东省普通高校特色创新项目（2017GXJK240）

张星红（1980―），女，河南安阳人，讲师，博士，主要从事多智能体系统、自适应控制研究。

（责任编辑吕春红）