岩塞爆破工程水锤压力计算及防护措施

张小莹，张 健， ，陈 胜，贺 蔚

(1.新疆农业大学水利与土木工程学院，新疆 乌鲁木齐 830052； 2.河海大学水利水电学院，江苏 南京 210098)

岩塞爆破是一种水下控制爆破，是在已建成的水库或护坡上修建隧洞进口的一种有效、便捷、经济的施工方法，具有造价低、施工速度快、施工期不受季节影响等特点，近年来在进水口工程中得到越来越多的应用[1]。岩塞爆破的施工工艺特点是将隧洞开挖至库底，临近库底预留一定厚度的岩体(岩塞)，待隧洞建完以后，用爆破的方法一次性爆除预留的岩体，使隧洞与水库贯通。国内外学者对岩塞爆破工程做了很多研究，如李江等[2]通过对刘家峡水电站岩塞爆破模型试验施工技术的研究，总结了岩塞爆破应采用集中药室装药、周边布置欲裂孔的方式；汤帅等[3]运用有限元反应谱的方法分析了水下岩塞爆破对水工建筑物的振动应力的影响，计算得到的结果与实际测量值的分布规律基本一致。

目前有关岩塞爆破工程的研究主要针对岩塞爆破时的药包布置、爆渣处理措施、爆破药量及起爆方式等问题[4-7]，而对上游水库由于爆破产生的压力突增对下游供水管道及相关建筑物的影响及该采取何种水锤防护措施进行安全防护等问题的研究较少。在研究水下岩塞爆破时，不仅需要在施工技术上进行探索，更要对岩塞爆破后产生的巨大水锤压力及其对下游输水系统的影响进行研究[8-11]。黄涛等[12]指出水下岩塞爆破所产生的水中冲击波压力比水中自由场爆炸的冲击波压力要小得多；肖佐庭等[13]通过水工模型试验对密云水库不同水位岩塞爆破后的水力特性进行了研究，得到了典型断面的水流脉动压力特性，给隧洞设计压力的计算提供了依据；李玉柱等[14]采用有压管道非恒定流水体振荡模型处理隧洞岩塞爆破的非恒定流过程，通过对密云和香山水库隧洞岩塞爆破后管道流量及压力的计算验证了模型的可靠性。为了研究岩塞爆破工程在有压管道中产生的巨大水锤压力及对管道系统的影响，本文采用一维特征线法对国内某岩塞爆破工程进行了水力过渡过程的相关计算，并提出了合理的水锤防护措施来保证爆破后管道的安全运行，以期对岩塞爆破工程运行的可靠性进行正确预测提供参考。

1 数学模型及计算方法

岩塞爆破在爆破动力学中主要表现为：爆破产生的爆破冲击波在进水口瞬间产生一个水锤压力峰值，从而在爆破后的数秒至十几秒时间内引起输水系统沿线的压力迅速上升，过大的压力可能会造成供水系统各建筑物的破坏。因此，在进行供水工程的岩塞爆破设计时，需论证岩塞爆破所产生的冲击压力是否会对输水管道及建筑物产生严重危害，是否应采取防护措施来保证整个工程的安全。当岩塞爆破后，水、气、岩渣混合体在爆破压力冲击下于隧洞内迅速形成满流，整个爆破过程所需的时间较短，流态十分复杂，难以进行流态的模拟；此外，满流情况下的水力瞬变过程属于有压瞬变流范畴，因此可采用有压管道中的非恒定流理论进行岩塞爆破的数值模拟分析。特征线法是求解有压管道瞬变流最常用及可靠的一种方法，本文采用一维特征线法进行岩塞爆破工程水力过渡过程仿真计算及水锤防护措施研究。

1.1 有压管道水锤方程

在计算压力管道的非恒定流过渡过程时，基本方程由水流连续方程和动量方程组成，即：

(1)

(2)

式中：Q为管道流量，m3/s；A为管道断面面积，m2；H为测压管水头，m；x为沿管轴线的距离；t为时间，s；a为水锤波波速，m/s；g为重力加速度，m/s2；β为管道纵坡；f为摩阻系数；D为管道直径，m。

采用特征线法，沿特征线将上述水锤的偏微分方程转换为常微分方程，即在t时刻的瞬态水头HP和瞬态流量QP可建立如下特征相容方程：

C+：HP=CP-BPQP

(3)

C-：HP=CM+BMQP

(4)

式中：HP为节点P处的水头，m；QP为节点P处的流量，m3/s；CP、BP、CM、BM为系数，可由前一时刻节点前后的管道参数和水头流量求得。

1.2 岩塞爆破点的控制方程

使用特征线法进行岩塞爆破数值模拟时，岩塞体爆破点模型用阀门模型近似代替，当爆破未开始时对应阀门为关闭状态，发生爆破时，阀门迅速达到全开，设定在很短的时间内，爆破点从静止到起爆对应阀门从关闭到全开的过程。阀门(岩塞体)的过流方程为

(5)

其中ΔHv=Hv1-Hv2

联立式(3)(4)(5)求解可得：

(6)

式中：Qv为爆破节点过流量，m3/s；Cd为流量系数；AG为爆破点处的过流面积，m2；ΔHv为爆破点处的前后测压管水头差，m；Hv1为爆破点首端的测压管水头，m；Hv2为爆破点末端的测压管水头，m；ΔHr为阀门孔口全开时的水头差，m；Qr为阀门全开时的过流量，m3/s；τ为无量纲阀门的流量系数。

1.3 末端闸门井模型

在岩塞爆破工程中，一般情况下将末端闸门井(图1)布置在隧洞的尾端，具有一定的挡水作用，在采用一维特征线法计算时，闸门井的流量连续方程、水头平衡方程、水位流量关系和压力管道相容性方程分别为

图1 末端闸门井数学模型示意图

Qst=Q1

(7)

HP=Zst+RkQst|Qs0|

(8)

Zst=Zst0+0.5Δt(Qst+Qst0)/Ast

(9)

HP=CP-BPQP1

(10)

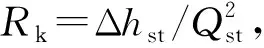
联立式(7)～(10)求解，可得

HP=(CP-C2BP)/(1+C1BP1)

(11)

式中：CP、BP、C1、C2、BP1为时刻t-Δt的已知量，利用式(11)求出HP，即可求出其他瞬变量Zst、QP1、Qst。

1.4 调压井模型

管道系统的调压井数学模型如图2所示，与前述闸门井数学模型建立的步骤相同，在此不再赘述。调压井的流量及水头具体方程如下：

QP1=Qs+QP2

(12)

HP=Zs+RkQs|Qs|

(13)

Zs=Zs0+0.5Δt(Qs+Qs0)/As

(14)

式中：Qs为流入调压井流量，m3/s；As为调压井断面面积，m2；Zs为调压井水位，m；Zs0、Qs0为t-Δt时刻的已知量。

图2 调压井数学模型示意图

2 工程概况及节点布置

某岩塞爆破工程等级为I等，工程规模为大(1)型。工程取水口采用岩塞爆破施工，工程布置如图3所示，主要由进口岩塞爆破段、集渣坑、通风竖井、有压隧洞、1号施工支洞、末端闸门井、封堵体等组成。其中岩塞爆破段长度为12 m，岩塞体为漏斗形；集渣坑位于岩塞体爆破段下侧，长度为44 m；集渣坑下游为通风竖井，直径为1.2 m，通风竖井后为隧洞段，隧洞长度为4 070 m，洞径为7.3 m；隧洞尾部为末端闸门井，闸门井井高81.1 m、长12.78 m、宽11.60 m；封堵体位于闸门井下游，长度为12 m。1号支洞长度为713 m，直径为5.6 m，首部距压力隧洞段首部距离为3 129 m，进口管道底部高程为260.37 m，出口高程为320.00 m。根据技术要求，需要对爆破工程中相关建筑物进行水位、压力、流速、流量及涌浪变化等特性的安全复核计算，以确保工程爆破后输水管道及建筑物能够安全运行。预设爆破时上游水位为316 m。

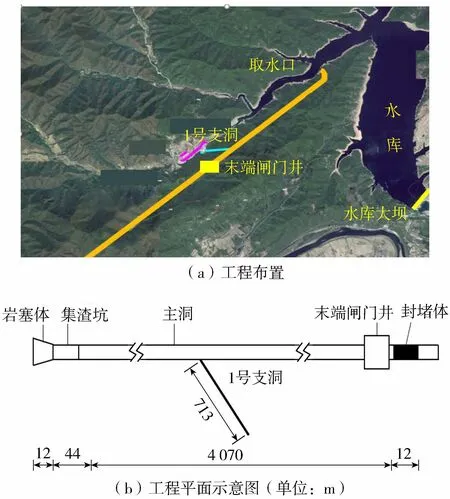
图3 工程布置及平面示意图

由图3(b)可知，整条管道水平长为4 138 m，根据实际布置方式，将整条管路分为62段，共计63个节点(图4)。上游水库为1号节点，距离水库较近的通风竖井为4号节点；1号支洞(30号节点)在数值模拟计算中当量为调压井；末端闸门井为63号节点，利用末端闸门井下游封堵体挡水，将4号、30号节点的溢流水位设为320 m；管道末端闸门井相当于末端管道封堵的溢流式调压井，溢流水位设置为329 m。

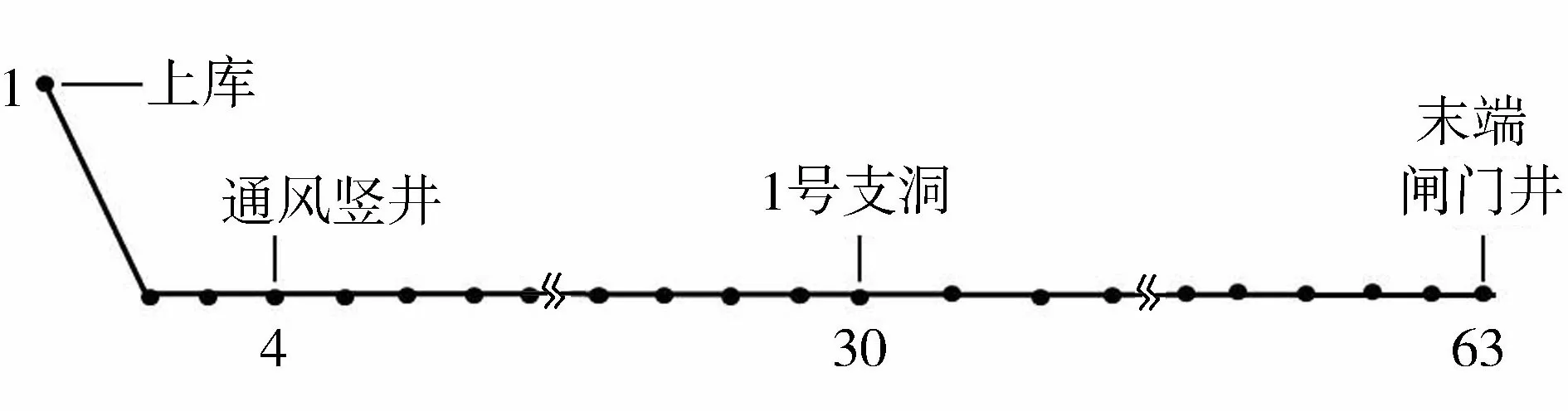
图4 管道节点布置示意图

3 计算结果与分析

在实际爆破过程中，岩塞体爆破瞬间必然释放巨大压力。为了接近实际爆破情况，根据实际爆破工程经验，将岩塞口瞬间爆破产生的压力设为水库静水压力的2.5倍(静水压力51 m(压力均采用压力水柱表示，下同))，当采用特征线法进行水锤压力计算时，上游水库水位随时间的变化如图5所示，爆破开始至0.5 s时间内，上游水库水位由岩塞体高程278 m迅速上升至395 m，持续1 s后又快速降低到水库的稳定水位316 m，当爆破时间超过3 s后，上游水库压力稳定在316 m，恒定不变。

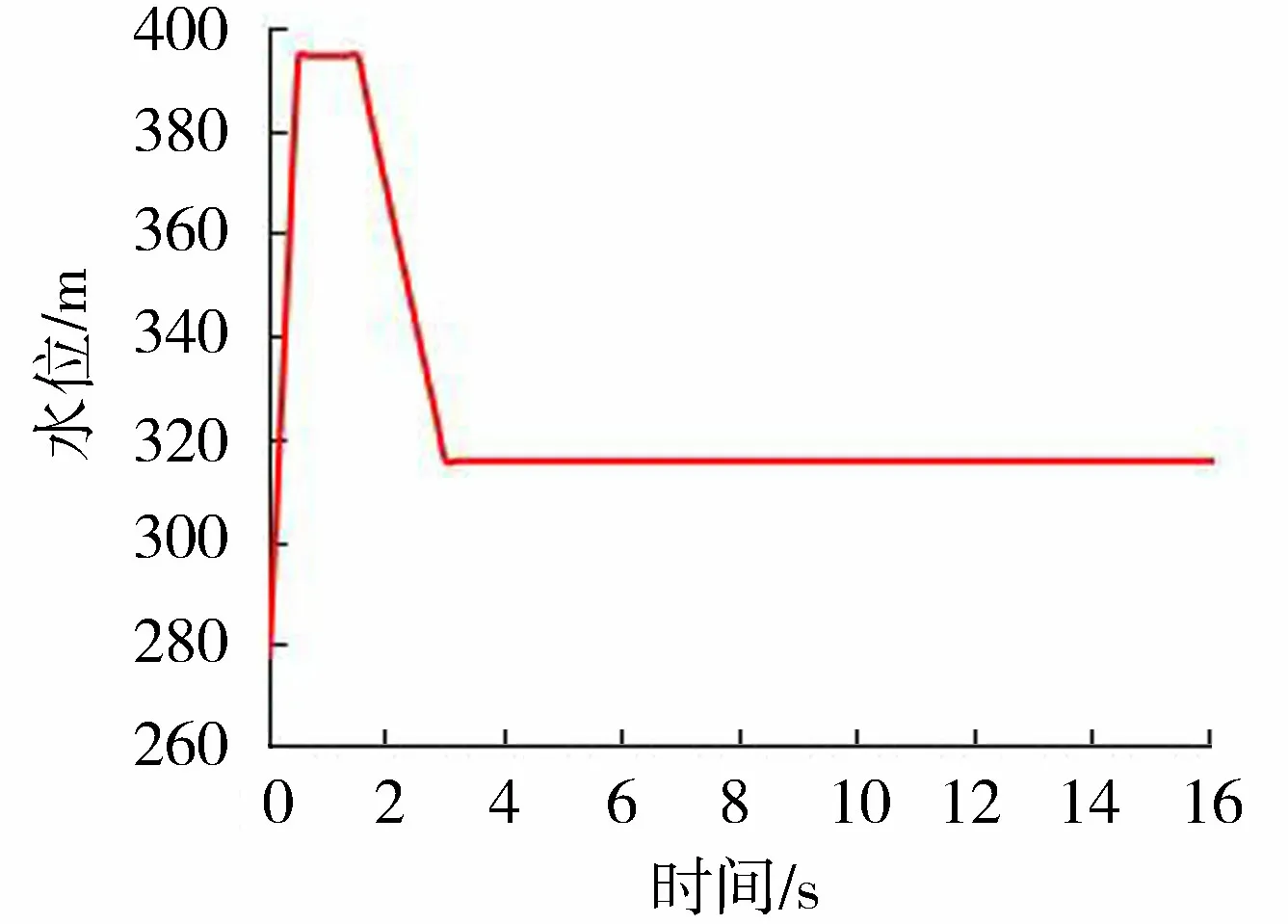
图5 爆破后上游水库水位随时间的变化

管道沿线各个节点水锤压力极值如图6所示，管道中正压极大值为131.64 m，发生在5号节点(通风竖井后100 m位置)，整条管道较大的压力分布在4号节点(通风竖井)至30节点(1号支洞)之间，其压力值均大于131 m，各节点处的压力值相差不大。通风竖井的最大压力为131.59 m，至28号节点处降为126.17 m后又下降至30号节点处的58.00 m。1号支洞后节点压力极值随着节点号的增加逐渐增大，从58.00 m逐渐增大至66.00 m。由图6可知，管线压力最小值为-75.56 m(负压)，发生在19号节点(通风竖井和1号支洞中间位置)。从4号节点(通风竖井)至1号支洞位置，水锤负压极小值大多分布在-75 m左右，1号支洞前管道处负压极为严重，1号支洞后的压力几乎不变化。实际工程中，当压力降至-10 m时，管道中的水体已发生汽化，低于-10 m的压力仅代表负压的严重程度。

图6 不同工况下各节点水锤压力极值分布

由图6可知，整条管道的水锤正压及负压值非常严重，极易发生弥合水锤事故，危及管道的安全。从通风竖井到1号支洞之间的节点水锤正压极值很大，且负压非常严重，受通风竖井和1号支洞两个调压井水位波动和水锤波反射的影响，在这些节点处产生较大水锤压力。由于1号支洞的调压井面积较大，有效地截断了从上游传播过来的压力波，防止压力波再向下游传播，相当于有效缩短了压力管道的距离，所以其后的节点最大水锤压力均较小。虽然通风竖井作为调压井可以减弱水锤压力的传播，但由于通风竖井的面积过小(为1.13 m2)，没有起到很好的水锤防护效果，所以在4～30号节点处的水锤压力过大，当采用此设计方案进行爆破时会对整个管道系统造成破坏。此外，由于闸门井在管道末端，距离上游较远，且1号支洞调压井的面积足够大，管道主要依靠1号支洞消除水锤压力。

由图6可知，处于通风竖井和1号支洞中间位置的19号节点是负压最危险节点，故以该节点作为管道典型节点来分析过渡过程中节点处的水锤压力与流量变化。图7为19号节点的压力及流量随时间的变化关系，可知发生爆破后3.16 s水锤压力值达到最大，为131.26 m，由于水锤波在通风竖井等调压井处发生反射，在5.49 s达到压力最小值，为-75.37 m。水锤压力值呈现周期性变化，虽然1号支洞面积较大，削弱了部分水锤压力，但由于爆破产生的压力巨大，所以19号节点处仍产生了较大水锤压力。流量的变化趋势都是迅速上升后再下降，爆破瞬间，上游水库水位突然升高到395 m，当下游水位不变化时，上下游水位差变大，导致19号节点的过流量突增，所以流量曲线呈现突然上升的趋势；上游水库水位恢复到316 m时，水位差减小，管道流量逐渐减小。

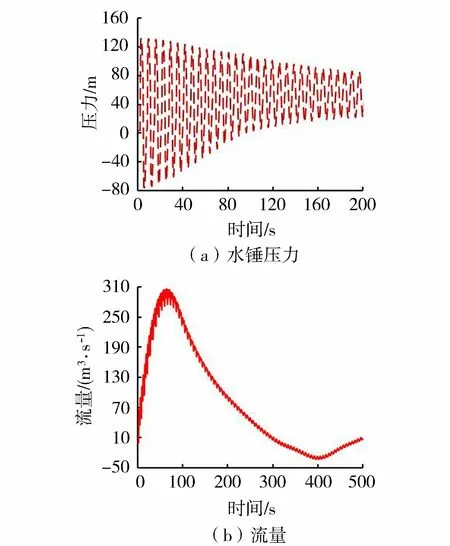
图7 19号节点处水锤压力与流量变化

爆破发生后，若末端闸门井水位超过检修层水位329 m时，检修层将遭到破坏，进而影响闸门井的正常工作，所以计算时亦需考虑闸门井的安全。检修闸门井(63号节点)溢流水位设置为329 m，当该节点水位超过329 m时，检修闸门井会发生溢流。图8为末端闸门井处的水锤压力、水位、流入流量及溢流量随时间的变化，最大压力为第一波压力的极值(65.94 m)，在97.64 s处，随后压力值呈现周期性变化，并呈现逐渐减小的趋势，最终稳定在52 m。水位的变化与压力变化一致，涌浪水位在97.97 s时达到最大329.89 m，第一波最高水位超过溢流水位329 m，闸门井的检修层将被水淹没，随后水位逐渐降低，维持稳定。闸门井流入流量在65.48 s时达到最大，为87.52 m3/s，之后流量流入流出呈现周期变化，当流入闸门井流量较大时，导致管道水位升高，闸门井在94.13 s时发生溢流，溢流时间一直持续23.66 s，在121.63 s后水位开始下降，不再溢流，溢流过程中的最大溢流量为41.62 m3。由上述分析可知，当末端闸门井不挡水时，井内涌浪水位超过检修层最低水位，检修层会被淹没，闸门井发生危险。为了进一步验证数学模型的正确性，进行了物理模型试验，模型按照重力相似准则设计，几何比尺为1∶40.56，岩塞体爆破后，下泄水体压缩隧洞内的水体在末端闸门井处上升，水体上升至闸门井顶部开始溢流，溢流时间持续33.00 s，数值模拟溢流时间持续23.66 s，二者接近，说明本文的数值模拟结果是可信的。

综上，爆破过程中管道的水锤压力超过管道的承压标准，且检修层会被淹没，造成闸门井事故，损失无法预估，所以不建议采用该设计方案直接进行爆破，需要增设水锤防护措施以确保管道的安全。

4 水锤防护措施

为了防止闸门井被淹没，选择将末端闸门井前封堵以避免造成事故。输水系统未增加其他防护措施时主要通过通风竖井和1号支洞这两个调压井消除水锤波，但通风竖井面积很小，水锤防护效果差。岩塞体爆破后上游水库压力变化较大，水位波动较大，需要在输水管道上游处增设水锤防护措施来减小水锤压力。由于通风竖井距离水库较近，在此处设置调压井较为合适，将目前1.2 m的通风竖井面积加大，当竖井面积足够大时即可有效削弱水锤波的传播，使水锤压力有一个释放通道，从而减小输水管道的压力。

为了分析不同面积的通风竖井水锤防护效果，分别将通风竖井直径从1.2 m加大至4.0 m、6.0 m、8.0 m和10.0 m进行水力过渡过程计算，结果如图9所示。由图9可知，当通风竖井直径增大后，通风竖井至1号支洞之间管道沿线压力均明显减小，由于1号支洞面积较大，有效降低了1号支洞后的水锤压力，所以1号支洞后管道压力变化较小。以20号节点为例，当竖井直径从1.2 m增大到4.0 m时，压力变化不大，说明竖井直径增到4.0 m时不能有效消减水锤波；但当直径继续增大到6.0～10.0 m时，压力减小明显，说明竖井面积对管道沿线压力极值的影响较大，通风竖井面积越大，管道压力极值越小，说明加大通风竖井面积的防护措施是可行的。当竖井直径小于或等于8.0 m时，管道中负压值均低于-10.0 m，在汽化压力以下，此时管道内极有可能出现液柱分离现象，危及管道安全；当竖井直径为10.0 m时，负压值在汽化压力之上，满足管道承压要求。

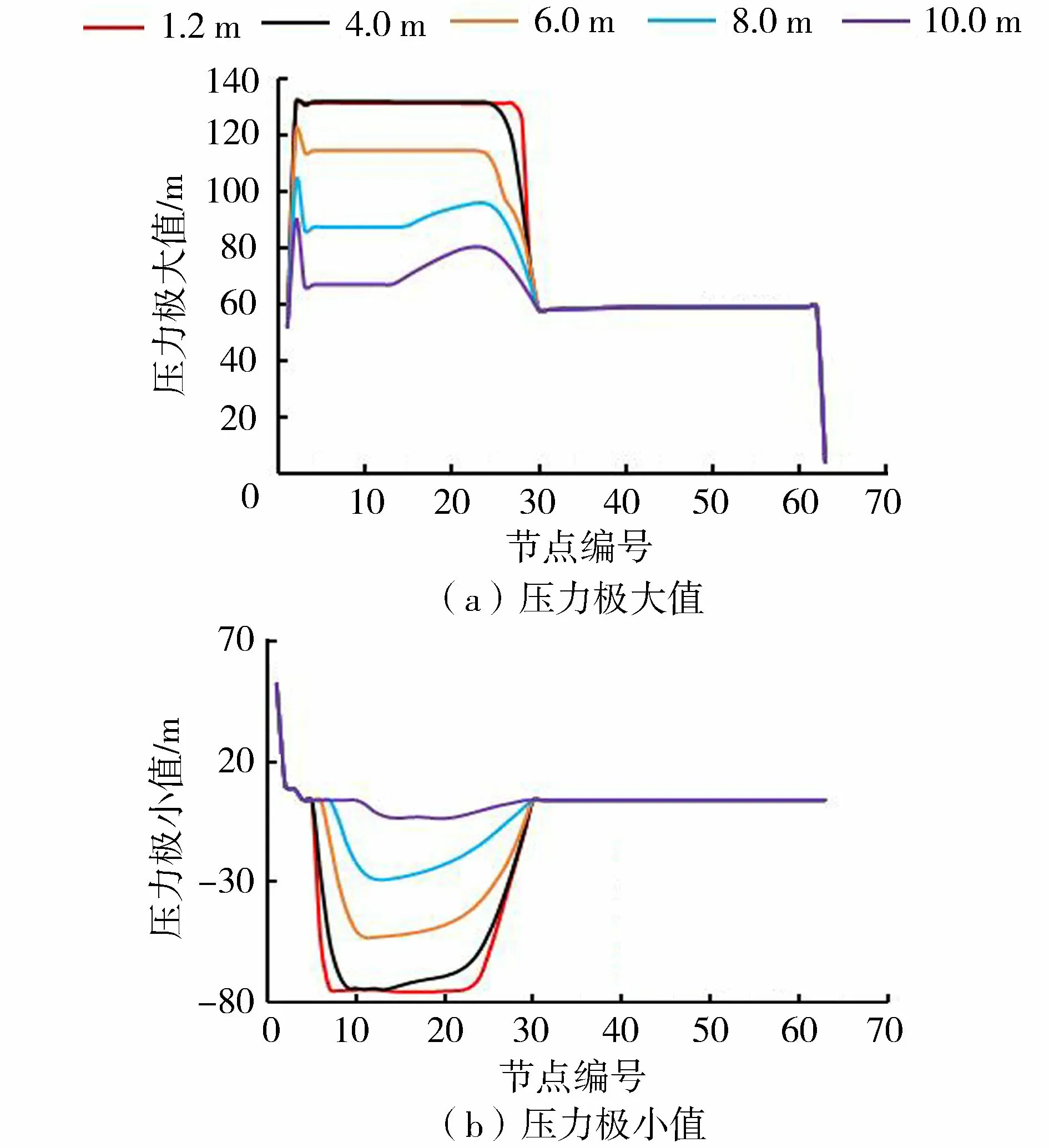
图9 不同通风竖井直径下各节点压力极值变化

图10为不同通风竖井直径下通风竖井处压力极值变化，通风竖井节点处的压力随着直径的增大逐渐减小，最大压力由131.54 m(直径1.2 m)减小到114.61 m(直径6.0 m)再减小到67.02 m(直径10.0 m)。随着通风竖井面积的增大，竖井内压力及涌浪的周期逐渐变长，压力的变化幅值逐渐减小，压力变化越小越有利于沿线水锤压力的防护。图11为不同通风竖井直径下19号节点处压力变化，随着竖井直径增大，19号节点处的压力逐渐减小，压力值由131.26 m(直径1.2 m)减小到114.41 m(直径6.0 m)再减小到76.97 m(直径10.0 m)，负压值由-75.37 m增大到-48.75 m再到-3.71 m。以上计算结果表明，加大通风竖井面积的做法对该爆破工程水锤防护是有利的。随着通风竖井面积的增大，管道的最大压力呈明显的下降趋势，正压及负压都得到了很好的控制，面积越大，压力值越小。当通风竖井直径为10.0 m时，管道负压值均在汽化压力之上，满足管道负压安全控制的最低条件。所以该工程实际爆破前需要加大通风竖井的面积，竖井直径确定为10.0 m时水锤压力满足控制要求，进而保证爆破过程的管道安全运行。

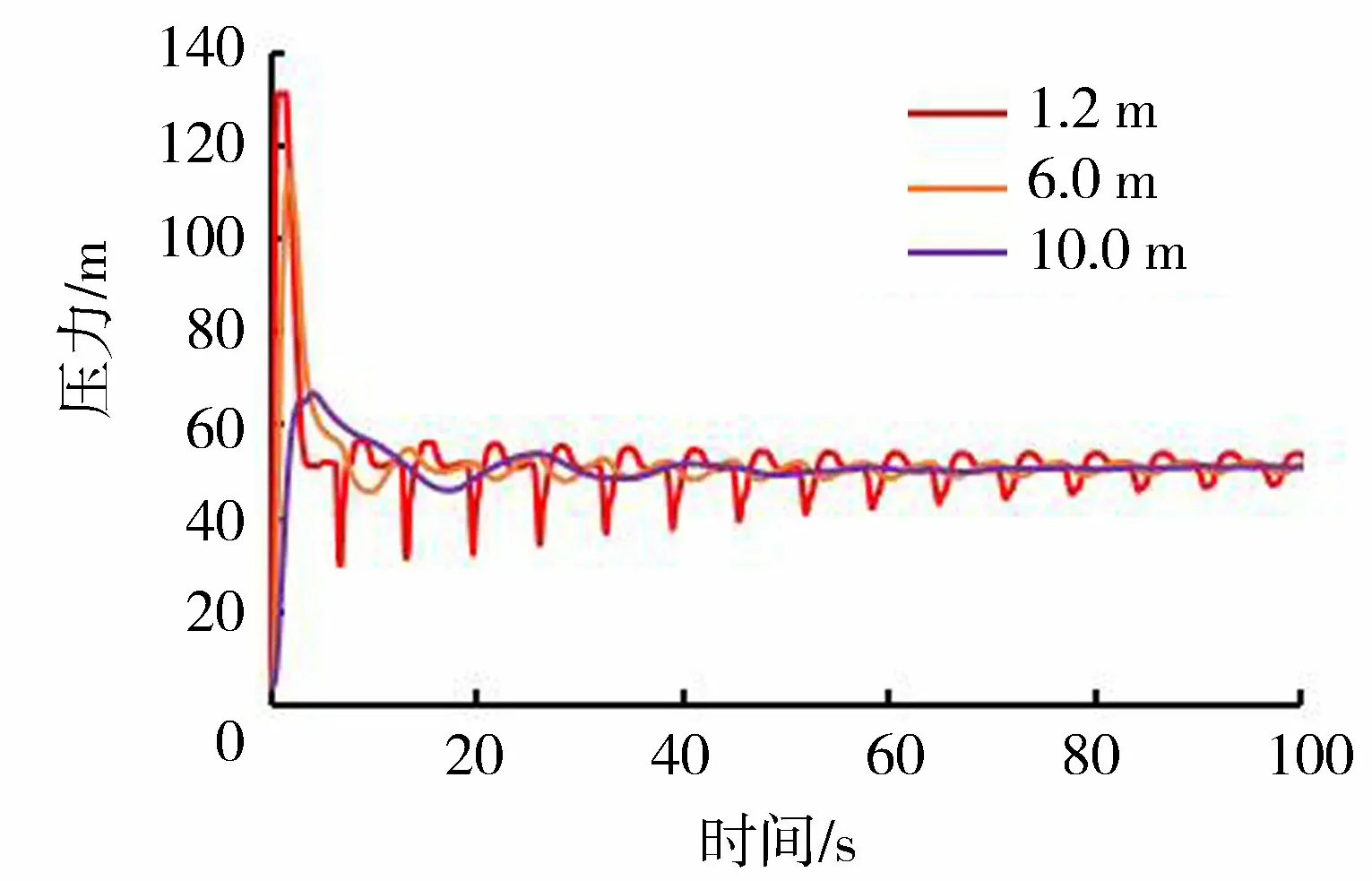
图10 不同通风竖井直径下通风竖井处压力变化

图11 不同通风竖井直径下19号节点处压力变化

5 结 语

本文基于瞬变流基本理论，采用特征线法建立了包含岩塞爆破节点、末端闸门井及调压井等因素的岩塞爆破工程数学模型，模拟了某实际工程上游水库岩塞体爆破后有压管道的水力过渡过程，计算了管道各位置处的水锤压力及流量变化，结果表明：爆破发生后，整条管道的水锤正压及负压非常严重，水锤负压极小，极易发生弥合水锤事故，危及管道的安全，且末端闸门井内涌浪超过检修层最低水位，会发生闸门井事故。由于管道负压严重，需加大通风竖井的面积进行水锤防护，由计算结果可知，竖井面积的加大可以有效地降低管道内的压力极值，正压及负压均得到很好的控制，通风竖井面积越大，管道正压值越小，负压值越大。当竖井直径增大为10.0 m时可满足管道安全控制的最低要求。