具有现实约束的均值-VaR投资组合绩效评价

曾永泉，张 鹏

(1. 仲恺农业工程学院人文与社会科学学院, 广州 510225; 2. 华南师范大学经济与管理学院, 广州 510006)

传统的投资组合绩效评价均采用方差度量风险[1]，如夏普指数、特雷诺指数和詹森指数. 但随着方差的广泛运用，学者们发现方差并不是一个良好的测量风险的方式，方差衡量的是随机变量与期望值之间的上下偏差，而投资者更关心下偏差[2]. 而风险价值(VaR)作为一种下偏差风险度量方法，在风险测量和绩效评价中得到了广泛的应用，如：VaR风险度量方法[3]；在均值-方差模型基础上的均值-VaR模型[4-5]；不允许卖空情况下的均值-方差模型与均值-VaR模型[6]；具有基数约束、上下界限制和交易成本的多阶段均值-VaR模型[7].

在投资组合模型的建构方面，一些学者考虑实际投资市场的诸多摩擦因素，构建了不同的模型并求解. 如：研究了不同借贷利率下以VaR为风险度量方法的投资组合效用最大化模型[8]；在其均值-方差投资组合选择中考虑借款约束[9]. 交易成本同样对投资组合影响颇大，BEST和HLOUSKOVA[10]提出了分段线性交易成本的投资组合模型. 另外，学者们研究了具有基数约束(限制最优资产组合中所含资产的数量)的投资组合模型，使该模型更加符合实际市场上的投资情况. 如：在其均值-方差动态投资组合和市场时机选择中考虑了基数约束这一要素[11]；在研究一系列具有基数约束的投资组合选择问题时提出了一个新的混合整数二次约束的二次规划算法[12]；研究了含区间系数的基数约束投资组合模型，并运用一种新的动态差分进化算法与自适应控制参数求解转换后的确定性模型[13].

实际上，具有基数约束的投资组合模型是一个复杂的非光滑的混合整数规划问题，计算十分复杂，模型真实前沿面的解析解难以得到. 因此，许多学者运用数据包络分析(Data Envelopment Analysis，DEA)法[14]. 如：运用传统的DEA效率评价模型优化投资组合选择[15]；在基金市场上，对30只对冲基金在规模报酬不变的情况下进行了DEA效率估计排名[16]；提出了多元一致性数据包络分析效率分析模型，在传统DEA模型的基础上考虑了投资组合的多样化[17]；将改进的DEA交叉效率模型应用于韩国股票市场投资组合选择，得到了优于传统组合选择方法的结论[18]；构建了多阶段的DEA效率估计模型，在股票市场上对10只风险证券进行了效率估计[19]；比较了前沿面方法和传统评价体系比率在投资决策设计应用中的效果，得到了前沿面评价方法更注重持续性的结论[20]；提出了一种多目标投资组合选择模型，并使用DEA模型进行了交叉效率评价[21].

本文使用BCC-DEA绩效评价方法，对具有交易成本、上下界约束、借款约束和基数约束的均值-VaR模型进行绩效评价，通过上海证券市场的真实数据进行效率估计，构建不同样本数据下的DEA效率估计模型，并构建前沿面与真实前沿面进行对比，分析DEA模型对投资组合绩效评价的有效性.

1 均值-VaR投资组合优化模型

1.1 符号描述和定义说明

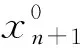
定义1风险(VaR)是指在一定的置信度下，某一投资组合在未来特定时间内最大的可能损失. 设投资组合的期望收益率为rp,则

P(rp<-VaR)≤1-c

(1)

为投资组合的VaR(VaR取正数)，其中，c(1/2≤c≤1)为常数.

定理1[6]当投资组合中n种资产的收益率服从正态分布时，式(1)可转换为

rp≥Φ-1(c)σp-VaR,

(2)

其中，Φ(·)是标准正态分布函数，Φ-1(c)是置信度为c的正态分布函数的下分位点.

随机市场情况下,由式(2)可得VaR风险表达式为Φ-1(c)σp-rTx.

1.2 均值-VaR投资组合模型

假设第i种资产的交易成本函数C(xi)是投资比例的分段线性函数，且为凸函数(图1)，即

(3)

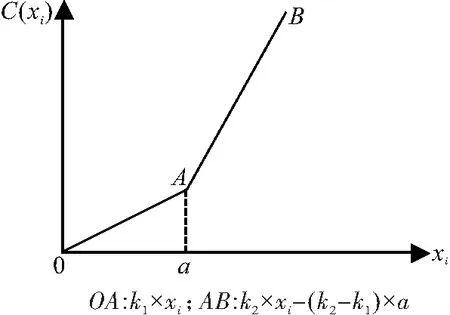
图1 分段线性凸交易成本函数

借款约束是投资组合考虑的另一个重要因素. 本文考虑了无风险资产借款，则投资组合x=(x1,x2,…,xn,xn+1)T的期望收益率可表达为

(4)

其中，

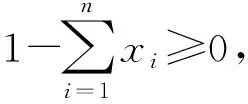
此时投资组合x=(x1,x2,…,xn,xn+1)T的净收益率为

(5)

假设K≥0，且为整数，zi={0,1}，则投资组合x=(x1,x2,…,xn,xn+1)T的基数约束为

lizi≤xi≤uizi(i=1,2,…,n),z1+z2+…+zn≤K.

(6)

投资组合模型的上下限约束为：li≤xi≤ui(i=1,2,…,n).

在文献[22]的基础上，考虑交易成本、上下界约束、借款约束和基数约束等条件，提出以下3个模型.

(1)风险最小化的均值-VaR投资组合模型为：

minΦ-1(c)σp-rTx

(7)

其中，r0表示投资者预期给定收益率. 模型共有4个约束条件：投资组合的净收益率不低于给定的期望值r0、无风险资产有借贷约束、第i种风险资产的投资比例有上下界约束和风险资产投资比例非负个数不能超过K. 模型的经济意义是指在满足上述4个约束条件下，如何使投资组合风险(VaR)最小.

(2)收益最大化的均值-VaR投资组合模型为：

(8)

其中，VaR0表示投资者预期给定的风险. 模型共有4个约束条件：投资组合的风险不高于预期风险VaR0、无风险资产有借贷约束、第i种风险资产的投资比例有上下界约束和风险资产投资比例非负个数不能超过K. 模型的经济意义是指在满足上述4个约束条件下，如何使投资组合收益(r)最大.

(3)效用最大化的均值-VaR投资组合模型为：

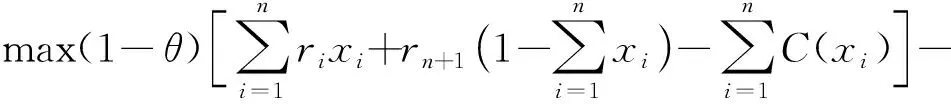
(9)

其中，θ(0≤θ≤1)表示投资者风险偏好系数. 当θ=1时，投资者完全厌恶风险. 当θ=0时，投资者只关心收益，不管风险，此时，模型(9)可以转变为：

(10)

模型(10)属于非光滑的混合整数规划问题，可以运用遗传算法[23]得到其最优解，从而得到该模型目标函数最大值(即r0max)，也可得到VaR0max.

2 均值-VaR投资组合的DEA评价方法

2.1 投资组合效率的定义

为更好地评估投资组合的绩效表现，文献[24]提出了真实前沿面的概念，并基于真实前沿面定义了投资组合效率. 本文根据模型(10)对应的真实前沿面来定义n只风险资产构成的投资组合效率(图2). 图中曲线MNW是n只风险资产构成的投资组合真实前沿面，Q是某一个投资组合.

收益导向的投资组合效率(PEr)是指相同风险下投资组合实际期望收益率与理想期望收益率的比值；风险导向的投资组合效率(PEv)是指相同期望收益率下理想风险与投资组合实际风险的比值. 投资组合Q的收益导向、风险导向的效率可以分别表示为：

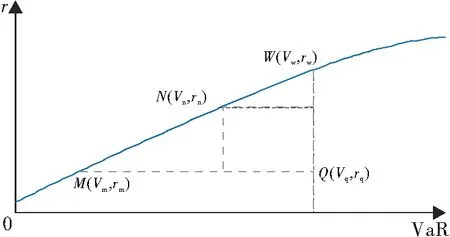
图2 投资组合效率

2.2 均值-VaR的DEA效率评价模型

由于金融市场上的诸多摩擦因素，大规模投资组合难以计算，所以，当投资组合真实前沿面为凹函数时，本文利用DEA模型对决策单元进行投资组合绩效评价.

LIU等[25]运用BCC-DEA模型进行投资组合绩效评价，并指出：若r=h(VaR)是投资组合的前沿面，则r′=h′m(VaR)是m个样本的投资组合的BCC-DEA模型的前沿面，当m→+时，依概率收敛于h(VaR). 另外，若投资组合的风险函数VaR(x)(x为投资组合比例)是凸函数，收益函数r(x)是凹函数且可行域Ω是凸集，则由模型(7)得到的投资组合的真实前沿面是凹函数，可以采用基于数据的BCC-DEA模型对决策单元进行绩效评价. 随着决策单元数量的增加，其前沿面能较好地逼近真实的前沿面.

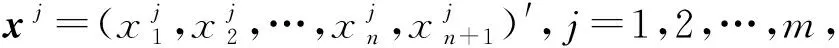
(11)

第j个投资组合的VaR值为

(12)

r0为预先给定的可能性收益率、VaR0为可能性VaR值. 可使用以下3个BCC-DEA评价投资组合的有效性.

(1)风险导向下均值-VaR投资组合的BCC-DEA评价模型：

minθ

(13)

(2)收益导向下均值-VaR投资组合的BCC-DEA评价模型：

maxθ

(14)

(3)效用最大化的均值-VaR投资组合的BCC-DEA评价模型：

(15)

其中，s+代表正偏差，s-代表负偏差.

以上3个模型都是线性规划模型，可以运用线性规划的旋转算法[22]求解.

3 实证研究

本文选择上海A股市场表现较好的30只股票进行分析，股票代码分别为：S1(600000)、S2(600010)、S3(600016)、S4(600029)、S5(600030)、S6(600036)、S7(600048)、S8(600104)、S9(600109)、S10(600111)、S11(600518)、S12(600519)、S13(600637)、S14(600887)、S15(600893)、S16(601166)、S17(601186)、S18(601318)、S19(601336)、S20(601377)、S21(601390)、S22(601601)、S23(601668)、S24(601669)、S25(601688)、S26(601766)、S27(601800)、S28(601818)、S29(601985)、S30(601989). 选择从2010年1月至2019年5月的周收益数据作为样本数据.

鉴于股票市场的高波动性，金融市场上往往通过构造股票投资组合来分散投资风险，而其构成投资组合的股票之间的相关系数越低，分散效果越好. 由30只股票中每一只的股票收益及其与其他29只股票的相关系数(表1)可知：样本中仅3只股票(S5、S21、S25)的相关性系数大于0.5，呈现中度相关性；20只股票的相关性系数介于0.3～0.5之间，具有较弱的相关性；其余7只股票的相关性系数介于0～0.3之间，具有极弱的相关性，可视为不相关. 由此可知，本文所选取的股票样本的总体相关性较弱，可以较好地达到分散风险的效果.

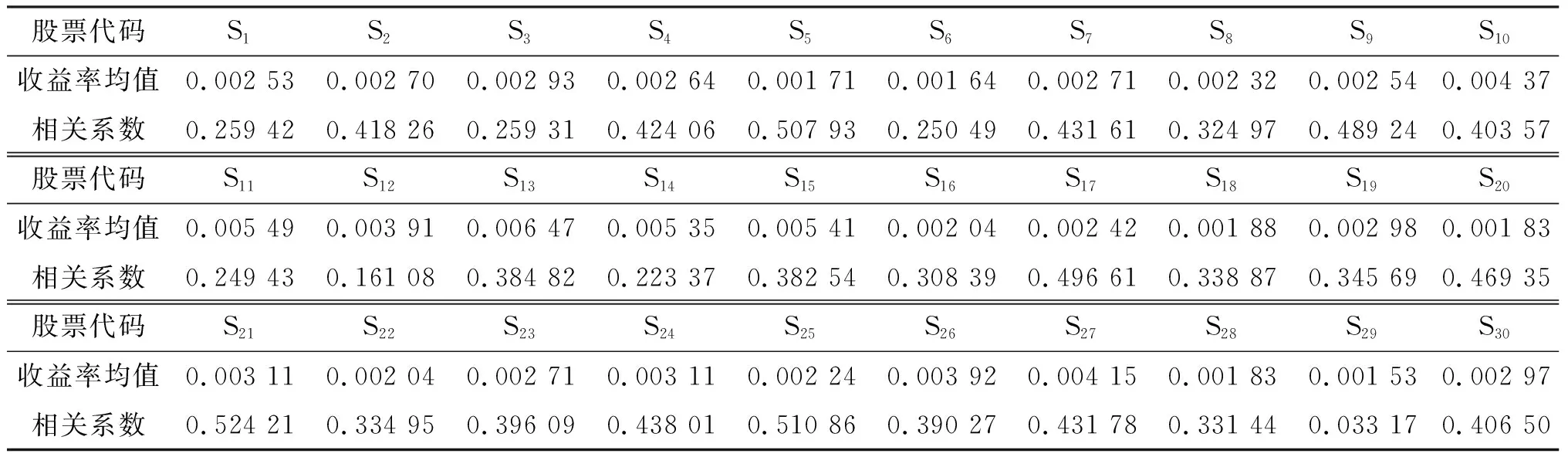
表1 股票收益率均值及其相关性Table 1 The expected return of stock and its correlation

3.1 计算结果

假设分段线性凸交易成本为

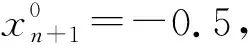
当VaR0在区间[0,0.09]之间变动时，投资组合的真实前沿面如图3所示.

图3 投资组合真实前沿面

当VaR0在区间[0,0.089]之间等距离变动时，净收益率变动情况见表2.

表2 投资组合的净收益率(VaR0[0,0.089])Table 2 The portfolio return when VaR0[0,0.089]

表2 投资组合的净收益率(VaR0[0,0.089])Table 2 The portfolio return when VaR0[0,0.089]

VaR000.0030.0060.0090.0120.0150.0180.0210.0240.0270.030净收益率0.000 400.000 660.000 930.001 190.001 440.001 690.001 940.002 190.002 430.002 670.002 91VaR00.0330.0360.0390.0420.0450.0480.0510.0540.0570.0600.063净收益率0.003 150.003 390.003 630.003 860.004 090.004 320.004 540.004 760.004 980.005 180.005 38VaR00.0660.0690.0720.0750.0780.0810.0840.0870.089净收益率0.005 570.005 750.005 920.006 070.006 210.006 330.006 430.006 510.006 55

由于交易成本、借款约束、上下界约束和基数约束等摩擦因素符合模型(9)的约束条件，所以，本文构造样本数据量m分别为100、200、500、1 000、2 000、4 000的随机投资组合，并将此投资组合的样本数据量代入收益导向的BCC-DEA模型(14)中，从而得到该模型的θ，并根据θ得到有效VaR.

根据表2和表3，可以得到前沿面的对比(图4)，由图可以看出：(1)随着样本数据量m的增大，DEA前沿面逐渐接近于真实前沿面. 根据DEA逼近性原理[25]，当样本数据量足够大时，所得到的前沿面与真实前沿面几近重合，因此，可以近似地把样本数据量足够大的DEA前沿面视为真实前沿面. (2)当风险值小于0.03时，m=200,500,1 000,2 000,4 000的DEA前沿面差距不大，甚至几乎重合，而m=100时前沿面较低；当风险值大于0.07时，m=2 000,4 000的前沿面出现拐点并呈现水平状，而风险值大于0.075时，m=100,200,500,1 000的前沿面也出现拐点并呈现水平状，并不能很有效地接近理论上的真实前沿面.

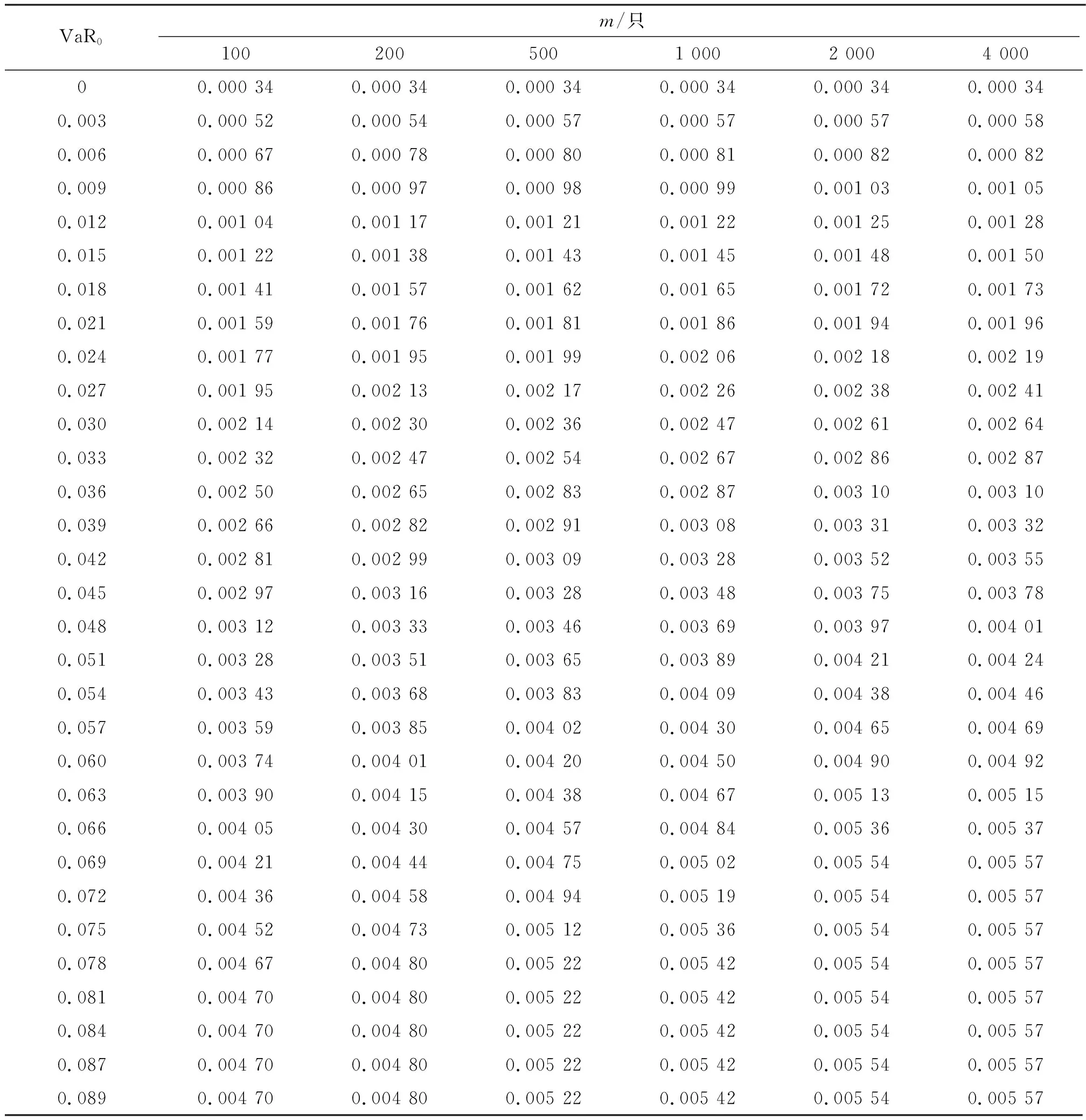
表3 模型(14)的不同风险和样本数据量下的净收益率Table 3 The net return according to different risk and sample sizes in Model(14)

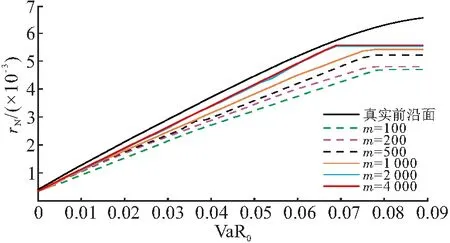
图4 投资组合7种前沿面

3.2 结果分析

针对上述计算结果所得到的结论，从样本数据量出发，对样本收益率均值、不同样本数据量下的净收益率的分布和收敛效果、相关性以及增加样本数据量的代价方面进行讨论.

(1)样本收益率均值的分布分析. 由随机选取的30只股票数据的实际收益率均值分布与正态收益率分布之间的差别(图5)及统计所得到的偏度值(1.101 6)和峰度值(3.352 1)可以看出：至少有18只股票的收益率均值集中分布在[0.001 80,0.003 80]区间内，占比60%以上，这使得在考虑交易成本、借款约束、上下界约束和基数约束等实际约束条件下，后期计算不同样本数据量的净收益时，净收益率会集中在这个区间.

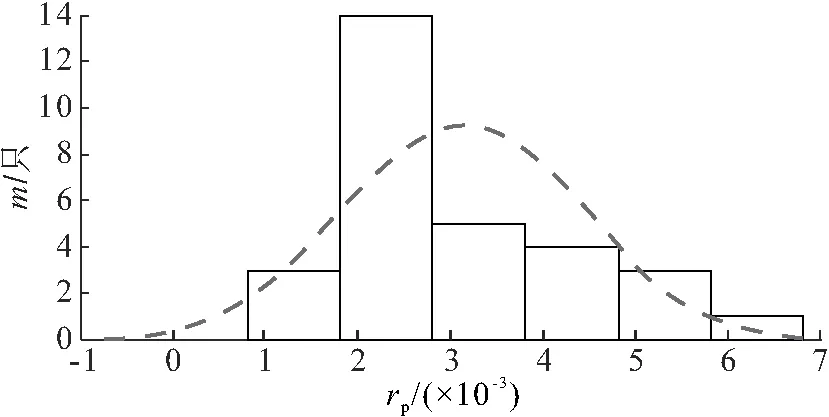
图5 收益率均值分布

(2)DEA前沿面的收敛效果分析. 本文从3个角度验证不同样本数据量下的DEA前沿面的收敛效果.

其一，PEr、PEv和DEA效率值θ间的相关系数与收敛效果. 由真实前沿面得到的收益导向投资组合效率PEr、风险导向投资组合效率PEv与DEA效率值θ间的相关系数(表4)可知：随着样本数据量的增加，PEr、PEv与θ间的相关系数越来越大,两者之间差值越来越小，而由图4可知构造的前沿面越来越逼近真实前沿面，表明m越大，其收敛效果越好.

表4 收益、风险导向效率PEr、PEv与DEA效率值θ间的相关系数Table 4 The correlation coefficents between PEr or PEv and θ

其二，收益率的差值与收敛效果. 由不同风险和不同样本数据量下的净收益率与理想期望收益率的差值(表5)可以看出：在样本数据量相同的情况下，随着风险水平的增加，净收益率与理想期望收益率的差值逐渐增大；在风险水平相同的情况下，随着样本数据量的增加，净收益率与理想期望收益率的差值逐渐缩小，其中，在m=2 000,4 000时，此差值很小，且在2种风险水平下差值相同，可见，DEA前沿面有逐渐接近真实前沿面的趋势.

表5 不同风险和不同样本数据量下的净收益率与理想期望收益率的差值

其三，净收益率区间与收敛效果. 由表3和图4可知：当净收益率rN在区间[0,0.003]区间内取值时，不同样本数据量下的分布区别不大，几乎重合；在[0.004,0.006]区间内取值时，m=200,500,1 000,2 000,4 000的净收益率随着样本数据量的增加而逐渐增加，DEA前沿面逐渐接近真实前沿面；对比m=1 000与m=2 000、4 000的前沿面，随着样本数据量的增加，同一风险水平所对应的净收益值会增多，其对应的风险更为连续，即可以在更低的风险水平下达到最大值，这使得m=2 000、4 000时前沿面出现拐点并呈现水平状.

净收益率rN在m=2 000,4 000时取得最大值，但仅为0.005 57，这与真实前沿面理论下的最大收益率(rN=0.006 55)差距较大，即图4中DEA前沿面的后段与真实前沿面差距较大，并不能很有效地接近理论真实的前沿面.

(3)不同样本数据量运行时间分析. 本文采用Windows7旗舰版系统，CPU型号为Inter(R) Core(TM) i7-870，2.93 Hz. 由程序的运行时间(表6)可知：随着样本数据量的翻倍增加，运行时间呈几何式增加. 在m=2 000,4 000时，相同的风险水平下，其净收益率与理想期望收益率的差值非常小，而运行时间由8 502.8 s增加到35 470.8 s，增长了约4.2倍，这种时间的代价和模拟效果的不匹配，给工作效率带来巨大的困难. 因此，在研究诸如多种限制条件下的前沿面拟合效率问题时，可以基于合理假设适当地修正投资组合对应取值的股票投资比例分布，以减少工作量，提高工作效率.

表6 不同样本数据量下的运行时间Table 6 The operation time for different sizes of sample data s

4 结论

考虑交易成本、借款约束、上下界约束和基数约束等实际约束条件，本文提出了均值-VaR投资组合优化模型. 在投资组合真实前沿面为凹函数的前提下，将BCC-DEA模型作为投资组合的绩效评价方法，根据逼近原理，将DEA前沿面与真实前沿面做对比. 结果显示：(1)尽管投资组合样本数据量不同时得到的前沿面的估计值也不同，但随着样本数据量的增大，DEA前沿面逐渐接近于真实前沿面. (2)当样本数据量足够大时，所得到的前沿面与真实前沿面几近重合，可以近似地把样本数据量足够大的DEA前沿面作为真实前沿面. (3)在逼近过程中，原有的股票样本组合的收益率均值分布呈现出不均匀性，使得不同样本数据量下的DEA模型整体净收益较大值的出现频度进一步减少，整体净收益较小的值差距不大且频度较大，从而导致所得前沿面与真实前沿面差距较大，不能有效地接近真实前沿面.

另外，由收益、风险导向效率PEr、PEv与DEA效率值θ间的相关系数可知：(1)随着样本数据量的增大，两者的相关系数越来越高，证明了本文构造的DEA模型的有效性，样本数据量和逼近效果的关系证明了其收敛性. (2)前沿面拐点较早地出现，DEA前沿面靠近真实前沿面的趋势变慢也进一步证明了收敛效果. 实证研究表明：当样本数据量足够大的时候，构造的样本组合前沿面可以拟合达到理论最优的真实前沿面；随着数据的增加，程序耗时呈几何式的增长，对工作效率影响较大.