循环流化床锅炉高效炉内脱硫理论和关键技术
谭 波,王传志,司 硕,刘忠攀,蓝 天
(1.兖矿集团 洁净煤技术工程研究中心,山东 济宁 273516;2.兖矿科技有限公司,山东 济南 250100)
0 引 言
低成本、无废水、系统简单的炉内脱硫技术是循环流化床锅炉实现洁净燃烧有效和优选途径之一[1-3],由于其廉价易得,石灰石作为脱硫剂广泛应用于循环流化床燃煤锅炉炉内脱硫,其中石灰石的加入量对脱硫效率、灰渣的二次利用[2]有直接影响。关于循环流化床炉内石灰石脱硫已有大量文献报道[4-8],一般认为影响炉内脱硫效率的因素众多,包括石灰石质量、尺寸、床层温度、气氛、氧气含量、加料位置、SO2浓度,Ca/S比等。由于影响因素众多,各研究报道的锅炉、燃料、试验条件不同,数据分散,造成循环流化床炉内脱硫本质的不一致。作为衡量石灰石加入量的主要参数——Ca/S比,在炉内脱硫技术研究中受到广泛关注。邹峥等[9]在一台35 t/h CFB锅炉上进行的炉内脱硫工业试验中发现,Ca/S=2.17时,石灰石在炉内停留100 min后,转化率基本不再发生变化,脱硫效率随Ca/S的增加明显增大,但总体脱硫效率偏低;Ca/S=3.15时,脱硫效率仅为53.5%,这与许多CFB锅炉炉内脱硫研究的理论和试验结果均有较大差距。何宏舟等[10]的工业热态炉内脱硫试验结果显示,脱硫效率随Ca/S的增加而增高,Ca/S大于4.1后,脱硫效率的提高幅度变缓,并趋于一稳定值。其他一些学者的炉内脱硫试验也得出类似结果,即脱硫效率随Ca/S的增加而增大,当大于某一值时,脱硫效率几乎不变[11-13]。对于不同试验设备、试验材料及试验方法,脱硫效率开始趋缓对应的Ca/S值不同,但试验结果均表明,炉内脱硫存在有一个最佳Ca/S比,Ca/S比大于该值时,脱硫效率的增加速率减缓且逐渐趋于稳定[14],甚至下降[15]。脱硫效率与Ca/S比的负指数关系[15]可解释脱硫效率的增加速率减缓现象,但脱硫效率的下降原因还未有合理解释。同时,Ca/S比计算公式中不包含循环流化床大量循环物料[16]中存在的未反应石灰石,因此单纯的Ca/S比不能完全反映石灰石量与脱硫效率的关系。
通过对循环流化床炉内脱硫的深入分析,本文提出“石灰石有效存有量”概念,即将循环流化床锅炉内、外循环中大量未反应的石灰石定义为“石灰石有效存有量”,从新角度论述了决定炉内脱硫效率的本质,由此指出在实际操作中能够提高炉内有效脱硫的关键技术和方法。
1 模型建立
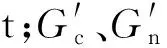
(1)
式中,Gin为石灰石有效存有量,t;Ga为石灰石加入量,t/h;Gf为石灰石随飞灰飞出量,t/h;Gd为石灰石随排渣排出量,t/h;Gs为炉内硫酸钙对应的石灰石量,t/h。
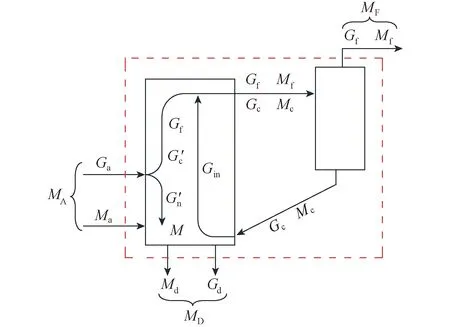
图1 物料循环平衡示意Fig.1 Schematic diagram of the CFB material balance
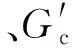
Gin=G1+KG2。
(2)
锅炉采用炉膛底部排渣方式,锅炉排渣量为MD时,则石灰石排出量为
(3)
式(1)可写为
(4)
图2为石灰石有效存有量计算模型,其中,η(SO2)为脱硫效率,%;Bj为入炉燃料燃料量,t/h;Sar、Aar分别为燃料收到基的硫含量和灰分;α1、α2、α3为内循环、外循环、飞灰在灰中的占比;β1、β2、β3为内循环、外循环、随飞灰带出石灰石在灰总量中的占比,则
α1+α2+α3=1,
(5)
β1+β2+β3=1。
(6)
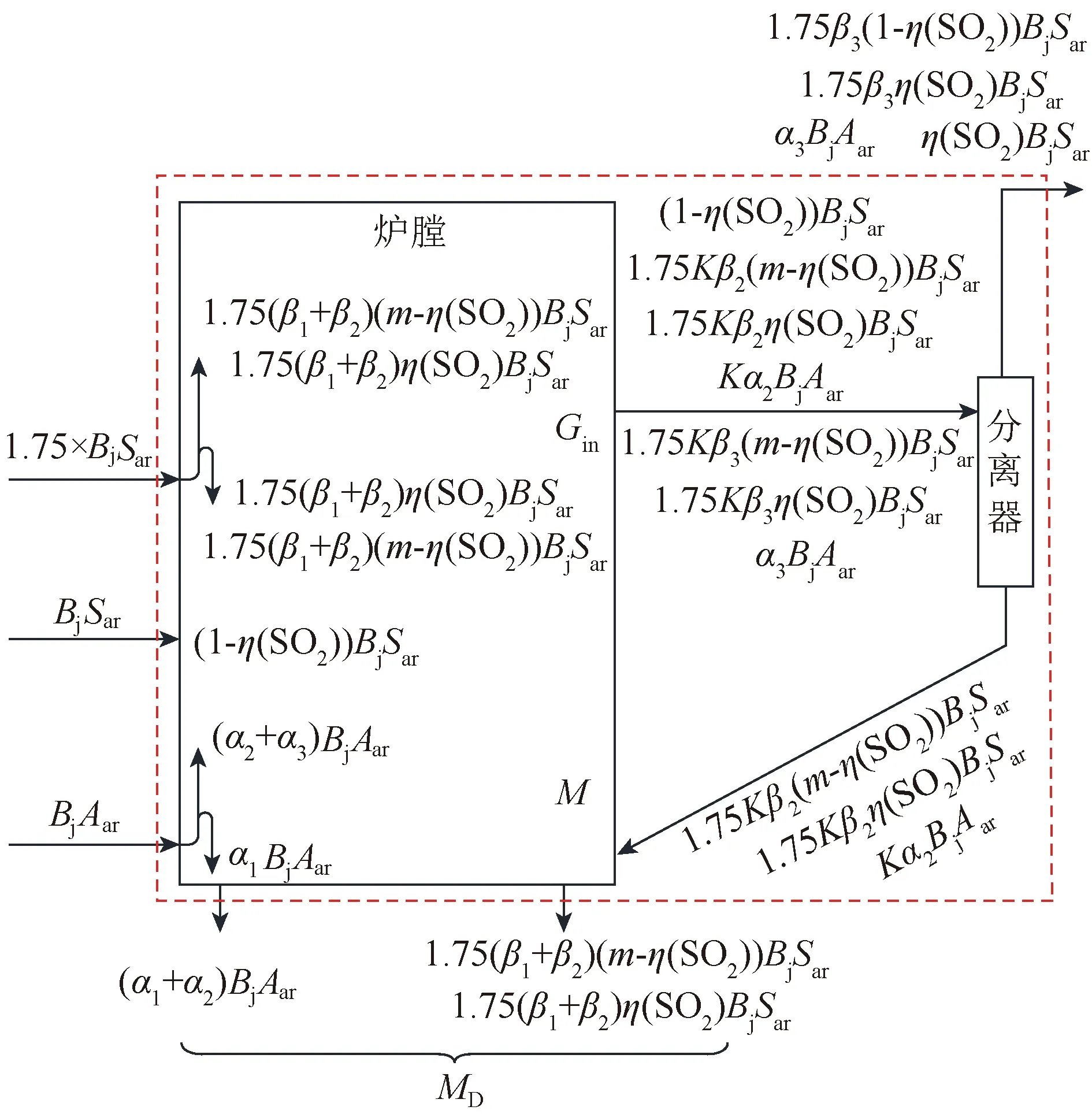
图2 石灰石有效存有量计算模型Fig.2 Computational model of the ″effective limestone inventory mass″
为计算方便,假设入炉石灰石中CaO含量为100%,根据钙硫比m计算公式
(7)
推出石灰石入炉量为
Ga=1.75mBjSar。
(8)
将图2中参数代入式(1)~(4),可得出石灰石有效存有量的计算公式为
(9)
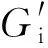
(10)
(11)
由此推出
(12)
当n→∞,可得石灰石有效存有量的计算公式为
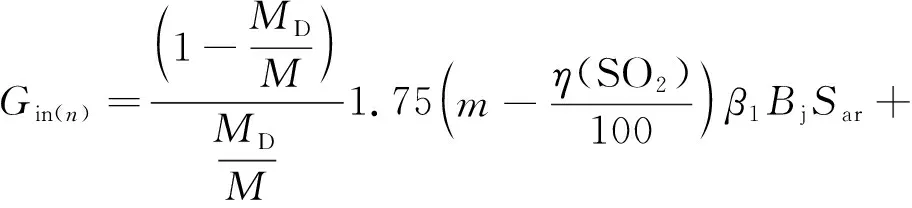
(13)
根据灰平衡关系建立钙硫比m与锅炉排渣量MD间的函数关系MD=g(m),引入修正系数ξ调整,则有
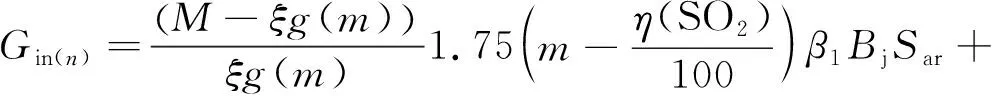
(14)
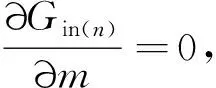
内循环量M由炉膛内存料量与炉膛内床压降的关系[16]计算获得,利用文献[16]中分离器、立管及返料器的灰量计算公式可获得对应的灰量值,3者之和即为外循环量M2,文献[17]给出了循环灰量Mc的计算公式,单位时间内循环次数K为循环灰量Mc与外循环量M2的比值。灰份额(α1、α2、α3)的计算公式来自于文献[17]中相应的飞灰份额计算公式,同时飞灰份额计算公式中含碳量由相应的CaO含量代替,可获得相应石灰石份额(β1、β2、β3)。飞灰、循环灰、底渣的CaO含量与飞灰量Mf、外循环量M2、内循环量M的积为飞灰石灰石量Gf、内循环石灰石量G1、外循环石灰石量G2。由此,可建立石灰石有效存有量计算模型,具体计算公式可参见文献[16-17]。
2 模型计算与分析
2.1 模型计算
利用式(14)对一台75 t/h全煤泥循环流化床锅炉进行脱硫效率计算,并与实际脱硫效率进行比较。石灰石的加入量由Ca/S比表示,其值由式(7)计算,锅炉相关参数为:燃料量18.5 t/h,硫含量0.58%,灰分25.08%。
由式(14)计算得到石灰石有效存有量的最大值为2.52 t,为简化计算,令理想脱硫效率与石灰石存有量成正比,对于理论石灰石有效存有量Gin(theo)和石灰石最大有效存有量Gin(max)有
(15)
式(15)假设所有石灰石在炉内均与SO2气体有效接触,但实际锅炉运行中,由于锅炉入料方式、排渣方式等因素的影响,SO2气体和炉内石灰石可能存在接触不理想的情况,因此引入“气固接触效率”概念,即SO2气体和炉内CaO反应时实际有效接触的石灰石存有量和与理论石灰石存有量的比值,因此,石灰石有效存有量为气固接触效率ηg-s与理论石灰石有效存有量的积。因此式(15)修正为
(16)
由式(16)可预测得到脱硫效率与石灰石入炉量的关系。图3为不同气固接触效率下脱硫效率与钙硫比关系,脱硫效率的计算基础为燃料硫析出量,脱硫效率的计算公式采用式(16)。从图3可以看出,脱硫效率理论计算值和实际脱硫效率值随石灰石加入量的变化趋势相同,并与文献[9-14] 相似,即脱硫效率随石灰石加入量的增加而增大,当大于一定值后,脱硫效率随石灰石的加入量增加而减小。理论计算Ca/S=1.97(石灰石加入量为0.37 t/h)时脱硫效率最大,为100%;实际Ca/S=1.85(石灰石加入量为0.35 t/h)时脱硫效率最大,为86%。Ca/S比在1.5~2.5时的理论脱硫效率在90%以上。
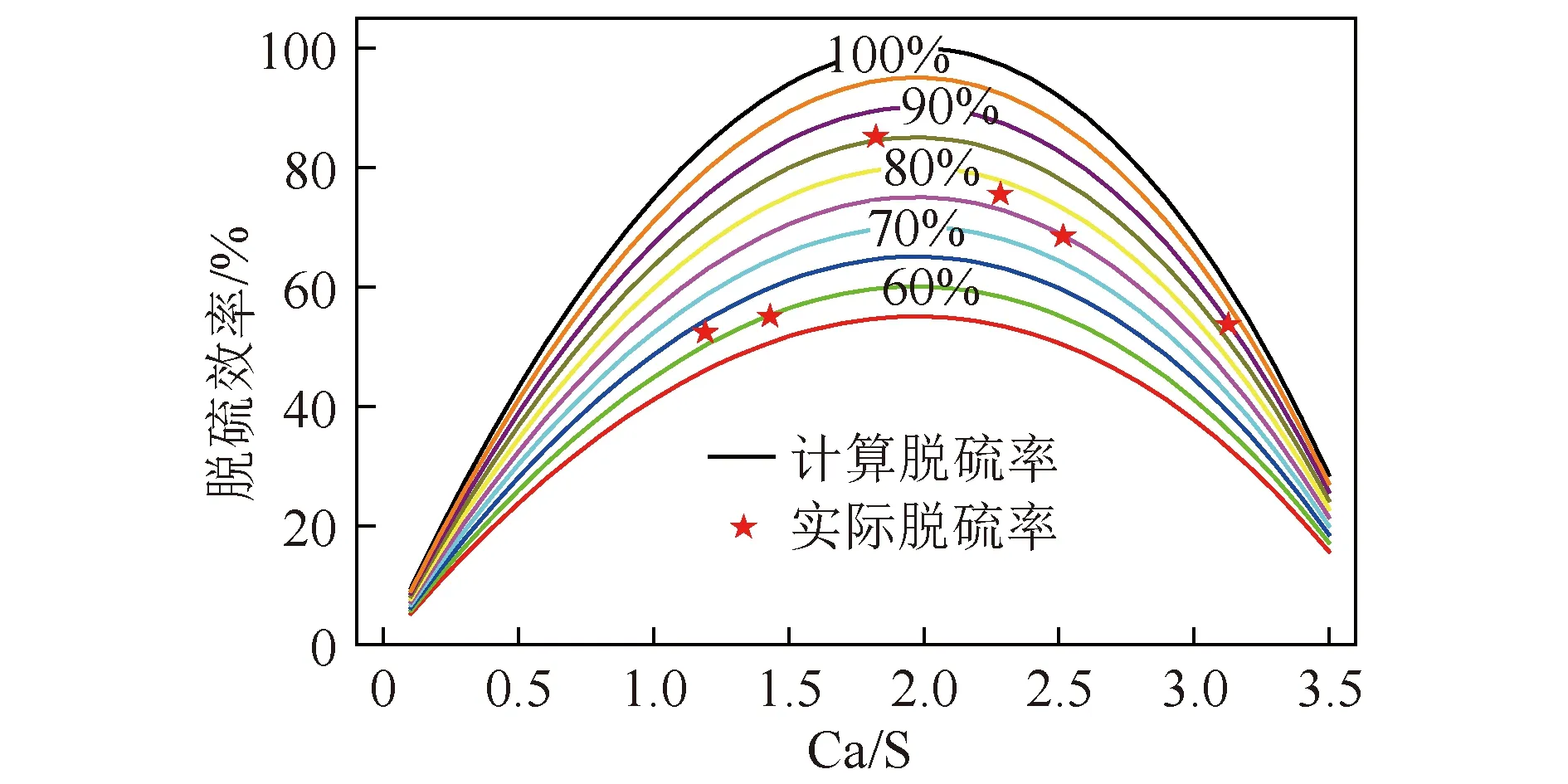
图3 钙硫比与不同气固接触效率的脱硫效率关系Fig.3 Variation of the desulfurization efficiency with the calcium-sulfur ratio for different gas-solid contact efficiencies
由图3可知,由于气固接触效率不同,石灰石加入量相同的条件下,实际脱硫效率不同。对于75 t/h全烧煤泥锅炉,由于其顶部加料方式,煤泥团在从炉膛顶部下落过程中,伴随复杂的加热干燥、热爆破碎、凝聚结团、燃烧等过程,SO2在炉膛上部开始析出,在炉膛出口由于煤粉持续燃烧而不断析出,一定程度上降低了其与炉内循环石灰石的有效接触。因此,相比底部加料方式,SO2气体与石灰石接触效率降低,此时炉内气固接触效率约为85%左右。在低Ca/S(或低石灰石加入量)的情况下,由于炉内石灰石有效存有量小,气固接触机率降低,因而气固接触效率仅60%左右。在高Ca/S(或高石灰石加入量)的情况下,由于排渣量过大,造成炉内有效石灰石存有量降低,气固接触效率为80%~85%。结合预测的气固接触效率,脱硫效率的模型计算和实测值比较如图4所示,可见两者吻合良好,说明脱硫效率与石灰石有效存有量存在良好的相关关系,与石灰石加入量(钙硫比)不直接相关。由此推断,实际决定脱硫效率是“石灰石有效存有量”,而非石灰石加入量(Ca/S比)。
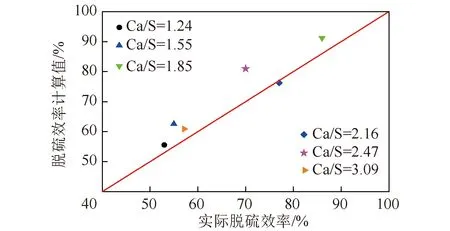
图4 实际脱硫效率与计算脱硫效率对比Fig.4 Comparison of predicted and experimental measured desulfurization efficiencies
对于实际运行的循环流化床锅炉,石灰石有效存有量与循环灰量和循环灰中的CaO含量有关。因此为便于模型,对试验数据进行拟合处理,可得到循环灰中CaO含量X(CaO)与石灰石存有量的关系,并进一步得到试验锅炉脱硫效率与循环灰中CaO含量的关系式,即
η(SO2)=34.28ln(1.315X(CaO)-0.14)+
167e[-0.604(1.315X(CaO)-0.14)]。
(17)
根据式(17)得到脱硫效率与循环灰中CaO含量的关系如图5所示。为进一步验证其有效性,图5同时给出40~440 t/h蒸汽容量循环流化床锅炉实际运行循环灰CaO含量及其对应的脱硫效率(石灰石为同一厂家供应,具有相同品质)。其中,锅炉1为75 t/h全煤泥循环流化床锅炉,锅炉2为440 t/h掺烧煤泥循环流化床锅炉,锅炉3~5为以混煤为燃料的循环流化床锅炉,分别为160、75、40 t/h。由图5可知,计算数据与锅炉2现场测试结果吻合度较高,且锅炉3~5的计算值与现场测试值相近,最大偏差小于3%。对比结果表明,在缺乏确定炉内石灰石有效存有量的情况下,通过分析循环灰样品中的CaO含量,可预测脱硫效率,为判断炉内石灰石脱硫有效性、脱硫石灰石活性、尺寸分布以及操作是否合理等提供简单易行的方法,对现场实际应用具有一定的指导意义。
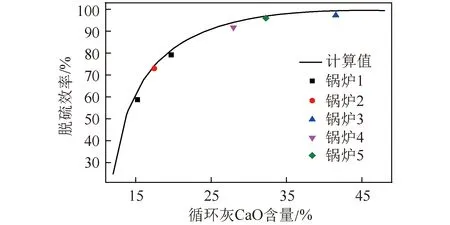
图5 CaO含量与脱硫效率的关系Fig.5 Relationship between CaO content and desulfurization efficiency
上述脱硫效率与循环灰中CaO含量的关系受分离器捕捉能力等因素的影响。因此虽然式(17)对现场实际应用具有一定指导意义,但这些影响因素与本文的研究条件变化较大时,可能需要进一步修正。
2.2 脱硫效率关键技术
由于决定循环流化床炉内脱硫效率的主要因素是“石灰石有效存有量”,则在锅炉实际运行中有效提高炉内“石灰石有效存有量”成为提高炉内脱硫效率的关键。基于建立的模型,对不同粒径分布的石灰石脱硫效率进行分析,计算条件见表1、2,计算结果如图6、7所示。

表1 脱硫效率85%时不同粒径分布的计算条件

表2 内、外循环石灰石量配比
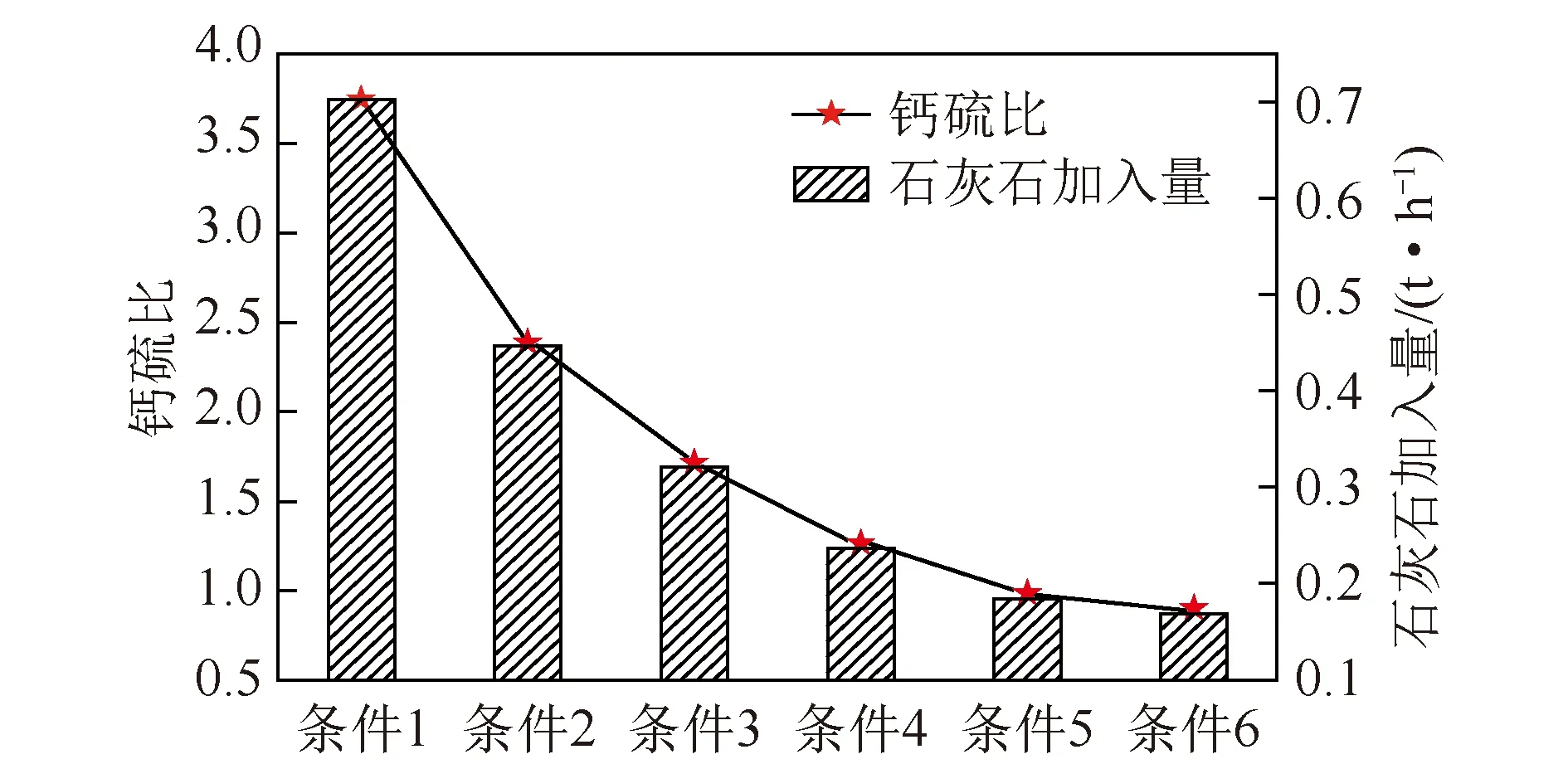
图6 脱硫效率为85%时不同粒度石灰石加入量Fig.6 Adding amount of limestone with different particle size at 85% desulfurization efficiency

图7 不同内、外循环石灰石量条件下的脱硫效率Fig.7 Desulfurization efficiency under different internal and external circulation limestone quantity
从图6可以看出,脱硫效率一定时,石灰石中细粉(即处于飞灰粒径范围内份额)含量越多,需加入的石灰石量越大,主要原因为细粉含量越高,随飞灰带出的石灰石量越大,石灰石有效存有量越小,石灰石加入量越大。细粉含量大于60%时,理论计算值已远偏离工程实际工况,说明此时无法达到85%的脱硫工况。图7为细粉固定份额为30%,参与外循环石灰石量不同条件下的脱硫效率变化。可以看出,随参与循环的石灰石量越多,石灰石有效存有量越大,脱硫效率越高,即在循环倍率一定的条件下,参与外循环的石灰石量越多,脱硫效率越高。
为提高炉内脱硫效率,本文建议采取以下方法:
1)合理选择石灰石粒径,使其最大程度处于循环灰粒径范围内,即在循环时能被分离器捕捉范围内,有效提高石灰石有效存有量,提高脱硫效率。在实际应用时,建议对锅炉飞灰、循环灰、底渣采样并分析其粒度分布,进而调整石灰石粒度分布。在飞灰和循环灰粒度分布交叉很小时(如燃烧颗粒煤时),石灰石粒径分布应与循环灰粒径分布相同或相似;循环灰粒度分布覆盖飞灰粒度时(如燃烧煤泥时),石灰石最小粒径应大于飞灰最大粒径,石灰石最大粒径应小于底渣最小粒径。
2)减少有效石灰石损失。根据dGin/dt=0是石灰石有效存有量达到极值的充要条件,排渣量为石灰石有效存有量的主要影响因素之一,少排、勤排、从炉膛下部排渣是减少有效石灰石量损失的关键。
3)改善气固接触。由于燃煤进料方式、位置的不同以及其他设计或操作因素的影响,炉内SO2释放、流动影响其与循环石灰石的接触, 因此实际锅炉实际运行中需提高SO2与石灰石的接触几率,从而提高石灰石的有效性。
“脱硫效率由石灰石有效存有量决定”的脱硫理论,使根据锅炉运行特性预测炉内脱硫最佳效果成为可能,并由此确定最佳石灰石加入量。石灰石有效存有量在实际操作过程中难以定量测量,但可通过循环灰中的活性CaO含量表征, 脱硫效率和循环灰中的活性CaO含量的关系有待进一步完善。
3 结 论
1)对循环流化床炉内石灰石脱硫进行深入分析,提出了“石灰石有效存有量”的概念,并基于灰循环平衡原理,建立了定量的数学模型。
2)模型计算及实测数据表明,实际决定循环流化床炉内脱硫效率的因素是“石灰石有效存有量”。
3)实现炉内高效脱硫的关键在于:① 优化石灰石粒度分布以有效提高外循环石灰石量和石灰石炉内停留时间;② 合理排渣以减少石灰石有效存有量的损失;③ 提高气-固接触效率以充分利用有效石灰石的活性。

