富水粉细砂围岩隧道地下水渗流特性及支护方案研究

李小丰

富水粉细砂围岩隧道地下水渗流特性及支护方案研究

李小丰

(中铁十八局集团 第五工程有限公司，天津 300459)

玉磨铁路太达村隧道某施工段以粉细砂岩为主，在开挖扰动或遇水时出现涌砂现象，工程性质迅速恶化，对施工进度造成影响。对于富水粉细砂岩隧道中的地下水渗流特性问题，基于地下隧洞围岩稳定性分析中的复变函数法，求得实际马蹄形隧道的形状变换函数和开挖过程中隧道渗流场的数值解。该方法相比于传统圆孔隧道的渗流解析解，具有更高的准确性。结合解析解的预测和实际工程地质条件，分析几种支护、降水方法的合理性。

隧道；渗流特性；粉细砂岩；复变函数；地下水

1 工程概况

新建玉溪至磨憨铁路太达村隧道位于宁洱站~普洱站区间(如图1所示)，进口里程为DK239+810，出口里程为DK245+625，全长5 815 m。隧道最大埋深约180 m。隧区属低中山地貌，洞身分布下第三系渐新至始新统砾岩、砂岩夹泥岩(进口至斜井段约4 000 m)，白垩系下统曼岗组中段泥岩夹砂岩(斜井至出口段约1 800 m)等。洞身发育普洱断裂西支和蛮帕山断层。

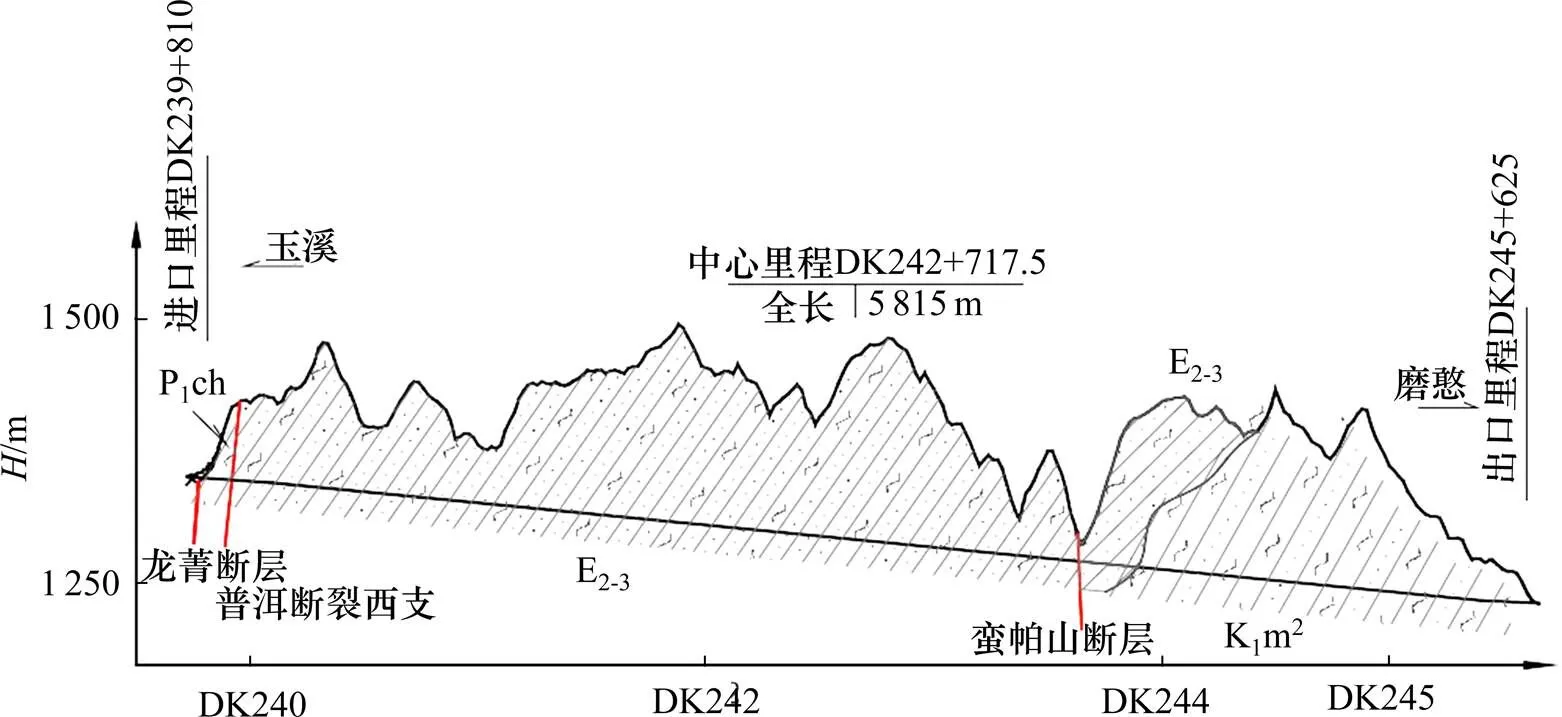
图1 太达村隧道示意图

该隧道DK241+500~DK241+800段属第三系弱胶结砂岩，颗粒组成以细粒为主，颗粒较均一、泥质弱胶结、成岩差，为细粉砂岩。天然状态时，围岩处于密实状，但在遇开挖扰动(现场为非机械开挖)或遇地下水后极易变为散砂、稀糊状(如图2所示)，工程性质迅速恶化，基本失去强度。这种情况下，如果继续开挖，则可能出现涌沙、坍塌等现象[1]。在太达村实际的开挖施工过程中，掌子面的持续涌水涌沙对施工进度造成了极大的影响。

图2 掌子面坍塌

2 围岩条件

为了更好地了解太达村隧道的特殊围岩条件，需要对现场强风化状砂岩进行取样浸泡实验(如图3所示)。据试验观察，取样砂岩经浸泡后，0.5～2 h出现崩解。此外，根据分析，取样砂岩以细粒为主，占71.9%～75.5%，黏粒含量平均约占10.4%；含水程度存在不均，含水率5%～20%；渗透系数5×10−5～2×10−4cm/s，孔隙率26%～31%。

经取水样复核地下水侵蚀性，与勘察资料吻合，该段地下水无侵蚀性。

(a) 浸水前(上)；(b) 浸水后

3 地下水渗流场分析

太达村隧道富水细粉砂岩的工程特性较为特殊，在其他工程案例中较为少见。在隧道开挖的过程中，由于受到扰动，围岩会变得更加松散，甚至会形成空腔区域，同时周围的地下水不断渗入，围岩逐渐软化，使得围岩达到饱和状态[1]最终导致涌沙、坍塌现象。

因此，为了能够充分了解实际工程中富水细粉砂岩地区的隧道地下水渗流特性，以便更好地指导围岩防水和支护，需要运用理论分析对隧道的地下水渗流特性进行预测和模拟。

3.1 地下水渗流特性解析解

在大多数的浅埋隧道分析中，隧道围岩常被假设为半无限空间。近年来，许多中外学者[2−7]对半无限空间下的隧道渗流问题推导了解析解，但是，部分理论解由于计算过程繁琐，边界条件限制复杂，只能简单将隧道断面假设为圆形，与实际工程中的形状差别较大；在这种情况下，复变函数法常被用于求解半无限空间下的隧道断面的渗流问题[8−11]，因为此条件下较容易求得隧道准确的映射函数，从而可以各种形状断面的隧道断面映射为像平面上的矩形区域，从而大大简化问题。但是，当隧道断面不规则时，已有文献[2−7]的方法求解的精度往往较低，不能达到所需的要求。

因此，为了能够提高计算精度，需要通过保角变换引入新的映射函数，将物理平面上形状比较复杂的隧道断面，变换到像平面上边界形状简单的区域，然后在变换后的区域上求解拉普拉斯方程，这种方法不仅可以适应于各种形状的复杂断面(如马蹄形)，同时也可以保证计算效率和精度。

3.2 基本假设

本文选取太达村隧道DK241+650附近的断面，根据实际工程地质条件，在预设的计算模型中，可以做出以下几点假定：

1) 将马蹄形隧道的周围岩土体假设成一个带孔的半无限空间，且为各向同性材料；

2) 地下水补给充沛，且为等水头，不可压缩，隧道内的排水工程对于地下水位的短期影响暂不考虑；

3) 隧道断面地下水渗流服从达西定律，假设开挖后的隧道内壁(防水复合衬砌还未施工)均匀渗水，围岩内渗流方向以径向渗流为主。

3.3 计算模型

计算模型图如下：假定水面以下介质为围岩、注浆圈、衬砌。取水面为位势零面，水面高于地表围岩的深度为h，如果水位线低于地表，则h应取负值；为隧道中心埋深；为隧道注浆圈高度的一半；为注浆圈的厚度；如果不考虑注浆圈，可以将注浆圈与周围岩土体看成统一介质。

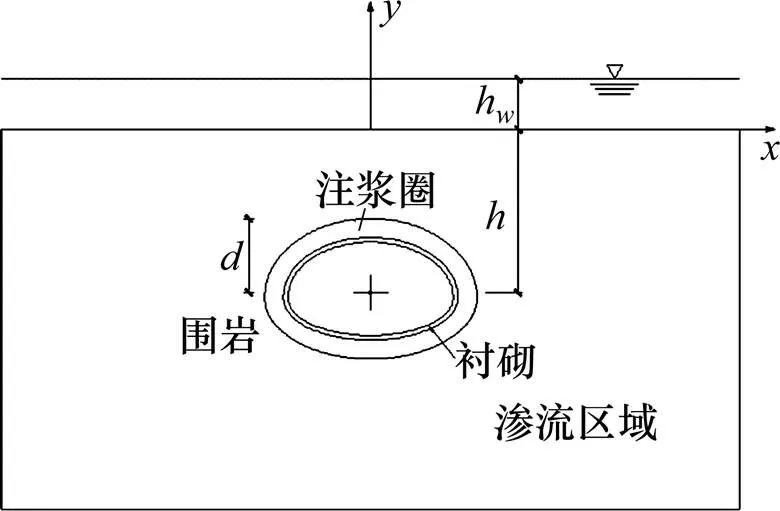
图4 马蹄形隧道计算模型示意图

本文考虑洞周水头为等水头条件，具体各个面的压力水头设置如图4中所示：0为隧道衬砌内壁的压力水头，如果考虑隧道不排水，则0=0，如果考虑隧道排水，则0≠0；1为衬砌与注浆圈交界面的压力水头；h为注浆圈与围岩界面的压力水头；h为水面高于或低于地表围岩的深度，即围岩表面的压力水头。需要注意的是，如果不考虑注浆圈，可以忽略1和2，仅考虑围岩中的压力水头与洞周的压力水头。

3.4 映射函数的确定

保角变换的原理主要是可以将复平面上的多连通区域通过几次变换变成单连通区域，从而达到简化拉普拉斯方程求解过程的目的。所以，问题的关键就是确定变换的映射函数。

将具体的变换步骤分为3次[8]：

1) 第1次变换(图6中(a)到(b))：

变换函数为

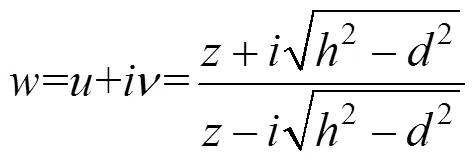
式中：z=x+iy，为渗流区域中的点集；d为隧道中心的在y方向的高度的一半；h为隧道高度中心距地面的深度。

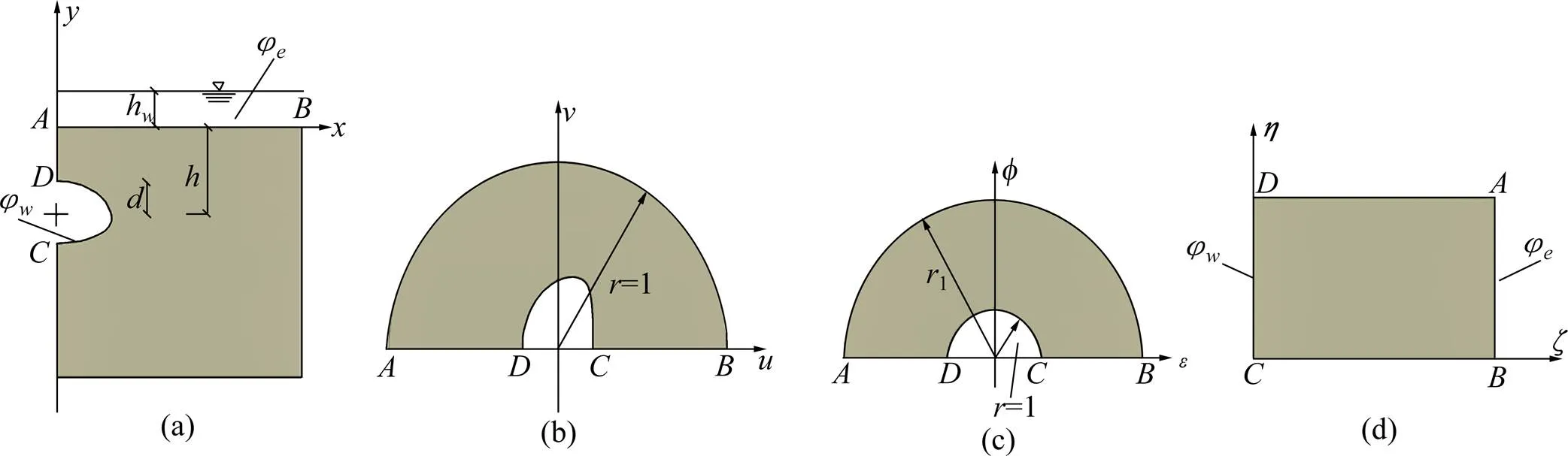
图6 几次保角变换示意图

2) 第2次变换(图4中(b)到(c))：

变换函数为

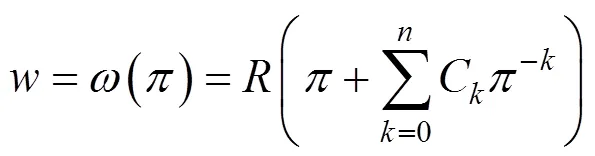
在平面中，当=1时，对应为隧道边界；=1时，对应为地表边界。

需要注意的是，第2次变换时需要展开成无穷级数项。计算理论上来说，系数的项数取得越多越准确，然而，实际情况中，考虑到计算的效率，只取前几项，同时不产生较大的相对误差，是一个比较适合的办法。根据前人的研究[9, 11]，对于半无限空间下的隧道，随着项数的增大，其绝对误差和平均误差也相应减小，则得到的映射函数更加精确。当≥6时，其映射精度变化很小，且误差与设计图形的几何尺寸相比基本可以不计。所以，计算时一般取6项即可满足需要的变换精度。

3) 第3次变换(图6中(c)到(d))：

变换函数为

通过3次保角变换，可以将半无限空间下马蹄形断面的隧道渗流问题转化为单连通矩形渗流 问题。

3.5 渗流场的确定

由假设条件可知，根据地下水渗流相关理论，可得矩形像平面中的势函数拉普拉斯方程：

其中：

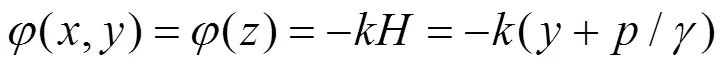
为势函数；为水头；为渗透系数；为孔隙水压；为水的容重。

解式(6)得：

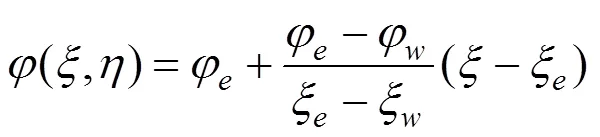
式中：，分别为图4中隧道边界边和地表边的势函数的数值；ξ和ξ分别表示在平面中隧道边界边和地表边的所对应的横坐标值，因此，联立式(1)~(5)进行变换，可得：

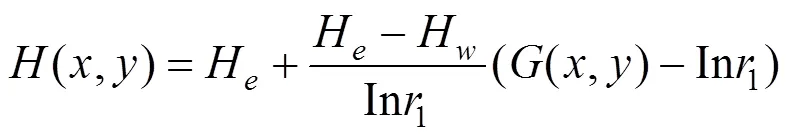
其中：水头可表示为：

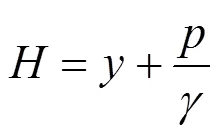
所以，联立式(9)~(10)，可以得到任意一点的孔隙水压力的解：

如果想得到渗流场Q可由单位渗流量的积分得到：

4 富水细粉砂岩隧道地下水渗流分析

基于第3节内容，可知只要明确隧道的基本几何外形参数、隧道所处的围岩体的基本岩土参数以及当地地下水渗流的基本特性参数，就可以将复杂形状断面的隧道地下水渗流问题简化并求解。

4.1 工程参数

根据3.1所提出的计算模型，为了降低计算难度，可以将太达村隧道实际马蹄形断面简化为“双椭圆形”，即由上下2部分椭圆合成。同时假设隧道未施作注浆圈，隧道断面稳定排水，具体的情况如图7所示。

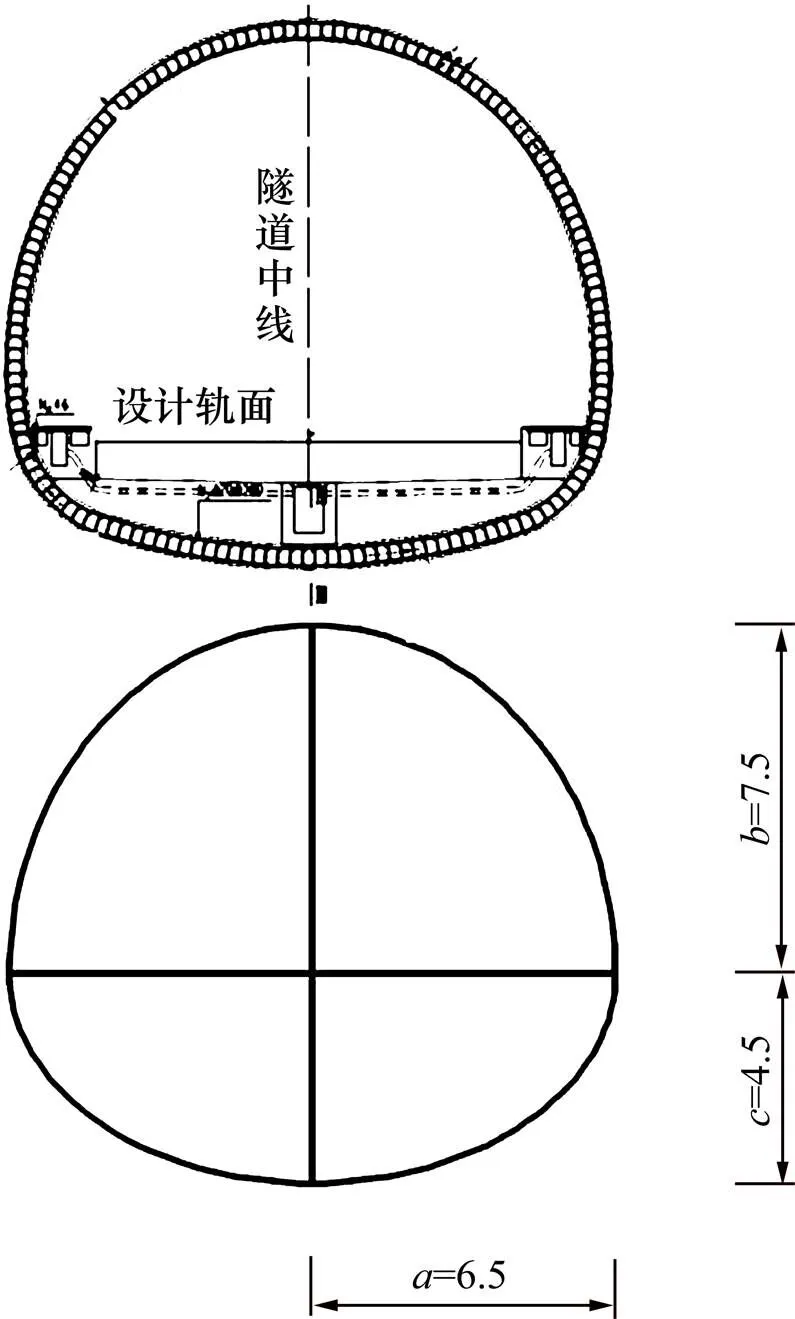
图7 隧道断面简化示意图

由图5可得，马蹄形隧道断面的基本几何参数为：=6.5 m，=7.5 m以及=4.5 m。

根据现场实际情况可知，DK241+760~DK241+ 760附近节理裂隙密集发育，围岩处于富水情况，发生涌水、涌沙可能性较大，故采用该段附近位置的隧道断面，考虑最不利情况，可以取以下参数：隧道中心距地表150 m，故拱顶埋深为=150−7.5= 142.5 m；地下水头根据实际勘察设定在地表以下130 m左右，为了计算取整，取地下137.5 m；细粉砂岩的渗透系数取k=2×10−4cm/s，孔隙率为0.5，流体体积模量为=2 GPa，流体密度为=103kg/m3。

4.2 计算结果

根据第3节推导的基本数学模型，结合4.1节中的工程参数，结合第3节中的变换函数以及渗流场计算公式，进行编程计算、绘图，可得到在等水头条件下的(即隧洞周边水头为等水头，地表水头为0且地下水位的水头一致)周围马蹄形隧道周围孔隙水压力分布的计算结果。

由图8和图9为本文所提出的方法所求出的解，取隧道中心向右水平延伸的孔隙水压力，由图中趋势可以看出，随着远离隧道中心线，孔隙水压力的变化值逐渐减小，最终趋近于一常数，约为1.34×103kPa。这一趋势较为合理，符合隧道地下水孔隙水压力的基本分布模式；同时，可以观察到，隧道外边缘(距隧道中心6.5 m处)的孔隙水压力为1.24×103kPa，孔隙水压力较大，需要进行相应的排水施工措施，否则会导致隧道断面以及掌子面的失稳。

图8 孔隙水压力和距离隧道中心水平距离关系

图9 隧道排水量和注浆圈厚度的关系

由图9可知，沿计算模型的纵向来看，随着计算模型中的深度逐渐加大，孔隙水压力也逐渐增大，并且整体呈线性趋势，这是由于隧道埋深较深，所以孔隙水压力整体呈线性趋势，在隧道断面拱顶处的孔隙水压力大小约为1.28×103kPa，拱底处约为1.40×103kPa，数值也较大，需要进行相应的超前排水降压措施，否则在施工过程中可能会出现失稳坍塌的现象。

5 支护及降水方案研究

以上渗流场分析研究结果表明太达村隧道富水细粉砂岩隧道施工段处于稳定渗流状态，且孔隙水压力较大，考虑到太达村隧道工程地质条件复杂，处理难度大，再加上工期紧张，为了保证工作面能够顺利推进，需要针对此特殊地质条件设计超前支护和降水方案。

5.1 主要问题

根据第2节中的基本围岩特性可知，太达村隧道的围岩状况比较特殊，在贫水段，粉砂岩整体的稳定性较好，使用常规开挖及支护措施即可确保施工进度。但是，在富水段，一旦粉细砂围岩受到开挖扰动，就会形成松动区域[12]，在此区域内由于孔隙增多，会加快该区域的渗流速度，使得该区域很快达到饱和的状态，围岩产生较大的塑性变形。最终，掌子面处开始出现涌水涌砂的现象，水质浑浊，呈泥浆状(见图10)，由于涌砂现象不断带走围岩中的土与砂粒，导致掌子面围岩稳定性难以维持，支护施工措施开展困难，工作面前进十分困难。国内外遭遇相似条件的隧道工程较少，仅有兰渝线胡麻岭[13]隧道施工中曾有过相似的工程地质条件，所以，进行此类特殊地质条件下隧道的支护降水措施的讨论是很有必要的，可以为未来类似条件的工程提供参考。

根据实际现场施工的实际情况，结合胡麻岭隧道施工的相关经验[12−13]，可以确定应采用超前支护与超前降水相结合的方式进行施工。

5.2 支护方案

对于支护方案，常见的方案有洞内帷幕注浆、洞内水平旋喷桩、地表垂直旋喷桩、管幕法、冷冻法和盾构法等。这些基本方法的基本优缺点如表1所示。

图10 隧道掌子面涌砂

表1 不同支护方法的优缺点对比

根据掌子面溜坍堆积物呈粉细砂状及钻孔涌泥沙情况，洞内水平旋喷桩是较为合适的方案之一。在太达村隧道中，拱墙可以采用f600水平旋喷桩超前加固，20 m一环，每循环搭接5 m，环向间距0.4 m，每环68根；掌子面水平旋喷加固间距2 m×2 m，每循环22根。为加强拱部水平旋喷桩抗弯刚度，内置f108钢管；上、中台阶锁脚处各设置一根旋喷桩，每处锁脚旋喷内置2根42钢管，布置示意图可见图11。

由于水平旋喷桩工艺复杂，成本较高，洞内操作难度较大，经多方讨论，确定以先采用洞内帷幕注浆的加固方式。在DK241+766~DK241+786施作一环全断面超前帷幕注浆加固，注浆长度30 m。注浆范围为开挖轮廓线外5 m，注浆采用水泥浆。由于岩质软弱，成孔困难，拱部采用前进式注浆，其余部位原则上采用后退式注浆，具体布置可见图12(a)。最终，本段共计注浆钻孔个数182个，补充注浆孔11个，注浆总长度4 782 m。本循环帷幕注浆量总计2 122 m3，每延米注浆量0.44 m3。设置6个验证孔以验证注浆效果，现场实际施作5孔，其中取芯4孔，孔内成像1孔见(图12(b))。最终，经专家效果评估，帷幕注浆施工效果明显，基本满足设计要求，可以进行下一步施工。

图11 水平旋喷桩布置图

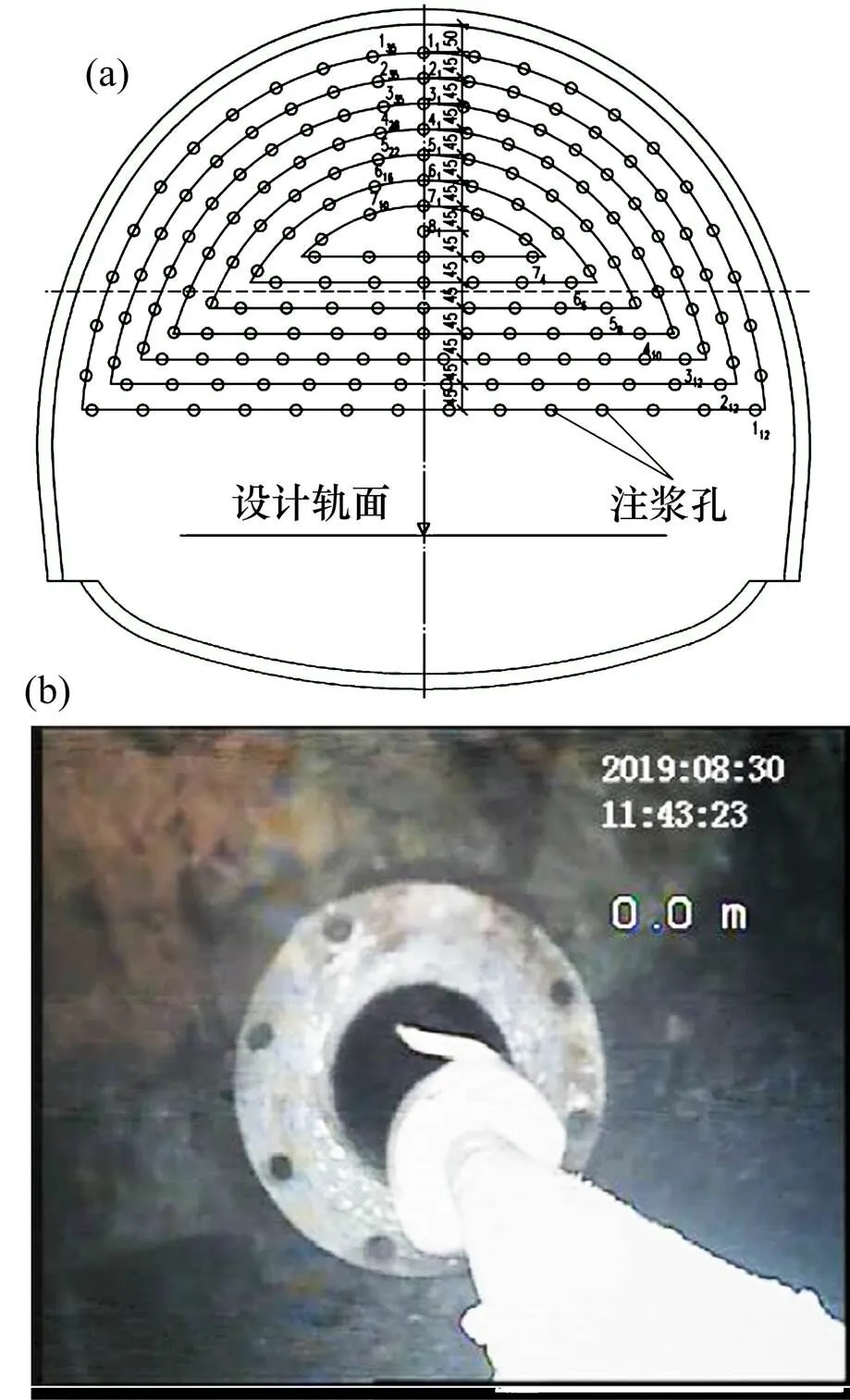
(a) 帷幕注浆布置图；(b) 检查孔孔内成像图

5.3 降水方案

由于隧道所处的富水粉细砂岩水稳性极差，据现场勘测，一般掌子面开挖后4～6 h掌子面开始发生流变，6 h以后掌子面失稳，故需要及时采取降水措施保证粉细砂岩含水率保持在合理含水率以内，确保施工安全。

对于降水方案，常见的方案有地表深井降水、洞内全断面降水等。由前文的渗流分析可知，目前太达村隧道粉细砂地层为弱渗透性地层，且根据现场钻孔显示地层为泥岩、砂岩互层状，预计地表降水较难发挥工效，故洞内全断面降水是比较合理的选择。结合实际情况，具体可按图13方法实行：在上、中台阶下50 cm处布设4 m长真空降水管，沿水平方向打设，水平间距1 m，对掌子面前方进行真空降水；同时在隧道侧壁各台阶拱脚向下外插打斜向降水管，长度4 m每根，纵向间距0.75 m，外插角30度；最后在沿隧底两侧布置重力真空深井降水管，在隧底离边墙1.5 m处埋置深于仰拱基底10~12 m的井管，梅花形布置，通过潜水泵将地下水抽出，使地下水位低于坑底。实践表明，全断面降水可以取得较好的效果，可以抑制掌子面涌水涌砂的现象。

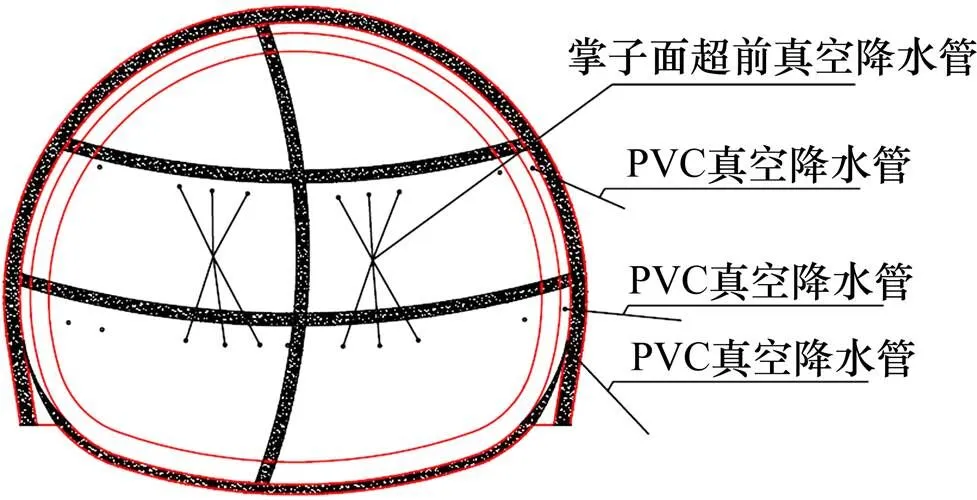
图13 全断面降水布置图

6 结论

1)在文献[11]的基础上，利用保角变换，推导山岭隧道中马蹄形隧道在地下水稳定渗流作用下渗流场的解，为复杂形状断面隧道的渗流场求解问题提供可靠的解决方法。

2) 以太达村富水粉细砂岩层隧道渗流问题为工程实例，利用提出的模型求解地下孔隙水压力分布的结果，为超前排水工程提供指导。

3) 针对太达村隧道工程的特殊地质条件，分析几种主要的支护、降水方案的优缺点，并结合实际条件提出可靠合理的的超前降水支护方案。

[1] 毕焕军. 胡麻岭隧道水敏性砂岩地下水渗流场模拟研究[J]. 铁道工程学报, 2013(12): 64−68. BI Huanjun. Research on the seepage field simulation of water-sensitive sandstone in Humaling tunnel[J]. Journal of Railway Engineering Society, 2013(12): 64−68.

[2] Verruijt A. Complex variable solution for a deforming circular tunnel in an elastic half-plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2): 77−89.

[3] Huangfu M, WANG M S, TAN Z S, et al. Analytical solutions for steady seepage into an underwater circular tunnel[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 391−396.

[4] 王秀英, 王梦恕, 张弥. 计算隧道排水量及衬砌外水压力的一种简化方法[J]. 北方交通大学学报, 2004, 28(1): 8−10. WANG Xiuying, WANG Menshu, ZHANG Mi. Simple method to calculate tunnel discharge and external water pressure on lining[J]. Journal of Northern Jitaotong University, 2004, 28(1): 8−10.

[5] Goodman R E , Moye D G . Ground water inflows during tunnel driving[J].  Engineering Geology, 1965, 2: 35−56.

[6] Freeze R A , Cherry. Groundwarer[M]. Englewwood, New Jersey: Prentice-Hall Inc, 1979.

[7] LEI S. An analytical solution for steady flow into a tunnel[J]. Ground Water, 1999, 37(1): 23−26.

[8] 拉普伦捷夫. 复变函数论方法[M]. 北京: 人民教育出版社, 1956.Лаврентьев. Methods of functions of a complex variable [M]. Beijing: People’s Education Press, 1956.

[9] 吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007. LÜ Aizhong, ZHANG Luqing. Complex function method for mechanical analysis of underground tunnel[M]. Beijing: Science Press, 2007.

[10] 蔚立元, 陈晓鹏, 韩立军, 等. 基于复变函数方法的水下隧道围岩弹性分析[J]. 岩土力学, 2012(增2): 345− 351. WEI Liyuan, CHEN Xiaopeng, HAN Lijun, et al. Elastic analysis of surrounding rock for underwater tunnels based on functions of complex variables method[J]. Rock and Soil Mechanics, 2012(Suppl 2): 345−351.

[11] 莫海强. 水下任意形状断面隧道稳定渗流场研究[D].长沙: 中南大学, 2018. MO Haiqiang. Study on steady seepage field of underwater tunnel with arbitrary shape section[D]. Changsha: Central South University, 2018.

[12] 曹峰. 兰州第三系砂岩水稳性特征隧道施工研究[J]. 铁道工程学报, 2012, 29(12): 21−25, 31. CAO Feng. Special research on water-stability characteristics of tertiary system sandstone in Lanzhou area during tunnel construction[J]. Journal of Railway Engineering, 2012, 29(12): 21−25, 31.

[13] 毕焕军. 胡麻岭隧道第三系富水砂岩地表深井降水研究[J]. 铁道标准设计, 2015, 59(7): 116−119. BI Huanjun. Research on surface dewatering with deep well in tertiary water-rich sandstone of Humaling tunnel [J]. Railway Standard Design, 2015, 59(7): 116−119.

Study on groundwater seepage characteristics and reinforcement scheme oftunnels surrounded by water-rich fine siltstone rock

LI Xiaofeng

(The 5th Company of the China Railway 18th Bureau Group Co., Ltd, Tianjin 300459, China)

One construction section of the Yumo railway tunnel located in the Taida Village is mainly surrounded by fine siltstone. The excavation disturbance or the occurrence of sand gushing in the presence of water will rapidly deteriorate the mechanical properties of the rock masses and affect the construction progress. To study the seepage characteristics of groundwater in water-rich siltstone tunnels, based on the complex variable function method in the stability analysis of the surrounding rock of the underground tunnel, the shape transformation function of the actual horseshoe tunnel and the numerical solution of tunnel seepage field during the process of excavation were obtained. Compared with the analytical solution of seepage in traditional circular tunnels, this proposed method has higher prediction accuracy. Finally, in combination with the prediction of the analytical solution and the in-situ engineering geological conditions, the rationality of several reinforcement schemes and water-lowering methods were analyzed.

tunnel; seepage characteristics; fine siltstone; complex variable function; groundwater

10.19713/j.cnki.43−1423/u.T20200038

U45

A

1672 − 7029(2020)07 −1799 − 09

2020−01−12

国家科技重大专项资助项目(2017YFB1201200)

李小丰(1976−)，男，天津人，高级工程师，从事铁路工程施工管理及研究工作；E−mail：756855722@qq.com

(编辑 蒋学东)