地震作用下超高墩三塔大跨斜拉桥结构体系比选研究

徐向东，魏标，马白虎，杜镔，刘兴茂

地震作用下超高墩三塔大跨斜拉桥结构体系比选研究

徐向东1，魏标2，马白虎3，杜镔1，刘兴茂3

(1. 贵州省交通规划勘察设计研究院股份有限公司，贵州 贵阳 550081；2. 中南大学 土木工程学院，湖南 长沙 410075；3. 贵州省公路开发有限责任公司，贵州 贵阳 550081)

为探究超高墩三塔大跨斜拉桥的合理结构体系，以在建的贵州平塘特大桥为工程背景，建立3种结构体系的有限元模型(原体系、半漂浮体系FS和塔梁固结体系RS)，并对3种体系自振特性进行简要分析。研究3种结构体系在多维地震作用下内力响应和位移响应的差异性。基于OPENSEES和概率地震需求理论对3种结构体系进行地震易损性分析。研究结果表明：在横向+竖向地震作用下，3种结构体系的内力响应和位移响应都相差不大；在纵向+竖向地震作用下，原结构体系的内力响应和位移响应介于FS体系和RS体系之间，更为合理；2个边塔在RS体系中发生轻度损伤的概率最大，中塔在原结构体系中发生轻度损伤的概率最大，相比于FS体系和RS体系，原结构体系更加合理。

桥梁工程；方案比选；超高墩三塔斜拉桥；IDA；非线性时程分析

斜拉桥不同体系间受力方式存在较大差别。目前对于斜拉桥不同体系间比选的研究相对较少，且对山区超高墩三塔斜拉桥的比选研究更是鲜有，故开展三塔斜拉桥地震响应与结构比选的研究很有必要。关于斜拉桥地震响应的研究，国内外学者也开展了许多工作[1]。20世纪70年代，日本在兴建本州四国联络线时，对斜拉桥的地震响应进行了大量的研究，并制定了相应的设计规范[2]。与此同时，美国也对斜拉桥的抗震性能进行了大量的数值分析与实验研究。Shehata[3]对横向地震作用下斜拉桥的地震响应控制提出了一种简便方法。HAN等[4]提出了一种基于直接位移的基础隔震斜拉桥横向地震设计方法。Nazmy等[5−6]对某大跨斜拉桥进行了线性和非线性地震响应分析。Bipin等[7−10]分别对Karnali斜拉桥、武汉军山长江大桥、某漂浮体系斜拉桥和沪通长江大桥的地震响应规律进行了系统的研究。基于上述研究，本文以贵州平塘特大桥为研究对象，基于SAP2000和OPENSEES软件平台，建立多非线性3种有限元模型(原体系、半漂浮体系FS和塔梁固结体系RS)，从结构动力特性、地震响应和结构易损性3个方面对比研究3种体系相对差异性。

1 工程背景及有限元模型

1.1 工程背景

贵州平塘特大桥为三塔双索面钢混叠合梁斜拉桥，主桥跨径为249.5 m+550 m+550 m+249.5 m，墩塔布置如图1(a)所示，其中15～17号为主塔，14号和18号为两侧辅助墩，13号为过渡墩，19号为桥台。主梁横断面如图1(b)所示。索塔下横梁以上塔高均为145.2 m，下横梁以下15～17号索塔分别为174.8，186.8和152.8 m，全高分别为320，332和298 m，其中，中塔(16号塔)为世界第一高混凝土桥塔。全桥共设264根斜拉索，扇形布置。斜拉索采用低松弛镀锌高强钢丝，直径7 mm，抗拉强度标准值pk=1 770 MPa。

1.2 有限元模型

利用SAP2000建立平塘特大桥全桥有限元模型。主梁、主塔及桥墩均采用空间梁单元进行模拟，主梁采用双主纵梁模型。桥面板采用板单元进行模拟，斜拉索采用拉索单元进行模拟，并考虑斜拉索的-Δ效应。桥面铺装、栏杆以及后期压重等作为二期恒载考虑，并将其转化为质量。建立模型时考虑桩−土−结构的相互作用，采用m法计算出承台底的桩−土弹簧作用。

平塘特大桥原结构体系为中塔塔梁铰接，边塔竖向支承。为比较不同结构体系在地震作用下的响应，分别建立平塘特大桥半漂浮体系(FS)和塔梁固定铰支撑体系(RS)有限元模型。FS体系在墩梁、塔梁连接处均设置单向纵向活动支座；RS体系在墩梁连接处设置单向纵向活动支座，在塔梁连接处采用固定铰支座，约束纵向和横向位移，3种体系下支座布置示意图如图2所示，有限元模型如图2(d)所示。

2 不同体系结构动力特性分析

表1列出了3种体系前8阶自振频率及相应的振型特征。通过对比表1可以发现：

1) 3种结构体系的第1阶振型相同，但频率差异较大，FS基频最小，RS基频最大。

2) 原结构体系与RS体系前8阶振型基本一致。原结构体系在第7阶振型为主梁1阶对称竖弯，第8阶振型为主梁1阶对称横弯，而RS体系则是在第7阶先出现主梁1阶对称横弯，与原结构体系恰好相反。此外，原结构体系每一阶的频率几乎都小于RS体系。

3) 综合以上结论可以预测：在纵向地震作用下RS体系会有最大的内力响应，FS体系会有最大的位移响应，而在横向地震作用下3种结构体系的地震响应较为接近。

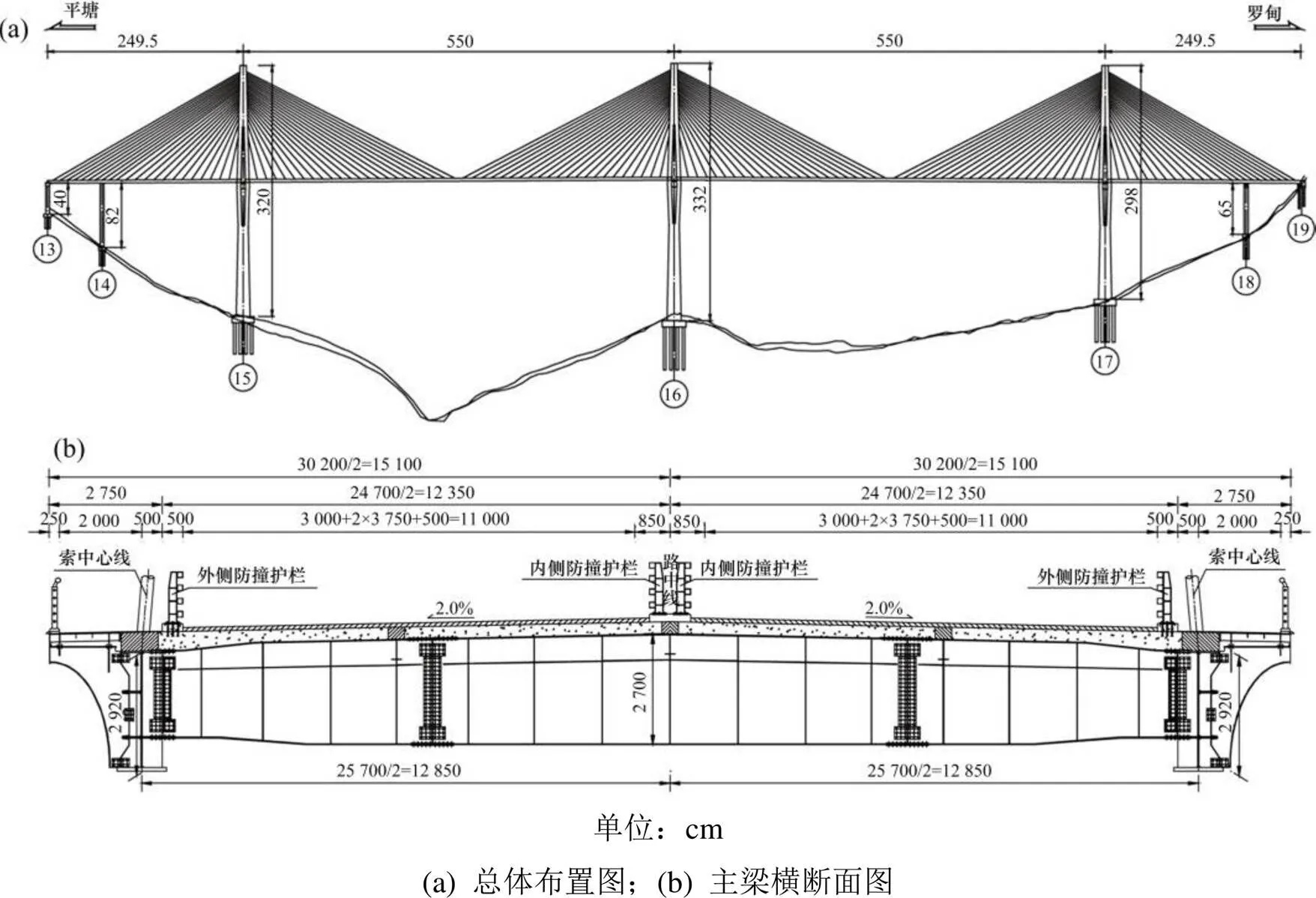
图1 总体布置图与主梁横断面图

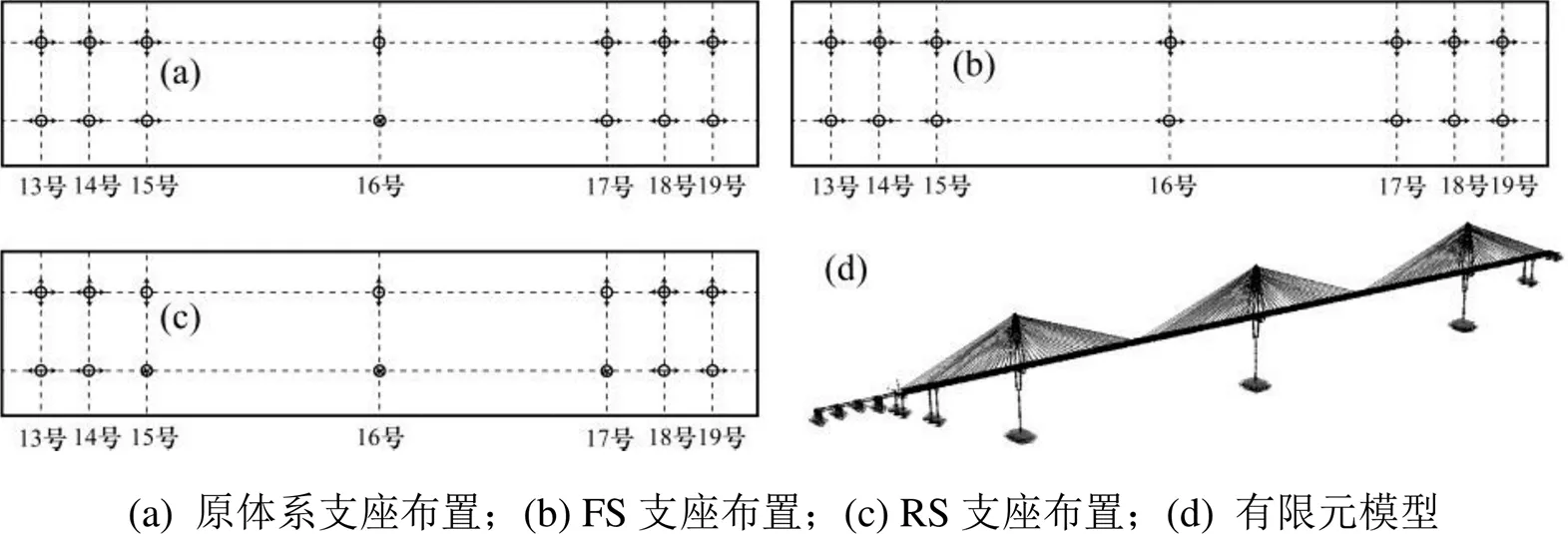
图2 支座布置及有限元模型

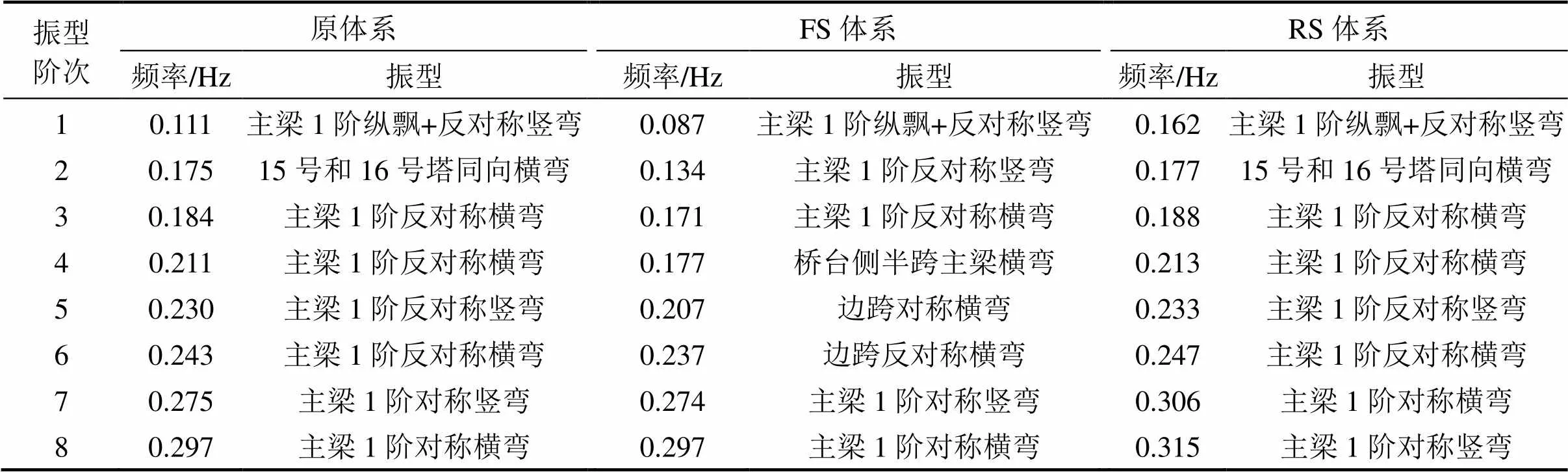
表1 3种结构体系自振特性

3 不同体系响应对比分析

选用平塘特大桥地震安全性评价报告[11]中提供的加速度时程数据，每个地震水平对应3条人工地震波。取3条地震波激励下结构地震响应的最大值进行对比分析。地震波的输入方式采用纵向+竖向(简称纵向)地震和横向+竖向(简称横向)地震2种组合，竖向加速度值取2/3的水平向加速度值，3条人工地震动曲线如图3所示。每个地震水平对应3条人工地震波，每条地震波包含4 096个加速度时程数据，时间间隔为0.02 s。

图3 人工地震动时程曲线

3.1 结构内力响应对比

表2给出了3种不同体系在纵向地震和横向地震作用下主塔塔底弯矩的对比结果。

由表2可知：1) 在E1地震纵向作用下，RS体系15号和17号主塔的塔底弯矩分别比原结构大66.7%和53.3%，在E2地震作用下，RS体系17号主塔的塔底弯矩仅比原结构体系大15.1%；原结构体系15号主塔的塔底弯矩分别比FS和RS大30.3%和小6.03%；FS体系和RS体系16号主塔的塔底弯矩分别为原结构体系的76.7%和77.1%。

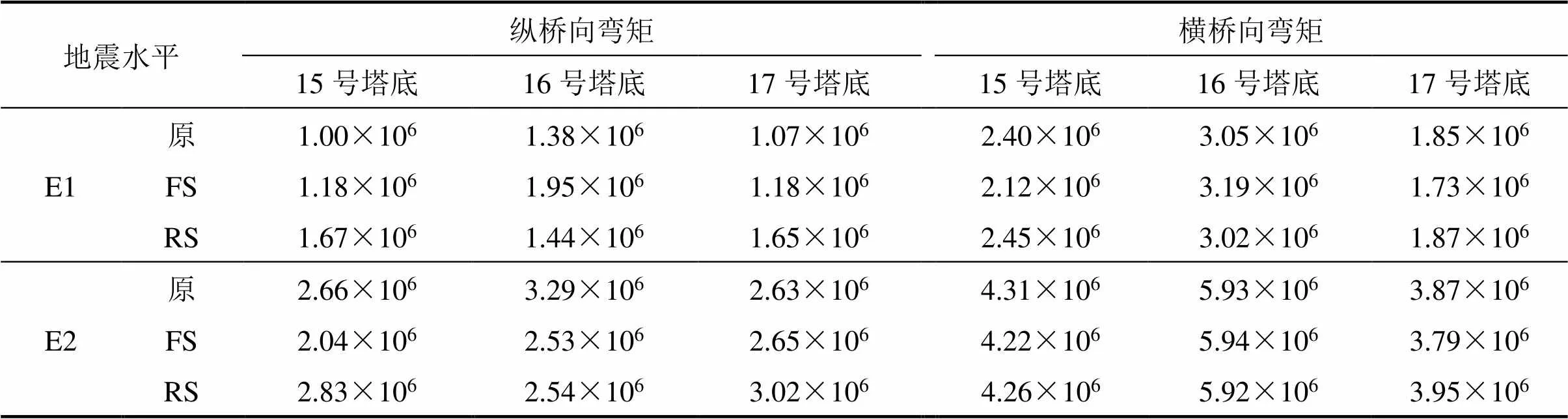
表2 塔底弯矩

2) 在E1横向地震作用下，原体系15号塔底弯矩比FS体系大13.2%，比RS体系小2.0%；原体系16号的塔底弯矩比FS体系小4.4%，比RS体系大1.1%；17号塔底弯矩比FS体系大6.8%，比RS体系小1.0%。而在E2地震作用下，3种体系主塔塔底弯矩的差异均不超过2%。

3.2 结构位移响应对比

图4和图5分别给出了3种不同结构体系在纵向地震和横向地震作用下主梁位移。

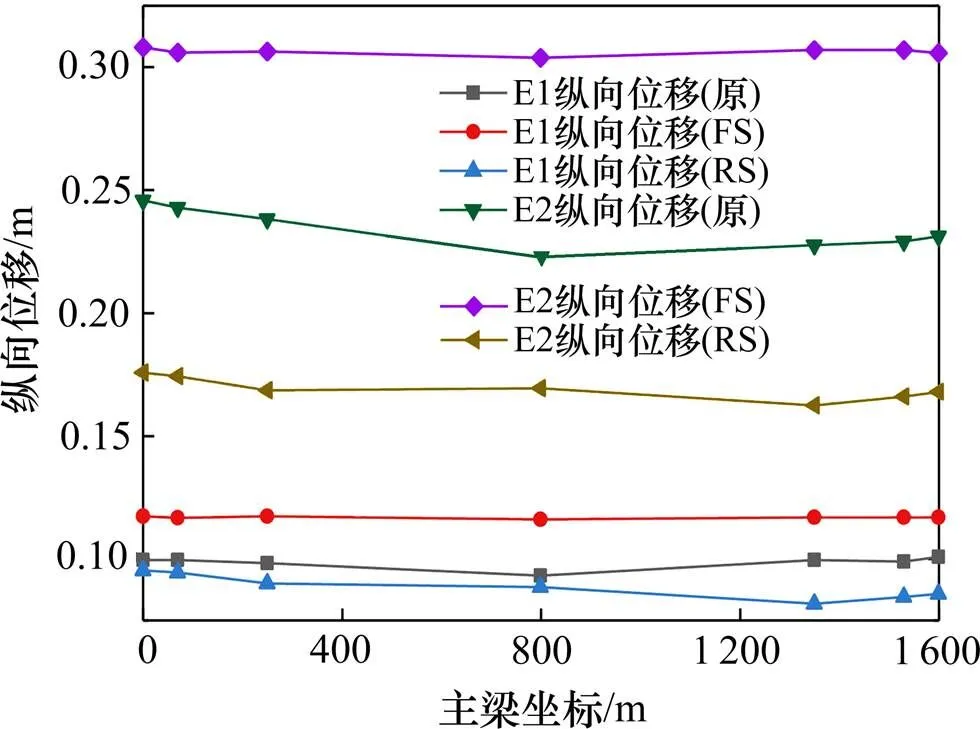
图4 主梁纵向位移(纵向地震)

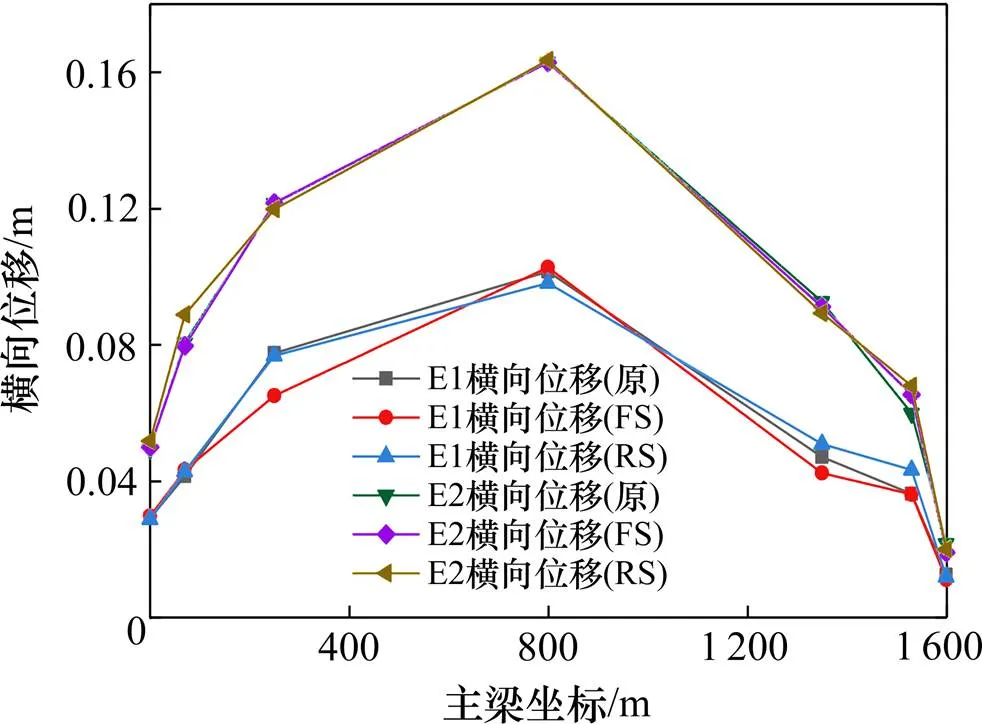
图5 主梁横向位移(横向地震)

由图4和图5可知：在纵向地震作用下，RS体系主梁的纵向位移最小，FS体系主梁的纵向位移最大。具体而言，FS体系主梁的纵向位移比原结构体系大16.0%~36.3%，RS体系主梁的纵向位移比原结构体系小4.1%~29.2%；

在横向地震作用下，3种结构主梁的横向位移基本相同，尤其在E2地震作用下，3种结构主梁的横向位移几乎完全吻合。

4 不同体系易损性对比研究

平塘特大桥纵向振动与横向振动基本不耦合，3种结构体系在横桥向支座约束一致，进行3种体系在横向地震作用下的易损性曲线对比意义不大，故本文基于概率性地震需求模型构建桥梁理论易损性曲线[12−13]，并只进行了不同结构体系在纵桥向地震作用下的易损性对比。

4.1 易损性地震动确定

利用《公路桥梁抗震设计细则》计算桥址工程场地水平向设计反应谱曲线，以此为目标谱导入PEER强震记录数据库，选取平均反应谱曲线跟目标反应谱拟合程度最好的20条地震记录作为地震动输入(如图6所示)，以此进行增量动力分析。采用纵向+竖向地震组合，竖向加速度值取2/3的水平向加速度值。

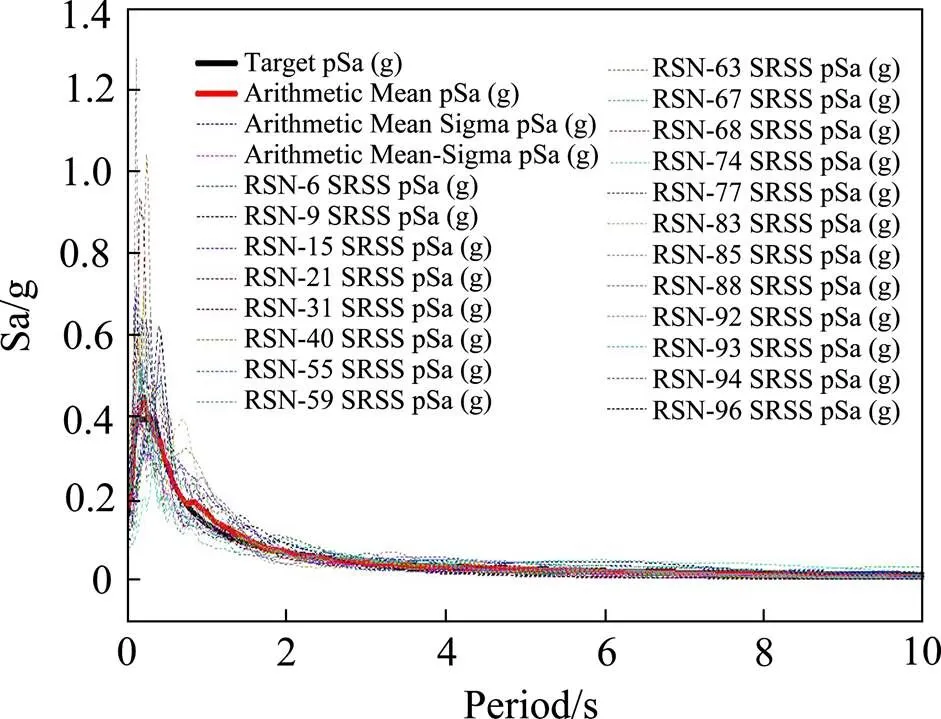
图6 地震动输入

4.2 地震易损性指标确定

将系统中每个构件的损伤状态分为完好无损、轻度破坏、中度破坏、严重破坏和完全破坏5种类别。抗震能力为5个损伤状态间的4个界限值，分别为：完好无损至轻度破坏、轻度破坏至中度破坏、中度破坏至严重破坏、严重破坏至完全破坏状态。

根据Kowalsky和Priestly的研究成果，通过材料应变来确定构件的破坏状态。桥墩和桩基的材料应变采用保护层混凝土的应变值，如表3所示。桥梁支座采用相对位移作为损伤指标。该桥支座位移量设计为±100 mm，因此定义轻微破坏和完全破坏的性能分别为100 mm和200 mm，同时基于延性破坏准则并结合支座的本构关系，根据实际经验确定其损伤状态界限值，支座损伤状态具体如表3所示。

表3 构件损伤指标

4.3 主塔易损性分析

平塘特大桥桥塔采用箱型变截面，各关键截面编号如图7所示。限于篇幅，本文只给出各构件易受损部位曲线。

图7 主塔关键截面位置及编号

图8~10分别给出了3种不同结构在纵向地震下主塔易受损截面(下横梁塔下截面sec5和距塔底6.5 m处截面sec10)保护层混凝土轻度破坏的易损性曲线。

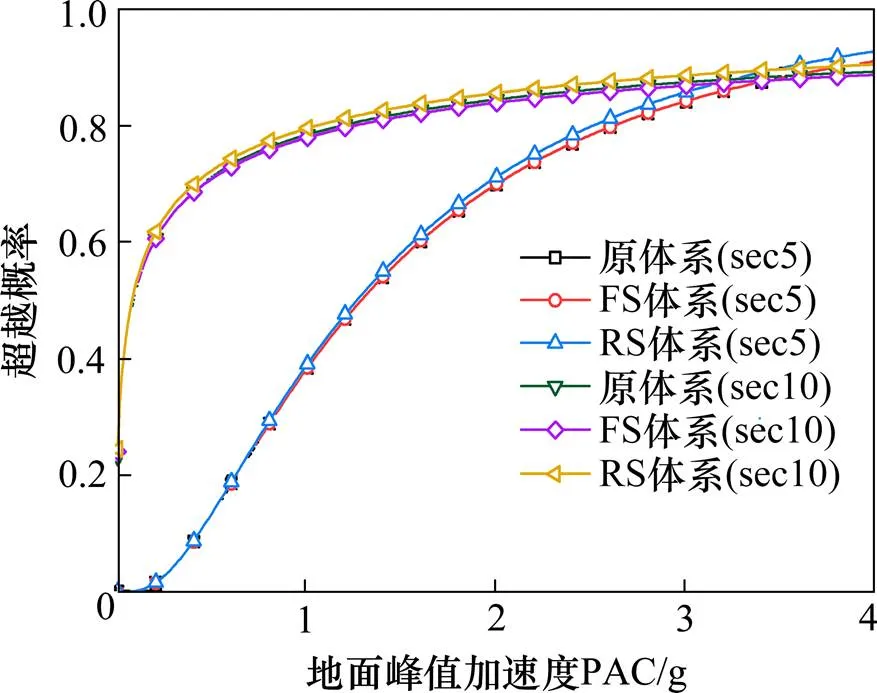
图8 15号塔易损性曲线

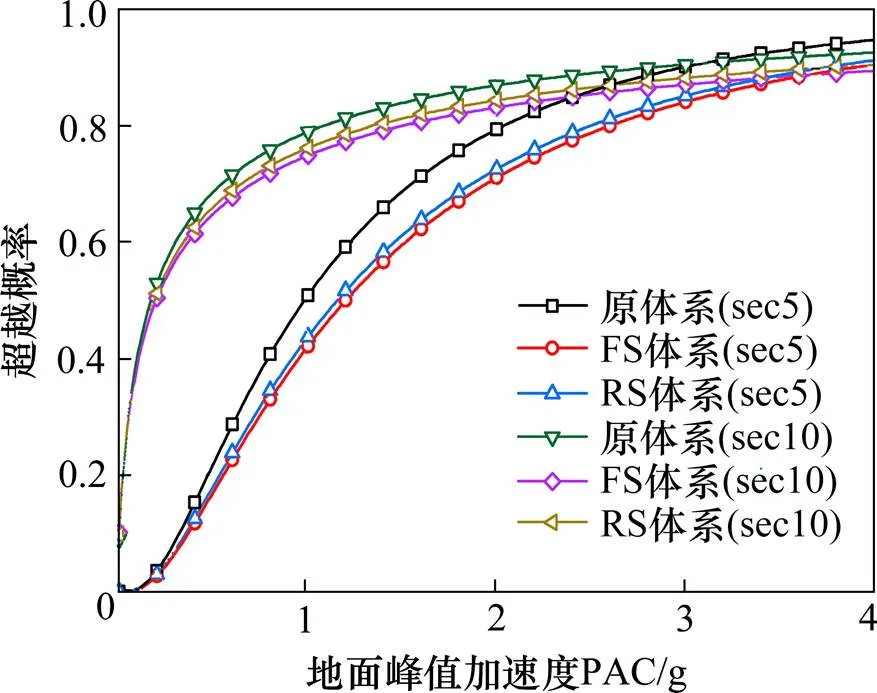
图9 16号塔易损性曲线

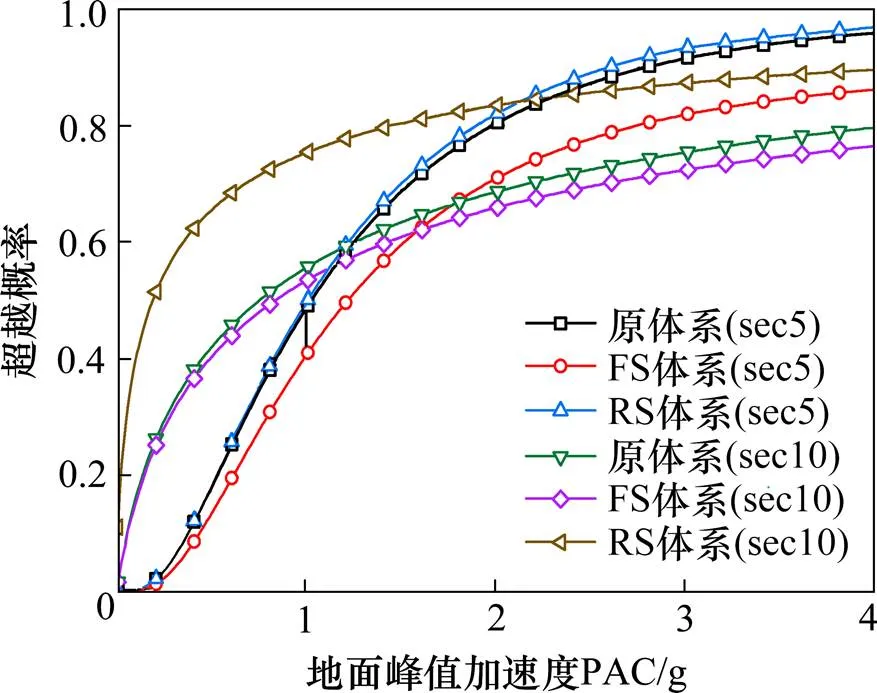
图10 17号塔易损性曲线

由图8~10可以看出：

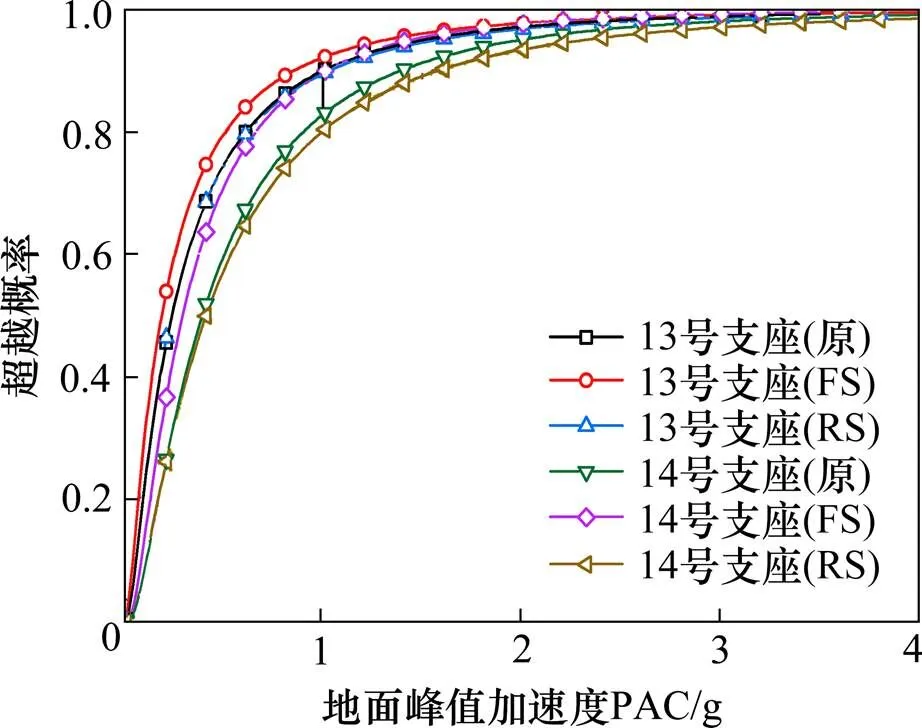
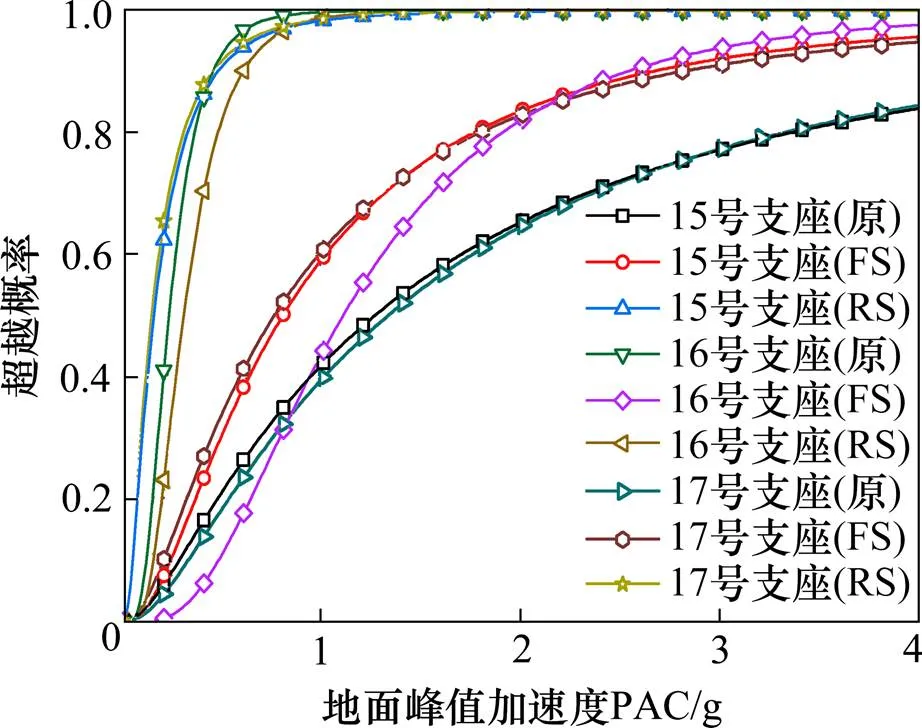
1) 针对15号塔，当0

2) 针对16号塔，当PGA<0.2时，3种体系下sec5和sec10截面保护层混凝土发生轻度损伤的概率基本相近；当PGA>0.2时，原结构体系中16号塔发生损伤概率最大，FS体系最小；原结构体系截面sec5和sec10截面保护层混凝土发生轻度损伤的概率比FS结构体系分别大4.47%和3.37%。

3) 针对17号塔，当0

4) 在纵向+竖向地震作用下，RS体系中15号和17号塔截面保护层混凝土发生轻度损伤的概率最大，原结构体系中16号塔截面保护层混凝土发生轻度损伤的概率最大。

4.4 支座易损性分析

限于篇幅，仅给出完全破坏状态下3种体系在纵向+竖向地震下各支座沿纵桥向的地震易损性曲线。由于结构体系对称，仅列出靠近平塘一侧过渡墩和辅助墩支座(13号墩支座和14号墩支座)的易损性曲线。

分析图11和图12可知，13号和14号支座受损程度从高到低依次为FS,原体系和RS。图12表明RS体系时15号塔和17号塔支座纵向更易受损，是因为RS体系将原结构中相应位置处的滑动支座改为固定支座。而纵向地震作用下固定支座比滑动支座更易受损，故呈现出固结体系下两边塔支座更易受损的现象。根据图12，FS体系16号塔支座受损伤概率最低，因为16号塔支座沿纵桥向为滑动支座，而原设计体系和RS体系在该支座处均为固定支座，故该体系下支座最迟破坏。

图11 13号至14号支座易损性曲线

图12 15号至17号支座易损性曲线

5 结论

1) 3种结构体系的第1阶振型相同，但频率差异较大，FS体系的基频最小，RS体系的基频最大。原结构体系每一阶的频率几乎都小于RS体系，原结构体系每一阶的频率几乎都大于FS体系。

2) 在横向+竖向地震作用下，3种结构体系的内力响应和位移响应相差不大。在纵向+竖向地震作用下，原结构体系的内力响应和位移响应恰好介于FS体系和RS体系之间，且主塔塔底弯矩没有出现16号中塔小于边塔的现象，更为合理。

3) 地震作用下，RS体系中两边塔发生轻度损伤的概率最大，原体系中塔发生轻度损伤的概率最大，但仅比FS分别大4.47%和3.37%；FS体系中桥墩支座发生损伤概率最大。也即地震作用下相比于FS体系和RS体系，原结构体系是最优方案。

[1] 秦红禧. 高速铁路大跨度钢桁梁斜拉桥地震响应研究及减震分析[D]. 长沙: 中南大学, 2011.QIN Hongxi. Seismic response research and seismic reduction analysis of long-span steel truss cable-stayed bridge on high-speed railway[D]. Changsha: Central South University, 2011.

[2] 王爱国. 大跨度斜拉桥动力特性及抗震性能分析[D].武汉: 武汉理工大学, 2008.WANG Aiguo. Dynamic characteristics and seismic performance analysis of long-span cable-stayed bridges[D]. Wuhan: Wuhan University of Technology, 2008.

[3] Shehata E Abdel Raheem. Structural control of cable- stayed bridges under traveling earthquake wave excitation[J]. Coupled Systems Mechanics, 2018, 7(3): 269−280.

[4] HAN Qiang, WEN Jianian, DU Xiuli, et al. Simplified seismic resistant design of base isolated single pylon cable-stayed bridge[J]. Bulletin of Earthquake Engineering, 2018, 16(10): 5041−5059.

[5] Nazmy H H, AbdEl-Ghaffar A M. Non-linear earthquake response analysis of long-span cable-stayed bridge application[J]. Earth Engineering Structure Dynamics, 1990, 19(11): 63−76.

[6] GUAN Zhongguo, YOU Han, LI Jianzhong. An effective lateral earthquake-resisting system for long-span cable-stayed bridges against near-fault earthquakes[J]. Engineering Structures, 2019, 196(1):1−14 .

[7] Bipin Shrestha. Seismic response of long span cable-stayed bridge to near-fault vertical ground motions [J]. Structural Engineering, 2015, 19(1): 180−187.

[8] 徐凯燕, 魏德敏. 武汉军山长江大桥非线性地震反应时程分析[J]. 湖南大学学报(自然科学版), 2010, 37(5): 19−23. XU Kaiyan, WEI Demin. Nonlinear seismic response time history analysis of Junshan Yangtze river bridge in Wuhan[J]. Journal of Hunan University (Natural Sciences), 2010, 37(5): 19−23.

[9] MA Kai, ZHONG Jian, FENG Ruiwei, et al. Investigation of ground-motion spatial variability effects on component and system vulnerability of a floating cable-stayed bridge[J]. 2019, 22(8): 1923−1937.

[10] 屈爱平, 李龙安. 沪通长江大桥主航道桥抗震设计[J].桥梁建设, 2015, 45(6): 69−73.QU Aiping, LI Longan. Seismic design of main ship channel bridge of Hutong Changjiang river bridge[J]. Bridge Construction, 2015, 45(6): 69−73.

[11] 武汉地震工程研究院有限公司. 贵州省余庆至安龙高速公路平塘至罗甸段平塘特大桥工程场地地震安全性评价报告[R]. 武汉: 2015. Wuhan Institute of Earthquake Engineering Co.Ltd. Seismic safety assessment report of Pingtang Bridge project site in Pingtang-Luodian Section of Yuqing- Anlong Expressway in Guizhou Province[R]. Wuhan: 2015.

[12] 郑凯锋, 陈力波, 庄卫林, 等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学, 2013, 30(5): 165−171, 187. ZHENG Kaifeng, CHEN Libo, ZHUANG Weilin, et al. Bridge vulnerability analysis based on probabilistic seismic demand model[J]. Engineering Mechanics, 2013, 30(5): 165−171, 187.

[13] YANG Xiang, YONG Feng, LUO Qinglong, et al. Probabilistic inelastic seismic demand spectra for large-span planar steel structures subjected to vertical ground motions[J]. Engineering Structures, 2018, 171(1): 646−662.

Study on structural system selection of three-tower long-span cable-stayed bridge with high piers under earthquake

XU Xiangdong1, WEI Biao2, MA Baihu3, DU Bin1, LIU Xingmao3

(1. Guizhou Transportation Planning Survey and Design Academe Co. Ltd, Guiyang 550081, China;2. School of Civil Engineering, Central South University, Changsha 410075, China;3. Highway Administration Bureau of Guizhou Province, Guiyang 550081, China)

In order to explore the reasonable system of three-pylon cable-stayed bridges with high piers and large span in mountainous areas, taking Pingtang super-large bridge in Guizhou as the engineering background, three finite element models (original system, semi-floating system FS and Tower-girder consolidation system RS) were established based on SAP2000, and the natural vibration characteristics of the three systems were briefly analyzed. Secondly, the differences of internal force response and displacement response of the three systems under multi-dimensional earthquake were studied. Finally, based on OPENSEES and probabilistic seismic demand theory, three vulnerability models were established to analyze the vulnerability of bridge towers and other important components. The results show that the internal force and displacement responses of the three structural systems are almost the same under lateral and vertical earthquake action. Under the action of longitudinal and vertical earthquake, the internal force and displacement responses of the original structure system are just between FS system and RS system, which is more reasonable. Side towers have the greatest probability of slight damage in RS system, and middle towers have the greatest probability of slight damage in the original structure system. Compared with FS system and RS system, the original structure has the greatest probability of slight damage. The system is a more reasonable scheme.

bridge engineering; scheme selection; three-pylon cable-stayed bridge with high piers; IDA; nonlinear time history analysis

10.19713/j.cnki.43−1423/u.T20190794

U448.27

A

1672 − 7029(2020)07 − 1743 − 08

2019−09−06

国家自然科学基金资助项目(51778635)；贵州省重大科技专项计划资助项目(黔科合重大专项字[2016]3013)；湖南省自然科学基金资助项目(2019JJ40386)

魏标(1982−)，男，江苏铜山人，教授，博士，从事桥梁抗震研究；E−mail：weibiao@csu.edu.cn

(编辑 涂鹏)