基于改进粒子群算法的鸡蛋裂纹检测方法
张 健 崔英杰
(黄淮学院,河南 驻马店 463000)
目前鸡蛋裂纹检测方法主要分为有损检测、无损检测。声波信号(AS)是典型的有损检测方法[1],虽然检测速度比较快,但是蛋壳在检测中由于受到了机械振动,很容易产生二次破裂。无损检测通过采集鸡蛋图像进行外部检测,不会对鸡蛋产生破坏,主要方法有:① 利用神经网络(Neural Network,NN)对分割出的鸡蛋裂纹图像区域识别,该法准确率较高,并且泛化功能和鲁棒性较好[2],但对微小裂纹检测时正确率较低;② 利用鸡蛋图像纹理特征(ITF)对鸡蛋裂纹进行检测[3],与神经网络算法相比方法相对简单,但对复杂裂纹不易检测;③ 小波模极大值法(WMM)对裂纹明显的边缘能达到较好的效果[4],但会丢失鸡蛋裂纹的弱边缘信息;④ 遗传算法(GA)通过遗传编码提高了裂纹区域范围较大的检测准确度[5],但易将噪声误判为鸡蛋裂纹边缘;⑤ 均值聚类(MC)算法实现较简单[6],但对灰度幅值较小的鸡蛋裂纹检测存在图像边缘不连续,导致断开现象发生。
粒子群(PSO)算法具有可调参数少,可以全局搜索最优解等优点,有研究学者[7]使用粒子群神经网络方法识别种蛋成活性,但是粒子群算法对鸡蛋裂纹检测还未见报道。为了使该方法适用于对复杂、微小裂纹的检测,研究拟采用改进粒子群算法(IPSO),通过余弦函数、正态分布调节惯性权重,粒子反向学习过程避免了过早收敛,对鸡蛋图像自适应阈值分割后进行增强,以期获得最佳检测视觉结果。
1 改进粒子群算法
1.1 基本粒子群算法
基本粒子群算法中粒子个体l在时刻t+1的第d维空间速度和位置更新公式:

(1)
式中:
c1、c2——加速系数,c1∈[0,4]、c2∈[0,4];
w——惯性权重;
r1、r2——随机数,r1∈[0,1]、r2∈[0,1];


粒子个体在算法运行后期会停滞在局部最优值周围,导致粒子个体不能获得全局最优值,出现数据坍塌现象,无法收敛,因此需改进基本粒子群算法以解决粒子早熟现象的发生。
1.2 改进粒子群算法策略
1.2.1 动态调整惯性权重 粒子群算法中惯性权重w主要功能是调节全局搜索、局部寻优,w值过大不利于后期局部寻优,过小不利于前期全局搜索;w通过线性递减方法也不利于算法的运行,特别是如果检测复杂的鸡蛋裂纹,检测效果较差[8]。因此,需要增加迭代初期的全局搜索范围和减少迭代后期的局部索搜范围,动态调整惯性权重策略:
(2)
式中:
tmax——最大迭代次数;
wmax、wmin——惯性权重最大、最小值;
φ——调整因子,φ∈(0,1);
N(0,1)——正态分布。
w通过第1项、第2项最小惯性权重和余弦函数调节,第3项利用正态分布调整惯性权重整体取值分布,φ主要是控制w的偏离程度,这样使w取值分布更趋于合理,惯性权重动态调整随迭代次数变化如图1所示。
从图1可以看出,在开始时刻w值为0.9,此时增加了粒子的飞翔范围,具有较大的搜索空间;w随迭代次数t增加逐渐减小,最终稳定在0.4,方便了后期的局部寻优。

图1 惯性权重动态调整随迭代次数变化
1.2.2 反向学习 反向学习利用种群初始最差值和个体历史最差值的拉动效应,防止粒子落入极值陷阱,快速找到全局最优位置,在反向学习过程中,调整粒子的飞行速度以便于粒子寻化。

(3)
式中:
μ——均值;
σ2——方差;
γ——扰动因子。
反向学习过程中的粒子速度更新公式:
(4)
式中:
c3、c4——加速因子,c3∈[0,4]、c4∈[0,4];
r3、r4——随机数,r3∈[0,1]、r4∈[0,1];


正常寻优粒子与反向学习粒子对比收敛如图2所示。
从图2可以看出,反向学习粒子通过反向学习比正常寻优粒子更早地获得了最佳收敛值,节省了时间。

图2 正常寻优粒子与反向学习粒子对比收敛
2 鸡蛋裂纹获取
2.1 基于自适应阈值的鸡蛋图像分割
由于鸡蛋形状差异性导致鸡蛋图像不具有相同性,如果采用固定阈值则不能将鸡蛋分割出来,因此根据鸡蛋图像灰度值采用自适应阈值进行鸡蛋图像分割,将预分割图像分为鸡蛋区域和背景区域,鸡蛋区域所占像素点个数与整个图像比值为X0,鸡蛋区域平均灰度值是Y0;背景区域所占像素点个数与整个图像比值为X1,背景区域平均灰度值是Y1,同时整个图像的平均灰度为Y,鸡蛋区域与背景区域的类间方差为Z,则:
(5)
采用遍历的方法使类间方差Z最大,即目标与背景的差异性最大,则此时阈值T即是最佳分割阈值。
2.2 基于改进中值滤波的鸡蛋表面暗斑去除
有些鸡蛋表面存在大小不一的暗斑点,背光照射使点状暗斑、线状暗斑的斑点非常明显,这些暗斑形成的阴影会干扰裂纹检测,因此需去除鸡蛋裂纹周围的暗斑点,同时要尽量减少对裂纹区域的影响。经典中值滤波属于非线性滤波技术,较小的中值滤波窗口能保护鸡蛋裂纹图像的细节信息,但对鸡蛋暗斑点噪声的去除效果不好;较大的中值滤波窗口对暗斑点噪声有较好的过滤效果,但会使鸡蛋裂纹区域变模糊。为了避免中值滤波窗口尺寸难于选择的缺陷,对其改进如下:假设Wij为中心在(i,j)处的滤波窗口,W0为滤波初始窗口大小,Wmax为允许的最大窗口,设fij为(i,j)处的灰度值,fmax为Wij的最大灰度值,fmin为Wij的最小灰度值,favg为Wij的灰度中值。若当窗口Wij非噪点数量≥8时,用窗口中值替代噪点;窗口Wij非噪点的数量<8,则窗口大小增加2,则进行如下步骤:

2.3 鸡蛋裂纹增强
由于获取鸡蛋图像是在背光照射下,因此鸡蛋裂纹部分的明亮度要强于其他部分,裂纹会形成中间亮、两边暗的条状条纹,裂纹部分像素的灰度值明显高于背景像素的灰度值,但是背光照射下鸡蛋表面也会产生亮度不均匀现象,同时鸡蛋表面非常微小裂纹即使在背光透射照明下也不易检出,因此需对其进行增强[9]。试验通过非完全Beta函数F(u)对鸡蛋裂纹进行增强:
(6)
式中:
B(α,β)——Beta函数,α∈(0,10),β∈(0,10)。
对鸡蛋区域图像每个像素进行归一化变换:
(7)
式中:

Lmax、Lmin——分割后鸡蛋区域的最大、最小灰度值。
对归一化鸡蛋区域图像中的每个像素利用非完全Beta函数F(u)进行处理:
(8)
根据鸡蛋区域图像灰度值对区域中的每个像素反变换得到最终增加图像:
(9)
式中:
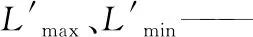
当α、β取得最佳组合值时,鸡蛋裂纹增强效果才最好,因此参数α、β组合问题即可转为粒子算法优化处理。
粒子对鸡蛋裂纹增强的适应度函数设为:
F=(H+S+D)/3,
(10)
式中:
H——熵值;
S——边缘内容;
D——灰度标准方差。
2.4 算法流程
(1) 粒子群初始化,随机产生粒子个体。
(2) 计算粒子的适应度值。
(3) 输入待检测鸡蛋裂纹图像。
(4) 按照式(4)进行更新粒子,若更新后适应度值大于原来个体最优值,则将该粒子位置作为个体最优值,若更新后粒子适应度值大于原来全局最优值,则将该粒子位置作为全局最优值。
(5) 判断是否达到迭代停止条件,连续5次迭代的全局最优值相同或达到最大迭代次数,则进行步骤(6),否则进行步骤(4)。
(6) 输出检测结果。
3 试验仿真
试验仿真中计算机配置为Intel Core i5-9400,集成显卡,内存8 GB,Matlab2007实现编程,粒子群总数为300,迭代最大次数设置为600,c1=c2=c3=c4=2。
3.1 视觉效果分析
从图3、4可以看出,试验算法对鸡蛋网状裂纹、线形裂纹图像均能检测出裂纹,并且裂纹边缘清晰,一定程度增强了鸡蛋的裂纹信息,抑制了斑点噪声,视觉效果较好,其他算法检测鸡蛋裂纹出现断纹以及错误检测,不能将鸡蛋裂纹信息提取出来,同时对复杂的网状裂纹检测错误较多,非明显的线形裂纹则断纹较多。

图3 不同算法对鸡蛋网状裂纹检测的视觉效果

图4 不同算法对鸡蛋线形裂纹检测的视觉效果
3.2 不同裂纹正确检测率分析
从图5可以看出,明显的线形裂纹、网状裂纹检测正确率要高于非明显的线形裂纹、网状裂纹,这是因为裂纹越复杂,裂纹的交叉点越多,越不容易检测,但是试验算法IPSO的不同裂纹正确检测率均高于其他算法,相比AS、NN、ITF、WMM、PSO、GA、MC检测明显的线形裂纹分别高出0.93%,3.31%,5.60%,6.17%,7.37%,8.82%,11.63%;检测明显的网状裂纹分别高出0.74%,3.07%,5.06%,6.13%,7.19%,8.80%,11.01%;检测非明显的线形裂纹分别高出1.87%,2.14%,4.53%,4.67%,6.85%,8.80%,10.17%;检测非明显的网状裂纹分别高出1.23%,1.79%,3.37%,4.54%,6.50%,8.07%,10.12%。

图5 不同裂纹正确检测率
4 结论
针对鸡蛋裂纹图像检测问题,通过余弦函数、反向学习优化粒子群,将鸡蛋图像分割后进行增强,以消除微小
裂纹在背光透射照明下不易检出的缺陷。结果表明,试验算法对鸡蛋网状裂纹、线形裂纹图像均能检测出裂纹,并且裂纹边缘清晰,明显的线形裂纹、网状裂纹正确检测率分别为96.4%,94.7%,非明显的线形裂纹、网状裂纹正确检测率分别为89.2%,87.5%,高于其他算法。试验只针对常见的鸡蛋裂纹进行识别,后续将对复杂、多变、无规则的鸡蛋裂纹图像进行识别。

