《射雕英雄传》中的数学问题

文若璇 吴骏 茶绍好

《射雕英雄传》是武侠宗师金庸的奠基之作。小说以宁宗庆元五年至成吉思汗逝世这段历史为背景，反映了南宋抵抗金国与蒙古两大强敌的斗争。故事讲述了傻小子郭靖背负着家恨国仇闯入江湖，在聪明伶俐的黄蓉帮助下，一路上通过了无数的艰难历程，最终成为“心系天下，为国为民”的一代大侠。这部武侠小说呈现了排列组合、幻方、开方术、四元术、中国剩余定理、乘法口诀等数学问题，通过对这些数学问题的分析，可以进一步加强对文学作品的理解。

一、排列组合

《射雕英雄传》第十二回中，黄蓉设计了一道叫“玉笛谁家听落梅”的菜肴。黄蓉在酒杯里斟了酒，放在洪七公前面，笑道：“七公，您尝尝我的手艺儿怎样？”洪七公哪里还等她说第二句，也不饮酒，抓起筷子便夹了两条牛肉条，送入口中，只觉满嘴鲜美，绝非寻常牛肉，每咀嚼一下，便有一次不同滋味，或膏腴嫩滑，或甘脆爽口，诸味纷呈，变幻多端，直如武学高手招式之层出不穷，人所莫测。洪七公惊喜交集，细看之下，原来每条牛肉都是由四条小肉条拼成。洪七公猜出有5种肉品，但是未猜出有几种变化。黄蓉微笑道：“倘若次序的变化不计，那么只有二十五变，合五五梅花之数，又因肉条形如笛子，因此这道菜有个名目，叫作‘玉笛谁家听落梅。这‘谁家两字，也有考人一考的意思。”

“五五梅花数”涉及数学中的排列组合问题。这里的次序变化不计，只需考虑组合。如果每次咀嚼1种肉，就吃不出变化的味道，至少要咀嚼2种肉才行，而且每根牛肉都是由4条小肉条拼成。那么，可以吃到的不同味道种数为：

C+C+C=25。

在小说中，黄蓉为了让郭靖得到洪七公的武功真传，通过一道美食的吃法，变化多种做法，把一道菜做出25种不同的味道，蕴含着基本的排列组合问题。

二、幻方

在《射雕英雄传》中第二十九回说到黄蓉和郭靖为了躲避铁掌帮来到黑泥潭之地，在那里他们遇见了神算子瑛姑。瑛姑给黄蓉出了一道数学题：“将一至九这九个数字排成三列，不论纵横斜角，每三字相加都是十五，如何排法？”

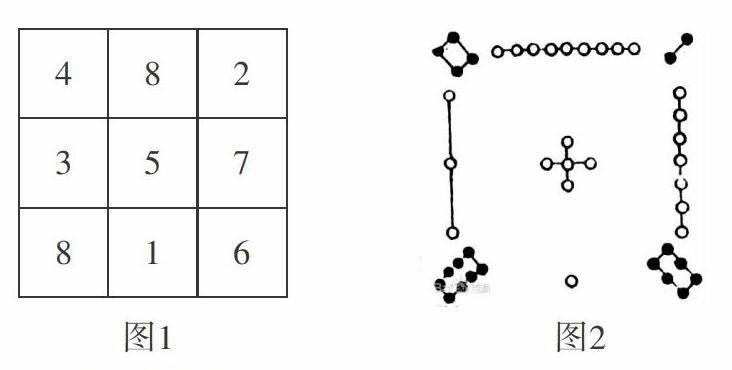
好一个黄蓉，不假思索，当下低声诵道：“九宫之义，法以灵龟，二四为肩，六八为足，左三右七，戴九履一，五居中央。”边说边画，在沙上画了个九宫之图。（如图1所示）

瑛姑以为九宫图是自己的独创秘法，原来早有歌诀传世。其实上图所列“九宫图”，来源于“洛书”。（如图2所示）第一个系统研究幻方的人是我国南宋杰出的数学家杨辉，他總结的解答方法是：九子斜排，上下对易，左右相更，四维挺出。也就是说，先把1～9九个数依次斜排，再把上1下9两数对调，左7右3两数对调，最后把四面的2、4、6、8向外面挺出，这样就得到一个三阶幻方。杨辉研究出三阶幻方后，又系统地研究了四阶幻方至十阶幻方。

在《射雕英雄传》中黄蓉笑道：“不但九宫，即使四四图，五五图，以至百子图，亦不为奇。就说四四图罢，十六字依次四行排列，先以四角对换，一换十六，四换十三，后以内四角对换，六换十一，七换十。这般横直上下斜角相加，皆是三十四。”瑛姑依法而画之，丝毫没有差错。

黄蓉通过自己的聪颖智慧破解了黑泥潭的九宫图迷宫。小说中描述的四宫格、五宫格以至百子图等，说明古人已经掌握了高阶幻方的构成规律。

三、开方术

在《射雕英雄传》第二十九回，黄蓉和郭靖在瑛姑的黑泥潭之地，见地下都是长约四寸、阔约二分的竹片，这正是计数时用的算筹。再看那些算子排成商、实、法、借算四行，暗点算子数目，知她正在计算五万五千二百二十五的平方根，这时“商”位已计算到二百三十，但见到那老妇拨弄算子，正待算那第三位数字。黄蓉脱口道：“五！二百三十五！”

这个题正是《九章算术》少广章中的第十二题：

今有积五万五千二百二十五，问为方几何？答曰：二百三十五步。

译文：假设有面积55225平方步。问：变成正方形，边长是多少？答：235步。

《九章算术》记载了历史上最早使用的开方术，其算法就是把算筹排成“商、实、法、借算”四行进行运算：“商”位置求得平方根数;“实”位置是被开方数;“法”位置为当前所算出的开方数;“借算”位算筹的作用是相当于被开方数的分位点，每隔两位记一分位点。其计算法则与现在笔算方法是一致的。

“算筹”是我国古代人们计算的工具，用竹或木、骨制成的条状物。算筹加之十进制计数法，是为我国传统数学长于计算的重要原因。《老子》说“善数不用筹策”，说明最迟在春秋时期人们已经普遍使用算筹了。

四、四元术

第二十九回中瑛姑对黄蓉的数学才能又惊又疑，带着黄蓉进入内室。只见墙壁围成圆形，地下铺满细沙，沙上画着许多横直符号和圆圈，又写着些“太”“天元”“地元”“人元”“物元”等字。金庸笔下的黄蓉见地下的这些符号时，就知是术数中的难题，那是算经中的“天元之术”。黄蓉从腰间抽出竹棒，倚在郭靖身上，随想随在沙上书写，片刻之间，将沙上所列的七八题尽数解开。

黄蓉微微一笑，道：“天元四元之术，何足道哉？算经中共有一十九元，‘人之上是仙、明、霄、汉、垒、层、高、上、天，‘人之下是地、下、低、减、落、逝、泉、暗、鬼。算到第十九元，方才有点不易罢啦！”

其中，“元”表示未知数，古今意义相同。“天、地、人、物”四元依次代表现当代数学中“X、Y、Z、W”四个未知数，在我国古代算经中已经早有记载。古代的横直符号代表数字，数上加一斜横表示负号，圆圈代表零。“天元术”是宋元时期发展起来的设未知数列方程的方法，特指解只包含一个未知数（天元）的方程，解由“天、地、人、物”四个未知数构成的四元高次方程组称为“四元术”。对于解四元高次方程组，常规的思路就是逐步消元，得到一元高次方程，解出此方程，代回原方程组解出各元。

至于黄蓉所说的“十九元”其实并非代表不同的十九个未知数，而是代表同一未知数的不同次幂，人为常数项，人之上九字表示未知数的各正数次幂（最高为九次），即X、X、X、X、X、X、X、X、X。人之下九字表示未知数的各负数次幂（最低为九次），X、X、X、X、X、X、X、X、X。由这“十九元”构成的方程实质就是一元高次方程。

五、中国剩余定理

第二十九回中，黄蓉也用竹棒在地下细沙上写了三道算题。其中第三题是“物不知其数”问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”这对于神算子瑛姑来说，也是够为难的了。这个问题也称为“中国剩余定理”“鬼谷算法”“韩信点兵”，宋代学者秦九韶对这类题目有很深的研究。

《孙子算经》给出了这类问题的解法：

先从5和7、3和7、3和5的公倍数中相应地找出分别被3、5、7除均余1的最小数70、21、15，即：70÷3=23……1，

21÷5=4……1，15÷7=2……1。之后，用找到的这三个最小数分别乘以被3、5、7除所剩之数，把它们相加起来，即70×2+21×3+15×2=233，再用相加得到的数233减去3、5、7数的最小公倍数的整数倍，即为所求之数：X=233-105n，当n等于2时，得此题的最小整数解为23。此题的通解可以写为：X=23+105n（n∈N）。

明朝数学家程大位在《算法统宗》中将这种解法编成一首通俗的歌谣：“三人同行七十稀，五树梅花廿一枝，七子团圆正半月，除百零五便得知。”这个歌诀给出了模数为3、5、7时的同余方程解法，意思是将除以3得到的余数乘以70，将除以5得到的余数乘以21，将除以7得到的余数乘以15，全部加起来后减去105（或者105的倍数），即得到所求之数。

下面用集合的方法来解答“物不知数”问题，并验证前述解答23的正确性。

除以3余2的数，是3的倍数加上2的数的集合：

A=﹛5，8，11，14，17，20，23，26，…﹜

除以5余3的数，是5的倍数加上3的数的集合：

B=﹛8，13，18，23，28，33，38…﹜

除以7余2的数，是7的倍数加上2的数的集合：

C=﹛9，16，23，30，37，44，……﹜

而全部符合上面三個条件的最小数是23。

六、乘法口诀

第三十回中，郭靖、黄蓉顺着山路走来到一条宽约尺许的石梁处，石梁的尽头是一个极长的缺口，缺口处被一个书生占据了要冲，无法通过。那书生摇头晃脑，正自诵读《论语》，郭靖求见其尊师，但他却似乎全然没有听见。黄蓉出言相激：“孔子弟子七十二人中，有老有少，可知其中冠者几人，少年几人？”书生称《论语》中未曾说起，其他经传中亦无记载。黄蓉引据《论语》“冠者五六人，童子六七人”，由此，五六得三十，成年的是三十人，六七四十二，少年是四十二人。两者相加，不多不少正是“七十二弟子”。那书生折服于黄蓉的聪明才智，佩服她的满腹诗书，于是，带着郭靖和黄蓉去见其师傅。

“九九”的起源很早，韩婴（汉代燕人）《韩诗外传》记载这样一个故事：

齐桓公庭燎以待士，期年而士不至。于是东野有以九九见者，桓公戏之曰：九九足以见乎？鄙人曰：九九薄能耳，而君犹礼之，况贤于九九者乎？桓公曰：善。乃因礼之。期月，四方之士相导而至矣。

这说明在公元前7世纪，懂得乘法口诀已不是什么稀罕的事情了。九九歌诀的一些句子，在诸子百家的文献中也多次出现。依黄蓉的聪慧，背诵乘法口诀是轻而易举的。

《射雕英雄传》中呈现的数学问题，表明了作者具有深厚的数学功底。通过对这些数学问题的解决，刻画了聪明机灵、才智过人的黄蓉形象。读者在自己感兴趣的文学作品里遇见数学，感受到文学与数学的美妙融合。