基于移频外差的高速光电子器件自校准高频分析

张尚剑，王梦珂，张雅丽，张旨遥，刘 永

电子科技大学电子薄膜与集成器件国家重点实验室，成都610054

高速电光调制器和光电探测器是光纤通信系统和无线通信系统中的核心器件. 无线通信技术结合了光和无线通信的优势，包括宽光纤带宽、低光纤损耗、低复杂度和低成本等，广泛应用于卫星通信、移动无线电通信、宽带接入、移动宽带系统和无线局域网等领域[1-2]. 在这些宽带微波应用中，电光调制器和光电探测器的高频响应特性对于精确的电-光信号转换和光-电信号转换至关重要[3].

目前，光调制器频率响应的测量方法主要有光谱分析法[4-7]、扫频法[8-10]、光学下变频法[11]. 光电探测器（photodetector, PD）频率响应的测量方法主要有脉冲激励法[12-13]、强度噪声法[14-15]、扫频法[8-9]、谐波分析法[16-18]、光外差法[19-22]. 光谱分析（optical spectrum analysis, OSA）法利用光谱分析仪分析光调制信号的光谱，最初用于测量马赫-曾德尔调制器（Mach-Zehnder modulator, MZM）和相位调制器（phase modulator, PM）的半波电压. 该方法能够直接在光域内实现MZM 和PM 的高频测试，但因为光栅光谱仪在1 550 nm 波长附近只有2.5 GHz（0.02 nm）的分辨率，所以很难在低频频段（GHz以下）工作. 使用布里渊光谱仪或者外差光谱仪可以提高分辨率，但其分辨率仍然受到光源线宽的影响. 基于光学方法测量PD 高频特性具有无需任何微波器件的优点. 例如，强度噪声法利用放大的自发辐射拍频噪声为光电探测器产生了超宽带的光激励源，但是该方法的频率稳定度和信噪比都比较低[22]；光外差法利用一个或者两个可调谐激光器的波长拍频来实现光电探测器的频率响应测量，但是该方法需要精细地校准线宽的展宽和功率波动的影响[21].

为了实现高分辨率的测量，开始采用电域测试法，其中应用最为广泛的方法是扫频法. 该方法利用矢量网络分析仪或者光波元件分析仪测量MZM 和PD 的相对频率响应[9]，在测量MZM 时需要一个宽带且已校准的PD，而测量PD 又需要一个宽带且已校准的MZM. 因为该方法的测量结果包含了待测器件和辅助器件的级联频率响应，所以针对辅助的PD 或者MZM需要额外复杂的去嵌（de-embedding）操作. 为此，有研究者提出了改进的扫频法，假设以同一个电吸收调制器作为调制器和探测器时的频率响应是一致的，那么使用一个电吸收调制器就可以简化校准的过程，然而这个假设需要特定的条件才能成立[10]. 扫频法最大的困难在于：如果要测量待测器件的绝对频率响应，就必须已知辅助器件的绝对频率响应. 众所周知，绝对频率响应比相对频率响应更全面，它不仅反映了调制效率的相对变化，而且反映了调制效率本身. 更重要的是，相对频率响应很容易从绝对频率响应中得到，反之则不然，可见研究一种可以获得高速光电子器件绝对频率响应的高分辨率、自校准的方法是非常重要的.

最近，我们提出了一种电域测试学方法，以移频和双音调制的方式分别测量了PM 和PD的频率响应，用频率近似相等的双音调制消除了辅助器件引入的频率响应波动[23-25]. 在此基础上，本文利用自外差干涉仪提出了外差映射测试方法体系，可以实现高速光电子器件频率响应的自校准测量. 外差干涉仪包括激光器、马赫-曾德尔调制器、相位调制器、声光移频器和光电探测器. 利用这个外差干涉仪就能把所需光载波和边带从光域映射到电域，并在电域里等效地观察光谱线.采用同一测量系统可以同时测量MZM、PM 和PD 的绝对频率响应，也能得到MZM 的啁啾参数. 本文详细描述了相关理论并通过实验测量了MZM 的调制指数、半波电压和啁啾参数、PM 的调制指数和半波电压以及PD 的响应度，以验证所提方法的正确性.

1 基本原理

图1 为所提出的自校准频率响应测量方法的原理图，其中自外差干涉仪包括激光器、马赫-曾德尔调制器、相位调制器、声光移频器和光电探测器. 自外差干涉仪的上分支为待测MZM（DUT1），其中频率为f1的正弦微波信号υ1(t) =V1sin(2πf1t)加载在待测MZM 的射频电极上；下分支为一个声光移频器级联待测PM（DUT2），其中频率为f2的正弦微波信号υ2(t) =V2sin(2πf2t)加载在待测PM的射频电极上. 干涉仪输出的合路光信号输入到待测PD（DUT3）转换为电信号，并在电谱仪中进行分析.

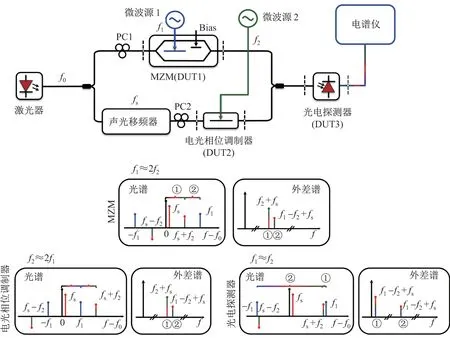
图1 本文所提出的自校准频率响应测量方法的原理图Figure 1 Schematic diagram of proposed self-calibrated frequency response measurement method

在干涉仪的上分支，待测MZM 输出的光信号可以表示为

式中，fc为激光器输出的光载波频率，mzi（i= 1,2）为待测MZM 上臂或者下臂对应的调制指数，ϕ为MZM 的偏置相位. 非对称因子γ为MZM 两臂的分光比，与消光比（extinction ration, ER）有关，两者的关系可以表示为ER=20×lg[(1+γ)/(1−γ)]. MZM 的调制指数和非对称因子可以从传统的光谱分析[5]中得到

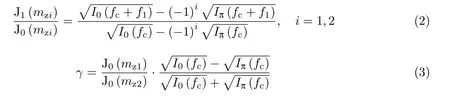
式中，I(f)表示频率为f的光谱功率，下标0 和π 表示偏置相位分别为ϕ=0 或者π 时的情况.

在干涉仪的下分支，待测PM 输出的光信号表示为

但令那些“原教旨主义”保时捷RS家族的拥趸感到遗憾的是，这辆最新的911 GT3 RS居然将空调、音响和导航系统列为了标准配置，甚至还可以选装前桥抬升系统以提高日常的使用便利性。可无论如何，它都是一辆快到令人感到怀疑人生的汽车，所以它也会成为所有喜欢汽车的人所热衷的梦想。

式中，fs为移频器的频率. PM 的调制指数mp也可以从光谱分析[4]中得到

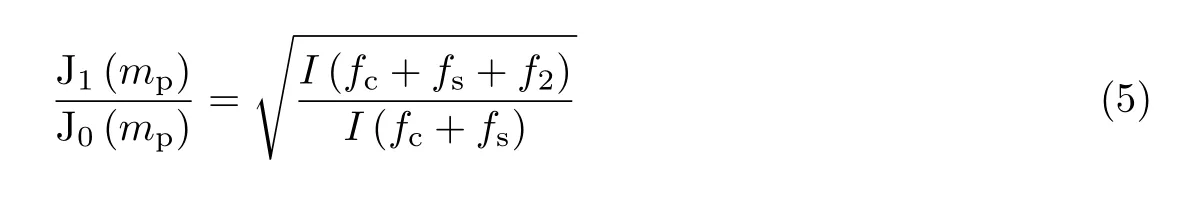
强度调制和相位调制的光信号在干涉仪末端合路之后输入PD 产生瞬时光电流，根据贝塞尔函数展开式可以得到

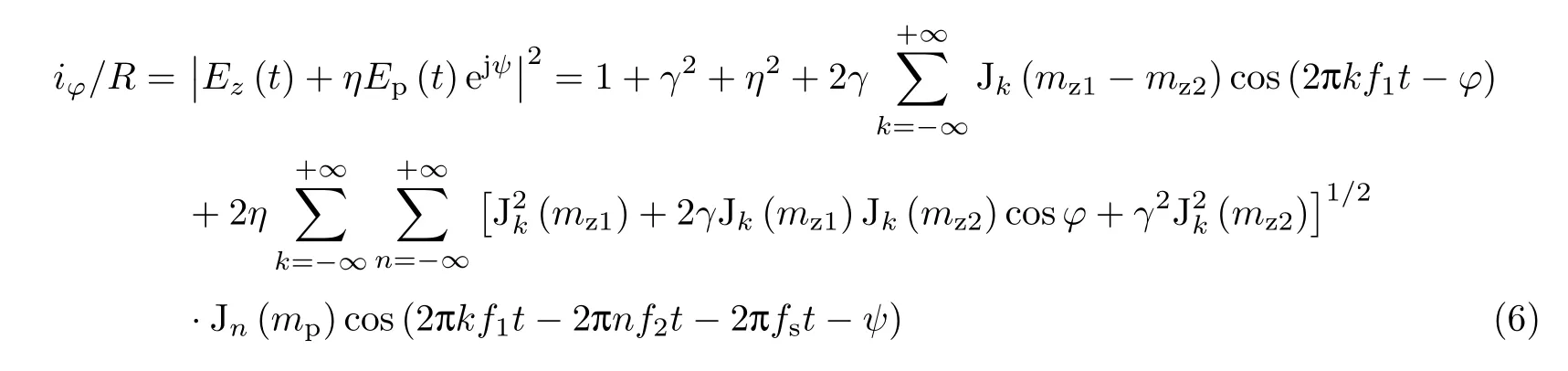
式中，R为PD 的响应度，η（0≤η≤1）和ψ表示干涉仪两分支的相对幅度和相对相位.Jk(·)和Jn(·)分别表示k阶和n阶的第1 类贝塞尔函数（k,n=0,±1,±2,···）. 根据式（6）可以分析出频率为kf1±nf2±fs的拍频边带的幅值如下：

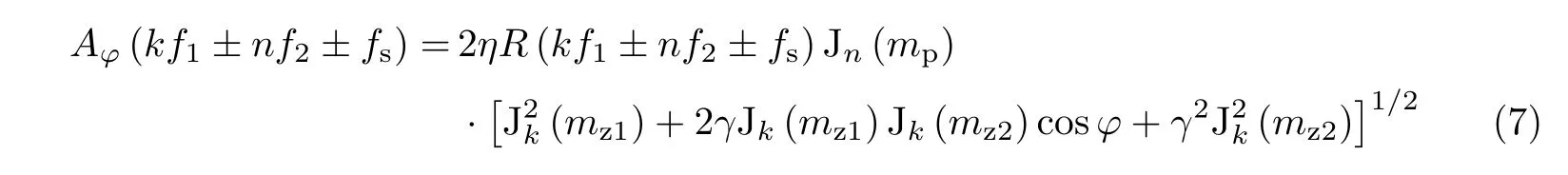
对于待测MZM（DUT1）半波电压和啁啾参数的测量，配置加载在MZM 上的微波频率f1和加载在PM 上的微波频率f2的关系为f1≈2f2≫fs，则近似认为R(f1−f2±fs)≈R(f2±fs)，同时调节待测MZM 的偏置电压使得ϕ= 0或π，根据式（7）可以得到MZM的调制指数和非对称因子分别为

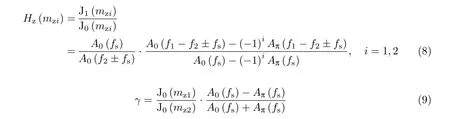
则MZM 的半波电压和固有啁啾参数如下：

对于待测PM（DUT2）半波电压的测量，配置加载在MZM 上的微波频率f1和加载在PM 上的微波频率f2的关系为f2≈2f1≫fs，则近似认为R(f2−f1±fs)≈R(f1±fs)，根据式（7）可以得到待测PM 的调制指数和半波电压分别为

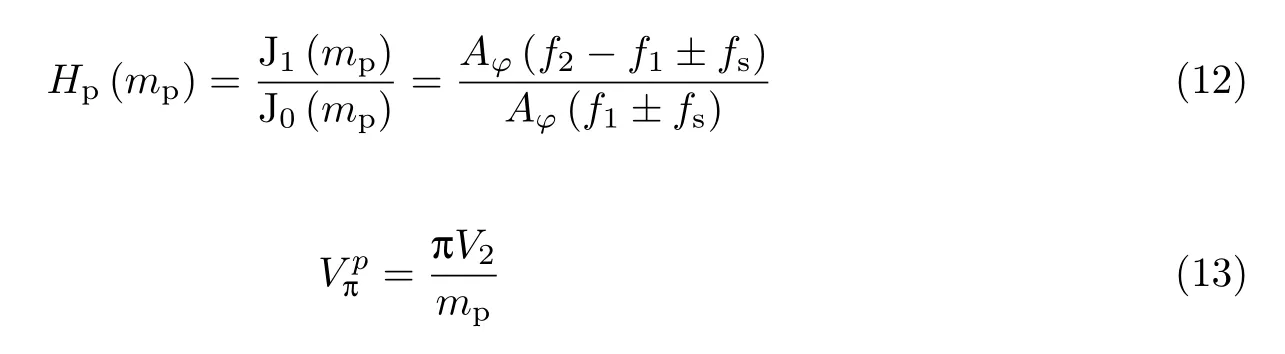
关于待测PD（DUT3）响应度的测量，可以研究频率分量f1±f2±fs，这些频率分量是光强度调制和相位调制边带的和频与差频. 分析式（7）可知，每一对光边带在光域内是均衡的，而在电域内其幅度差异仅取决于PD 的频率响应，于是我们配置加载在MZM 上的微波频率f1和加载在PM上的微波频率f2的关系为f1≈f2≫fs，使得频率分量f1−f2±fs为低频成分，并且频率是固定的，接近直流. 利用式（7）可以得到待测PD 在频率f1+f2±fs相对于固定低频f1−f2±fs的响应度为

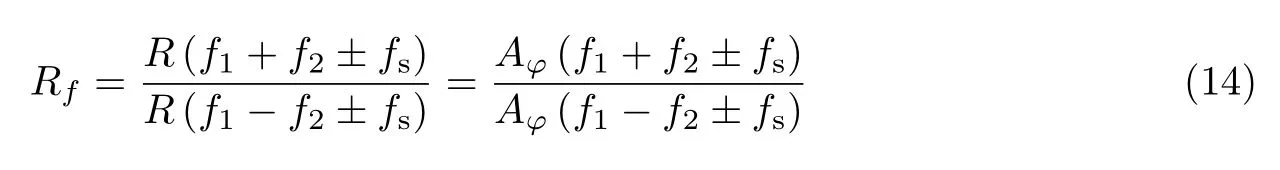
分析式（14）可以看出，根据两个频率分量的幅度之比可以将辅助器件MZM 和PM 的频率响应抵消掉，进而在电域内实现光电探测器频率响应的自校准测量. 特别地，所需外差信号的频率为f1+f2±fs，是f1或者f2的两倍，即实现了两倍的测量频率范围，同时根据以上分析可以得到本文方法的测量频率范围主要受限于电谱仪的工作频谱范围.

结合式（6）和式（8）～（14）可以看出，本文方法只要利用自外差干涉仪就可以实现待测MZM、PM 和PD 频率响应的独立测量，而除了待测器件以外其他辅助器件的频率响应影响则可以通过配置两个微波驱动信号之间的频率关系完全抵消. 测量MZM 和PM 时，在f1或者f2处的频率响应可以根据频率成分f1/2 或者f2/2 得到；测量PD 时，在f1+f2处的频率响应可以根据两个频率成分f1和f2得到，证明了本文方法对于辅助器件只需一半的带宽，相当于实现了两倍的测量频率范围. 值得注意的是，该测量不依赖自外差干涉仪两分支的相对幅度η和相对相位ψ，因为MZM 的非对称因子γ和相位偏置ϕ对于所需频率分量的幅度具有相同的影响效果，所以并不影响最后的测量结果. 值得一提的是，两个微波信号的相位不影响所需频率分量的幅度，因此在测量过程中没有必要保持两个微波信号同步，进一步简化了测量过程.

2 实验

实验中，采用半导体激光器作为光源，输出1 550.12 nm 的光载波. 光功率和线宽分别为5.01 mW 和10 kHz，输入到干涉仪的上下两个分支. 在上分支，光载波被待测LiNbO3MZM调制；在下分支，光载波经过移频频率为fs= 70 MHz 的声光移频器（CETC YSG70）之后，输入到待测PM 中进行电光调制. 其中，待测MZM 和PM 分别由两台微波源（R&S SMB 100 A；HP86320A）输出的微波信号驱动. 干涉仪的两个分支合路之后，光信号经待测PD检测转换为电信号并在电谱仪（R&S, FSU50）中进行分析. 为了实现自动扫频测量，通过NI-VISA数据总线控制微波源和电谱仪，并用一个Matlab 程序去设置两个微波源的频率和功率，再从电谱仪中获取数据进行处理. 为了获得更高的效率，在干涉仪的两个分支分别使用了两个偏振控制器便于两个分支之间的偏振对准，并且在干涉仪的上分支或者下分支分出一部分光调制信号输入到光谱仪（YOKOGAWA AQ6370C）中进行监测，以对比正确性.

测量MZM（DUT1）半波电压和啁啾参数时，配置两个微波驱动信号的频率关系为f1= 2f2+0.02，其单位为GHz. 同时，调节待测MZM 的偏置电压使得所需偏置相位ϕ= 0或π. 由式（7）可知：当ϕ=0时，A在频率fs处的值为最大值；当ϕ=π 时，A在频率fs处的值为最小值. 在偏置相位ϕ为0 和π 这2 种情况下，典型外差电谱分别如图2（a）和2（b）所示. 当f1= 16 GHz、f2= 7.99 GHz、fs= 70 MHz、偏置相位ϕ= 0 时，所需频率分量70 MHz 处的电功率为–14.91 dBm，如图2（a）中的第1 列所示. 在所需频率分量f2−fs=7.92 GHz、f1−f2−fs= 7.94 GHz 这2 种情况下，对应的电功率分别为–26.67 dBm 和–57.93 dBm，如图2（a）中的第2 列所示. 同理，当偏置相位ϕ=π 时，在所需频率分量fs=70 MHz、f2−fs=7.92 GHz、f1−f2−fs=7.94 GHz 这3 种情况下，对应的电功率分别为–27.89 dBm、–39.66 dBm、–49.72 dBm，如图2（b）所示. 因此，根据式（8）和（9）可以计算出待测MZM 的调制指数和非对称因子分别为mz1=0.147、mz2=−0.121、γ=0.631，再根据式（10）和（11）就可以计算出待测MZM 在频率f1=16.00 GHz 处的固有啁啾参数和半波电压分别为0.584 和8.91 V. 实验中，可以根据已获得的非对称因子γ计算得到待测MZM 的消光比为12.91 dB. 值得注意的是，待测MZM 在频率f1=16.00 GHz 处的频率响应是通过分析7.92 GHz 和7.94 GHz（约为8.00 GHz）这2 处的频率分量计算得到的，从实验上证明了辅助器件PM 和PD 只需一半带宽的结论. 在不同调制频率下，所测量到的待测MZM 的调制指数、半波电压和啁啾参数分别图3（a）和3（b）所示. 从图3（b）中可以看到，啁啾参数和半波电压整体上是随着频率的增加而增大的，但是会有一些细节的波动. 根据式（10）和（11）可知，这些波动本质上是与MZM 两臂的调制指数的相对变化有关的，因此半波电压和啁啾参数在某些频率范围内呈现先减小后增大的趋势，也体现了待测MZM 器件本身在射频上的不对称性.

图2 MZM 为待测器件时所需频率分量处测量的外差电谱Figure 2 Measured heterodyne spectra emphasized on desired frequency components in the case of MZM under test

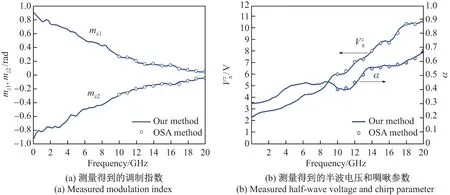
图3 MZM 为待测器件时用本文方法和光谱分析法测量得到的不同调制频率下的调制指数、半波电压和啁啾参数Figure 3 Measured modulation index, half-wave voltage and chirp parameter under different modulation frequencies with our method and with OSA method in the case of MZM under test

测量PM（DUT2）半波电压时，配置两个微波驱动信号的频率关系为f2= 2f1+0.02，其单位为GHz. 图4（a）显示了所需频率分量f1−fs和f2−f1−fs这2 处的外差电谱. 例如，当f1= 5.99 GHz 和f2= 12.00 GHz 时，在所需频率分量f1−fs= 5.92 GHz 处的功率比在f2−f1−fs=5.94 GHz 处的功率小14.77 dB，于是根据式（12）和（13）可以计算得到待测PM在调制频率为f2= 12.00 GHz 处的调制指数和半波电压分别为0.359 rad 和7.80 V.最后，对不同调制频率下待测PM的调制指数和半波电压进行测量，所得结果如图4（b）所示.

测量待测PD（DUT3）响应度时，配置两个微波驱动信号的频率关系为f1=f2+0.1，其单位为GHz. 图5（a）显示了在所需频率分量f1±f2−fs处的外差电谱，图5（b）显示了使用本文方法测得的PD 频率响应，并将其与强度噪声法得到的数据和器件出厂数据进行了对比. 例如，当f1= 6.00 GHz 和f2= 5.90 GHz 时，在所需频率分量f1+f2−fs=11.83 GHz 处的电功率比在f1−f2−fs= 30 MHz处的电功率低5.02 dB，因此根据式（14）可知，待测PD 在频率11.83 GHz 处相对于30 MHz 处的响应度为–5.02 dB. 简单地改变两个微波源的频率就可以得到其他频率处的相对响应度，最后得到了待测PD 在20 GHz 范围内的频率响应，如图5（b）所示.

测量MZM 和PM 时，同时用传统的光谱分析法在相同的驱动功率下对同一个MZM 和PM 分别进行测量，测量结果如图3（a）、3（b）、4（b）所示，并与本文方法进行对比. 对于传统的光谱分析法，从实验数据可以看出测量MZM 和PM 时，测量的最低频率分别为10 GHz 和4 GHz，主要受限于所用光栅光谱仪的分辨率. 因为根据瑞利判据，只有当两个相近波长的幅度相等时，光栅光谱仪才能取得最好的波长分辨率0.01 nm. 这些数据之间的一致性验证了本文方法是可以将光域等效地映射到电域，并且因为光谱分析法不包含任何辅助器件，也就同时验证了本文方法的自校准效果——能够消除辅助器件频率响应波动引入的影响.测量PD 时，将本文方法测量的结果分别与强度噪声法测量以及器件出厂数据进行对比，如图5（b）所示. 这些测量结果之间的一致性也验证了本文方法可以实现PD 频率响应的自校准测量.

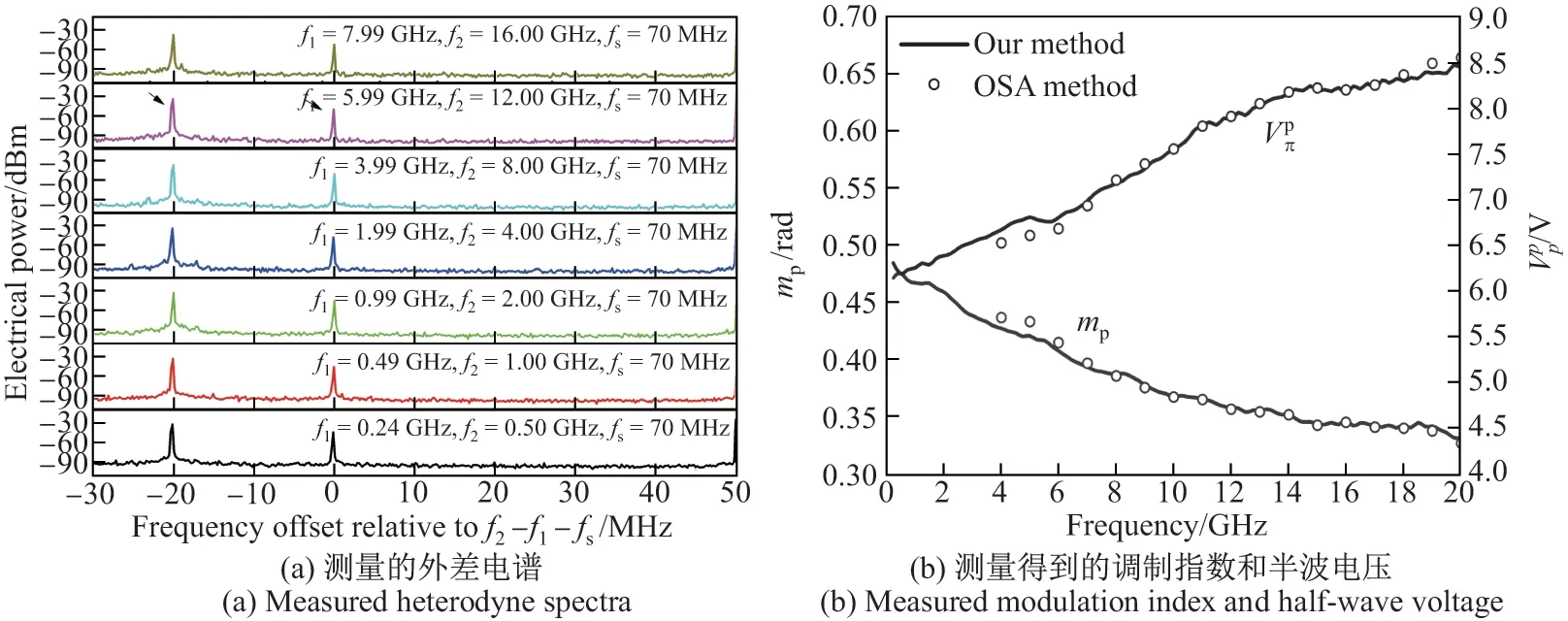
图4 PM 为待测器件时所需频率分量处测量的外差电谱和用本文方法及光谱分析法测量得到的不同调制频率下的调制指数和半波电压Figure 4 Measured heterodyne spectra emphasized on the desired frequency components,and measured modulation index and half-wave voltage under different modulation frequencies with our method and with OSA method, in the case of PM under test

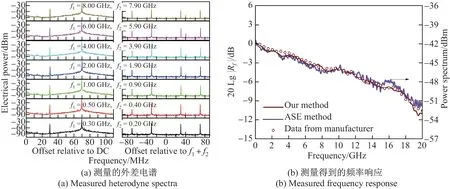
图5 PD 为待测器件时所需频率分量处测量的外差电谱和测量得到的频率响应Figure 5 Measured heterodyne spectra emphasized on the desired frequency components and measured frequency response in the case of PD under test

3 结语

外差谱映射本质上是一种光学微波混频，在无线通信系统和其他微波系统中有许多的应用，比如微波上变频或者下变频. 本文在光学混频中添加了移频，从而实现了从光谱到电谱的完整映射，以测量高速光电子器件的频率响应.

在本文实验中，因自外差干涉仪中两个分支的光信号来自同一个光载波而具有相干性，因此所有的外差信号都显示出非常窄的谱线. 我们的测量对于干涉仪的幅度不均衡和相位差异不敏感，这是因为干涉仪是工作在外差模式而不是干涉模式. 只要两个微波驱动信号满足所需的频率关系，本文方案就可用于不同的驱动功率和工作波长. 另外，除非测量MZM 本身，否则其他器件的测量不需要专门优化MZM 的偏置相位，因为偏置相位对所需的频率分量有相同的影响，所以对最后的测量结果没有影响. 但在实际情况下为了得到更高的外差信号幅度和信噪比，建议调节偏置相位使得cosϕ更大，同时加载合适且均衡的微波驱动功率.

本文方法适用于测量MZM、PM 和PD 的绝对频率响应. 测量MZM 和PM 时，从约为f/2 的频率分量得到待测器件在f的频率响应；测量PD 时，从频率约为f/2 的两个微波驱动信号得到待测器件在f的频率响应. 因此，本文方法减少了辅助器件一半的带宽需求或者把测量频率范围扩展为原来的两倍. 与测量MZM、PM 的传统光学方法相比，本文方法对所需光谱实现了非常高的频率分辨率测量，同时避免了由自外差特性引入的激光器的线宽影响.与测量PD 的传统光学方法相比，本文方法提供了线宽超窄、频率极其稳定且自校准的光激励源. 不同于扫频法，本文方法基于外差谱映射，只用一个共享的外差干涉仪就同时实现了MZM、PM、PD 绝对频率响应的自校准测量. 本文方法最主要的限制来源于测量系统中所需外差电信号的信噪比，因此为了提高准确性，建议在实际测量之前了解辅助器件的带宽. 例如，如果测量MZM，测量频率范围为20 GHz，则最宜选择带宽超过10 GHz 的辅助器件PM和PD.

总而言之，本文提出并验证了一种基于外差谱映射的电学方法. 该方法利用自外差干涉仪对MZM、PM、PD 进行自校准的高频表征；分析光外差信号的高分辨率电谱并提取了包括MZM 的半波电压和啁啾参数、PM 的半波电压和PD 的响应度在内的频率响应；同时消除了系统中其他辅助器件频率响应波动引入的影响，有望用于光电子器件和光子集成电路的在线测量[26-27].