多共振分量融合CNN的行星齿轮箱故障诊断*

汤宝平， 熊学嫣， 赵明航， 谭 骞

(重庆大学机械传动国家重点实验室 重庆，400044)

引 言

近年来，行星齿轮箱被广泛运用在大型复杂旋转机械设备中，如风电机组、直升机等。其内部结构复杂，传动比大，常安装在狭小的空间内，工作环境恶劣且长期处于低速重载的工况下。信号传递路径、其他振动信号和噪声使得行星齿轮箱中某些部件发生故障，特别是早期故障时，故障信息在振动信号中难以被发现[1-2]。

卷积神经网络(convolutional neural network，简称CNN)作为一种典型的端对端的深度学习模型[3]，能够直接以原始振动信号作为输入，自适应地训练卷积核作为滤波器以提取微弱故障特征，无需手工提取和选择特征，降低了对专业人员信号处理知识和实际经验的要求。CNN已在旋转机械故障诊断领域得到了一些应用。Ince等[4]将电流信号作为一维CNN的输入，直接应用于电机的实时故障识别。Zhao等[5]提出了一种基于动态加权小波系数的CNN方法，在行星齿轮箱的故障诊断上取得了良好的效果。Xia等[6]在CNN中进行多传感器的信号融合，以提高故障诊断效果。然而，行星齿轮箱中各级齿轮和轴承的振动成分以及背景噪声相互混叠，传统的基于CNN的故障诊断方法只能通过训练不同的卷积核来辨别与故障相关的振动成分。这一过程不可避免地受到其他振动成分的干扰，造成隐含层中故障相关特征和其他特征难以区分，因此需要结合相应的信号处理方法以增强CNN从混叠信号中提取微弱故障特征的能力。

共振稀疏分解(resonance-based signal sparse decomposition，简称RSSD)[7]是一种非线性信号分解方法。与一般的信号分解方法[8-9]不同，RSSD基于齿轮和轴承故障信号振荡属性的不同，将信号视为高共振分量和低共振分量的合集，利用与信号特征结构最佳匹配的参数化波形表示实际振动信号，从而可以将混叠的振动信号分解为包含齿轮谐波成分的高共振分量和可能包含轴承故障冲击成分的低共振分量，实现齿轮和轴承所激起的振动成分的分离，从而在齿轮箱中各部件的故障诊断中取得了一定效果。黄文涛等[10]提出一种自适应优化品质因子的共振稀疏分解方法，并成功提取出某行星齿轮箱中行星齿轮和行星架轴承的相应特征。李星等[11]在共振稀疏分解的基础上，引入峭度指标，并成功运用在滚动轴承的故障诊断中。

笔者提出了MRCF-CNN的故障诊断方法。首先，采用RSSD将混叠的振动信号分解为高、低共振分量；其次，构建相应的MRCF-CNN模型，从高共振分量中学习齿轮谐波相关的特征，从低共振分量中学习轴承故障相关的特征，并且与从原始振动信号中学习到的特征进行自适应的特征级融合，通过有监督的方式训练模型并进行行星齿轮箱故障诊断。

1 共振稀疏分解

RSSD用两种Q因子不同的小波基函数来稀疏表示一个复杂的信号，利用分裂增广拉格朗日收缩算法(split augmented Lagrangian shrinkage algorithm，简称SALSA)[12]将复杂的信号稀疏分解成高共振分量(振荡次数多的信号)和低共振分量(振荡次数少的信号)，从而实现从相互混叠的振动成分中提取特征信息。

首先，共振稀疏分解面临的问题是如何根据品质因子获得小波函数。品质因子可调小波变换(tunableQ-factor wavelet transform，简称TQWT)[13]通过指定的Q值和冗余度r设计小波，其中所有小波具有相同的品质因子Q。通过图1所示的双通道分解滤波器组实现TQWT，获得高Q和低Q的小波基函数库。

图1 双通道分解滤波器组Fig.1 Double-channel decomposition filter bank

图1中：LPSα和HPSβ分别为低、高通尺度；低、高通尺度参数α和β分别由式(1)确定；H1(ω)和H0(ω)分别为高、低通滤波器频响函数；x为待分析信号；w(1)，w(2)分别为提取出的高Q和低Q小波基函数库。

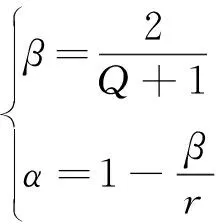
(1)

其中：Q为品质因子；r为冗余度。

将得到的高Q和低Q小波基函数库再通过如图2所示的双通道合成滤波器组，获得高、低共振分量和。J层品质因子可调小波变换如图3所示。

星雨说：“我小时候，每年四月，祖姑婆会用她的小马车带我去洛阳城里小住一段时间，品新茶，看牡丹。姚黄魏紫其实没什么好看，我特别喜欢去洛阳的旅行。由风凌渡过黄河，华山的险峰像一朵朵巨大的莲花开放在远处的原野边上，泾水渭河在更远的地方蜿蜒缓流，嵩山间曲折的山路，路边的松树春天里发出的气味真好闻。在龙门看那些石窟中面目慈悲的佛像，在少林寺山门外看和尚们练拳，一路上霜雪销尽，阳光照着树木发出新芽，翠翠的，路边是不知名的野花，布谷和杜鹃在山林深处啼叫，野猪与鹿被惊吓得乱跑，有时候拉着马车的两匹马都会停下来，吸着山谷里爽利的空气，听成百上千的鸟合唱。”

图3 J层品质因子可调小波变换Fig.3 J-layer tunable Q-factor wavelet transform

TQWT的分解层数受信号长度的限制，信号经过一定层数的分解滤波后，导致信号太短难以被分解。为了避免由于分解层数过多导致结果中参数难以获得的问题，需要控制层数J的大小，使第J层小波的长度不大于待分析信号的长度。根据上述理论，文献[13]给出如下公式

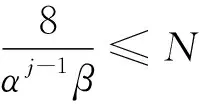
(2)

将式(1)代入式(2)，可得到式(3)

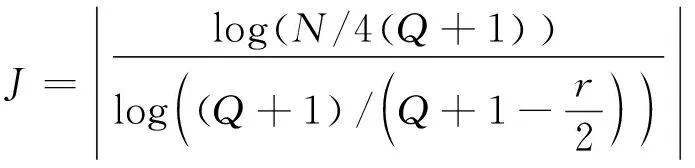
(3)

其中：N为信号长度；|·|为向下取整数。

其次，在信号分解过程中采用如式(3)所示的由形态分量分析(morphological component analysis，简称MCA)[14]建立的目标函数。

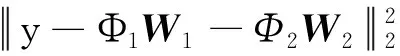
(4)

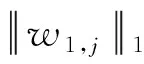
可以看出，式(3)综合考虑了信号分解后残余分量的大小和高、低共振分量的稀疏程度。

2 多共振分量融合卷积神经网络

基于RSSD能有效地从混叠信号中提取所需的特征成分，而CNN在训练卷积核时易受到其他振动成分的干扰，提出一种将RSSD和CNN相结合的多共振分量融合卷积神经网络的方法，实现行星齿轮箱的故障诊断。该方法的流程如图4所示。首先，对输入的振动信号x进行RSSD，得到高共振分量y1和低共振分量y2；其次，将y1，y2和振动信号x分别经卷积层C1，C2和C3运算的结果进行特征融合，输出的结果进行一系列的批规范化(batch normalization，简称BN)、修正线性单元(rectified linear unit，简称ReLU)[15]激活函数以及卷积运算，输出的特征图经全局均值池化后，在输出层中得到分类结果。

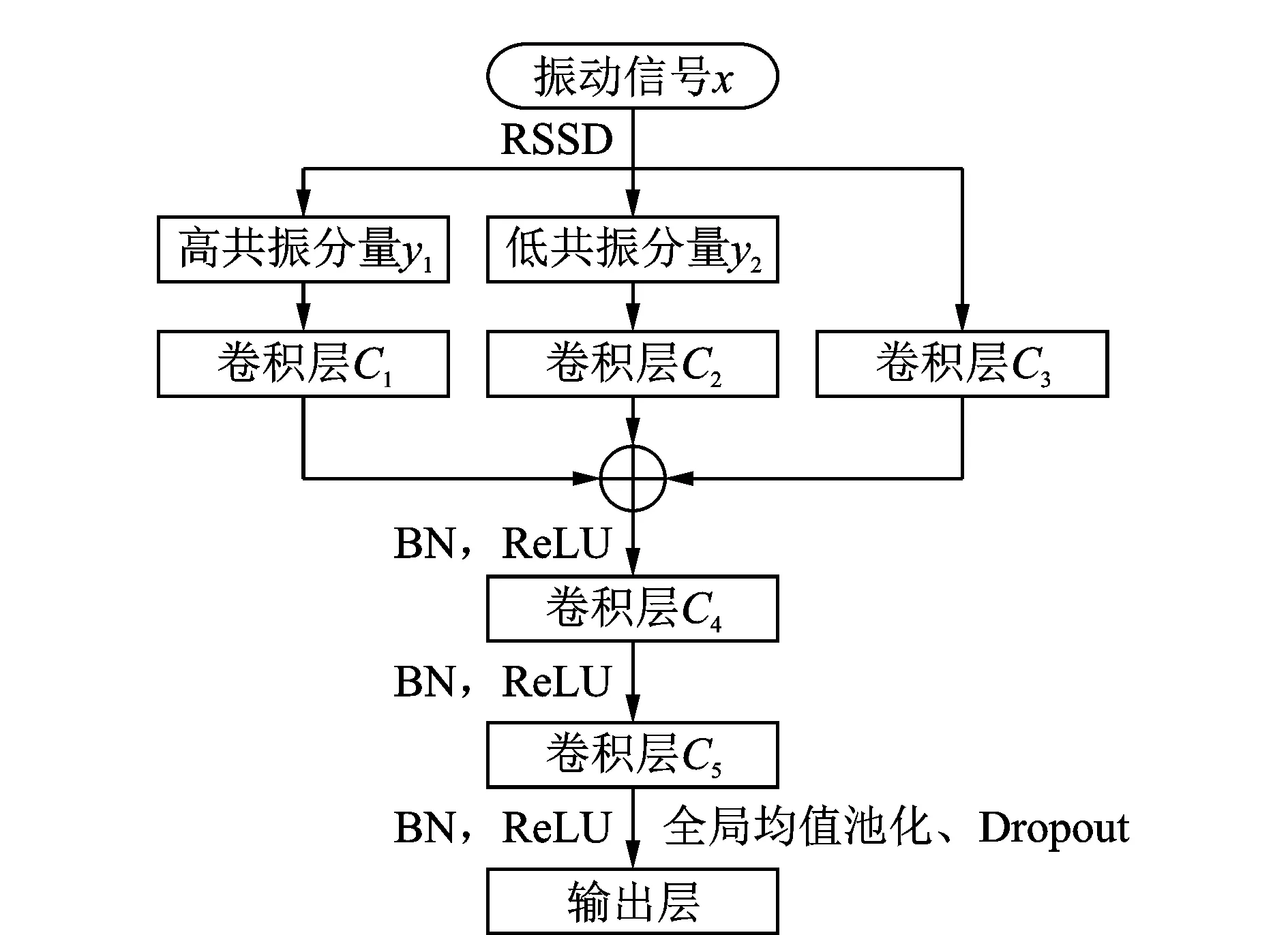
图4 基于MRCF-CNN的故障诊断流程图Fig.4 Flowchart of fault diagnosis based on MRCF-CNN

2.1 卷积层

卷积层将输入信号与卷积核进行卷积运算，并产生相应的特征。卷积层中同一个卷积核以固定的步长遍历一次输入，即权值共享，这一特点可以达到降低卷积层网络参数规模的目的，从而可以减轻由参数过多造成的过拟合，同时可以避免系统所需内存过大。卷积运算公式如下

(5)

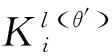
2.2 多共振分量融合

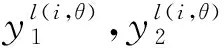
(6)

融合之后的结果y(n)进行BN和ReLU激活函数操作，处理之后的结果作为下一层卷积层的输入。

2.3 全连接输出层

全连接层的主要作用是对前端网络提取出的特征进行分类。经多个卷积层、BN、激活函数以及全局均值池化运算后得到的输出作为全连接层的输入，全连接层中的每个神经元与前1层的所有神经元进行全连接。在全连接层引入Dropout[16]，是为了防止训练时出现过拟合的情况。具体操作是，在训练神经网络时的每次迭代中，以一定的概率舍弃部分神经元，舍弃的神经元的输出都被设置为0，并且停止更新，从而提高网络的泛化能力，防止过拟合的情况发生。

2.4 损失函数

损失函数是用来评价一段输入信号在神经网络的输出与其目标值一致性的函数，选择一个合适的损失函数是十分重要的。卷积神经网络中有几种常用的损失函数，如平方差误差函数以及交叉熵损失函数，适用于不同的问题。本研究采用的损失函数为交叉熵损失函数，可表示为

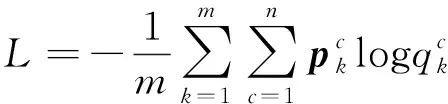
(7)

其中：m为输入的小批量的大小；q为CNN实际输出的Softmax值；样本标签p表示为one-hot类型的向量；n为目标类别个数。

选择交叉熵损失函数是因为针对多分类问题，交叉熵损失函数的训练速度在一般情况下相较于平方差误差函数要快[17]。

3 实验验证及结果

采用TensorFlow 1.0实现了所提出的MRCF-CNN模型，将其应用于行星齿轮箱的故障诊断，采用10折交叉验证进行重复验证，并且进行了严格的实验对比，证明了MRCF-CNN方法的优越性。

3.1 实验数据

采用图5所示的动力传动故障诊断综合实验台(drivetrain diagnostics simulation，简称DDS)进行实验。该实验台主要由电机、两级行星齿轮箱、两级平行齿轮箱和磁粉制动器组成，加速度传感器安装位置如图所示。

图5 动力传动故障诊断综合实验台Fig.5 Drivetrain diagnostics simulation

通过更换行星齿轮箱的滚动轴承和齿轮，模拟了7种不同的行星齿轮箱健康状态，如表1所示。设置采样频率为12 800 Hz，采样长度为200 k，通过调节磁粉制动器的电压(0，4和8 V)获得不同的载荷，电机转频分别设置为20，30和40 Hz，共得到9种不同的工作状态。同时每种健康状态在不同的工作情况下重复进行4次采样，共获得36组数据。其中，每个样本的点数为16 384，经移位共得到65个样本，即每种健康状态的样本数为2 340个，如表2所示，每段信号中均添加了信噪比为5 dB的高斯白噪声以模拟实际工程中存在的噪声干扰。

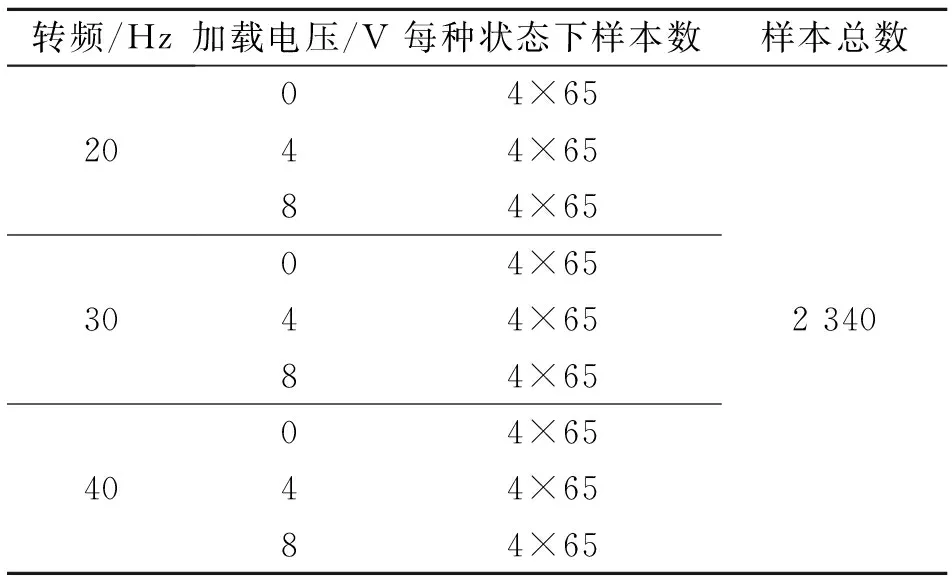
表2 每种健康状态的样本数

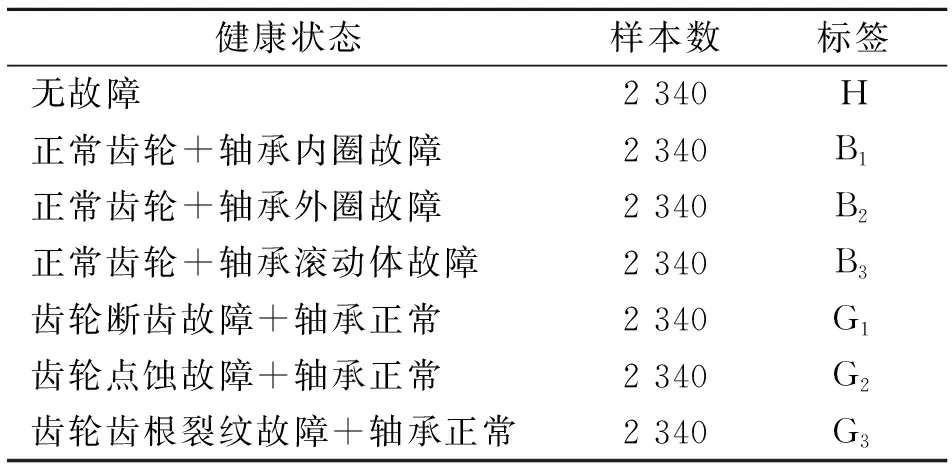
表1 行星齿轮箱的7种健康状态

3.2 超参数设置

MRCF-CNN的超参数设置参照了经验性的建议。其中，初始学习率为0.1，在第20个Epoch降为0.01，在第40个Epoch降为0.001，训练的Epoch代数为50，动量为0.9，小批量为128。MRCF-CNN模型的超参数设置如表3所示，Dropout率为0.5，L2正则化系数设置为0.005。

表3 MRCF-CNN模型的超参数设置

3.3 实验结果分析

为更好地了解MRCF-CNN模型的工作流程，从所有的样本中随机选取一个样本，对其卷积层C1～C3、特征融合后的结果、C4和C5及输出层的特征进行可视化，其结果如图6所示。其中，图6(j)输出层特征表明该样本是最可能被分类到的故障类别，可看出该样本被分类成类别3的概率最大。

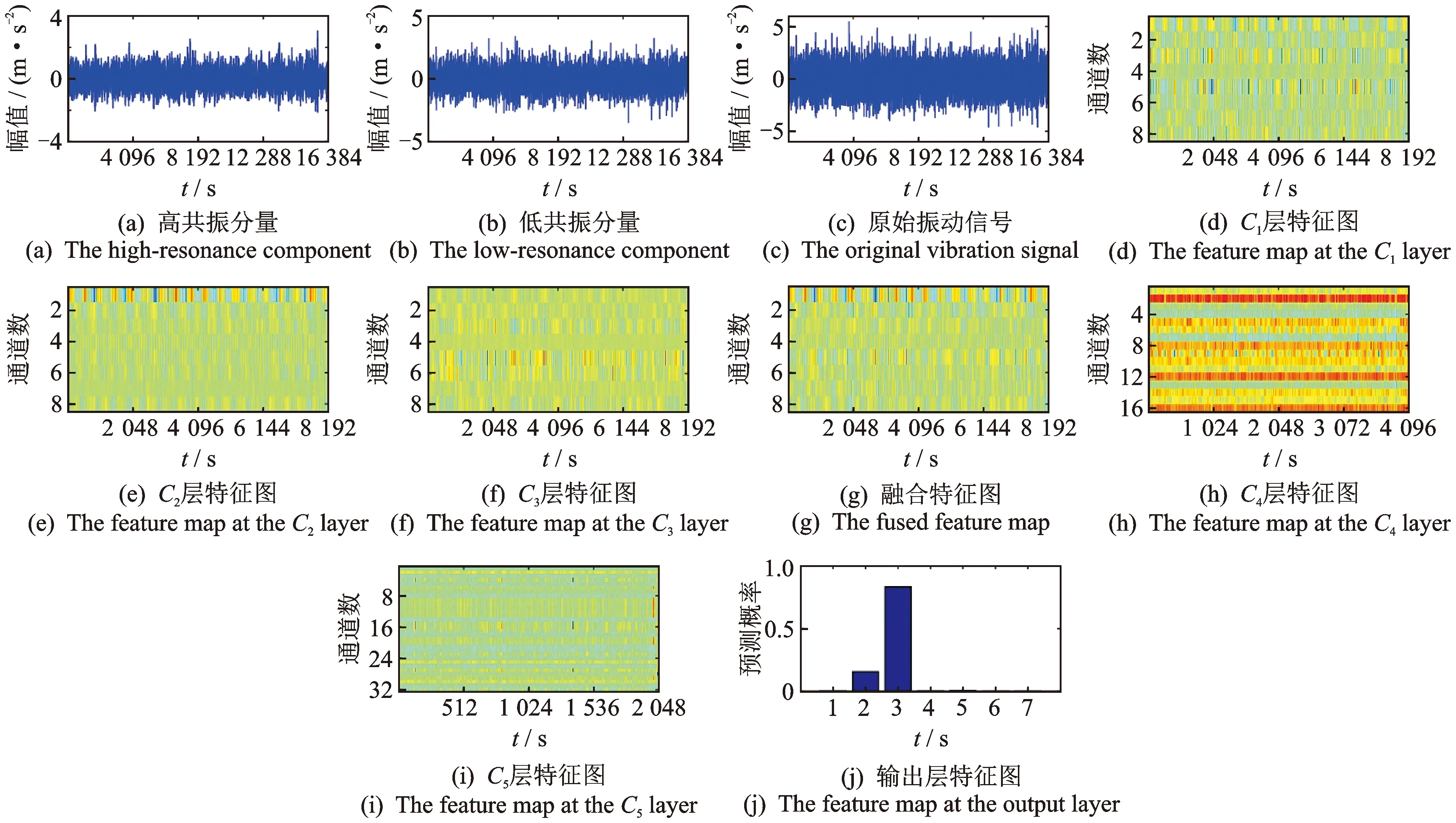
图6 MRCF-CNN模型网络层特征可视化图Fig.6 Feature visualization of MRCF-CNN network

为验证提出方法的有效性，首先将MRCF-CNN模型与传统的浅层机器学习方法进行了对比。从振动信号中提取时域特征并分别作为k最近邻(k-Nearest Neighbor，简称kNN)、支持向量机(support vector machines，简称SVMs)和浅层神经网络 (shallow neuron networks，简称SNN)的输入，所得到的平均测试准确率如表4所示。可以看出，所提出的MRCF-CNN的平均测试准确率相较于kNN，SVMs和SNN分别提高了7.77%，13.23%和16.77%，验证了MRCF-CNN的有效性。

为了验证多共振分量融合的有效性，与未改进的CNN进行了对比，如表4所示，x-CNN，y1-CNN和y2-CNN分别表示以原始振动信号、高共振分量和低共振分量作为CNN的输入。可以看出，MRCF-CNN的平均测试准确率相较于x-CNN，y1-CNN和y2-CNN分别提高了1.74%，5.04%和7.84%，说明所提出的MRCF-CNN能够自适应地调整高、低共振分量和振动信号在故障分类中的作用，更加综合全面地进行故障诊断，具有更强的故障辨识能力。

同时，为了证明MRCF-CNN模型能够从高共振分量中学习齿轮谐波相关的特征，从低共振分量中学习轴承故障相关的特征，对y1-CNN，y2-CNN的轴承故障和齿轮故障的平均测试准确率进行了对比。表4中，针对3种齿轮故障的分类，y1-CNN的平均测试准确率为84.86%，y2-CNN的平均测试准确率为81.34%，y1-CNN的平均测试准确率比y2-CNN的高3.52%，说明高共振分量中所包含的齿轮故障信息多于低共振分量。针对3种轴承故障的分类，y1-CNN的平均测试准确率为83.33%，y2-CNN的平均测试准确率为84.37%，y2-CNN的平均测试准确率比y1-CNN的高1.04%，说明低共振分量中所包含的轴承故障信息多于高共振分量。

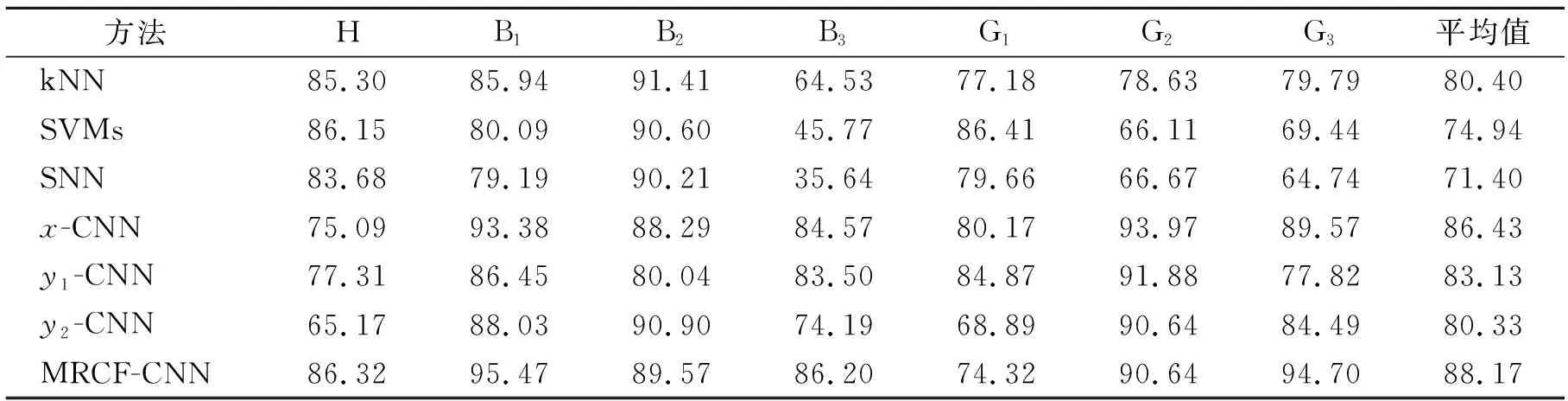
表4 平均测试准确率

4 结束语

笔者提出了一种新的CNN模型，即MRCF-CNN，并成功运用于行星齿轮箱中滚动轴承和齿轮的故障诊断。相较于传统的故障诊断方法，MRCF-CNN不仅降低了对先验知识、信号处理理论和实际经验的要求，而且通过RSSD将原始振动信号分解成包含谐波成分的高共振分量和可能包含轴承故障特征的低共振分量，通过训练卷积层的参数以自适应地调整高、低共振分量和原始振动信号在故障诊断中的贡献，从而提高CNN算法对微弱故障的学习效果。实验结果表明，提出的MRCF-CNN能够提高行星齿轮箱的故障诊断准确率。