基于深度渐进式反投影注意力网络的图像超分辨率重建
胡高鹏,陈子鎏,王晓明,2*,张开放
(1.西华大学计算机与软件工程学院,成都 610039;2.西华大学机器人研究中心,成都 610039)
(*通信作者电子邮箱hgp9411@163.com)
0 引言
在如今数据爆炸的时代,图像数据占据着尤为重要的地位,同时人们对图像分辨率的需求也越来越高。但是依靠提高硬件设施来提高图像的清晰度,不仅难度大、成本高,而且实用性差。图像超分辨率(Super-Resolution,SR)技术便是使用数字信号处理技术将单张LR图像或一组LR图像序列重建成HR 图像。作为近些年来研究的热点问题,图像SR 任务又可分为单帧图像超分辨率(Single Image Super-Resolution,SISR)[1-9]、多帧图像超分辨(Multi-Frame Super Resolution,MFSR)[10-12]和视频超分辨率(Video Super-Resolution,VSR)[13-15]。本文主要研究单帧图像超分辨率的问题,即只利用单幅图像的高频和低频信息进行图像SR重建。
随着对SR 任务研究的深入,涌现出了大量的SR 算法,这些算法大致可分为三类:基于插值的方法、基于重建的方法、基于学习的方法。由于近些年深度学习在计算机视觉各领域都取得了突出的表现,所以基于学习的SR方法也成为了超分辨率技术研究的热点。Dong 等[1]首次将卷积神经网络应用于SISR 问题,提出了(Super-Resolution Convolutional Neural Network,SRCNN),并取得了优越的表现。Kim 等[2]提出了(Super-Resolution using Very Deep Convolutional Network,VDSR),使用残差的思想缓解了梯度消失或梯度爆炸的问题,将网络层数增加至20 层,由于只学习图像的高频信息,所以提高了收敛速度,同时在VDSR中使用了较大的感受野来提升效果并且在单模型中考虑到了多尺度问题。之后Kim 等[3]考虑到参数规模的问题又提出了(Deep Recursive Convolutional Network,DRCN),即使用递归的网络结构,共享网络结构之间的参数,有效地降低了训练的难度;另外作者还采用跳跃连接和集成策略,进一步提高性能。随后Shi等[4]提出 了(Efficient Sub-pixel Convolutional Neural Network,ESPCN),使用LR图像作为输入,在网络结构的后端使用亚像素卷积层隐式地将LR 图像映射为HR 图像,有效地降低了计算复杂度,提高了重建效率。Lai 等[5]提出的LapSRN(deep Laplacian pyramid Networks for fast and accurate Super-Resolution),将拉普拉斯金字塔的思想引入到了深度学习中,实验结果证明了逐级上采样操作的优越性,并且在训练的过程中监督每一水平预测的残差结果,使得性能进一步提升。Lim 等[6]通过去除文献[7]中多余的模块,并且使用L1范数作为损失函数的方式提出了(Enhanced Deep residual networks for single image Super-Resolution,EDSR)网络结构。文献[6]将训练好的低倍上采样的模型作为高倍率上采样模型的预训练,不仅提高了训练的速度,同时训练的结果也更好。
以上这些网络结构多为前馈结构,忽略了HR 图像和LR图像的相互依赖关系和上采样LR 图像时的误差。鉴于此Haris等[8]提出了一种不断迭代地进行上采样和下采样的网络结构。文献[8]使用上下采样相互连接策略和错误反馈机制学习HR 和LR 的相互映射关系,并且使用深度级联的结构级联不同阶段的HR 和LR 特征重建HR 图像;但是忽略了在重构HR 图像时,不同阶段产生的HR 特征的贡献可能不同,并且由于网络的深度增加导致重建的HR 过于平滑,丢失了部分高频信息。针对这些问题,本文提出了深度渐进式反投影注意网络,即使用渐进式上采样至特定的倍数并且引入注意力机制进一步提升了深度反投影网络的性能。本文的主要工作有两个,分别如下:
1)引入了渐进式上采样的思想,对于输入的LR 图像逐步上采样至特定的尺寸,这不仅有效地减少了上采样过程中引入的噪声,还由于每次缩放相对较小的倍率,缓解了上采样过程中信息丢失的问题,同时也降低了网络的计算复杂度。
2)使用注意力机制为渐进式反投影过程中每阶段产生的特征图以及特征图的各个通道,自动分配不同的注意力资源。使网络模型可以学习到尽可能多的高频信息,并尽量减少上下采样过程产生的误差。
1 深度反投影网络超分辨率算法
针对SISR 任务,之前大多数的网络模型都是采用前端上采样、渐进式上采样或后端上采样方法,但这些方法都忽略了重建过程中造成的重构误差。Haris等[8]引入了迭代反投影方法,提出了深度反投影网络(Deep Back-Projection Networks for super-resolution,DBPN)结构,同时引入了密集连接的思想发展DBPN 为D-DBPN(Dense DBPN)。作者主要使用了误差反馈机制、相互连接的上采样和下采样策略以及深度级联等思想构建深度网络结构。D-DBPN 采用迭代反投影的思想,多次模拟图像上采样及下采样的过程,并计算每次上下采样中的误差,利用误差反馈机制指导下次的上下采样过程,以降低重建误差。
投影单元分为上投影单元和下投影单元。对于输入大小为M×N的LR特征图Lt-1上投影单元计算流程被定义为:
上采样:

下采样:

计算误差:

上采样:

输出特征图:

其中:*表示空间卷积算子;↑s和↓s分别是尺度为s的上下采样;pt,gt和qt分别代表在t阶段的卷积或者反卷积核;Ht表示得到的大小为pM×pN的HR特征图。
对于输入大小为pM×pN的HR 特征图Ht下投影单元的计算流程被定义为:
下采样:

上采样:

计算误差:

下采样:

输出特征图:

深度反投影网络虽然已经在SR 任务中取得了卓越的表现,但是仍存在一些问题。它使用相互连接的上下投影单元学习LR 图像和HR 图像之间的相互依赖关系,但是一方面由于使用了较深的网络的结构,造成参数规模较大难以训练;同时在训练过程中丢失了部分的高频信息,使得产生的结果缺少了边缘和纹理等细节信息。此外该网络结构平等地对待每个阶段产生的HR 特征图,忽略了各个特征图之间的相互依赖关系以及各个特征图之间各通道的相互依赖关系。另一方面,虽然D-DBPN 使用相互连接的上下投影单元学习LR 图像和HR 图像之间的相互依赖关系,但是在上采样时仍是直接放大至所需的尺寸。这种方式特别是在高倍率缩放时,会造成部分高频信息丢失和参数规模增加等问题。
2 本文方法
D-DBPN[8]方法对提取到的特征图直接上采样至给定的倍率,但在高倍率时容易丢失高频信息。此外,在重建预测图像时均等地对待各阶段产生的特征,忽略了特征图之间的差异性。本文受到LapSR[5]和RCAN(Residual Channel Attention Networks)[9]的启发,提出了深度渐进式反投影注意力网络。由于使用渐进式上采样策略,所以减少了在上采样过程丢失的高频信息,同时产生的结果具有更丰富的细节信息。此外,引入全局注意力机制对相互连接的不同阶段的特征图以及不同特征图的不同通道分配不同的注意力资源,以学习到更深层次的特征信息。本文提出的深度渐进式反投影注意力网络结构如图1 所示,由浅层特征提取、渐进式反投影、特征注意、重建等四部分组成。

图1 本文算法的网络结构Fig.1 Network structure of the proposed algorithm
2.1 浅层特征提取
首先Ih和Ir分别表示大小为M×N和大小为M'×N'的HR 图像和LR 图像,并且满足M>M'和N>N'。此外,conv(f,n)表示卷积层,其中f代表滤波器的大小,n表示滤波器的数量。对于输入的LR 图像Ir,首先使用conv(3,n0)提取浅层特征L0。然后使用conv(1,nr)将提取到的n0维的浅层特征的维度减少到nr。其中n0代表提取LR图像浅层特征时,需要的滤波器数量,nr表示投影单元需要的滤波器数量。
2.2 渐进式反投影策略
鉴于上采样过程很容易引入噪声,尤其在高倍率采样过程中容易丢失高频信息,为此本文提出了渐进式反投影策略。即对于提取到的浅层特征,使用渐进式反投影单元缩放至所需尺寸,其中每个反投影单元都包含上投影单元和下投影单元。
1)上投影单元。上投影单元结构如图2(a)所示,首先将输入的LR 特征图Lt-1映射到特定的尺寸得到特征图,然后再模拟下采样的过程,尝试将特征图映射到LR 空间得到特征图Lt,这一过程被称之为反投影的过程。但是由于在计算HR 和LR 特征之间映射和反映射时总会存在误差,故计算特征图Lt-1和由上采样得到的特征图Lt之间的误差。然后对进行相同的上采样操作得到,用得到的误差指导到映射过程,最后得到上采样投影的输出HR 特征图Ht。
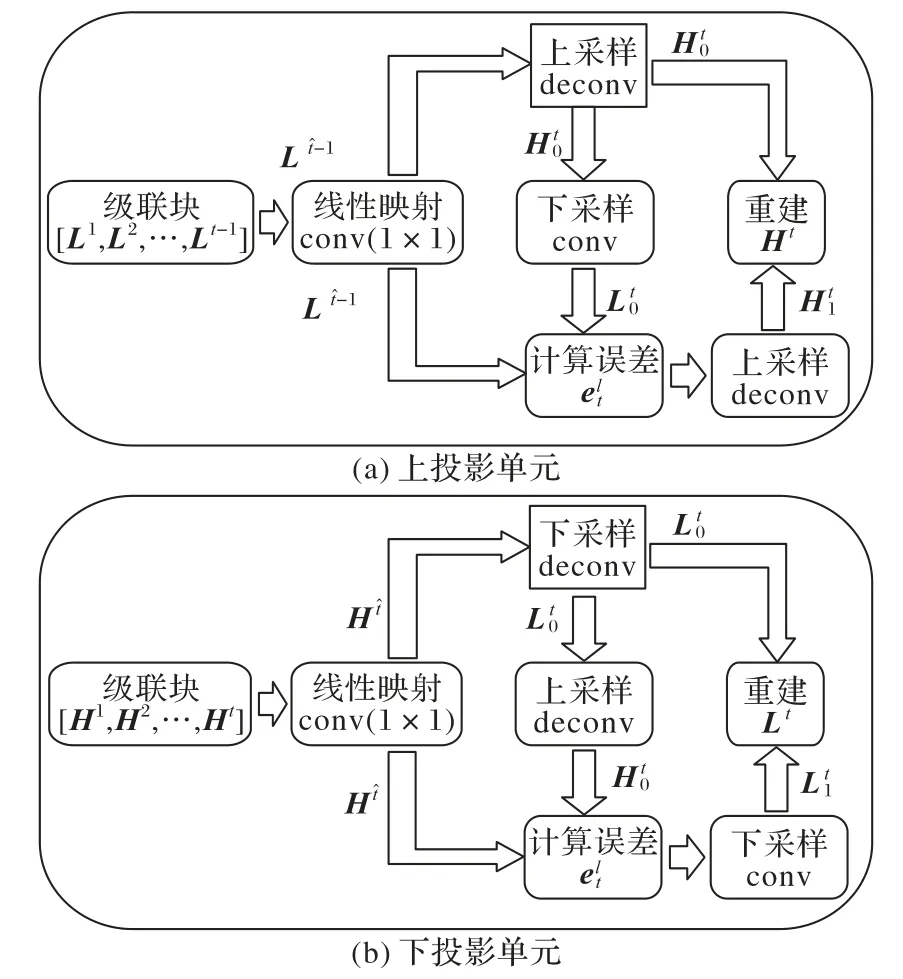
图2 不同单元结构示意图Fig.2 Schematic diagrams of different unit structures
2)下投影单元。下投影单元的结构和上投影单元相似如图2(b)所示。上投影单元的输入是LR特征图Lt-1,而下投影单元的输入则是经过上投影单元产生的HR 特征图Ht。故而首先将输入的特征图Ht映射至LR 空间得到特征图,然后再将特征图映射至HR 特征图并计算特征图Ht和之间的误差。最后将投影误差下采样得到用以指导Ht到的映射过程得到LR特征图Lt。
此外,将需要上采样t倍的任务划分为lb(t)个子任务,每个子任务都包含若干个反投影单元。对于第k子任务,采用密集连接的方式级联之前k-1 个子任务的预测结果。由于采用渐进式的上采样操作,所以每个子任务所产生的HR 特征图尺寸不同。为了解决每个预测特征图尺寸不同的问题,在每个子任务开始之前使用转置卷积的方法将之前各子任务输出的特征图上采样至所需尺寸。此外对于lb(t)个任务中的每个子任务,均使用迭代的反投影单元学习LR 和HR 图像之间的相互依赖关系,渐进式反投影策略有效地缓解了高倍率缩放时的信息丢失和引入噪声等问题。
2.3 全局注意单元
全局注意力单元结构如图3 所示,即将之前所有上投影单元的输出结果[H1,H2,…,Hn]都渐进式地上采样至给定的尺寸并级联在一起得到H×W×C的特征图。对于输入的H×W×C的特征图X=[H1,H2,…,Hn],先进行全局池化操作,逐通道进行分析Z∈RC,Z的第c个元素可以定义为:
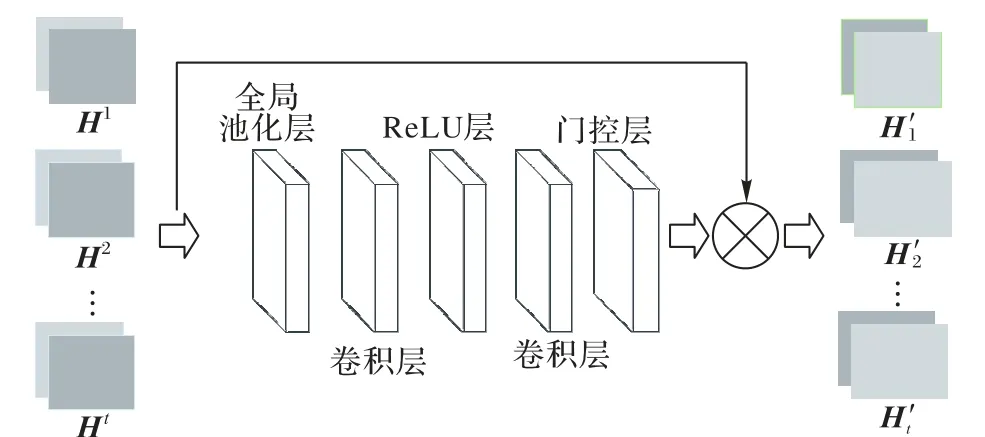
图3 全局注意力机制单元结构示意图Fig.3 Schematic diagram of global attention mechanism unit structure
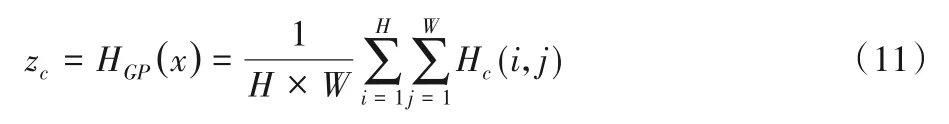
其中:Hc(i,j)代表在第c个特征图(i,j)处的特征值xc;HGP(x)表示全局池化函数。全局池化得到zc描述了第c个通道的特征图的全局信息,同时也将第c通道的特征信息映射为一个数值。之后利用设计的门控函数计算每个通道特征应该分配多少注意力。门控函数被定义:

其中:f(·)和δ(·)分别表示sigmoid 门控单元和ReLU 激活函数;WD是卷积层的权重矩阵,该卷积层将输入的特征图的维度进行下采样,采样比率为r,然后用ReLU 函数激活;WU表示上采样卷积层的权重矩阵,采样比率同样是r,同时该卷积层的激活函数使用sigmoid 函数,从而得到注意力分配比率。最后被分配过注意力的特征图可以通过式(13)计算得到:

其中:sc和Hc分别表示第c通道的特征的注意力分配比率和第c通道的特征图,而H'c表示被分配注意力资源的特征图。
2.4 重建
最后,使用conv(3,3)的卷积层对全局注意力单元得到的特征图进行重建得到大小为M×N的高分辨率预测图像Isr,重建层如式(14)所示:
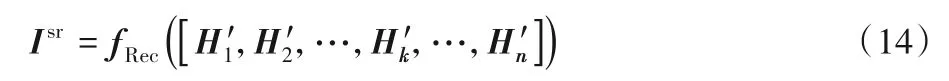
其中:Isr表示预测得到的高分辨率图像;fRec(·)是3 个卷积核大小为3×3的卷积函数;H'k表示分配过注意力的各个阶段的特征图。
针对超分辨率回归任务,通常选择L1范数损失和均方误差(Mean Squared Error,MSE)损失作为网络模型的优化目标,为了选择出更适合本文方法的损失函数,在3.1 节选择不同的损失函数进行对比实验。实验结果表明使用L1范数更适合作为本文方法的优化目标,故本文的实验均选择L1范数损失函数。假设给定的训练集,其包含N个LR输入图像和对应的HR 真实图像,则渐进式反投影注意力网络的优化目标是最小化L1损失函数:
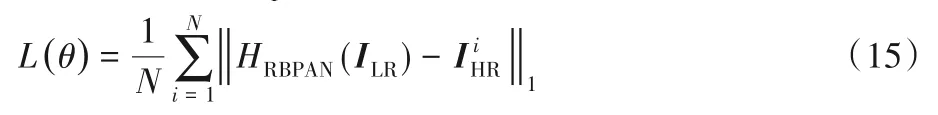
其中:HRBPAN(·)表示本文整体的网络模型预测函数;θ代表本文网络结构中所涉及的参数;L(·)表示本文方法的损失函数。此外本文使用随机梯度下降法最小化L1损失函数。
3 实验与结果分析
由于本文采用渐进式反投影策略,所以在该网络结构中每次采样时都只使用大小为6 ×6 ×64 的卷积核、步长和填充大小都为2 的反卷积层,同时在每个反投影单元中均使用相同的配置。在训练网络模型时使用数据集DIV2K[16],不做数据集增强。此外,使用He 等[17]提出的方法初始化网络权重,并且batchsize 设为20,训练时LR 图像大小为32 ×32。初始的学习率为1E-4 并且每迭代5×105次学习率降低至原来的1/10,一共迭代106次。另外使用动量为0.9 的Adam[18]优化方法,使用L1范数作为损失函数。所有的实验均部署在Nvidia TITAN X(Pascal)GPU 以及Intel Xeon W-2125 CPU 环境下。
3.1 L1范数损失函数和MSE损失函数对比
由于损失函数在网络模型中重要的作用,所以在构建网络模型时损失函数的选择就显得尤为重要。本文选取目前最常见的损失函数即L1范数损失函数和MSE 损失函数,进行实验对比并选择出更适合本文算法的损失函数。
为此,本实验使用缩放因子为4,反投影单元数量为6 的配置构造了模型Ⅰ和模型Ⅱ,模型Ⅰ为使用MSE 损失函数作为网络模型优化目标的,模型Ⅱ为使用L1范数损失函数作为网络模型优化目标的。同时为保证实验的公平性原则模型Ⅰ和模型Ⅱ使用相同大小的卷积核和相同的网络深度,其实验结果表1所示。
从表1中可以发现在Set5 数据集上,使用L1范数作为损失函数的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)指标和结构相似性(Structural SIMilarity,SSIM)指标均高于使用MSE 损失函数的指标,同样在Set14 数据集上有相同的结论,故此认为L1范数损失函数更适合作为本文算法的优化目标。
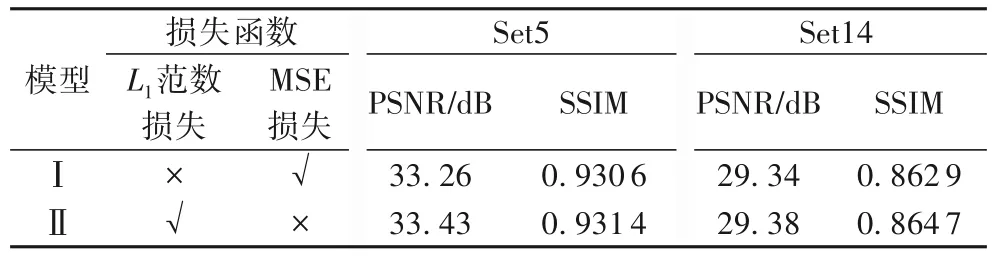
表1 在Set5和Set14数据集上对比不同损失函数的表现Tab.1 Performance comparison of different loss functions on Set5 and Set14 datasets
3.2 模型分析
本文方法不仅引入了注意力机制,而且融入渐进式上采样策略来提升超分辨率的结果。为了验证所提出的网络模型每部分的有效性,构建了三个网络模型,即模型Ⅲ、模型Ⅳ和模型Ⅴ。其中模型Ⅲ是文献[8]中使用6 个反投影单元的DDBPN 模型,模型Ⅳ和模型Ⅴ的设置分别如下:在模型Ⅳ中,只引入了注意力机制。该模型使用和模型Ⅲ相同数量的反投影单元,在缩放因子为4 和8时,分别使用8×8 和12×12 的反卷积核。在模型Ⅴ中,不仅引入了注意力机制,并且融合了渐进式上采样的操作,使用相同数量的反投影单元。但是在缩放因子为4和8时,均使用6×6的反卷积核。实验对比了各网络模型在不同数据集上分别上采样4 倍和8 倍时的PSNR 和SSIM[19]的取值,实验结果如表2所示。
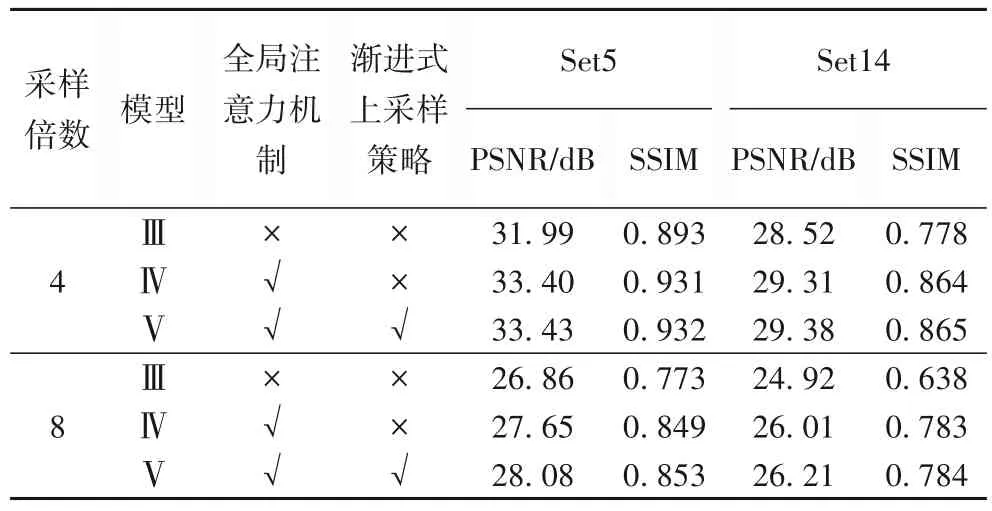
表2 模型Ⅲ、模型Ⅳ和模型Ⅴ在Set5和Set14数据集上的表现Tab.2 Performance of Model Ⅲ,Model Ⅳand Model V on Set5 and Set14 datasets
实验结果表明,在相同数量的反投影单元的情况下,模型Ⅳ和模型Ⅴ在放大4倍和8倍时的重建结果,相较于模型Ⅲ在PSNR 指标和SSIM 指标上都取得了大幅度的提升。其中相对于模型Ⅲ算法在缩放因子为4时,模型Ⅳ和模型Ⅴ:在Set5 数据集上的PSNR 分别提高了1.41 dB 和1.44 dB,SSIM 分别提高了0.038 和0.039;在Set14 数据集上PSNR 分别提高了0.79 dB 和0.86 dB,SSIM 分别高了0.086 和0.0867。当缩放因子为8时,模型Ⅳ和模型Ⅴ相对于模型Ⅲ:在Set5 数据集上PSNR 分别提高了0.79 dB和1.22 dB,SSIM 分别提高了0.076和0.08;在Set14 数据集上PSNR 分别提高了1.09 dB 和1.29 dB,SSIM 分别提高了0.145 和0.146。同时可以观察到模型Ⅴ相对于模型Ⅳ,无论是在Set5数据集上还是在Set14数据集上,缩放因子为4和8时在PSNR指标上和SSIM指标上均有提高。经以上分析可见,本文融合的注意力机制和渐进式上采样思想每部分都展示了其优越性,这都得益于其不同特征图的差异性和小步幅的上采样过程会减少特征信息的丢失,同时可以发现本文算法在缩放因子较大时重建结果取得了更优越的表现。
3.3 参数规模
在本节选取部分主流深度学习的方法与本文算法的参数规模大小进行对比,选取的部分主流算法包括SRCNN[1]、VDSR[2]、LapSRN[5]、EDSR[6]、D-DBPN[8]、RCAN[9]、MemNet[20]、FSRCNN(Faster SRCNN)[21],比较结果如图4所示。
图4(a)展示了当缩放因子为4时,本文所提出的算法和各主流算法在Set5 数据集上测试时的参数规模。从图4(a)中,可以发现当缩放因子为4时,本文所提出的算法比EDSR[6]的参数量减少了66.7%并且重建图像的质量提高了约1 dB。同样当缩放因子为8时,本文算法的参数量虽然有些增加,但是仍维持在一个相对较小的水平(如图4(b)所示)。本文算法预测图像的质量高于EDSR 的预测结果约1.2 dB,相对于EDSR[6]效果参数量减少了66.7%。
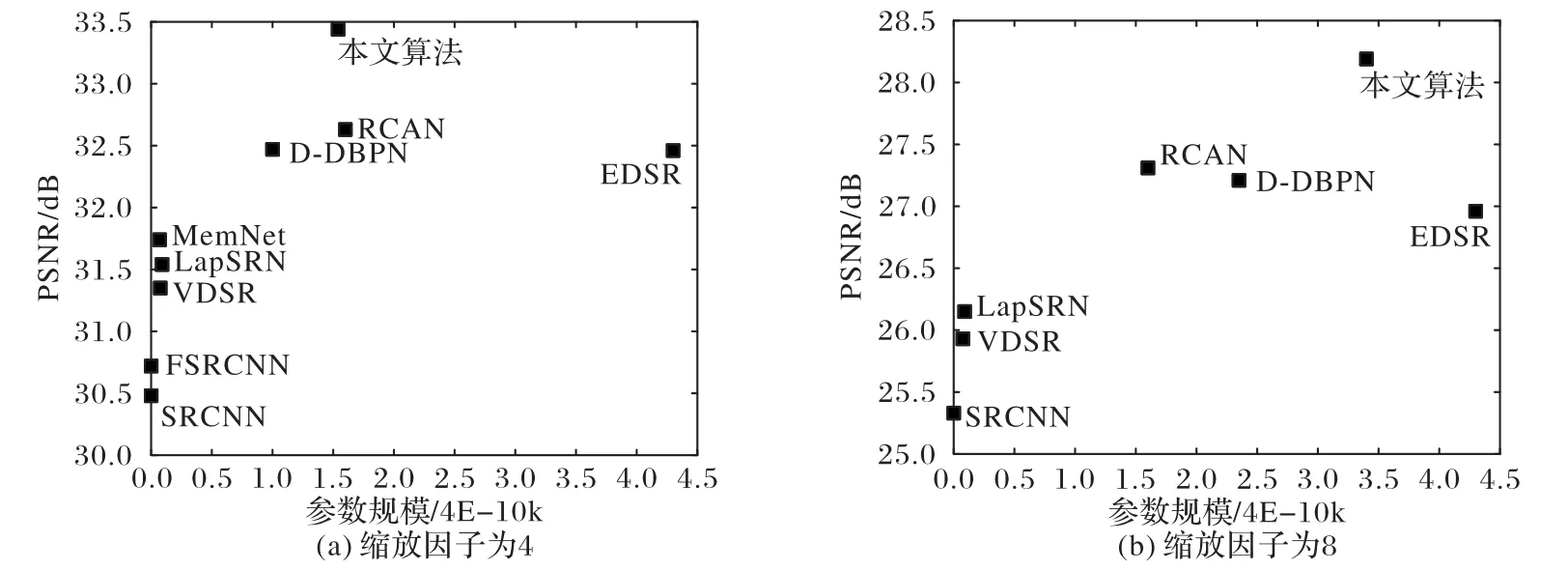
图4 Set5数据集上各主流算法在不同模型的参数规模对比Fig.4 Parameter scale comparison of mainstream algorithms on Set5 dataset
本文采用渐进式上采样的策略,并且使用感受野较小的卷积核,同时网络层数也相对较少,所以网络并没有引入的大量的参数。但是由于算法的优越性,保证了预测图像的质量维持在一个相对较高的水平。
3.4 综合实验结果对比分析
本节将本文方法与部分主流的深度学习算法在不同的数据集上分别上采样不同的倍数取得的实验结果进行对比分析。实验所采用的数据集分别是Set5[22]、Set14[23]、BSDS100[24]以及Urban100[25],其中每个数据集有不同的形态特征,Set5、Set14和BSDS100包含有多个自然场景,Urban100包含具有不同频段细节的城市场景。本文对比的主流深度学习算法包括SRCNN[1]、VDSR[2]、LapSRN[5]、EDSR[6]、D-DBPN[8]、RCAN[9]、MemNet[20]、FSRCNN[21]、SCN (Sparse Coding based Network)[26]、SRMDNF(learning a single convolutional Super-Resolution Network For Multiple Degradations)[27]和RDN(Residual Dense Network for image super-resolution)[28]并且分别计算这些主流算法上采样2 倍、4 倍和8 倍时的PSNR 和SSIM 值并对比分析。为了保证实验的公平性,对以上算法使用了相同的训练集,并且比较在各测试集上的平均结果。缩放因子为2、4和8时的实验结果如表3~5所示。
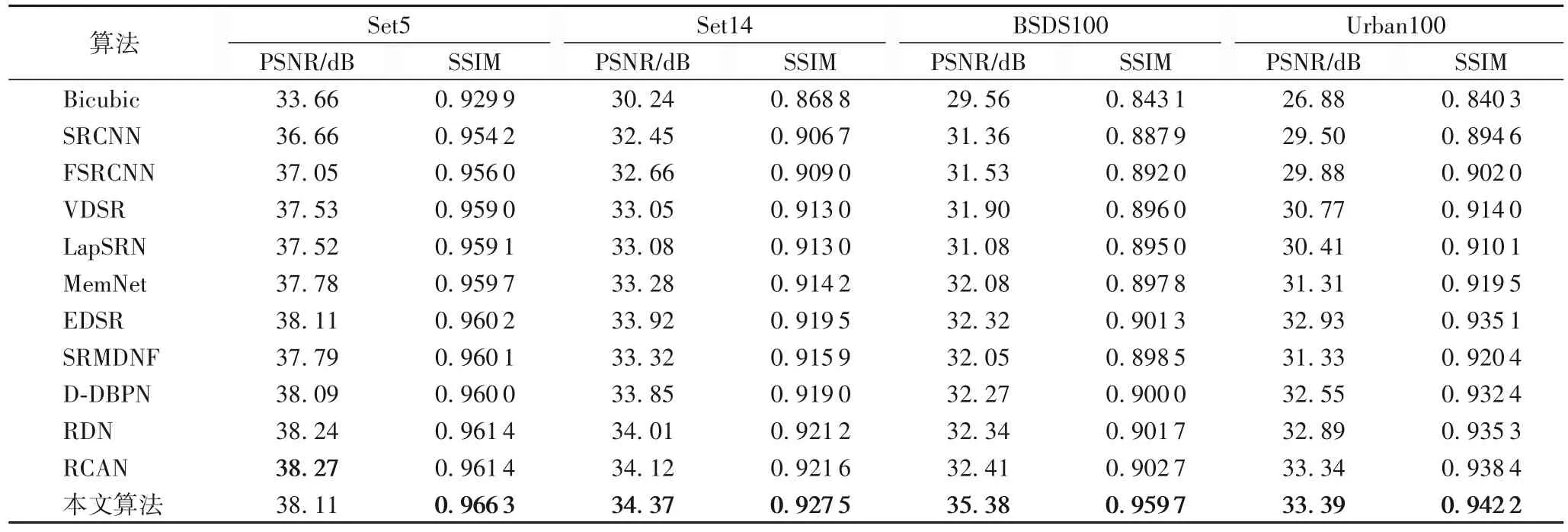
表3 各SISR算法的×2模型在不同数据集上的性能Tab.3 Performance of×2 models of various SISR algorithms on different datasets
从表3~5中可以发现,在缩放因子为4 和8时,本文所提出的算法在各数据集上PSNR 和SSIM 均取得了最好的表现。在缩放因子为2时,本文的算法在Set5数据集上PSNR 并没有取得最优的表现,SSIM 也只有微小的提升,但是在其余数据集上各指标均达到了最优的重建效果。其中在BSD100 数据集上缩放因子为4时与其他算法相比,本文算法的PSNR 提升最明显达到了30.93 dB,相较于次最优算法RCAN的PSNR提高了3.16 dB。同时由于本文更关注缩放因子较大的重建效果,所以总体上缩放因子越大,本文算法的优越性展现得越明显。
图5展示了部分主流算法在scale=4时,对Set5、BSDS100、Set14 和Urban100 数据集中的women、monarch、167083 和img_005 四幅图像的预测结果。观察各算法重建的women 图像的局部放大效果,可以发现Bicubic 等算法预测结果最模糊,其眼睛区域较平滑和模糊,而本文算法在眼睛区域获得了更为丰富的细节信息和较为清晰的边缘。同时比较其他两幅图像,同样发现monarch 放大区域花瓣的边缘更加锐利,167083 和img_005 放大区域的线条也更加明朗。所以本文算法的重建结果无论在客观指标还是在视觉效果上,都展示出了明显的优越性。
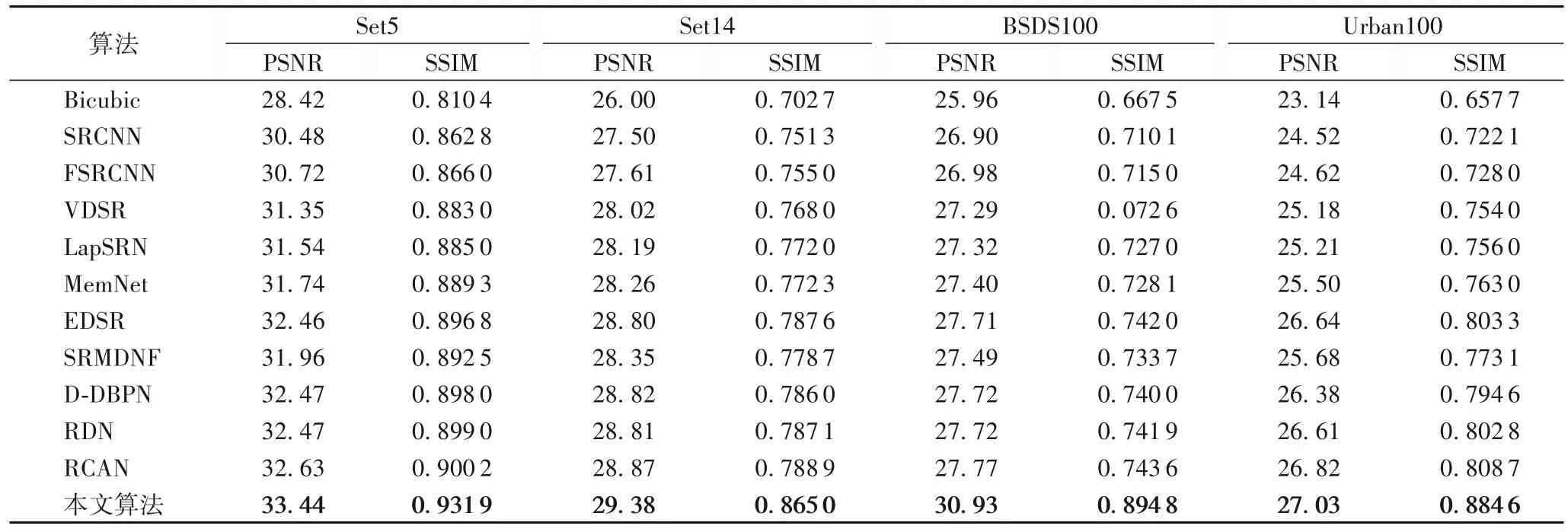
表4 各SISR算法的×4模型在不同数据集上的性能Tab.4 Performance of×4 models of various SISR algorithms on different datasets

表5 各SISR算法的×8模型在不同数据集上的性能Tab.5 Average performance of×8 models of various SISR algorithms on different datasets

图5 几种算法对4幅图片的预测结果对比Fig.5 Prediction results comparison of several algorithms for 4 images
4 结语
本文提出了深度渐进式反投影注意网络,主要利用渐进式上采样的思想并结合了迭代反投影方法和注意力机制,缓解了目前主流算法上采样过程中的高频信息丢失,忽略了高低分辨率图像之间的相互依赖关系以及不同特征通道对重建高分辨率图像的贡献大小不同等问题。本文算法不仅充分发掘了高低分辨率特征图所携带的细节信息,还使用注意力反投影网络学习到了高低分辨率特征图以及特征图各通道之间的相互依赖关系,并且引入渐进式上采样的策略减少了上下采样过程中信息的丢失,同时实验结果表明了本文算法的优越性。

