求解排列组合问题的解空间动态缩减策略

李章洪，梁晓磊，田梦丹，周文峰

（武汉科技大学汽车与交通工程学院，武汉430065）（*通信作者电子邮箱liangxiaolei@wust.edu.cn）

0 引言

排列组合优化问题是一类NP-hard 问题，此类问题规模的扩大将导致解空间呈指数式增长，对求解算法具有极高的要求。典型的问题有旅行商问题（Travel Salesmen Problem，TSP）、车辆路径调度问题（Vehicle Routing Problem，VRP）、船舶配载（Stowage Optimization，SO）问题等。现代智能优化算法是解决排列组合优化问题的主要方法，目前主要集中于对蚁群优化（Ant Colony Optimization，ACO）算法、模拟退火（Simulated Annealing，SA）算法、遗传算法（Genetic Algorithm，GA）、免疫算法（Immune Algorithm，IA）等启发式算法及其改进等方面，其思路主要以算法自身机制调整及多种算法混合进行算法性能提升。例如：针对TSP，为了避免传统遗传算法容易陷入局部最优解的缺点，于莹莹等［1］引入贪婪算法对种群进行初始化；何庆等［2］将模拟退火算法和遗传算法进行了有效的组合；胡云清［3］提出了一种混沌模拟退火算法来求解VRP，提高了问题的求解速度。针对传统蚁群算法求解速度慢、容易陷入局部最优解的问题，周永权等［4］对蚁群算法信息素的更新规则做出了改变；吴新杰等［5］通过改进基本的蛙跳算法，增大了搜索空间，在一定程度上防止了TSP容易早熟的缺陷；王艳等［6］引入对数递减的惯性权重来影响萤火虫的位置，并结合遗传算法中的选择、交叉、变异等概念对萤火虫算法进行改进；为了增强烟花算法求解TSP的稳定性、提高收敛速度，蔡延光等［7］提出了一种混沌烟花算法。上述为此类问题的研究提供了较好的思路和解决方法，但集中于算法自身搜索机制的改进，对算法搜索行为和问题特征的融合分析较少，当问题规模急剧增加时仍然面临着解空间过大、个体有效搜索缓慢、群体搜索停滞等问题。而通过群体搜索过程中解的分析，可知群体迭代搜索中解具有一定的重叠相似性，如可以利用这一特点进行解空间的缩减，将会大幅度降低群体搜索成本，提高搜索效率。本文正是通过对排列组合优化问题解自身特点的研究，提出了一种解空间动态缩减（Solution Space Dynamic Compression，SSDC）的个体编码策略，并将这种新的编码策略应用于TSP和VRP进行求解。

1 具有解空间动态缩减的改进算法构建

1.1 典型排列组合优化问题模型

排列组合是组合学最基本的概念。排列就是指从给定个数的元素中取出指定个数的元素进行排序；组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合优化是指从可能出现的情况中寻找到最优或者近优的解。旅行商问题（TSP）是排列组合问题中的典型问题，不失一般性，本文主要以旅行商问题进行问题分析。TSP 是一类典型的排列组合优化问题，是指商人从起点出发，然后遍历剩下的全部城市，最后回到起点，要求从中找到一条距离最短的路径。TSP的数学模型如下：

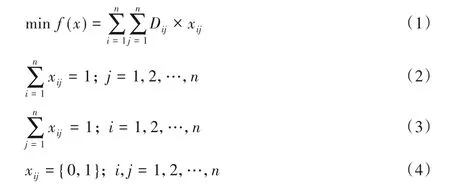
其中：n为城市的个数，Dij为城市i到j的距离，xij为从i到j路径长。

1.2 解空间动态缩减策略

以TSP 为例，通过对排列组合问题求解过程中多个可行解个体表达的分析，比较其结构时会发现，部分排列片段具有重复出现的现象。通过对TSP、VRP 等问题解的图像观察，这些重复出现的排列大概率是特征较优的路段，也就是对求解结果比较有利的路段。冯志雨等［8］通过聚类的方法，将TSP分割成较小的簇来对问题进行求解；饶卫振等［9］提出了距离矩阵方差最小法来对TSP 的距离矩阵进行改进；程毕芸等［10-12］在蚁群算法的基础上提出了一种二次更新信息素的策略以提高最优解子路径被选择的概率，在粒子群算法的基础上给路径设置合理的优秀系数，以提高短边被选择的概率。在以上研究的启示下，本文对重复出现的排列段进行保留，只允许重复排列的起止点参加新的排序。通过这样的处理方法在一定程度上减小了排列组合优化问题的规模，缩小了群体搜索的可行空间，提升了个体在有限空间内的搜索效率，能更大概率地获得更优解。具体的构建过程如图1所示。

如图1 是对一个TSP 进行求解生成的两条路径d1和d2。两条路径中路段1-2-3-4 是重复出现的排列，第一步将重复出现的排列1-2-3-4 记录到m中（方便之后将整条路径还原）；第二步将城市2、3 从原城市集合中剔除；第三步对重复路段的起止点1-4 的距离设为0（为保证再一次求解过程中路段1-4能被选择）；第四步利用剩余城市的坐标和路段1-4 之间的特殊距离0 生成新的距离矩阵；最后运用常规智能算法在新矩阵下进行继续求解。

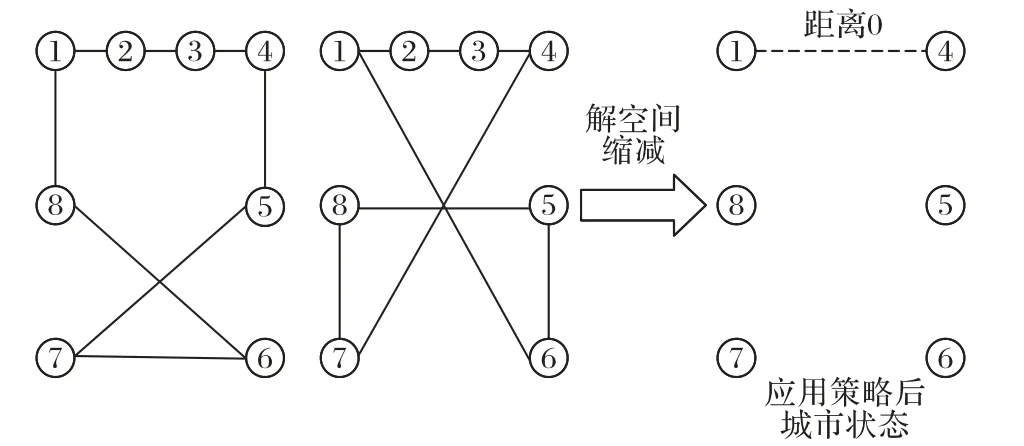
图1 解空间动态缩减策略Fig.1 Solution space dynamic compression strategy

本策略的编码和解码设计是针对结果特征，通过采用整数规则基于常规智能算法所求得路径对原问题的距离矩阵进行渐进式调整，以此达到空间缩减的目的，并未对常规智能算法搜索机制进行改变。因此在采用相同编码规则下，本策略可以应用于多种智能算法对类似问题进行求解，具有较好的适用性。

1.3 算法流程

本文改进算法流程如图2所示，具体的步骤如下：

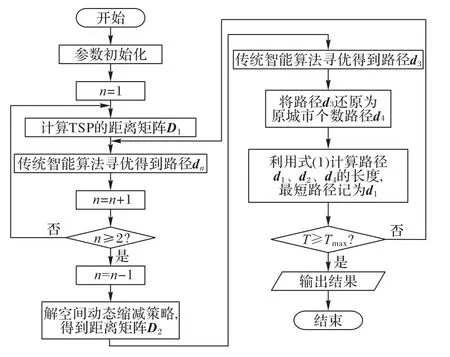
图2 改进算法流程Fig.2 Flowchart of the improved algorithm

步骤1 参数初始化，即设置相应算法所需要的参数。

步骤2 利用式（5）计算TSP的距离矩阵D1。式中：n为城市个数，a、b为城市坐标。

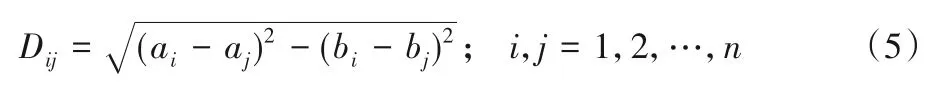
步骤3 利用智能算法g求解得到路径dn（g代指一种群智能算法，n为路径编号）。

步骤4 如果n不大于2，返回步骤3。

步骤5 将矩阵D1按照解空间动态缩减策略转换为D2。

步骤6 利用智能算法g对D2进行求解，生成路径d3。

步骤7 对d3利用m中记录的重复排列进行还原，还原为原始城市个数的路径d4。

步骤8 利用式（1）计算路径d1、d2、d4的长度，将最短的路径记为d1。

步骤9 判断是否达到终止条件，若达到则输出结果；若未达到则返回步骤3。

2 仿真实验与结果分析

2.1 改进算法效果验证

为了验证改进方法的有效性，本文分别对蚁群优化（ACO）算法、模拟退火（SA）算法、免疫算法（IA）改编为解空间动态缩减蚁群优化（Solution Space Dynamic Compression Ant Colony Optimization，SSDCACO）算法、解空间动态缩减模拟退火（Solution Space Dynamic Compression Simulated Annealing，SSDCSA）算法、解空间动态缩减免疫算法（Solution Space Dynamic Compression Immune Algorithm，SSDCIA）并用标准测试函数库TSPLIB 里面的5 个测试算例dantzig42、st70、eil101、pr144 和bier127 进行算法测试。蚁群算法的参数组合为：种群规模m=18，启发因子α=1，期望启发因子β=5，信息素挥发系数ρ=0.5，信息素强度Q=10，最大迭代次数Nmax=100；模拟退火算法的参数组合为：初始温度t0=120，最后温度t=1，温度衰减系数a=0.99，Markov链长度=5 000；免疫算法的参数组合为：群体规模NP=200，交叉概率Pc=0.5，变异概率Pm=0.1，克隆个数Ncl=10，最大免疫代数G=1 000。所有算法采用Matlab 2018a 实现，基于i5 CPU 2.50 GHz 处理器，4 GB RAM，操作系统为64 位Windows 10 系统平台进行测试。实验中针对单个算例，每个测试算法独立运行10 次，实验结果从平均值、最优值、最差值、方差及提升率进行统计学分析。

表1中理论最优值来源于TSPLIB 提供的最优值，原算法的值来源于每次改进算法原始矩阵下出现的最优值，提升率为改进算法相较于原算法平均值优化的程度。从表1中可以看出，算法SSDCACO、SA、SSDCSA 获得了比测试算例dantzig42理论最优值更好的解，SSDCSA在其他算例的测试结果也已接近理论最优值。总体上，运用本文提出的解空间动态缩减策略的三种改进算法无论是求解TSP效果比较好的模拟退火（SA）算法还是效果一般的免疫算法（IA）得到的最优值、最差值和平均值均要优于原算法，可见本文提出的解空间动态缩减策略的优越性。

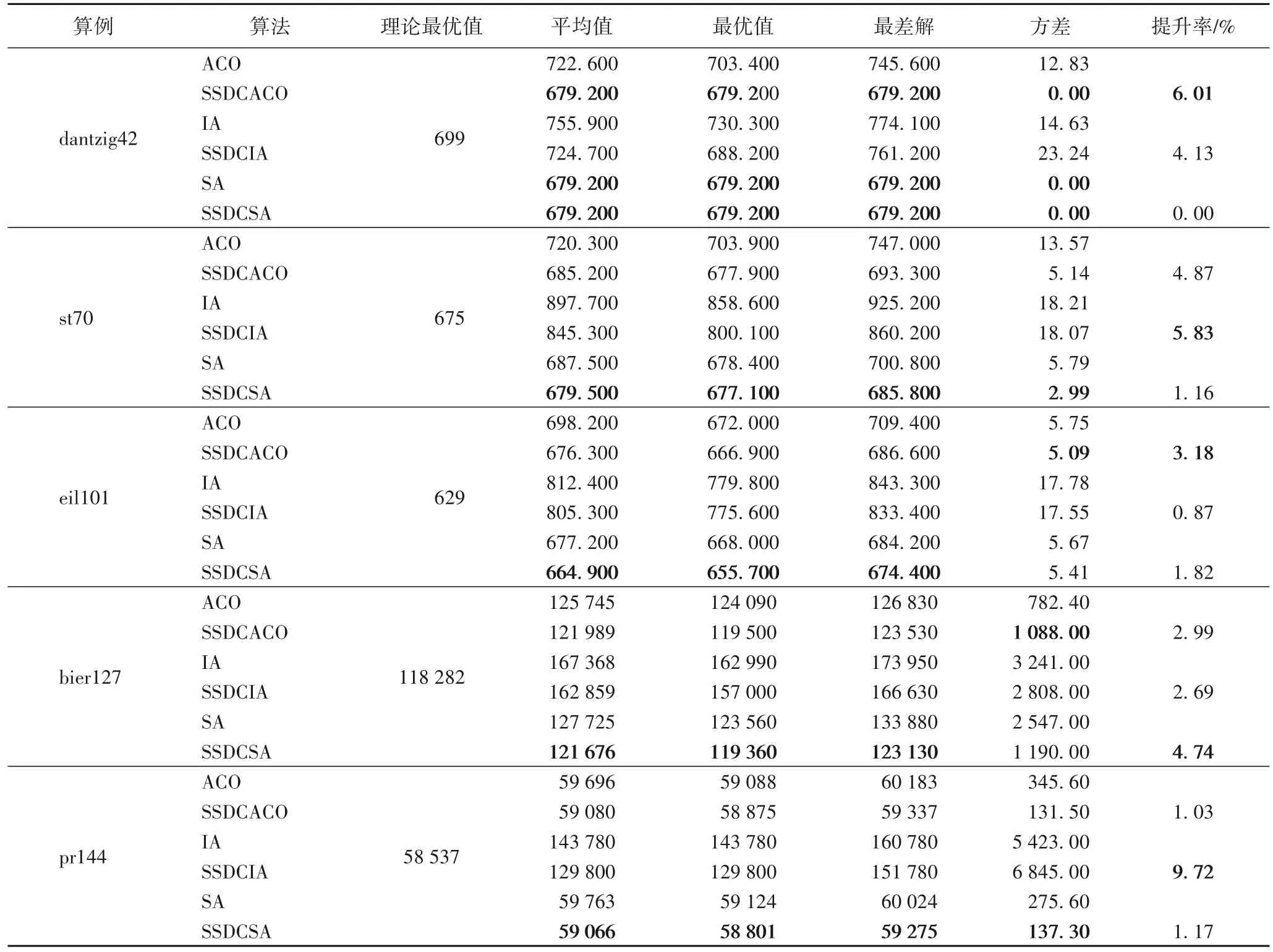
表1 仿真实验结果Tab.1 Simulation results

由于改进方法的步骤较原有的算法复杂，迭代次数和运算时间也明显增加。为了证明是改进方法使TSP 得到优化，本文做了进一步的比较分析，将dantzig42 问题运用原蚁群算法（ACO）和改进蚁群算法（SSDCACO）在相同迭代次数下进行结果比较。收敛曲线和优化路径如图3、图4所示。

图3中改进蚁群算法的收敛图像分为了五个阶段：

第一阶段 应用蚁群算法（ACO）对距离矩阵D1进行搜索，得到路径d1。

第二阶段 应用蚁群算法（ACO）对距离矩阵D1进行搜索，得到路径d2。

第三阶段 在路径d1和d2的基础上使用解空间动态缩减策略将原始距离矩阵D1转换为D2，然后采用蚁群算法（ACO）进行搜索，得到路径d3。

第四阶段和第五阶段 对第二阶段和第三阶段的重复。

图3中第三阶段和第五阶段应用解空间动态缩减策略后路径值均优于蚁群算法单独搜索，说明了应用解空间动态缩减策略的改进算法优于原算法；第五阶段的路径值优于第三阶段，说明了解空间动态缩减策略能在一次求解过程中多次运用；图3中还可以看出，在总迭代次数相同的情况下，改进算法的路径搜索结果优于原算法，说明了解空间动态缩减策略的有效性。

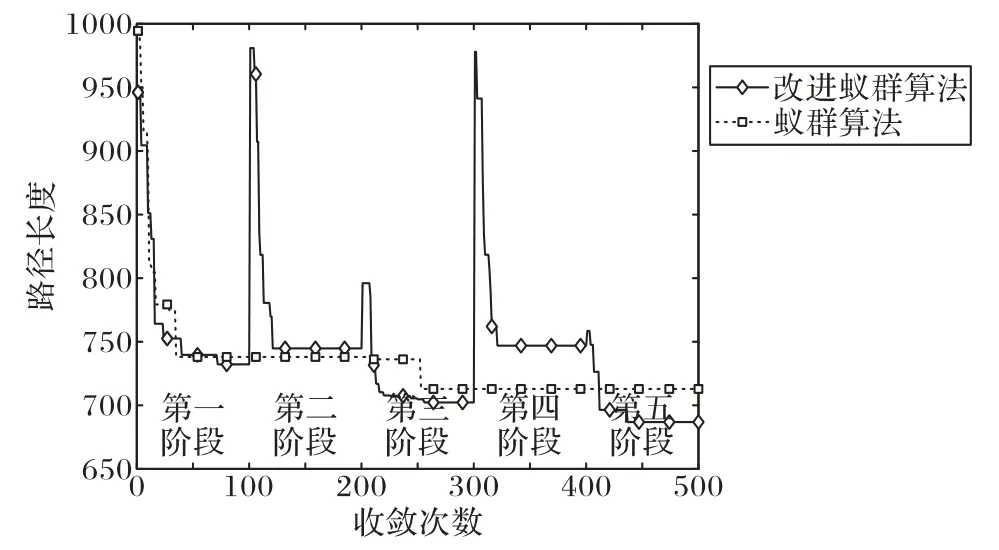
图3 改进前后蚁群算法收敛曲线Fig.3 Convergence curves of initial and improved ant colony optimizations

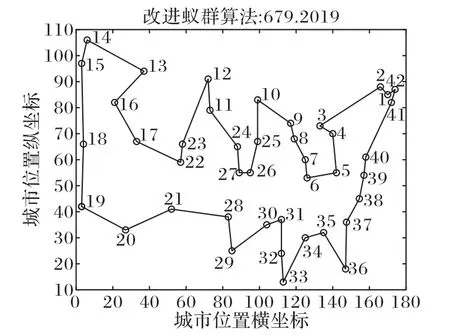
图4 优化路径Fig.4 Optimized path

2.2 重复排列长度对算法的影响

为了研究重复排列长度对解空间动态缩减策略有效性的影响，本文在编码时对最小重复排列长度做了区分，分别为2城市、3 城市、4 城市、5 城市，并在测试算例eil101、bier127 运用改进的蚁群算法做实验，实验结果如表2所示。

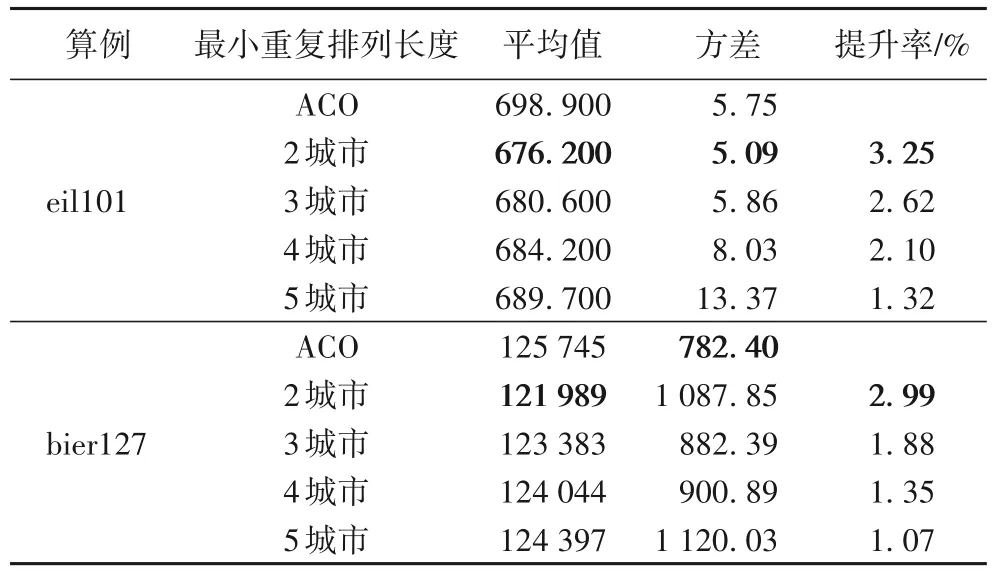
表2 最小重复排列长度对比实验结果Tab.2 Experimental results of minimum repeat permutation length

从表2中可以看出随着最小重复排列的长度增加，应用解空间动态缩减策略的改进蚁群算法对原算法的提升率逐步减小，方差呈增加的趋势，说明了不同长度的重复排列对算法优化均具有一定作用，并且当最小重复排列的长度增加时，使得改进算法的结果偶然性增大，算法的稳定性变差。

2.3 VRP算例验证

为了证明本文提出的方法同样适用于其他的排列组合优化问题，本文将解空间动态缩减策略应用于模拟退火算法（SA）对车辆路径优化问题（VRP）进行求解。算例来源于The VRP Web 里的测试算例A-n64-k9 和A-n80-k10。测试算法独立运行10次，仿真实验数据统计结果如表3所示。

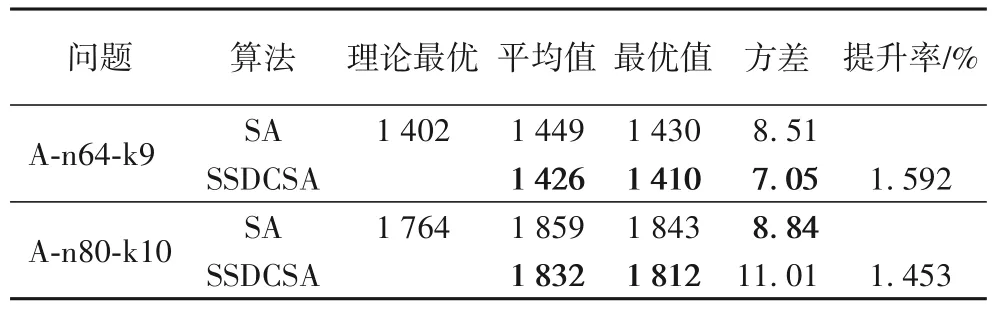
表3 VRP仿真实验结果Tab.3 Simulation results of VRP

从表3 结果中可以看出，基于本文提出新编码方式的改进算法作用于车辆路径优化问题与作用于TSP具有相同的效果，在最优值和平均值等方面均优于原算法，这也说明了本文提出解空间动态缩减策略对多种排列组合优化问题起作用，具有一定的通用性。

3 结语

本文针对一般群智能算法对大规模排列组合优化问题求解精度不高及时间过长的不足，提出了一种解空间动态缩减策略，逐步减小算法的搜索空间。在该解空间动态缩减策略中，基于在群智能算法两次求解，分析并融合解中重复片段，而后对剩余孤立片段再次求解，从而逐步减小群体搜索规模、节约算法搜索成本。通过将该策略用于多种群智能算法求解TSP 和VRP，得到的解均要优于原算法，表明解空间动态缩减策略适用于此类排列组合优化问题。本文所提算法在常规TSP 和VRP 等无约束或弱约束问题取得了较好的效果，对于复杂约束问题如带时间窗的VRP、柔性车间调度问题的应用将是今后研究的一个重点。