基于LPV系统的折叠翼仿生变形无人机模型预测控制方法研究

邵朋院，董彦非，李继广，屈高敏

(西安航空学院 飞行器学院，西安 710077)

0 引言

折叠翼仿生变形无人机可以像鸟类一样根据不同的任务需求来改变机翼形状[1]，例如在巡航飞行和机动飞行时采用不同的机翼形状。该优点使得折叠翼仿生变形无人机成为近年来的无人机领域研究热点[2-4]。

然而，在航空工业界至今仍然没有出现实用的折叠翼仿生变形无人机。究其原因主要是折叠翼仿生变形无人机在机翼变形过程中带来的非线性、非定常气动力以及参数变化和不确定性，这些都对建模和控制带来极大挑战[5]。在折叠翼仿生变形无人机变形过程控制中，当前多数采用基于固定构型的简化方法[4]，该方法忽略了变形过程瞬时动态(文中也称为暂态)对于飞机动力学的影响，实际上，暂态会对变形过程的稳定性造成不利影响[6]。研究人员可以通过线性变参数(LPV)系统进行暂态建模[7]，当前广泛采用的基于LTI系统的建模和控制方法很容易推广到LPV系统，所以基于LPV系统的控制方法成为折叠翼仿生变形无人机暂态控制中的研究热点[8-10]。但是，这些方法多是基于H∞的鲁棒控制方法，通过在变参数范围内进行网格划分可以从理论上保证在网格点处系统的稳定性和鲁棒性，然而无法保证整个变参数范围特别是非网格点处的鲁棒性和稳定性[11]。

模型预测控制(MPC)方法[12]通过在每一个控制步长内更新模型，来对系统的未来响应进行预测，而LPV建模方法可以通过变参数的实测值来对模型进行更新，所以MPC方法十分适合于进行LPV系统的控制。但是在当前LPV-MPC方法研究中，经常使用多胞形(polytopic) LPV模型[13-14]，多胞形LPV系统是通过多个顶点LTI系统的线性组合来近似表示LPV系统，通过针对顶点的LTI控制器线性组合来形成LPV控制器，所以该方法可以直接沿用LTI控制器设计方法，但是，通过以往研究[15]表明多胞形LPV系统无法准确表达折叠翼仿生变形无人机的系统模型。

在本文中，使用多项式参数依赖形式建立折叠翼仿生变形无人机的LPV系统模型，该模型不具有多胞形形式，文中给出了LPV系统的MPC控制设计方法，通过和非支配排序的遗传算法NSGA-II-PID的对比仿真，验证了LPV-MPC方法的有效性。

1 折叠翼仿生变形无人机的LPV系统建模

1.1 折叠翼仿生变形无人机的非线性模型

本文中研究的折叠翼仿生变形无人机样机图片如图1所示。折叠翼仿生变形无人机的外段机翼保持水平，而内段机翼可以绕着关节从0 deg(图1(a))到120 deg(图1(b))连续变形。折叠翼仿生变形无人机设计用来实现侦察和打击一体化(察打一体)功能。机翼展开构型可以低速巡航进行侦察，而折叠构型具有高速机动飞行能力，适合于进行发现目标后的打击和快速逃逸。

(a)机翼展开构型 (b)机翼折叠构型

折叠翼仿生变形无人机典型任务剖面如图2所示。任务开始为长机翼巡航构型，一旦侦察到目标，则开始折叠，并俯冲打击。在俯冲过程中，折叠翼仿生变形无人机俯仰角指令为-30 deg，折叠完成后进行高速平飞打击，打击完成后迅速展开机翼爬升逃逸，在爬升过程中，折叠翼仿生变形无人机俯仰角指令为-30 deg。所以，本文的研究关注于折叠翼仿生变形无人机变形过程的纵向动力学与控制。

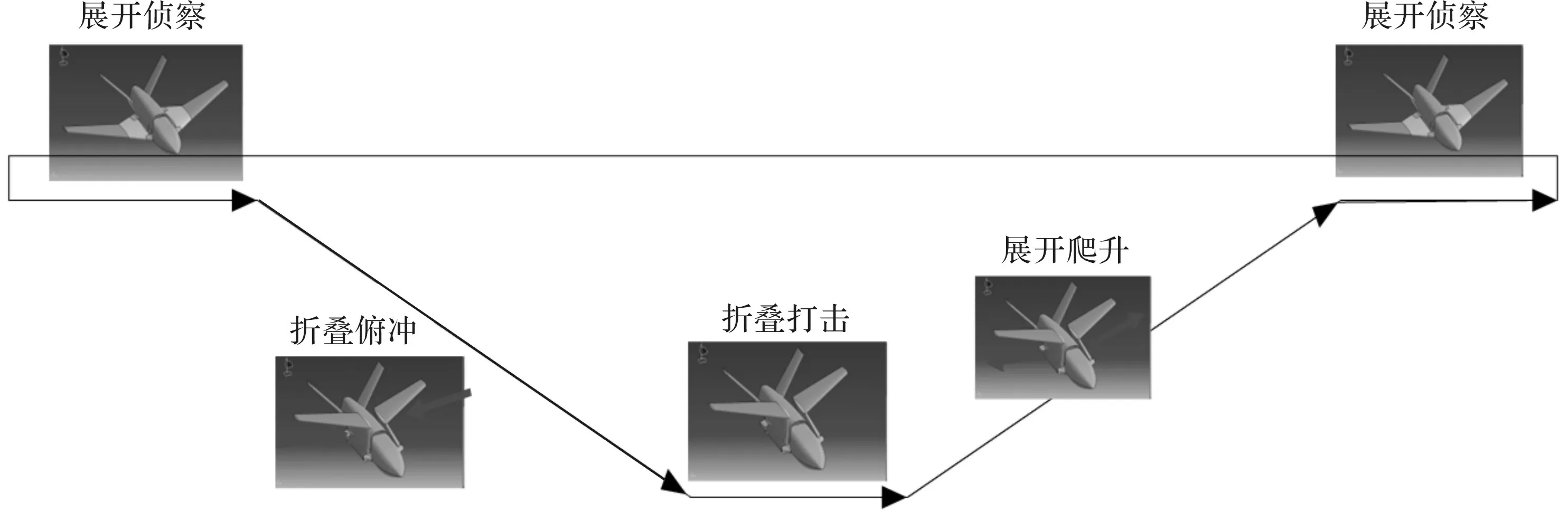
图2 折叠翼仿生变形无人机典型任务剖面

折叠翼仿生变形无人机的纵向非线性动力学数学模型如式(1)所示：

其中，u和w分别表示沿机体OX 和 OZ 轴的速度；q和Q分别表示俯仰角速率和俯仰角；Iyy是绕机体OY 轴的转动惯量；m表示飞机质量；g表示当地重力加速度；M是俯仰力矩；Fx和Fz分是除重力之外沿机体OX 和 OZ 轴的合外力，可以表示如下式：

其中，T、L和D分别表示发动机推力、升力和阻力；a是迎角。

假设发动机推力线沿着OX 轴，则上述变量可以写成：

气动系数CL、CD和Cm可以由CFD计算得到的气动数据库插值得到。记气动数据插值函数关系为：

C*=f*(v1，v2，…) (4)

其中，*表示气动力和力矩的项，如式(3)中的T、L、D和M等；f表示非线性映射函数；v1，v2，…是气动系数查表的列索引，例如，基本俯仰力矩系数可以写成Cm0=fm0(α，θr)，θr是折叠翼仿生变形无人机的机翼折叠角。因此，式(1) 实际上是一个非线性参数变化系统。

1.2 折叠翼仿生变形无人机的LPV系统建模

式(1)中的非线性模型可以表示成如下的非线性参数变化系统：

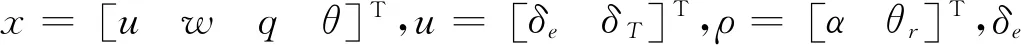
其中，x∈Rnx是系统状态，y∈Rny是系统的被控输出，u∈Rnu是控制输入，ρ∈Θ⊂Rnρ表示变参数集合。

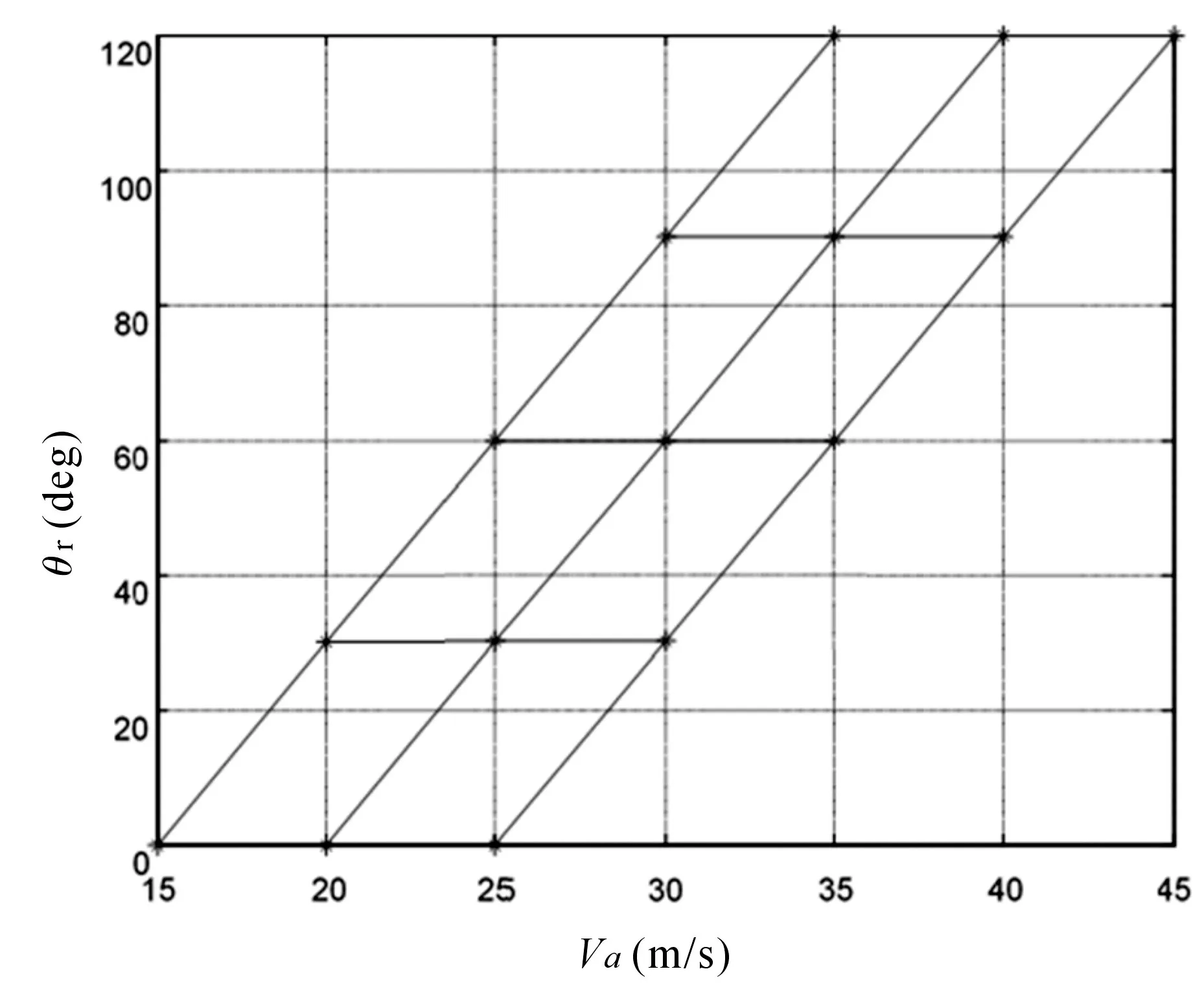
图3 折叠翼仿生变形无人机飞行包线数据

折叠翼仿生变形无人机飞行包线数据如图3所示。本文采用文献[8]中的改进函数替换法建立折叠翼仿生变形无人机的LPV系统模型，其中，变参数θr和Va取图3中网格点处的值，迎角a取网格处的配平迎角值。由于本文主要研究MPC控制方法，LPV系统建模步骤及结果请参考文献[8]。

2 基于LPV系统的MPC控制

2.1 LPV系统的MPC控制

将式(6)所示的LPV系统进行离散化，得到如下状态空间：

设预测步数为p，记参考轨迹为：

控制步数为m，控制量的增量序列为：

系统输出可以根据系统的LPV模型(7)获得，记为：

则MPC的控制目标函数为：

J(x(k),ΔU(k))=‖Γy(Yp,c(k+1|k)-R(k+1))‖2+‖ΓuΔU(k)‖2(11)

其中，Γy=diag{Γy,1,Γy,2,...,Γy,p}为跟踪误差的加权矩阵，Γu=diag{Γu,1,Γu,2,...,Γu,m}为控制代价的加权矩阵。

则MPC控制问题可以描述成如下优化问题：

对于LPV系统的MPC控制，文献[16]提出了一种基于线性矩阵不等式LMI(Linear Matrix Inequality，LMI)的MPC控制方法，在该方法中，通过在网格点处求解LMI来保证系统的稳定性，通过求解二次规划(QP)优化问题来进行状态预测。虽然QP问题可以通过有效的数学方法进行在线求解，但是在线求解LMI是不现实的，特别是对于网格化划分的LPV系统需要求解LMI组。

如果能将式(12)转化成为如下的QP问题，

s.t.Cz≥b(15)

则可以在线使用内点法[17]进行求解。

本文给出一种将式(12)转化为式(13)形式的方法，其步骤如下：

(1)将式(12)转化为式(13)

定义零输入控制误差变量为：

为简明起见，后文中将式(16)记为E。

将式(7)带入，则式(12)可以写成：

所以式(17)可以写成，

其中，

式(18)具有和式(14)一样的形式。

(2)将式(13)转化为式(15)

使用增量方式表示控制输入，则有：

u(k+1)=u(k-1)+Δu(k)+Δu(k+1) (20)

则，

u(k+1)≤umax(k+1)⟹-(Δu(k)+Δu(k+1))≥u(k-1)-umax(k+1) (21)

对于i=0，1，2，…，m-1，有

式(22)写成矩阵形式：

其中，

则式(23)具有和式(15)一致的形式，即可以通过QP求解。

2.2 在折叠翼仿生变形无人机中的应用

本文针对图2中的折叠翼仿生变形无人机典型任务剖面，使用基于LPV系统的MPC控制方法来设计变形过程中的纵向暂态控制器。LPV-MPC闭环系统结构如图4所示。其中，θr_cmd表示机翼折叠角指令，该指令按照图2中的典型任务剖面来设计。控制输入为升降舵和油门，即u=[δe，δT]T，输出为y=[θ,Va]T。控制输入限幅为δT∈[0，1]，δe∈[-30，30] deg。

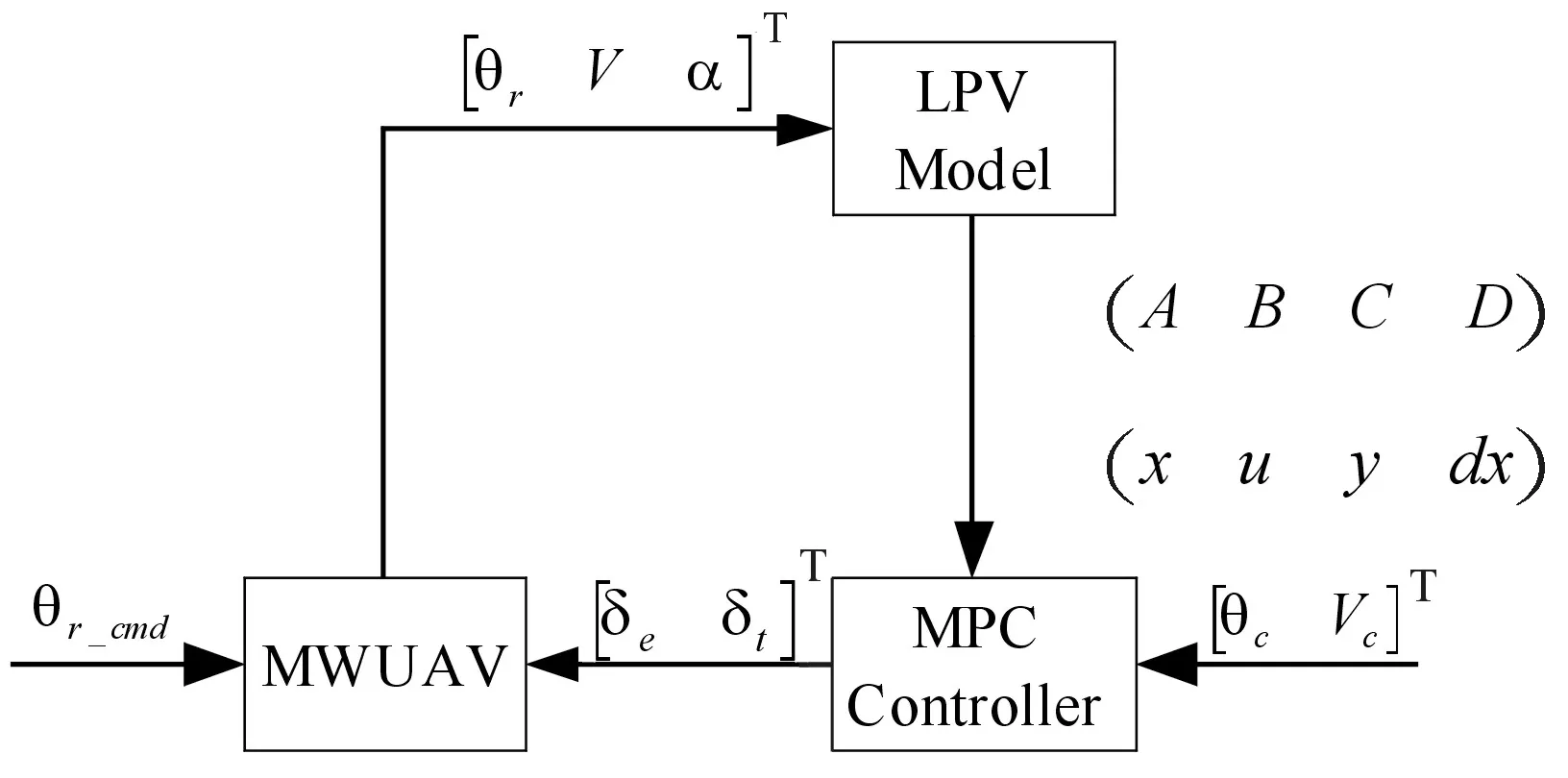
图4 LPV-MPC闭环系统结构

输入代价加权函数为：

控制误差加权函数为：

式(25)和式(26)表示控制的主要目标为跟踪俯仰角，其次为跟踪空速指令，并在跟踪的同时限制升降舵和油门在规定的范围内。采样周期为Ts=0.05 s，预测步数为p=200，控制步数为m=2。

空速和俯仰角参考指令设计如图5所示，空速和折叠角指令根据图3中的飞行包线数据来设计。

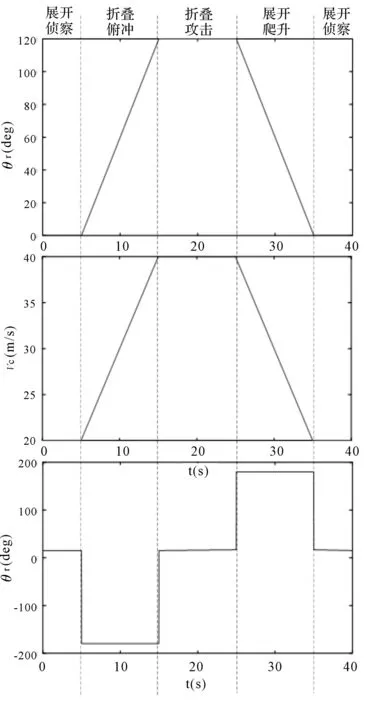
图5 参考指令设计

3 仿真和分析

使用文中给出的LPV-MPC控制方法和非支配排序的遗传算法NSGA-II-PID[18]做对比仿真。

仿真初始状态为展开构型下20 m/s平飞，配平迎角为2.8 deg。LPV-MPC控制和NSGA-II-PID控制的俯仰角指令和响应如图6所示，LPV-MPC控制和NSGA-II-PID控制的空速指令和响应如图7所示。从图6和图7可以看出，LPV-MPC控制方法比NSGA-II-PID控制方法有更好的跟踪准确性，特别是对于俯仰角的跟踪，稳态误差在2 deg以内，空速跟踪因为权重较小，所以综合比较LPV-MPC控制方法比NSGA-II-PID控制方法准确性高。

图6 LPV-MPC控制和NSGA-II-PID控制的俯仰角指令和响应

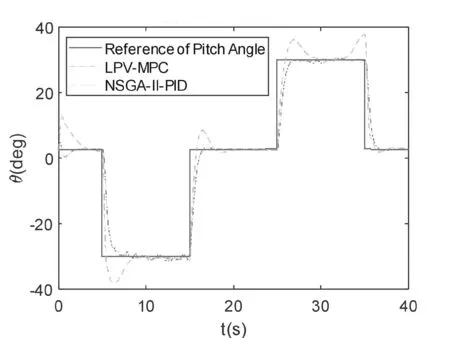
图7 LPV-MPC控制和NSGA-II-PID控制的空速指令和响应

LPV-MPC控制和NSGA-II-PID控制的升降舵控制输入如图8所示，LPV-MPC控制和NSGA-II-PID控制的油门控制输入量如图9所示。从图8可以看出，LPV-MPC方法的升降舵输入量可以约束在10 deg以内，而NSGA-II-PID控制方法约束在15 deg以内，图6中显示出LPV-MPC方法跟踪准确性更高，所以具有更高的控制效率。图9中NSGA-II-PID的油门输入量维持在最大值1或者最小值0处，其原因是按照控制律算出的输入量超过了0～1的范围，就有可能是约束失败，而LPV-MPC控制方法都在0～1之间，所以其控制输入约束和控制调节更有效率。

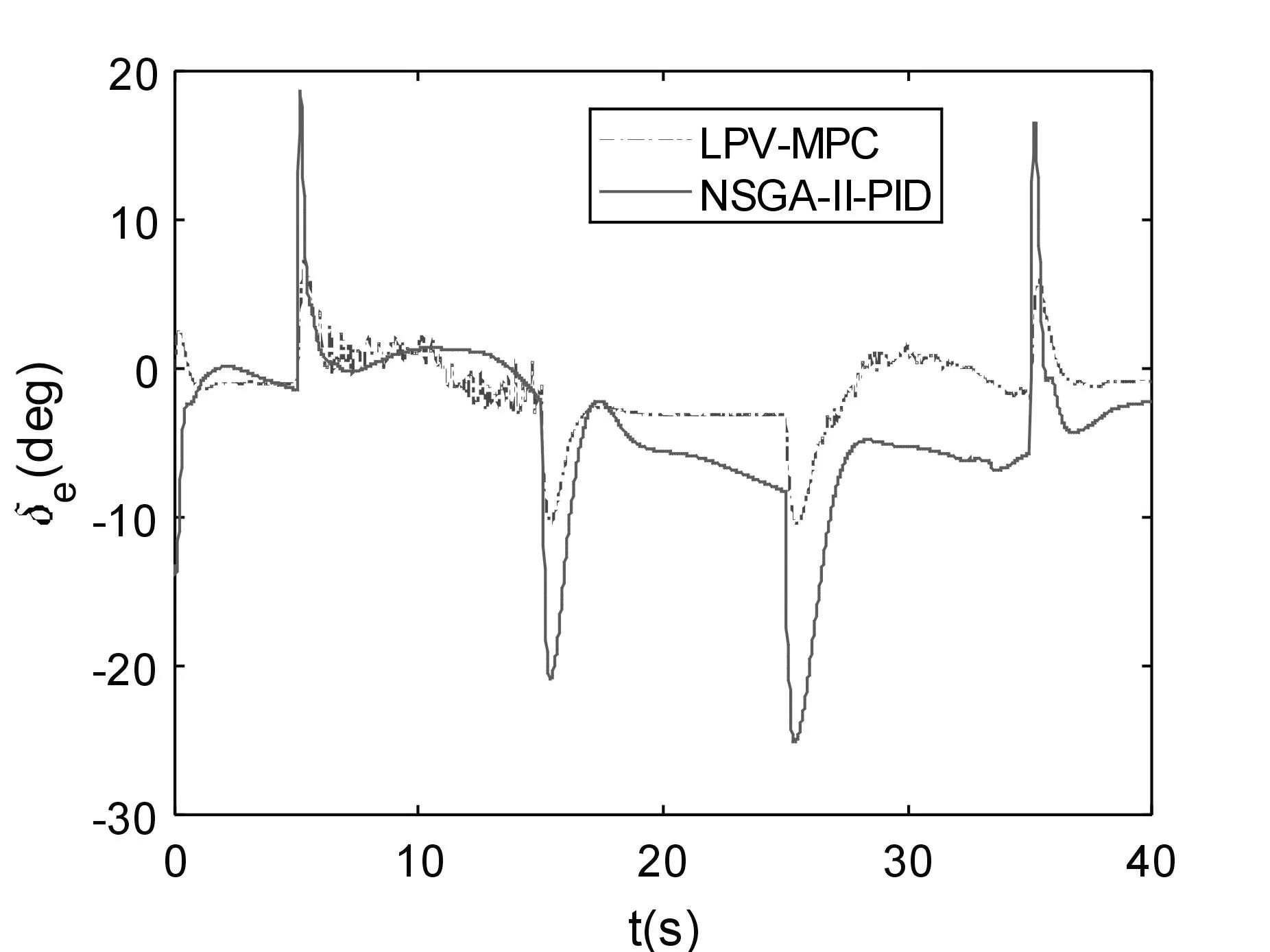
图8 升降舵控制输入

图9 油门控制输入量

4 结语

本文基于LPV系统的MPC控制方法设计了折叠翼仿生变形无人机变形过程的纵向暂态控制器，将LPV系统的MPC控制问题转化为QP优化问题，从而可以使成熟的数值算法在线求解。通过仿真将该设计方法应用在折叠翼仿生变形无人机纵向暂态控制中，与基于NSGA-II-PID的增益调度方法进行了对比，结果表明该方法具有更好的跟踪准确性和更高的控制效率。