某发动机飞轮连接圈固定螺栓连接可靠性分析
王德成,高建红,刘伦伦,曾超,段良坤,程市
(内燃机可靠性国家重点实验室,潍柴动力股份有限公司,潍坊 261061)
0 引言
在装载机、推土机、铲运机等非道路机械行业,液力变矩器广泛应用,发动机产生的动力由飞轮传递到液力变矩器后经变速箱传递到车桥[1]。为满足不同平台发动机与主机厂之间的配套需求,减少主机厂底盘零部件变动,非道路通常设计不同长度和直径的飞轮连接圈,实现发动机飞轮与液力变矩器之间的连接装配。飞轮连接圈与飞轮之间采用螺栓连接,螺栓规格、数量、螺栓布置等影响连接的可靠性。
某发动机配套新平台装载机,其需求功率降低,飞轮转动惯量减小,曲轴传动系统其余部件不变。考虑到发动机输出扭矩减少,整机厂提出降成本措施,建议将飞轮连接圈固定螺栓数量减少,为此,需仿真分析评估螺栓的连接可靠性。
本文通过建立曲轴系扭转振动模型,获得了指定爆发压力下飞轮端的最大输出扭矩;并通过有限元分析软件仿真了最大输出扭矩下飞轮与飞轮连接圈的相对滑移量;然后,根据仿真结果,确定了螺栓组布置方案的合理性。
1 飞轮连接圈简介
配套新平台装载机某发动机,其曲轴传动系统结构如图1所示。
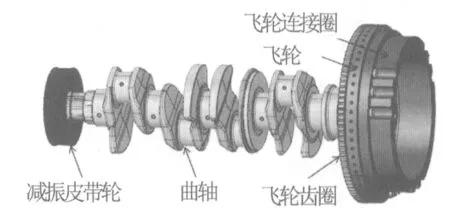
图1 曲轴传动系统三维模型
该发动机的飞轮连接圈与飞轮采用9个螺栓连接。整机厂建议将发动机飞轮连接圈固定螺栓数量由9个减少为6个。飞轮连接圈固定螺栓位置及建议减少的3个螺栓位置如图2所示。

图2 飞轮连接圈螺栓孔位置
2 飞轮端输出扭矩分析
EXCITR Designer软件包含了发动机轴系设计初期所需要的模块,将轴系各部件简化为惯量点和轴段,输入数据相对较少,可进行曲轴疲劳强度分析、轴承分析、扭转振动分析等,是发动机设计的重要工具[2-3]。
2.1 曲轴扭转振动模型搭建
本文基于EXCITR Designer软件,对某直列4缸发动机建立曲轴扭转振动模型,搭建的发动机轴系扭转振动计算模型包含的元件有:发动机、活塞、连杆、轴瓦、减振器、连接副等。通过设置发动机转速、气缸数、缸径行程、连杆长度等全局参数,将各运动副按机械运动关系连接,得到曲轴系扭转振动计算模型,如图3所示。

图3 曲轴系扭转振动模型
输入发动机爆发压力参数,其中爆发压力曲线要求是,尽量覆盖发动机从怠速到额定转速的整个转速区间,如图4所示。

图4 发动机爆发压力
2.2 曲轴扭转振动仿真结果
在仿真控制面板上,选择“Torsion”任务项,得到仿真结果,如图5~6所示。从图5可以看出,发动机曲轴系统的1阶频率为196.2 Hz,高于该发动机额定转速2 900 r/min时所对应的4谐次主激励频率193 Hz,模态满足要求,轴系共振风险较小,共振引起曲轴系统螺栓失效风险小。从图6可以看出,飞轮端扭转振动传递的最大扭矩为4 980.17 Nm,其对应的发动机转速为2 400 r/min。

图5 曲轴系固有频率
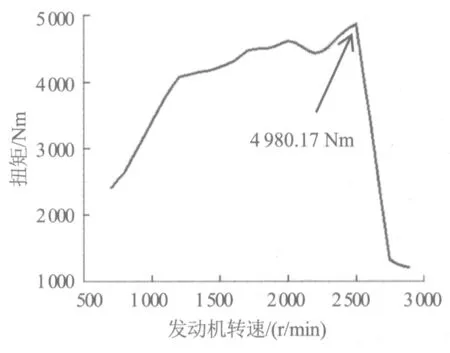
图6 飞轮端螺栓传递扭矩
3 有限元仿真分析
3.1 有限模型建立
利用有限元前处理软件Hypermesh,对曲轴系总成各零部件进行网格划分,曲轴截取最后1个主轴颈作为边界,对计算影响不大的几何细节(倒角、倒圆、工艺孔等)做了局部修改和简化[4],网格大小平均为4 mm,模型共包含网格数量为425 354个,节点数量为145 709个,网格模型如图7所示。
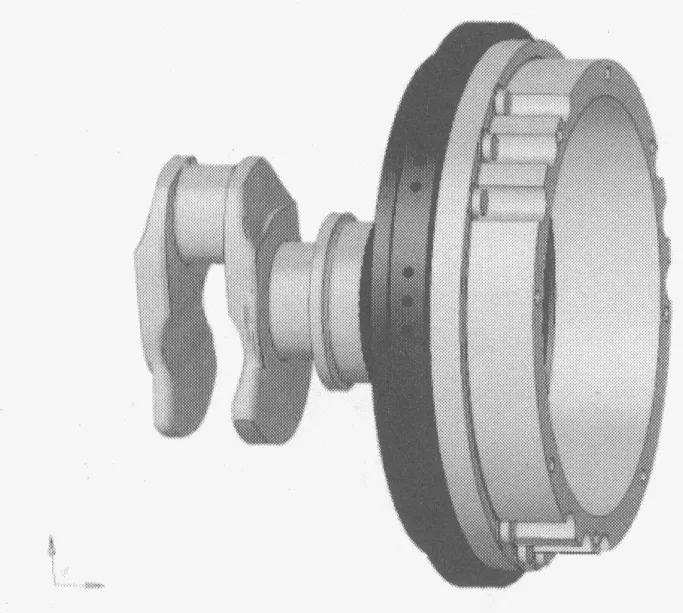
图7 仿真分析网格模型
3.2 边界条件及螺栓预紧力
螺栓装配时,应保证被连接结构承压面不发生压溃,螺栓预紧力不超过屈服预紧力的85%。该发动机飞轮连接圈螺栓主要参数如表1所示。

表1 飞轮连接圈螺栓参数
螺栓预紧力的计算公式如下[5]:
(1)
式中:A为螺栓截面积,mm2,取84.5 mm2(公称应力截面面积和最小直径对应的截面面积中取最小值);v为常量,取1.0;σ为材料屈服强度,MPa,取940 MPa;p为螺栓螺距,mm,取1.5 mm;d0为螺栓最小直径,mm,取10.37 mm;d2为螺纹中径,mm,取11.03 mm;μ为摩擦系数,取最大值0.12。
代入各参数,计算得到飞轮螺栓的最小预紧力为75.73 kN。
边界条件设置为,约束主轴颈轴承接触区域节点的6个方向自由度,如图8所示。螺栓与连接圈、连接圈与飞轮、飞轮与曲轴之间建立摩擦接触,摩擦系数取0.13。对需要考察滑移量的区域建立nodeSet点集,如图9所示。施加螺栓初始预紧力、螺栓预紧力、旋转离心力及飞轮端扭矩4个载荷增量步,对曲轴传动系统进行仿真分析。

图8 边界约束条件

图9 nodeSet点集合
3.3 有限元仿真结果
在Abaqus软件中,滑移被定义为一种累积的相对移动,是相对位移矢量增量和局部切线方向的积。接触分析中,结构在外界载荷的作用下,从面节点相对于主面产生位移。计算结束后,各个分析步中相对位移的总和被储存在CSLIP1和CSLIP2中。
引用节点集nodeSet的CSLIP1和CSLIP2数据,计算合成接触面上的实际滑移量SR。计算公式如下:
(2)
式中:SR为实际滑移量,mm;S1i和S2i分别为第i分析步中滑移平面内2个方向的滑移量,mm。
仿真完成后,提取nodeSet点集处滑移量。结果显示,原方案9个螺栓固定,飞轮和飞轮连接圈之间的最大滑移量为0.009 mm,出现在528 497节点处,如图10所示。去掉3个螺栓的新方案,最大滑移量为0.01 mm,对应节点位置与原方案相同,如图11所示。

图10 原方案nodeSet点集处滑移量

图11 新方案nodeSet点集处滑移量
新方案与原方案相比,飞轮和飞轮连接圈之间的滑移量指标增加约10%,但2种方案均满足滑移量不超过0.01 mm的设计标准,因此可以采用新方案,实现降成本目的。
4 结论
飞轮连接圈用于传递飞轮输出扭矩,是发动机动力传动系统上的重要部件,直接影响整车的动力性能。
飞轮连接圈的固定螺栓,其布局、数量、规格、等级等因素对其连接可靠性有直接影响。为降低成本,可以根据实际应用中的载荷扭矩,适度减少连接螺栓数量,但必须对螺栓连接的可靠性进行分析。

