应用于硅基OLED微显示器的分段可调伽马校正

黄振兴， 黄 苒， 赵博华*， 苏 畅， 杜 寰

(1. 中国科学院 微电子研究所，北京 100029; 2. 中国科学院大学，北京 101408)

1 引 言

硅基有机发光二极管(OLED)微型显示器是一种近年来随着VR/AR技术的发展而成为显示领域研究热门的新型显示器，将有机发光二极管直接与单晶硅集成电路集成，以单晶硅作为OLED发光器件的基底，且利用成熟的CMOS工艺完成发光器件的像素驱动和外围驱动系统[1]。

伽马校正最初起源于阴极射线管(Cathode Ray Tube, CRT)显示器中电光转换的非线性[2]，射线管产生的电子束及其生成的图像亮度与输入电压呈指数的对应关系。而对于OLED显示器，发光亮度与流过OLED器件的电流是线性的，但实际上人眼视觉系统对于亮度变化的感觉也是非线性的[3]。伽马校正正是为了克服这种非线性而引入的一种传输函数，在视频流、计算机图形学以及其他成像系统中应用广泛。流行的伽马矫正方法有两种：一种是对显示系统的伽马特性进行数字建模，计算出矫正后的视频驱动数据，预先存储在存储器中，显示过程中采用查找表法(Look Up Table, LUT)实现图像的伽马矫正，该方法为数字校正，但需要占用较大的存储空间[4]；另一种方法是利用驱动电路外围的精密电阻和运算放大器组成灰度级电压产生电路，提供多级参考电压，与显示驱动电路一起实现图像信号的伽马矫正，该方法相当于采用了非线性数模转换器(Digital to Analog Converter, DAC)实现，随着灰度级数的增加，额外需要的模拟电路复杂程度也大大增加[5]。本文基于第一种方法提出适用于硅基OLED微显示器的数字伽马校正方法，该校正方法在精度和实现面积上均较传统方法有一定优势，且可以实时根据OLED发光情况对显示器进行校正，对于显示器显示质量的提高具有重要意义。

2 伽马校正原理

2.1 显示驱动系统的构成

显示器不同亮度的实现可以主要分为空间灰度调制、时间灰度调制以及幅值灰度调制3种方式。空间灰度调制是指从像素单元的发光面积对灰度阶梯进行控制；时间灰度调制是指在单元时间内控制像素的发光时间长短来对灰度进行控制；幅值灰度调制是通过控制显示器件的驱动电压或驱动电流大小从而控制灰度。我们选择的是通过幅值灰度调制控制OLED发光的亮度。图1为微显示芯片显示驱动系统的结构[6]。它主要由视频数据处理模块、线性数模转换器、像素驱动电路以及OLED阵列组成。视频数据处理模块接收来自芯片外的视频信号进行处理并产生控制微显示芯片正常工作所需的各种时序信号，DAC将数字视频信号线性转换成对应的模拟电压，像素驱动电路根据该电压控制OLED器件的发光亮度。

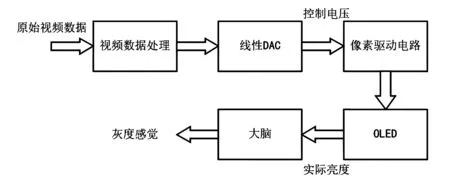
图1 显示驱动系统的结构Fig.1 Structure of display driving system

2.2 伽马校正的原理

对于某一灰度级别的显示，视频数据若不进行伽马校正处理，OLED器件的发光亮度与输入的视频数据的灰度值呈线性关系。而通过人眼视觉系统我们的大脑感受到的灰度级别实际上与发光器件的亮度呈1/γ的指数关系，即

Y=K1·L1/γ，

(1)

其中:L为实际发光亮度，Y为大脑感受到的灰度级别，K1为常数。在低亮度环境中，人眼对亮度变化敏感，能够感知很小的亮度差异；在高亮度环境中，对亮度变化不敏感，亮度值变化较大时，人眼才能分辨，这种特性称为人眼的伽马特性[7]。因此，大脑感受到的灰度级Y与输入视频数据的灰度值X也呈1/γ的指数关系。

为了保证对于均匀变化的灰度级别大脑能够获得均匀变化的亮度感受，需要对原始的视频数据进行伽马校正处理。伽马校正其实是一种为了克服大脑对于亮度变化的非线性感受的一种传输函数，其表达式为

G=K2·Xγ，

(2)

其中：X为原始的视频数据，G为通过伽马校正后的输出视频数据，K2为常数。校正后的数据通过显示器发光的实际亮度为

L=C·Xγ，

(3)

将式(3)代入式(1)则有：

Y=K3·X，

(4)

上式C和K3均为常数。因此通过对原始视频数据进行伽马校正处理，使得我们的大脑感受到的灰度级别与视频数据的灰度级别为线性关系，达到了我们的校正目的。上述伽马校正的推导过程如图2所示。

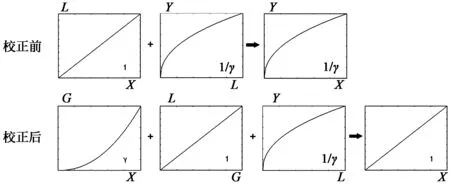
图2 伽马校正的原理Fig.2 Principle of gamma correction

3 分段可调伽马校正的实现

3.1 位宽拓展实现非线性

基于前面的显示驱动系统，由于DAC的参考电压确定，最大灰度数据对应的OLED驱动电压也是确定的。也就是说，对于伽马校正前后的两组数据，对应的最小驱动电压和最大驱动电压是相同的。如果想完成从输入数据到输出数据的非线性映射，需要对输出数据进行位宽拓展[8]，则低位宽数据的中间码值可以对应的是多个高位宽数据的中间码值，如图3所示。但是要求低位宽数据与高位宽数据之间的映射无交叉，通过这样的映射关系，可以保证随着输入数据的递增输出数据也是递增的，但是增加的幅度是可以调整的，这样就实现了非线性映射。

图3 位宽拓展示意图Fig.3 Diagram of bit width extension

下面用4 bit映射到6 bit的数据来说明如何通过位宽拓展来实现非线性。4 bit数据与6 bit数据之间的一一映射如表1所示。图4所示的曲线横轴表示4 bit输入数据，纵轴表示6 bit输出数据，拓展的位宽越多，输出曲线能够更加平滑。从图4可以看到通过位宽拓展可以很好地实现非线性。

表1 4 bit数据到6 bit数据映射关系Tab.1 Mapping relations between 4 bits and 6 bits data

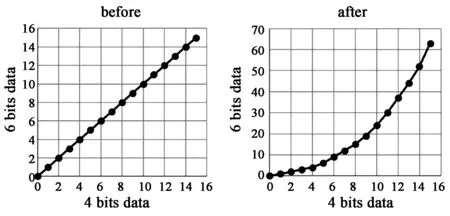
图4 4 bit数据到6 bit数据映射曲线Fig.4 Mapping curves of 4 bits and 6 bits data

3.2 可调分段拟合伽马曲线

对于我们的一款XGA039单色OLED微显示芯片，分辨率为1 024×768，输入数据为8 bit，表示的灰度值范围为0～255。我们将输入数据进行位宽拓展到10 bit来实现非线性。通过查找表的方式完成低位宽数据到高位宽数据的映射，是实现伽马校正最简单直接的方式[9-10]。但是若对256个灰度级数据进行查找表操作，且输出为10 bit，则实际需要的RAM存储空间的大小为256×10 bit，即需要256个位宽为10 bit的寄存器，这对于芯片实现来说太过于耗费面积[11]。若将伽马校正曲线用17个点来拟合，相邻两点之间的曲线近似为直线，就得到了16段线性分段函数。由于通过位宽拓展获得的10 bit数据的最大值和最小值已经确定，即对应OLED的最大发光亮度和最小发光亮度，所以仅需要通过设置中间的15个点来控制伽马曲线的形状。

由于人眼的伽马特性，在低亮度环境下对灰度级变化敏感，在高亮度环境下对于灰度级变化不敏感，我们希望在低亮度区域用更多的灰度级来实现拟合，达到更高的精度。基于这种考虑，在选择上述的用于拟合曲线的15个点时，可以不以等间距选择相邻两点对应的输入灰度级，而是在低灰度级区域选择更多的点，高灰度级区域选择少数几个点。使用I2C总线配置模块内部寄存器的值来选择这15个点在伽马曲线中的位置，这样使得伽马曲线拟合的分段情况可调，在芯片制作完成后可以根据实际OLED的发光情况调整伽马曲线的形状，以此获得更好的显示效果[12]。

上述15个中间灰度级对应的输出值通过LUT操作获得；而对于相邻两点之间的灰度级，首先需要判断该点位于哪两点之间，然后通过线性插值计算获得输出，计算公式为

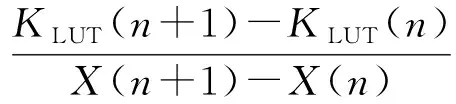
(5)

其中KIN为8 bit输入数据，KOUT为10 bit输出数据，X(n)与X(n+1)为KIN相邻两点的输入灰度值，KLUT(n)与KLUT(n+1)为这两点对应输出值，这4个参数值均通过I2C总线配置。这样的插值计算不仅满足实际伽马校正的精度需求，且需要的寄存器数量仅为15个点所对应输入和输出值的数据位宽，大幅减小了实现面积。

4 实验调试与结果

4.1 实验调试过程

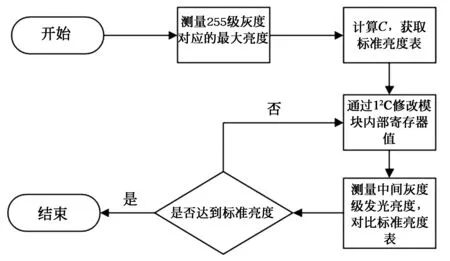
图5 伽马校正调试流程Fig.5 Gamma correction debugging process

根据式(3)得发光亮度L与原始视频数据X的γ幂次成正比关系，比例系数为C。γ的取值一般在1～4之间，取1意味着没有校正，输入输出保持直线关系，图像质量没有改善。取值越大，图像的暗区灰度等级越细腻，黑白反差也变大，但γ取值过大图像整体质量下降，所以一般取1.6～3.4 之间，实践中取1.6、2.2、2.8、3.4 这4个值进行调试比较合适[13]。对于一个确定的γ取值，调试过程如图5所示。

4.2 结果

针对上述的调试过程，我们的XGA039 OLED微显示器实际发光的最大亮度为20 000 cd/m2，γ取值分别为1.6，2.2，2.8，3.4四个值时的亮度L与原始数据灰度值X的关系曲线如图6所示。根据实际的显示情况，在γ=2.2时获得最适应人类视觉系统感知的显示效果。

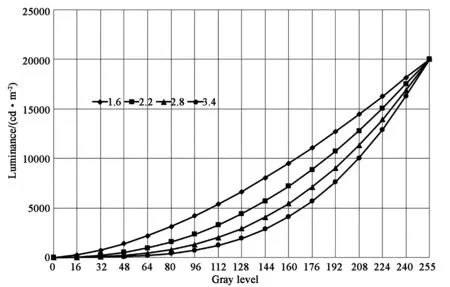
图6 不同γ取值的伽马曲线Fig.6 Gamma curves with different γ

上面的4簇曲线是在将伽马曲线均匀分段的情况下测得的，为了更好地拟合γ=2.2时的曲线，采用了可调分段拟合的方法，即在低灰度级选择更多的点。具体分段方式如图7所示，低灰度级区域相邻两点对应输入灰度级的间距为8或16，高灰度级区域相邻两点对应输入灰度级的间距为16或32，即中间15个灰度级的选择为8, 16, 24, 32, 40, 48, 64, 80, 96, 112, 128, 144, 160, 192, 224，测试实际校正数据如表2所示，通过伽马校正在低亮度区域对应了更高的灰度级。这样，如图8曲线在低灰度区域的放大图所示，在人眼更为敏感的低亮度区域达到了更高的拟合精度。当显示一张包含256个灰度级逐渐变化的图片，通过这种方法校正前后芯片的显示效果对比如图9所示，校正之后灰阶的变化明显，更适应人眼感知的需求。

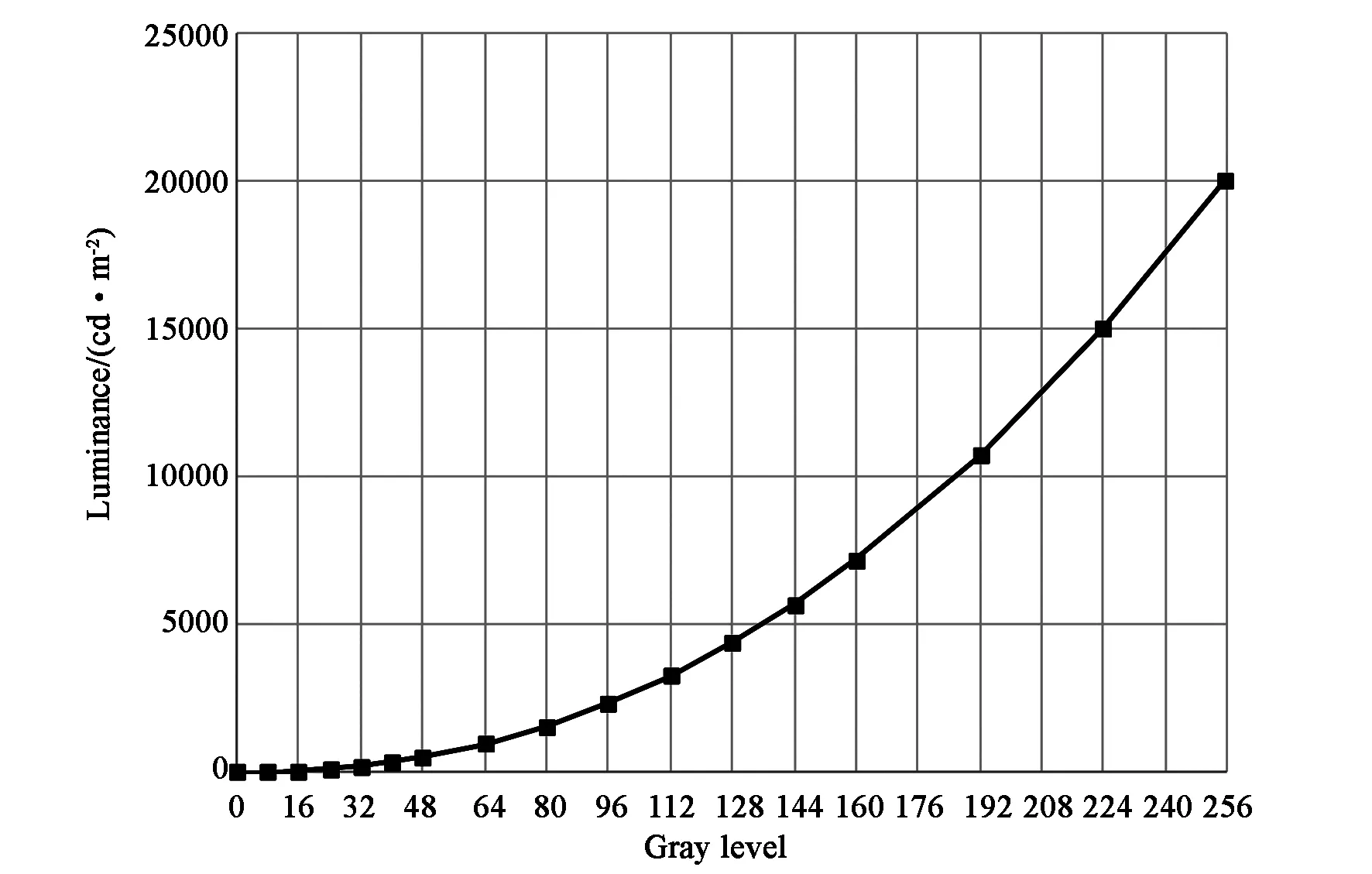
图7 γ=2.2时采用可调分段拟合的伽马曲线Fig.7 Gamma curve with adjustable segmentation of γ=2.2

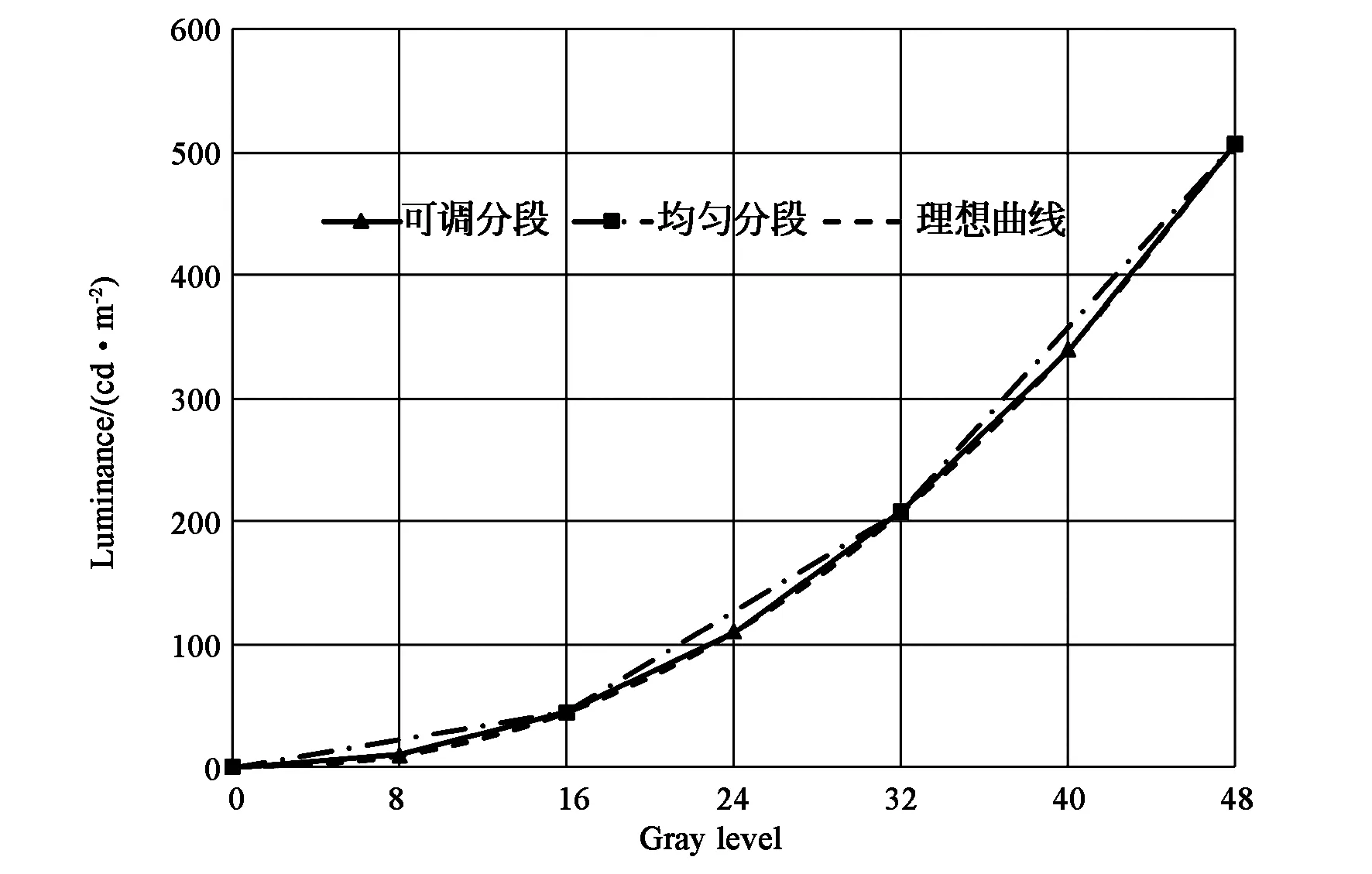
图8 低灰度区域伽马曲线放大图Fig.8 Magnified view of gamma curve in low gray level region

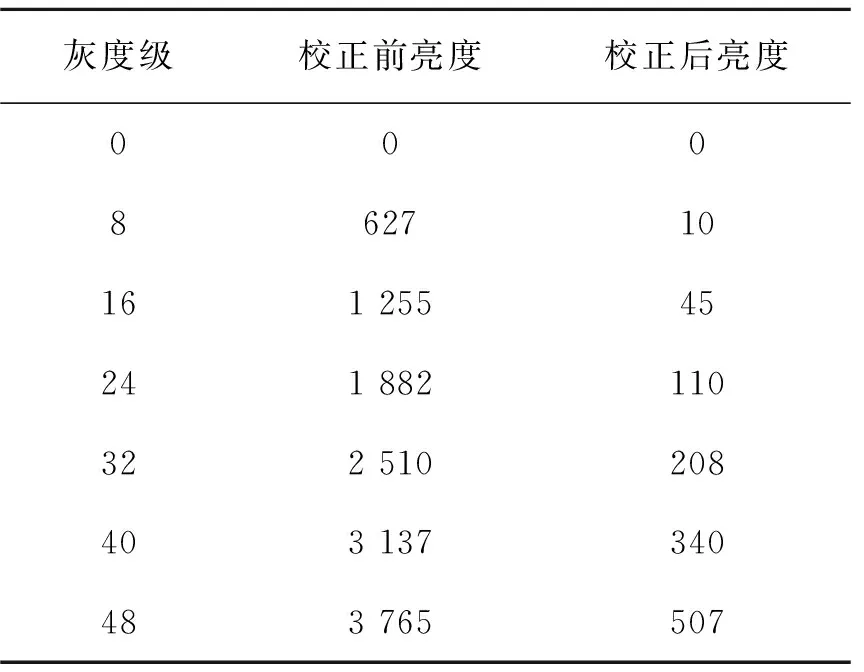
表2 灰度级-亮度测试数据Tab.2 Gray-luminance test data (cd·m-2)

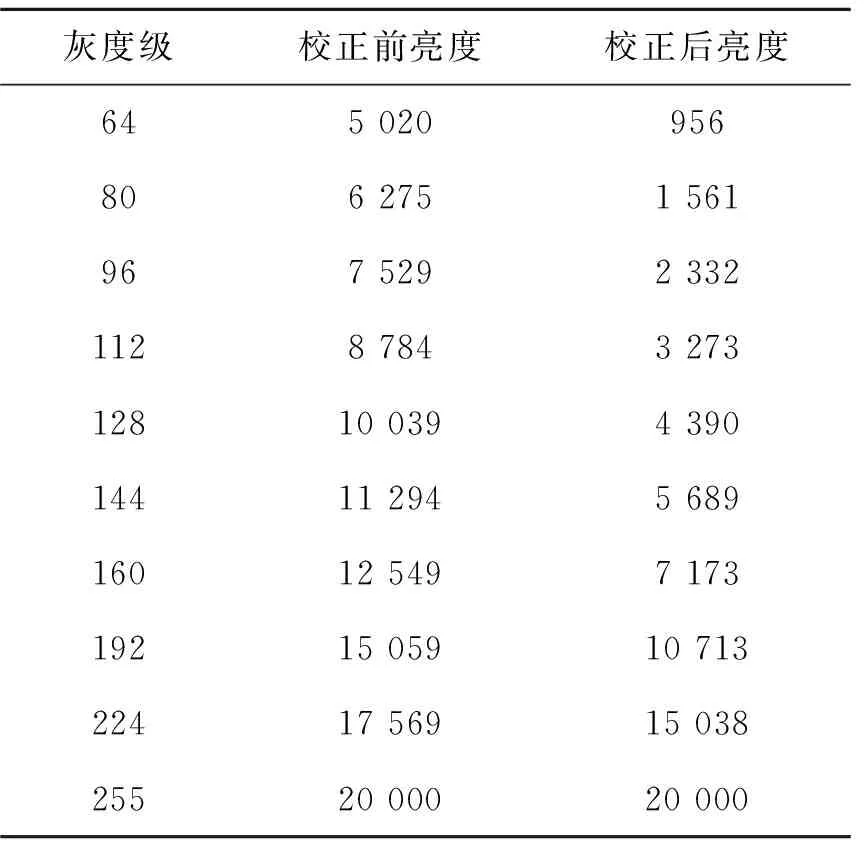
续 表

图9 伽马校正前后对比Fig.9 Comparison before and after the gamma correction

5 结 论

本文提出了一种适用于硅基OLED微型显示器的数字伽马校正方法，用于改善人眼视觉系统对于亮度感知的非线性。该非线性函数通过分段线性函数拟合而成，基于查找表和线性插值算法实现，并且通过I2C总线配置内部寄存器值，根据实际发光情况做到分段可调，可在低亮度区域获得更高的校正精度以适应伽马特性。相对于传统的数字查找表法不仅提高了在低灰度区域的精度而且大大节省了实现面积；而相对于使用非线性DAC的模拟校正方法，外围模拟电路的复杂程度也得到降低。在使用XGA039芯片进行实际发光调试下，测得的最大发光亮度为20 000 cd/m2，当伽马系数取值为2.2时，分段方式采用可调非均匀分段时获得了较为适应人眼视觉系统感知的显示效果。