基于DISTMESH的三角形网格自适应生成方法与应用
张靖婷王宪业李 铖葛建忠*
(1.华东师范大学 河口海岸国家重点实验室,上海201100;2.上海市海洋环境预报中心,上海200062)
海洋数值计算的基础与核心是在时间和空间上对流体动力学方程进行离散。在计算区域中,水平方向空间离散而成的平面网格,主要分为结构、无结构和混合网格[1]。当前主流的海洋数值模式中,DELFT3D[2],ROMS[3],POM[4]等模式采用了结构网格,常用正交或非正交曲线网格,TELEMAC[5],FVCOM[6]等模式采用了无结构网格,网格单元为三角形,DELFT-FM[7]模式采用了混合网格。结构网格计算高效,在简单区域能充分发挥优势,但其对复杂区域的几何拟合度较差。无结构网格能较好地拟合不规则边界,方便局部加密,且能迅速改变分辨率,适用范围更广,尤其针对复杂区域,无结构网格更具优势。
海洋数值计算时,经常需要离散边界不规则、地形多变的复杂区域。这些区域的网格生成,不仅应保证各个单元的质量,还应合理控制分辨率,在岸界、地形显著变化处生成小单元,保证离散的几何拟合度,在其余部分生成大单元,避免网格规模的不必要扩大,从而提高计算效率;同时,网格应使局部曲线光滑和整体疏密过渡自然。在保证上述质量要求的前提下,应尽可能缩短网格生成所用的时间,从而提高整体效率。
生成三角形网格的方法较多,采用商业软件(如SMS[8])、开源软件(如TRIANGLE[9]和EASYMESH[10])等均可快速生成三角形网格,TRIANGLE,GMESH[11],DISTMESH[12]等三角形网格生成方法的一项对比测试[13]表明,针对区域的均匀剖分,随着区域复杂性的提高和网格规模的扩大,TRIANGLE生成网格速度最快,DISTMESH质量表现最优。但随着区域复杂性的提高和网格规模的扩大,各种已有软件及开源库所生成的网格质量问题凸显,如出现钝角三角形、相邻单元面积比过大等。这些问题的解决只能依赖人工手动优化,并且,其局部加密也需要较多的人工控制。利用人工网格调整手段提高网格质量相当耗时,需进行大量的调试和优化,难以提高网格生成效率,开展网格自适应生成研究可有效缓解网格质量和生成效率的矛盾。
针对海洋数值计算中常见的边界不规则、地形多变的复杂区域,目前的网格自适应生成方法缺乏实用性,难以在保证质量和效率的同时,满足实际问题的复杂分辨率要求。基于DISTMESH方法,本研究提出一种普适性的、能精确拟合复杂岸线和地形的三角形网格自适应生成方法,以进行海洋动力学数值模拟空间离散,并将该方法应用于理想潮汐汊道和崇明东滩复杂潮沟系统的网格生成,其中崇明东滩的网格已被用于FVCOM模型流场计算。
1 DISTMESH方法
DISTMESH方法适用于单连通和复连通的离散区域,前者仅包含外边界(指岸线与开边界),后者包含外边界和内边界(如岛屿、水工建筑物边界)。DISTMESH方法通过计算机迭代,一定时间内使网格满足质量和分辨率要求。其网格自适应生成过程如图1所示。每一次迭代过程,包括3个步骤:1)对给定点集,利用Delaunay[14]三角剖分算法进行网格剖分,确定拓扑结构;2)利用距离函数确定区域内的点,即保留上一次迭代后留在区域内的点集;3)确定保留点集的位置及其拓扑结构后,由分辨率函数确定“力-位移”关系,从而将点移动至新位置,也即给定下一次迭代过程的初始点集。其中,距离函数带正、负号,分别与区域外、内相对应,通过正负判断确定保留点集,距离函数的绝对值为平面上各点到边界的最近距离;Delaunay三角剖分算法具有空外接圆和最大化最小角特性,因此,对给定点集,能给出质量最优的拓扑结构;分辨率函数给出模型计算所需网格中各点的分辨率,提出了对目标网格分辨率即单元的大小和分布的要求;“力-位移”关系由分辨率函数确定,由网格现有分辨率与目标分辨率之间存在的差异构造出对三角形边的拉“力”,“力”使边长“变形”,即点发生“位移”。在不断迭代中,“力-位移”关系的建立与求解最终使网格分辨率符合要求。
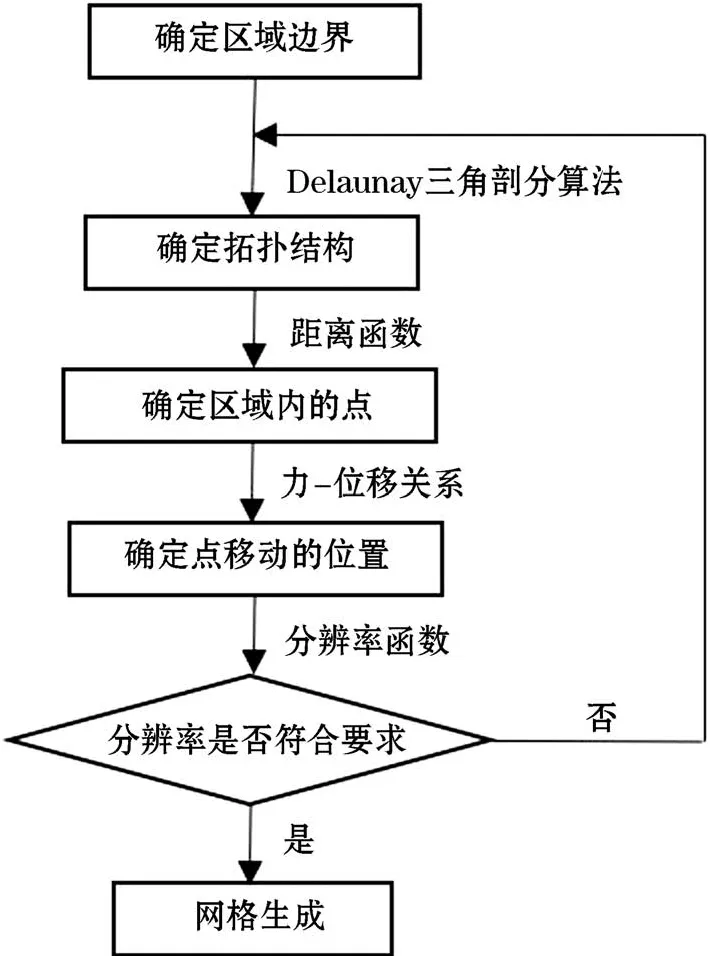
图1 DISTMESH方法网格自适应生成过程Fig.1 The adaptive mesh generating process of DISTMESH
1.1 “力-位移”关系的建立与求解
给定网格点的当前位置和拓扑结构后,需求解网格点移动的新位置。将三角形网格类比为结构力学中的二维桁架结构,三角形边比作桁架杆件,三角形顶点比作桁架节点,力使杆件变形即节点移动。类比仅为使过程便于理解,以下讨论和方程不涉及实际的物理意义和量纲。由节点的当前位置pn和力f(pn),解桁架结构静力平衡方程,得到节点的移动位置:

定义桁架上的力:

式中,l为点处于当前位置pn时的已知现有边长,l0为点处于新位置pn+1时的期望边长;为使点扩散,定义f恒为正;当l接近l0时,f接近0。期望边长计算式:

式中,rb为由分辨率函数给出的现有三角形边中点的目标分辨率;由于f恒为正,因此设置系数z=1.2[12];代表现有边长和目标边长的比例关系。
1.2 分辨率函数及评价指标
实际问题的复杂各异性产生了对目标网格的特定分辨率要求。针对海洋数值计算网格的生成,构建全局分辨率函数和局部加密函数,分别对整个区域和局部区域进行分辨率控制。全局分辨率函数确定网格单元分布的宏观要求,即近岸生成小单元,随离岸距离变大,生成单元扩大;局部加密函数在地形突变处(如存在陆坡、深槽等),修正全局分辨率函数的结果(如分辨率过低),以更准确地描述其复杂的流体动力变化过程,减小模型计算误差、避免模型计算溢出中断。为了确保分辨率函数控制的网格迭代能持续进行至生成网格质量良好,适用于模型计算,提出分辨率函数合理性的评价指标。网格迭代至质量满足要求且继续迭代的质量提升效果不大时,为了合理中止其迭代,提出网格质量评价指标,对网格质量进行综合评估,作为网格迭代的中止判据。
1.2.1 全局分辨率函数
全局分辨率函数中,自变量为网格点与其距离最近的岸线点之间的距离:

式中,(x,y)、(xc,yc)分别为网格点、最近岸线点的位置坐标,dm为距离上限。因变量为网格点分辨率:

1.2.2 局部加密函数
局部加密函数中,自变量为加密区域网格点与其距离最近的加密点之间的距离:

式中,(x,y)、(xr,yr)分别为网格点、最近加密点的位置坐标,d4为加密区域距离上限。因变量为加密区域网格点分辨率:

1.2.3 分辨率函数合理性评价指标
曲线越光滑、疏密过渡越均匀的网格质量越好,但通常其网格规模较大且相邻单元大小更接近,网格迭代和模型计算效率较低;反之,网格规模的减小和相邻单元大小变化较大时,迭代中网格质量将难以提升,模型计算误差由此产生。应综合考虑网格质量和整体效率构建合理的分辨率函数,引入评价指标:

式中,r为分辨率函数设计的目标网格中的分辨率集合,eac指目标网格中相邻三角形面积改变的理论最大值。eac越接近0,目标网格中疏密过渡越均匀。认为eac∈[0,0.5]时,网格迭代持续进行至生成的网格质量良好。但eac越小,整体效率越低,因此,实际应用中,eac值不应过小。
1.2.4 网格质量评价指标
网格质量,包括网格均匀性和单元质量。整个网格的现有分辨率越接近目标分辨率,网格均匀性越好。对均匀性的质量评价,采用三角形外接圆半径与圆心处目标分辨率比值的标准偏差,其值越小,质量越好,认为其值小于0.05时,均匀性质量满足要求。单个三角形的质量:
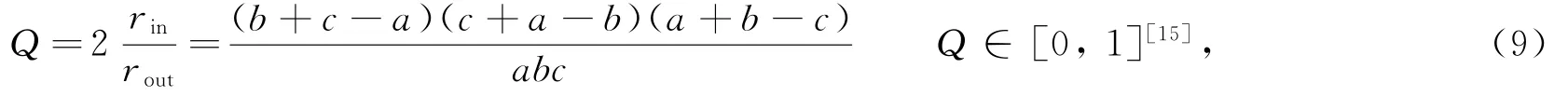
式中,rin为三角形内切圆半径,rout为三角形外接圆半径,a,b,c为三角形边长;Q值越大,质量越好;Q=1,即三角形为等边三角形时,质量最好,Q>0.5时,三角形质量满足要求。
采用以下质量评价指标对网格质量进行综合评估。网格均匀性质量Quni描述整个网格的现有分辨率接近目标分辨率的程度,其值越接近0,质量越好,表达式:
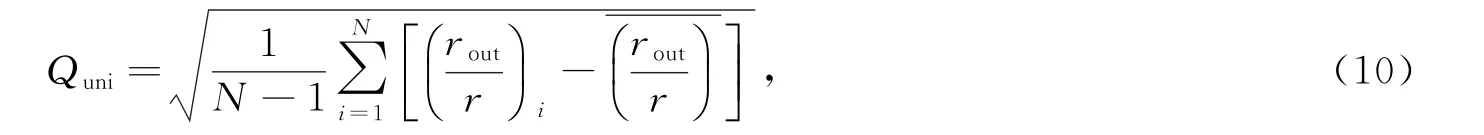
单元平均质量Qmean指网格中所有三角形质量的平均值,其值越接近1,质量越好,表达式:
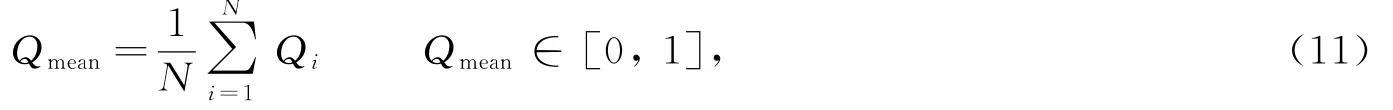
单元最小质量Qmin指网格中质量最差的一个三角形的质量,其值越接近1,质量越好,表达式:
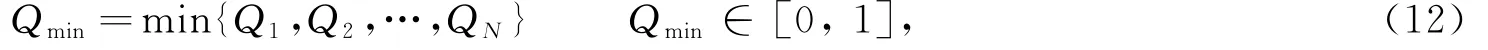
人工调整比例Q05指网格中质量小于0.5即需人工调整的三角形个数占所有三角形总个数的比例,其值越接近0,质量越好,表达式:

式(10)~式(13)中,(rout)i为第i个三角形的外接圆半径,(r)i为第i个三角形的外接圆圆心处的目标分辨率,Qi为第i个三角形的质量,N为网格中所有三角形的总个数,n为网格中需人工调整的三角形个数。
2 应用实例
应用本文方法时,首先参考eac构建出合理的分辨率函数,之后全局分辨率函数对整个区域的分辨率进行宏观控制,需要局部加密时,再结合局部加密函数对局部区域分辨率进行控制,并保证加密区与附近区域分辨率的自然过渡。合理的分辨率函数保证网格迭代的进行,但在网格质量达到良好且提升极其缓慢的情况下,迭代可能仍在进行,因此将网格质量评价指标作为网格中止迭代的判据,选取可用网格和保证整体效率。将本文方法应用于理想潮汐汊道和崇明东滩复杂潮沟系统,其网格生成分别利用了全局分辨率函数和全局分辨率函数、局部加密函数相结合的手段。
2.1 理想潮汐汊道
理想潮汐汊道是近岸地貌动力学数值模拟中的典型理想模型[16],其为长15 km(X方向),宽14 km(Y方向)的矩形区域,北部为开放海域,南部为潟湖,由宽2 km的潮汐通道连通,外边界由北侧开边界和其余岸线边界组成。为探讨本文方法在不同的全局分辨率函数下生成同一区域的网格的情况,在全局分辨率函数合理的前提下,对理想潮汐汊道构建3个参数设置不同的全局分辨率函数type 1,type 2和type 3(表1),其中,预设岸线点分辨率rc均为200 m。
由eac(表1)判断,在3个分辨率函数下,网格迭代均能持续进行至生成的网格质量良好,且网格中疏密过渡均匀程度:type 3>type 2>type 1。网格点与其最近岸线点的实际最大离岸距离约为7 km(图3a),在此范围内,网格点分辨率随离岸距离的3种函数变化关系(图2):随离岸距离的增大,type 1的分辨率迅速增大,之后保持较为平缓的增长;type 2的分辨率始终较为匀速的增长;type 3的分辨率经历了由缓慢增长至较快增长的变化。这代表了空间分布特征各异的3种网格分辨率要求,其单元的大小和分布上的差异表现为:type 1的网格高分辨率区的范围较小,迅速过渡到低分辨率区,过渡区的相邻单元面积变化较快(图3b);type 2的网格相邻单元的面积变化速率较平稳(图3c);type 3的网格高分辨率区的范围较大,相邻单元面积变化缓慢,过渡到低分辨率区后,相邻单元面积变化较快(图3d)。

表1 理想潮汐汊道全局分辨率函数参数和评价Table 1 The parameters and evaluation of global resolution function in ideal tidal inlet
在各函数下迭代生成网格(图4),对同一分辨率函数,迭代10,50,150次的网格分辨率均能体现相似的空间分布特征。type 1函数下,向岸小范围区域内分布着小单元,离岸大范围区域内分布着大单元,两者具有较为明显的分界,分界处迅速由小单元过渡到大单元(图4a,4b,4c);type 2函数下,整个区域中相邻单元面积变化平稳,疏密过渡自然(图4d,4e,4f);type 3函数下,向岸大范围区域内分布着小单元,离岸小范围区域内分布着大单元,疏密过渡较均匀(图4g,4h,4i)。
各函数下的网格迭代随时间的变化(表2、图5)均表现出较为相似的规律。随迭代次数的增大,Qmean不断增大,前期增速迅速,迭代150次时,各函数下的迭代总时间均小于0.25 min,Qmean均大于0.960(表2),之后增速变缓,迭代约400次时均至0.975左右(图5);Q05保持减小趋势,迭代150次时,Q05均小于0.08%(表2),即存在约5个需人工质量调整的三角形,迭代约500次之后均为0(图5);由于迭代随机性的影响,前期Qmin和Quni存在较大波动变化(表2、图5),但总体上,Qmin呈增大趋势,迭代约400次时,其均值0.7左右,Quni呈减小趋势,迭代约400次时,其均值0.02左右(图5);整体网格质量呈升高趋势。
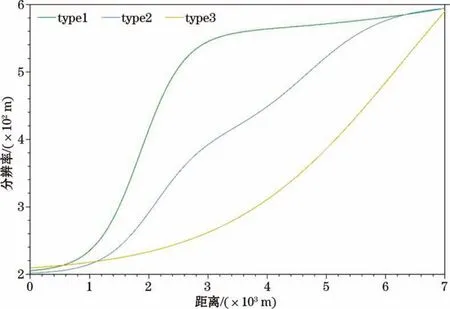
图2 理想潮汐汊道各函数下分辨率随离岸距离变化关系Fig.2 Relationship between resolution and offshore distance under each function in ideal tidal inlet

图3 理想潮汐汊道的距离和3个分辨率函数值Fig.3 Distance and three resolution function values in ideal tidal inlet
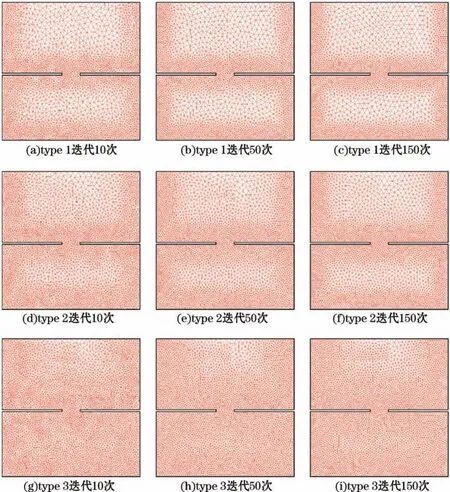
图4 理想潮汐汊道各函数下迭代10,50和150次的网格Fig.4 The meshes after 10,50,and 150 iterations under each function in ideal tidal inlet
在全局分辨率函数合理的前提下,本文方法在不同的全局分辨率函数下生成理想潮汐汊道的网格,其结果显示,eac能作为全局分辨率函数合理性的有效判据;本文方法对不同的分辨率要求均表现出良好的适应性,在相对较短的时间内,获得了质量较好的网格。网格迭代次数相同时,迭代总时间、节点数、单元数和Qmean基本遵循:type 3>type 2>type 1(表2、图5),表明函数相应的网格节点、单元数越多,迭代总时间越长,其网格质量越高;但各函数下Qmean均达到较高水平,其间的差距非常微小。因此使用本文方法时,可根据实际问题,在合理的前提下自由地构建合适的分辨率函数。
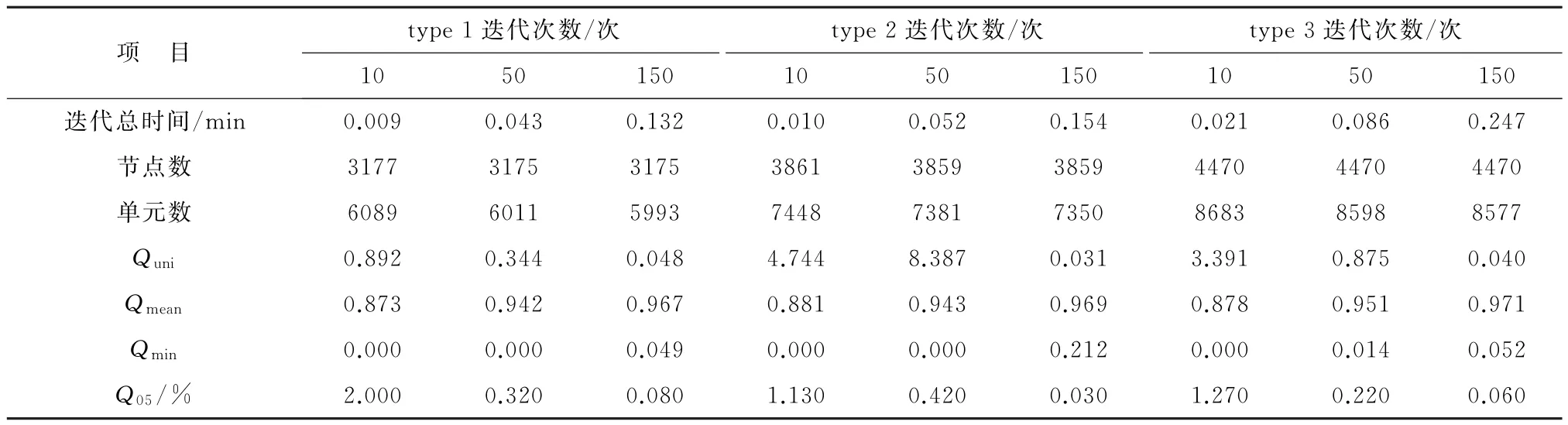
表2 理想潮汐汊道各函数下迭代10,50,150次时的情况Table 2 The evaluation after 10,50,and 150 iterations under each function in ideal tidal inlet

图5 理想潮汐汊道各函数下网格质量随迭代次数变化的过程Fig.5 The mesh quality evolution under each function in ideal tidal inlet
2.2 崇明东滩潮沟系统
潮沟作为潮间带和相邻水域进行物质和能量交换的重要通道,对光滩和盐沼的冲淤过程和地貌形态起着非常重要的控制作用[17],同时对生物迁徙、鱼类洄游等的生态环境产生重要影响。崇明岛位于长江口入海口,崇明东滩位于崇明岛的东端,滩面辽阔,这里发育了数量众多、地形复杂的网络状潮沟(图6c)。崇明东滩数值模拟研究需要精确地拟合其复杂的潮沟地形,大量的网格加密工作由此产生。为探讨本文方法拟合复杂地形生成高分辨率网格的情况,在分辨率函数合理的前提下,对崇明东滩构建全局分辨率函数和局部加密函数,全局分辨率函数参数为dm=30 000,ym=1 000,fr=10,fd=30,s1=3,s2=6,此时eac=0.091。将岸线点分辨率预设在40~500 m范围内,其中,近潮沟岸线的分辨率在40~50 m范围内,潮沟加密点的最高分辨率为6 m,由此取h0=7.5 m。取s=1.14,并取h=0.53h0=3.975 m。在d3=3h=11.925m时,eac=0.488,分辨率变化速率接近限值,保持d3处的分辨率变化速率至d4=170h=675.750 m,此处分辨率接近附近非加密区域分辨率。
由eac判断,网格迭代能有效进行并使生成的网格质量良好,高eac值的局部加密函数要求潮沟与其附近的分辨率差异明显(图7d),对潮沟精确模拟的同时避免了网格规模剧增。网格点与其最近岸线点的实际最大离岸距离约为30 km(图7a)。分辨率函数对单元的大小和分布的控制要求为:整个区域中相邻单元面积变化较平缓,近距高分辨率区的范围非常小,过渡到远距低分辨率区后,相邻单元面积变化加快(图7b);加密区域中,加速增长区范围非常小,迅速过渡到匀速增长区,其过渡处的相邻单元面积变化非常快,并在匀速增长区,保持该面积变化速度(图7c)。
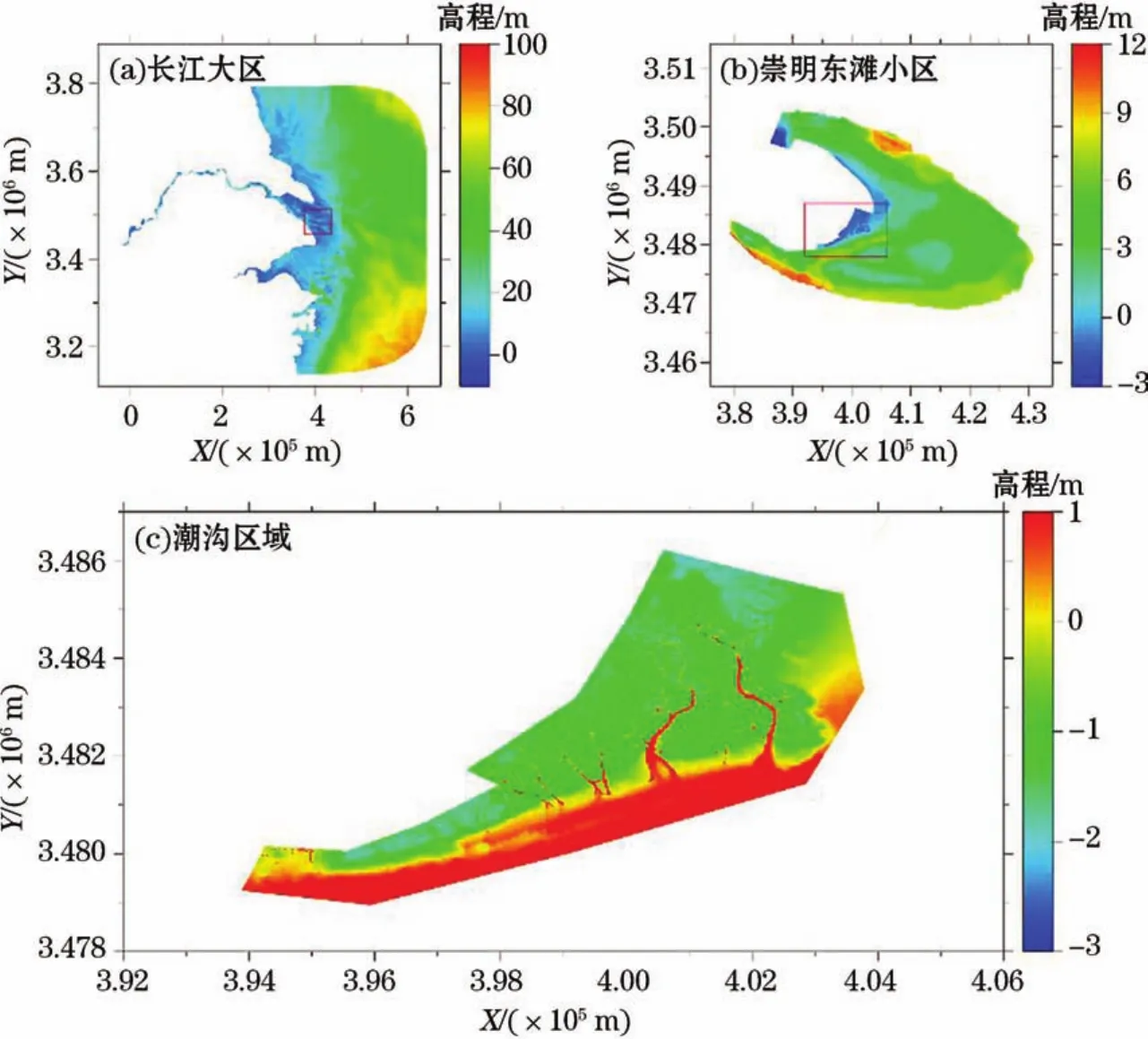
图6 长江、崇明东滩和潮沟区域水深Fig.6 Water depth of the Changjiang River,Chongming Dongtan and tidal creek area
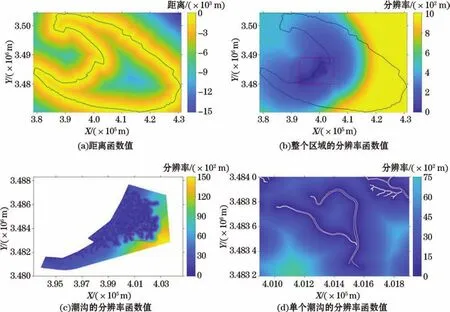
图7 崇明东滩的距离和分辨率函数值Fig.7 Distance and resolution function values in Chongming Dongtan
迭代网格并对网格质量(图8)进行评估。随迭代次数增大,Qmean增大,Q05减小,受迭代随机性的影响,Qmin和Quni有波动变化,但分别具有增大和减小趋势,整体上,网格质量呈增高趋势;迭代105次(迭代总时间127 min)时,Qmean达到了0.960,Qmin接近0;迭代120次(迭代总时间128 min)时,Quni为0.020,此时Qmin仍较小,但Q05接近0;迭代330次(迭代总时间141 min)时,Qmin达到了0.655 6,即不存在需人工调整的三角形。生成的网格(迭代330次)在非加密区域中的相邻单元面积变化平缓,疏密过渡自然(图9a);潮沟能明显的从附近区域中区分出来,潮沟与其附近的疏密过渡自然(图9b,9c)。

图8 崇明东滩网格质量随迭代次数变化的过程Fig.8 The mesh quality evolution under each function in Chongming Dongtan
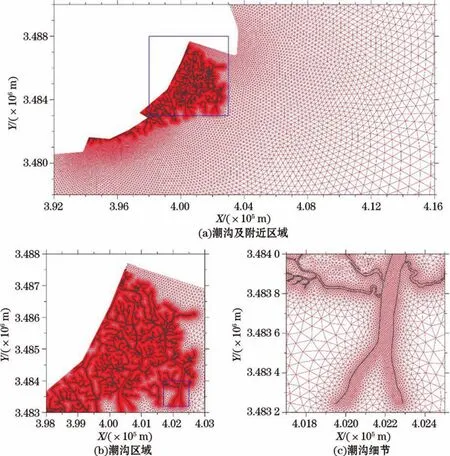
图9 崇明东滩生成网格图Fig.9 The mesh of Chongming Dongtan
崇明东滩数值模拟研究需在长江口大环境中考虑,而潮沟处的高分辨率网格限制了模型时间步长,考虑到模型计算效率,本文采用模型嵌套网格技术,将崇明东滩小区(图6b)模型嵌套于丁平兴等已经发展非常成熟的长江口大区(图6a)模型[18]中。崇明东滩网格迭代至330次(迭代总时间141 min)时不存在需人工调整的三角形,选取该网格进行处理后用于模型计算。计算网格有101 247个节点和201 711个三角形,最高分辨率为7 m。小区模型垂向上采用σ坐标,均匀分11层,采用0.1 s的时间步长,计算22 d。在大区模型中,长江口上界取至潮流界江阴以上200 km左右的大通,钱塘江上界取至老盐仓附近。外海开边界东至124°30′E,北至34°30′N,南至28°30′N。整个区域覆盖了长江各个入海口。网格分辨率在外海陆架海域为0.5~5.0 km,在长江口则精细到200 m左右。更详细的介绍可参考[18]。大区模型垂向上采用σ坐标,均匀分11层,采用1 s的时间步长,计算26 d。流场在外海通过水位作为模型的驱动,采用8个主要分潮M2,S2,K1,O1,N2,K2,P1和Q1。由于水位、流速的响应较快,模型采用冷启动方式,即设置初始场为0。
模型计算流场的最大淹没时刻(图10a)淹没区域可到达离岸150 m处,东滩外的开阔海域呈现显著的落潮流特征。在崇明东滩的潮沟系统(图10b)中,潮沟与滩面这两种地形结构的流场特征存在显著差异,由于水流漫滩距离短,滩面流主要发生在离岸较远的滩面下缘,其流速较小,最大流速约为0.2 m/s;由于滩面水深变化缓慢,流速的空间差异也较小。潮沟处(图10c)的流则主要受到潮沟地形的约束,基本沿着潮沟方向流动,其流速较大,最大流速可达0.5 m/s;潮滩中流速的空间差异较大,主要与水深有关,一般水深越深,流速越大。
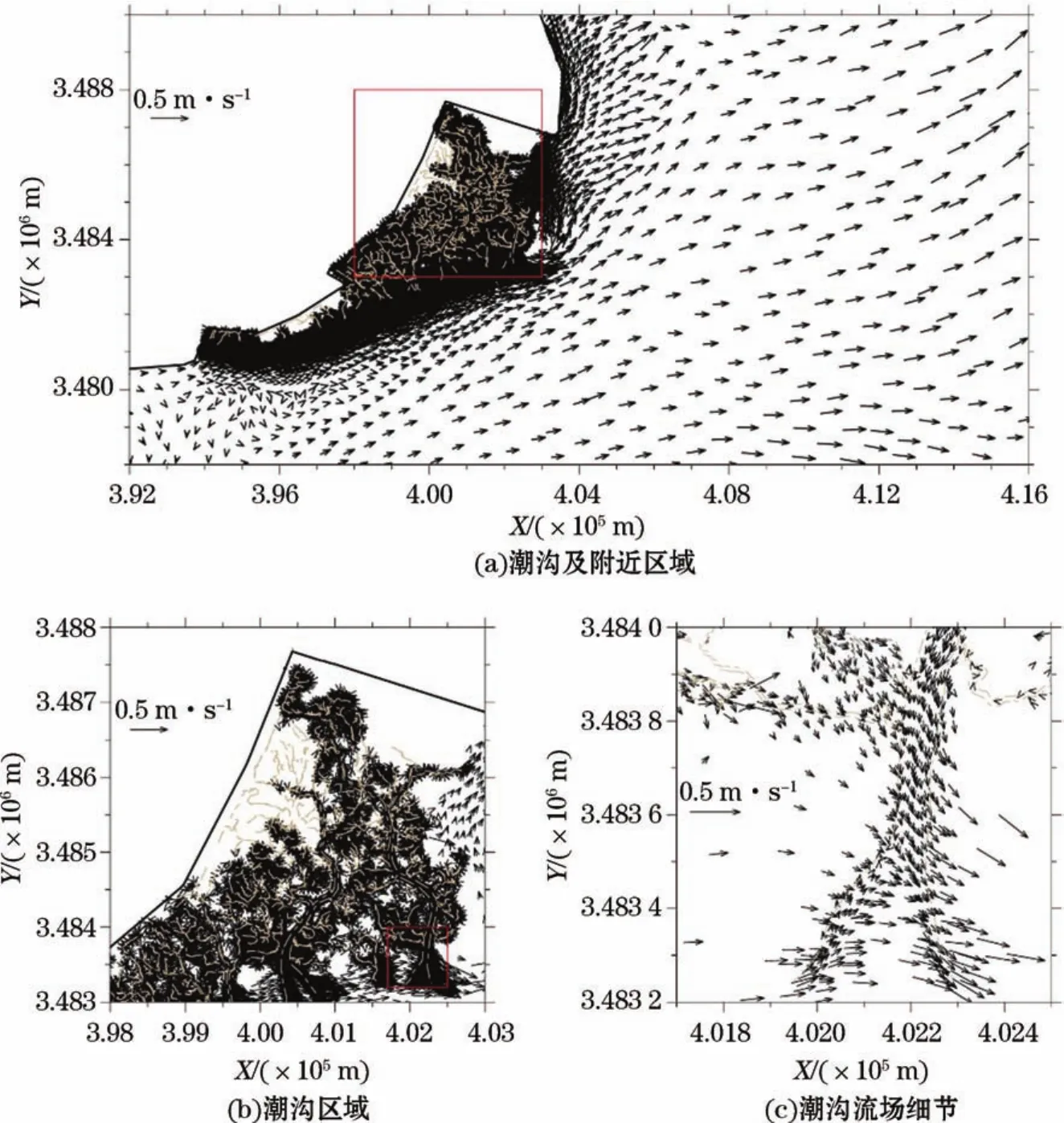
图10 崇明东滩嵌套模型流场Fig.10 The hydrodynamic field in Chongming Dongtan by the nesting model
在分辨率函数合理的前提下,采用本文方法通过全局分辨率函数和局部加密函数相结合的手段,生成崇明东滩复杂潮沟系统的高分辨率网格并进行模型计算,其结果显示,本文方法能在相对较短的时间内完成大量的网格加密工作拟合出复杂的地形,生成网格的分辨率较好地满足了分辨率函数的要求,其网格质量较好。利用质量评价指标能为中止网格迭代选取出计算网格提供可靠参考,保证了迭代效率。由于网格能在流速较大且空间变化显著的潮沟系统中进行加密,而在流速较小且空间变化较小的滩面上采用较少的网格,在保证精确模拟流场的同时,减小了模型网格规模,提高了计算效率。对比其他方法,如在滩面上采用和潮沟相同的空间分辨率,则网格节点数约为220 000,增加2.2倍,这将显著影响模型的计算效率,而将人工网格调整手段运用在极其复杂的潮沟系统中,调整难度较大,需要大量的生成调试过程。在实际复杂问题应用中,本文方法实现了对网格单元的大小和分布的全面精确的控制,有效解决了对网格分辨率特定的控制需求,高效地获得了高精度、高质量的网格。
3 结 语
针对海洋数值模型的空间离散,基于DISTMESH,本研究提出了一种能精确拟合复杂岸线、地形的三角形网格自适应生成方法。该方法保留了DISTMESH方法生成网格质量高、速度快的优点,并将DISTMESH方法中分辨率函数构建为适应于海洋数值模型的全局分辨率函数和局部加密函数,可以对网格生成的空间布局进行多种类型的预先设置,获得了对分辨率全面的控制;eac评价指标确定分辨率函数的合理性,保证迭代的有效开始;多个质量评价指标对网格质量进行评估,合理中止迭代,以提高网格生成效率。将该方法应用于理想和实际案例的网格生成,案例表明,本文方法能满足理想和实际条件下海洋数值模型的空间离散要求,高效地生成高精度、高质量的三角形网格。在实际复杂案例的崇明东滩潮沟系统的应用中,能很好地刻画高复杂度的潮沟网格,并保证了较高的网格质量,从而保证了数值模型的在此复杂边界条件下的可靠计算。

