高中数学线性规划类型及求解策略
■甘肃省天水市第八中学 张满君
一、线性目标函数最值问题及其解答策略分析
求解线性目标函数的最值问题属于考试的基础题型,多出现于选择题和填空题,因为其难度不大,学生较为容易掌握。遇到这类问题时,学生需要根据题目要求,采用图解法一步步求解,这类题型的关键点就是需要学生认真审题,在全面清楚地了解题目要求后再动笔解答,切忌粗心大意。
题目分析:学生具体解答时应该根据题设条件画出数值的可行域,而后将目标函数平移,结合可行域具体分析得出题目要求的最大值。具体可行域如右图1所示:
由图一我们可以非常明了地得出函数z = 3x + 2y 图像在可行域的移动范围,越往右上角移动其数值越大,联立方程组进行求解,可以得出A点的具体坐标为(10,20),代入方程组z = 3x + 2y可以得出其最大值为70。
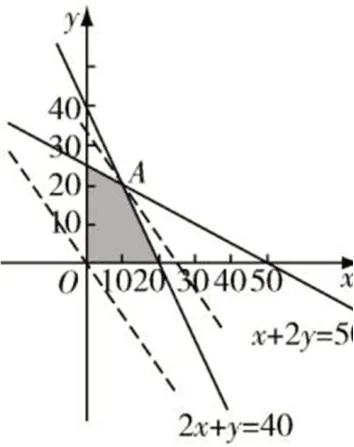
图1
点评:该类型题目基本没有难度,教师应该让学生明确解题的具体步骤,保证看清题目以免因为粗心大意失分。具体解题过程,首先应该正确地画出可行域的范围,准确地计算出直线方程的交点坐标。其次,应该看清题目给出的问题,是求最大值还是最小值,而后根据得出的可行域和极点坐标,保证目标函数图像移动方向的正确性。最后综合分析得出正确答案。
二、非线性目标函数极值问题及其解答策略分析
线性规划中还存在一类求极值题型,其目标函数不是线性函数,难度相比线性目标函数有所增加,采用平移图像的方法无法直接得出结论。但是在解题中仍然需要画出正确的可行域范围,而后学生需要认真观察非线性目标函数,查看其是否是特殊的图像函数,具体如圆、椭圆、抛物线等,而后借助其具体性质进行求解。
题目分析:在实际教学中学生对于求解这类型非线性规划题目存在一定的恐惧心理,因为不像线性函数那样直观明了,教师首先应该根据学生心理将大问题细分,将困难点逐个击破,给学生建立起解题的自信心,只有这样才能在答题时拥有更加清晰的思路。
结合题目我们首先需要根据已知条件画出方程的可行域如图2,但是该方程并不是线性函数,因此需要对目标函数进行简化精减,即,z=x2+y2-10x+ 25=x2+(y- 5)2,由此我们可以看出可行域中的点到点M(0,5)距离平方的最小值,也就是距离最近的点。
接下来,根据题目设定的条件我们画出图2,表示出可行域范围,解答时过点M 做AC 线段的垂直线,MN 长度的平方即为所求的结果,利用点到直线的距离公式,我们可以直接求解出MN的长度的平方值为。所以z=x2+y2- 10x+ 25 在方程组中的最小值为。
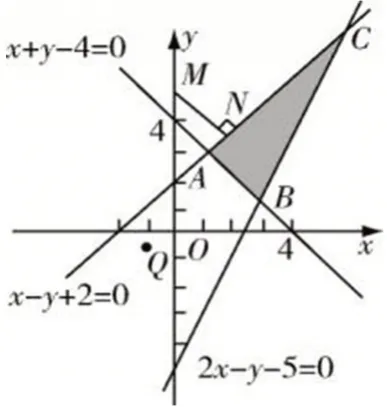
图2
后续点评:解答目标函数如果为非线性函数题型时,除了需要正确精准地画出题目要求的可行域范围外,最为关键的还是需要对目标函数进行巧妙的等式转换,将非线性函数变为已知的函数模型,借助集合意义进行最终求解。
例如目标函数为z=(x-a)2+ (y-b)2的形式,可以看作是可行域中点到点(A,B)的距离,目标函数如果可以转换成为圆方程,应该通过圆心的坐标进行目标转换,进而快速得到答案。总之,学生在面对这类型题目时需要拥有平常心,仔细分析目标函数的形式,尽量地简化成为已知的函数形式,这需要学生在课下自行锻炼和总结。
三、目标函数参数的解答策略分析
线性规划中,目标函数参数问题属于线性规划中逆向思维的题目类型,不同于上面讲到的线性函数和非线性函数,题目灵活性极强,解析难度较大。大部分学生因为没有系统性地理解线性规划题目的核心,面对这类题目时经常不知道如何下手,实际上只要明确目标函数最值一般在可行域边界交点处,而后借助数形结合思想也就不难进行解答。
A.-5 B.1 C.2 D.3
题目分析:解答这类型题目的时候,应该认真分析题目的前置条件,首先将不等式中两个已知的直线方程在坐标中表达出来,而分析ax-y+ 1 ≥0 恒 过 点(0,1),即可以看作是围绕点(0,1)进行旋转的直线,所以,可以根据这些因素做出如图3 所示的图形:
接下来进一步观察题目给出的四个选项,逐个进行分析。当a=-5时,可行域不是封闭的图形,不符合题目条件所以舍去;当a= 1时可以很容易地得出可行域面积为1,保留继续分析;当a= 2 时,可行域的面积为3/2;而当a= 3 时,可行域面积为2。综合分析可以很容易得出只有D选项是最为符合题目要求的,所以正确答案应该是D选项。
题目点评:线性规划中目标函数求解的题目特点是参数难度大,图形复杂,学生如果没能掌握一定的技巧很难进行分析。就上面例题具体分析来看,很多学生不能把握住题目的关键点,也就是ax-y+1≥0恒过点(0,1)这个隐含条件,错失分数。因此解答这类型题目时,学生应该认真分析所有已知条件,先将已知的直线图像表示在平面直角坐标系中,接下来分析具体的直线方程,找出其中隐藏的条件,教师应该针对性地加强这类题目的训练,只有让学生见到更多题目,才能更好地掌握这种题型的解题技巧。
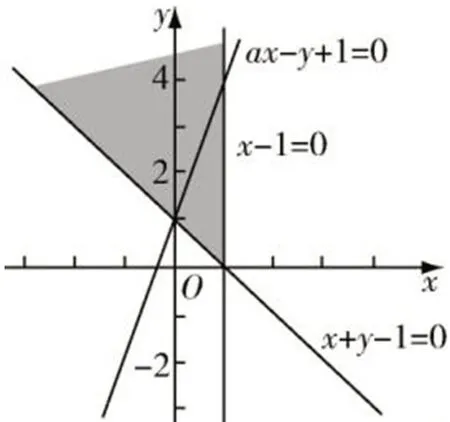
图3
四、结语
综上所述,线性规划是高中数学中较为重要的内容,在考试中因为题型灵活多变,教师需要针对性地总结出其中各类型题目的解题方法,并加强这类题型的练习,将习题量和方法技巧有机结合起来,确保学生真正掌握这一基础知识,以达到快速提升学生线性规划问题的解题效率的最终目的。

