浅谈对数学统一美的探索与运用

钱美芹

[摘  要] 面对新课程改革的挑战，教师需善于挖掘数学本身所特有的美，以数学美去感染和启发学生，让学生从灵感和顿悟中深刻感受到数学之美. 数学美包括多个方面，文章着重结合实例，从数学方法、数学结论、研究过程等方面，谈谈关于数学统一美的一些浅显的见识.

[关键词] 初中数学;数学方法;数学结论;研究过程;统一美

数学具有抽象性的特征，不少学生感受不到数学的美，可以体验到的是它的枯燥无味. 事实上，世界上缺乏的不是美，而是对美的鉴赏. 数学学科不仅孕育着前人对生活中奥秘的探究，还蕴含着人类观察社会的心智和对美的不断追求. 数学的美无处不在，如抽象美、对称美、符号美等，这些多姿多彩的美和谐建构为一个统一体，因此，统一是数学的本质和归宿. 在初中数学教学的实际过程中，运用数学和艺术的眼光观察和发现，充分挖掘其中的數学美，让学生感受到数学的统一美，可以提升学生数学学习的兴趣和学习数学的能力，点燃热爱数学的热情，培养数学学科的核心素养和综合素质，以实现素质教育的有效践行. 本文对挖掘蕴含在数学教与学过程中的统一美这一命题进行分析和探究，结合教学片段谈谈自身的一点拙见.

数学方法的和谐与统一

在浩瀚无边的数学解题中，数学常用的解题方法多种多样，如消元法、图像法、代入法等，它们都是十分重要的解题方法，同时有着广泛的应用性. 当然，对于具体数学问题的解决可以有特殊的解决方法，而对于一类数学问题，则更强调的是通法，通过数学方法的和谐与统一，达到以一法通一类的效果，如，我们可以通过消元法将两元或两元以上的方程问题转化为一元方程问题进行解决. 让学生掌握解决这一类问题的方法，从而找到打开这一类问题大门的“钥匙”，形成一类问题的解题思路，真正做到心中有数地学习. 同时，教师还需关注到一题多解的训练，以此激发学生发现解题思路中的统一性，不仅有助于探寻到多个不同的解题思路和方法，感受到数学方法的和谐与统一，还有利于学生的思维从发散向着创新推进，富有个性地解决数学问题.

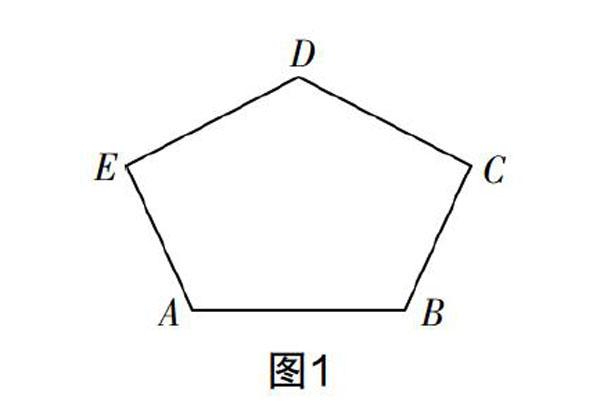
案例1？摇 如图1，请试着计算五边形ABCDE的内角和.

学生经过思考，形成了以下多种多样的解法：

方法1：如图2所示，可将这个五边形划分为三个三角形，进而计算出内角和为540°;

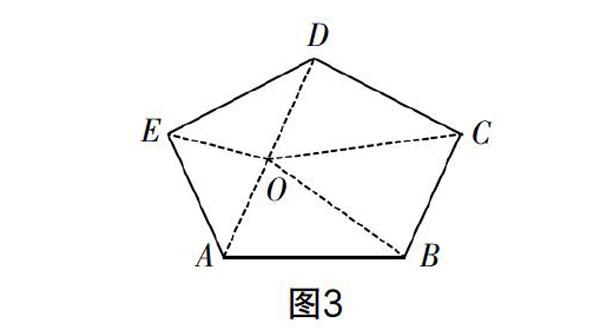
方法2：如图3所示，在该五边形内任意取一点O，即可将五边形划分为五个三角形，进一步求和即可得出内角和为540°;

方法3：如图4所示，在该五边形的一条边AB上取任意的一点P，即可将其划分为四个三角形，进一步求和即可得出内角和为540°.

通过以上3种解法，学生进一步归纳和概括得出以下统一特征：①均转化为三角形的内角和进一步求解;②均通过顶点与其他点的连接来解决. 通过以上的概括，教师还可以提出以下高质量的问题：若这一任意一点在该五边形外侧，那是否一样可以求出该五边形的内角和呢？通过高阶思维的引领，使其成为培养学生理性精神和创新能力的催化剂，让学生在深度学习中感受数学方法的统一美.

评注  在解决一道数学问题时，往往有着各种各样的数学方法，这些方法之间又都具有一定的统一性. 上例中的一题多解就是方法统一性与多样性的体现，让学生通过探究得到解决问题的多个路径，并对具体方法进行概括和总结，帮助学生真正理解问题本质，实现思维的锻炼和深化，感受数学的统一美，这样的思维过程远比教师直接灌输而获得的能力更重要.

数学结论的和谐与统一

和谐与统一是数学美的最高境界. 若将数学比作一座金碧辉煌的宫殿，那统一美就是这座宫殿的建筑特色，不管是从其局部还是从整体入手观察，都可以感受到它的浑然一体和相互呼应的美感. 在自然科学中，人们一直都未停止过对统一结论的追求，这对于数学学科来说更是显而易见的. 结论的统一是数学家们从未放弃的追求，数学中的公式和定理皆是一类问题的统一结论，更是对其高度的总结和概括，如，在数的概念中，从自然数延伸到无理数，再生长到复数，数的概念的研究不断扩充，不断延伸，从而进行统一的概念性规划，实现数学的统一美.

案例2？摇 从定理“平行四边形的对角线相互平行”延展谈起.

问题1：图5中共有多少条不同的线段？

问题2：图6中一共有多少个小于180°的不同角？

问题3：足球场上一共有n支足球队在比赛，采用的是单循环制，那么共需比赛的场数是多少？

问题4：一大型聚会共有n人参加，见面后每两个人都需握手一次，那么一共需握手的次数是多少？

......

评注  观察以上问题，不难看出这些问题的背景皆不相同，内容也毫无关联，但均有着惊人的统一——结论的统一，也就是■. 课堂教学是师生交流和生生互动的场所，若是教师能有意识地挖掘，在教学中灵活巧妙地安排好每一个教学环节，指导好学生的归纳和理解，就能让学生在数学理解的层面上感受到数学的魅力，真正意义上感受到美的熏陶，进而感受到数学带来的趣味性和美的享受，让学生在美的熏陶中学好数学.

研究过程的和谐与统一

数学的统一美不仅强调数学方法和数学结论的统一，在数学教学中还应着力剖析数学研究过程的和谐与统一，如一些几何图形的研究过程都需经历“定义—性质—识别—应用”的研究阶段. 解题过程中的统一美从未停止过，在理解中感受解题过程的统一性，可以进一步优化认知结构，提升关键性能力.

案例3  如图7，已知平面直角坐标系xOy中，点A（10，0）. 以OA为直径，在第一象限内作半圆，且点B为该半圆的圆周上的一动点，连接OB，AB，并延长AB至点D，使得DB=AB. 再过点D作x轴的垂线，与x轴和直线OB分别交于点E，F，E为垂足，连接CF.

（1）当∠AOB=30°时，试求出弧AB的长度.

（2）当DE=8时，试求出线段EF的长.

（3）随着点B的不断运动，是否存在以点E，C，F为顶点的三角形相似于△AOB？若存在，求出点E的坐标;若不存在，请阐明原因.

解：（1）略

（2）①如图8，当交点E在A，C之间时，连接OD.

因为DB=AB，OB⊥AD，所以OA=OD=10.

又DE=8，所以OE=6，所以AE=4.

又△FOE～△ADE，所以EF ∶ AE=OE ∶ DE，从而解得EF=3.

②如图9，当交点E在点O左侧时，连接OD.

因为DB=AB，OB⊥AD，所以OA=OD=10.

又DE=8，所以OE=6，所以AE=16.

又△FOE～△ADE，所以EF ∶ AE=OE ∶ DE，从而解得EF=12.

（3）略.

评注  从上述解题过程可以看出，尽管第（2）问中的两种情形在图形和结论上都表现出较大的差异性，但在解题过程中却能做到基本统一，让学生在感受统一性的同时，实现数学思维的突破.

伽利略曾说过：数学总是美的，数学是美的科学. 数学的统一美可以消除学生枯燥乏味的成见，让学生感受到数学是一个五彩斑斓的美的世界. 在初中数学教学中，数学的统一美不仅表现在以上三个方面，而且存在于教学的多个环节之中，需要我们广大数学教师融合艺术与数学进行挖掘与提炼，建构学生崇尚真理的情感与精神力量，使其感受到数学的无穷魅力，由此才能更好地发挥数学教育的价值.