群智感知网络中基于社会关系的社区发现算法

龙 浩 ，张书奎 ，张 力

1.苏州大学 计算机科学与技术学院，江苏 苏州 215006

2.徐州工业职业技术学院 信息与电气工程学院，江苏 徐州 221002

3.江苏省现代企业信息化应用支撑软件工程技术研发中心，江苏 苏州 215104

1 引言

随着嵌入了大量传感器的移动智能设备迅速普及，移动群智感知应用得到了广泛的应用，移动用户携带移动终端设备能够在不同的位置监测到复杂的数据信息（比如：噪音、天气、大气、交通）。目前开发了大量的移动群智感知应用，包括医疗健康、环境监测、交通状况等方面[1-2]。移动群智感知应用的任务一般需要根据用户的位置信息和行为特征进行分配，因此统计并分析用户的历史记录，挖掘用户的行为模式是感知任务分配的重要前提。从社交网络可以看出，现实中用户内部社会属性通过凝聚和细化形成社区结构，即同一社区中的用户彼此紧密联系，彼此之间建立了一定的信任关系，因此社会关系比较固定。相反，不同社区的用户社会属性包括兴趣爱好、活动范围、交往联系等都相差很大。社区发现的目标是根据用户特定的行为模式和社会属性划分网络，并探索网络潜在关系模型，提炼社区成员具有的共同特性。群智感知应用利用用户的移动和交互完成感知任务，现实中执行感知任务的人具有一定的社会关系，它是用户生活工作所具备的基本社会属性，根据行为规则和交互频率，可以将不同的用户划分为不同的社区。群智感知应用依靠历史记录信息进行聚类发掘，识别网络固有的社区结构，感知平台可以根据不同社区的特征值将对应的感知任务分发给该社区的用户执行，提高任务分发效率和任务执行的正确性[3]。因此，通过社区分配感知任务是群智感知应用研究的重要步骤，目前社区划分方法有基于用户社会角色的属性社区划分[4]，基于用户地理位置的位置社区划分[5]等。社区结构的发现对于提升感知任务用户群的匹配度，节约感知任务执行时间，提高感知数据质量都具有十分重要作用。

2 相关工作

在群智感知研究中，任务分配是群智感知应用研究的重要环节，而任务分配主要通过挖掘用户特征提升任务分配用户群的匹配度，从而提升感知数据质量。基于社区发现的感知任务分配算法是目前研究的热点方向。在群智感知应用中，移动用户的交互构成了一种典型的动态复杂网络，用户之间的社会关系为感知任务的分配和执行提供了强有力的支持，相互之间内在的社会关系形成了紧密相联的社区[6-7]。赵卫绩等人[8]提出一种基于加权共同邻居相似度的局部社区发现算法，通过计算节点间的相似度指标发现局部社区。然而该方法社区发现的特征因子过于单一，其准确性有待进一步提高。赵健等人[9]在群智感知服务中提出了一种面向有向加权网络的社区发现算法，通过计算节点间的最优路径，相似度等合理划分社区。然而该方法中并没有考虑节点的动态性，也没有考虑特征因子的权重分配。Chen等人[10]提出了一种基于用户交互行为的加权动态在线社交网络社区检测方法，研究了在线社交网络中用户的交互行为，通过描述个体之间的亲密度以及用户模块密度进行社区探测。Ibrahim等人[11]提出了一种基于网络概念格结构的概念兴趣度社区检测算法，首先探测所有的小团体和团体之间的关联，然后使用稳定性指数去除社区之间的关联，合并相关的邻近小团体。然而该方法中基于兴趣度的小团体探测，未考虑到节点的位置因素，社区合并方法时间复杂度较高，不适合实时性要求高的群智感知应用。针对群智感知社区发现算法的问题，提出了一种基于社会关系的社区发现算法，首先给出了用户之间边权重定义方式，并基于此定义选择权重最大的边生成最优生成树作为初始社区；进而计算未划入社区的其他用户与初始社区的合并因子，形成明显的社区结构；最后，将重叠率比较高的用户划分到对应社区，从而得到最终的社区发现结果。

3 社区发现算法

通过量化节点之间的社会关系，将节点聚类成具有真实社会关系的社区网络。针对网络中的各个节点，首先构造出节点的最优生成树，形成初始社区，然后计算相邻节点的合并因子，通过合并因子来判断节点是否处于同一社区，完成最优生成树的合并，形成明显的社区结构，最后用社区调整因子来检验社区划分的紧密度，衡量社区结构划分效果，并进行适当调整，从而完成网络中社区的最佳划分。具体社区划分过程如图1所示。

图1 社区划分过程示意图

3.1 最优生成树

假设G(V,E)是无向加权网络，节点集合V包含了n个节点，边集合E包含了e条边，每一条边有两个顶点(vi,vj)在V中。社区划分的目标就是要将G划分成k个社区：U={u1,u2,…,uk}，其中ui≠ui∩uj=

定义1从网络G中的节点vi开始，直到包含所有的节点集合V截止，以任意节点vi为开始的最优生成树路径值的计算通过以下公式得出：

其中，j,x,y为中间相邻节点，最优生成树的构造是通过所有相邻节点的权值φ最大值求和[12]，φ(i,j)为计算两相邻节点的权重值，称作两节点的社会关系值，具体计算办法如下：

式（2）中Γ(vi)表示节点i的邻居集。

最优生成树的建立过程类似最小生成树算法Prim的原理，是以网络中的任意节点vi∈V作为根节点，并每条边的权重按降序排序，每次挑选一个权重最大的边，使用Union-Find算法检查将其加入到最优生成树时，是否会形成环，重复该步骤直到最优生成树中有V-1条边。网络G(V,E)的一棵最优生成树设为OST(V′,E′),V′=V,|V′|=|V|,E′⊂E,E′=V-1 。在最优生成树OST中选择边权值最大的V-1条边，设为集合E′，然后将OST中在集合E′中的边移除，得到了V-1个相互独立的部分，把它称为初始社区，记为U={u1,u2,…,uh},h=V-1。

3.2 节点合并

目前大多数社区划分算法通过计算节点间的相似度来实现，然而由于聚类方法的不同，节点间相似度的定义在不同的算法中各不相同。考虑到群智感知的应用场景，划分的最终目标是根据节点区域来分发不同的任务，因此社区的划分主要根据节点间的社会关系和位置聚类形成的，本文社区划分方法提出节点合并因子的定义，将节点的节点合并因子定义为节点间社会关联度和位置特征，通过节点合并因子来实现初始社区的合并，形成明显的社区结构。本文将节点合并因子量化为两个值：第一个值是根据节点历史相遇记录引入一个社会压力度量值（Social Pressure Metric，SPM）来探测节点间连接质量πi,j[13]，衡量节点间的社会关联度；第二个值是通过GPS获取移动用户的位置特征（经度和纬度）并采用欧氏距离公式计算两节点的距离作为节点位置特征。社区的合并需要根据节点间的联系紧密度来计算，一般来说两个节点之间属于朋友和邻居关系，可以认为这两个节点联系紧密，具有较高的连接质量。然而，存在朋友关系的节点对可能会处在距离比较远的两个区域，根据感知任务区域划分的特点，这两个节点不能划分到同一社区，因此，需要考虑采用节点的位置特征值来进行校验。下面具体对节点合并因子进行定义。

定义2节点合并因子包括节点间社会关联度和位置特征，节点之间的社会关联度定义为SPM的倒数。节点间的位置特征值由欧氏距离公式[14]计算获得。

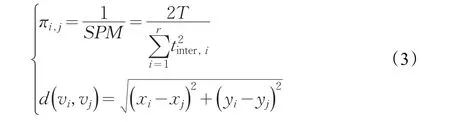
其中，T为任务执行周期，tinter为节点相遇间隔时间，r为间隔次数，(xi,yi)为节点i的坐标位置。下面介绍具体合并过程。首先计算初始社区中任意两个社区节点对的社会关联度是否大于阈值ψ，如果大于阈值则计算节点间距离是否小于阈值ε，两个条件都满足则建立两个节点的连接，并将两个节点保存到同一社区ui中，直到所有的社区不能再合并为止，形成的{u1,u2,…,uk}即为合并的社区划分。为了降低节点间节点合并因子的计算和判别，考虑如果两个初始社区中任意节点对之间的社会关联度和距离满足阈值，则将两个社区进行合并。

在社区合并过程中，可能会有一些顾虑。首先，假设节点在一定时间内处于有限的迁移场景中。事实上，节点的活动具有一定的特点，在某个时间段，节点的活动范围一般情况下并不会超出所属社区的范围，尤其在接收感知任务期间。第二个问题是有部分节点移动到别的区域或者有新的节点加入。首先可以根据移动节点的历史信息计算是否可以加入对应社区，如果不满足条件，计算移动节点或新节点与邻居节点的距离，如果小于阈值ε则加入邻居节点社区。第三个问题是在某个时间阶段后，大部分节点进行了移动，社区需要进行重新划分。社区的动态变化特征超出了本文的范围，将其作为未来的工作。

3.3 社区调整

考虑到在实际网络中社区结构是自然形成的，社区内部各个节点的连接比社区间节点的连接要紧密得多，然而这只是一个定性的指标。本文提出了社区调整因子的概念，从定量角度来衡量社区划分的质量，对一些社区间的重叠节点做进一步优化，重叠节点即节点i∈uk，同时i∈uj，优化的目的是要将重叠节点i划分到对应社区中。

定义3社区调整因子通过任意节点i的度来衡量社区划分质量。如果∀i∈uk，社区uk应满足(uk)≥(uk)。

其中(uk)表示节点i与社区uk内中其他节点连接边的条数，(uk)表示节点i与社区uk外其他节点连接的边数。如果社区内任意节点与社区外部节点的连接，比它与社区内部节点的连接更紧密，那么就将该节点调节到对应社区。

3.4 社区划分算法

社区划分算法实现过程主要包括三个步骤：（1）根据公式（2）计算各节点的权值，构造一棵最优生成树，然后删除最优生成树中集合E*中的边，将最优生成树分裂成h个初始社区；（2）根据公式（3）计算相邻节点对的节点合并因子，判断节点合并因子是否满足阈值，将初始社区进行合并，重复该步骤，直到所有的初始社区全部合并为止；（3）判断社区调整因子指标，衡量社区划分质量，调节不满足定义3的相关节点到对应社区。

算法1社区划分算法具体描述如下：

输入：网络G(V,E)，相邻节点合并因子阈值ψandε。

输出：划分完整的社区结构集合U={u1,u2,…,uk}。

1.for each node pair(vi,vj)inV

2. Calculatedφ(i,j)by（2）

3.end for

4.Build OSTT

5.RemovingV-1the edges of highest weight fromE′

6. ProducedV-1communitiesU={u1,u2,…,uh}

7.for each community pair(ui,uj)inU

8. if ∀πi,j>ψandd(vi,vj)<εthen

9. mergeuiandujtoui

10. deleteui

11. end if

12.if all communities cannot merge then

13. break

14. end if

15.end for

16.Get merged communitiesU={u1,u2,…,uk}

17.whileifrom 1 tokdo

18. if

19. continue

20. else

21.adjustiinto the corresponding community

22. end if

23.end

24.returnU={u1,u2,…,uk}

算法描述中节点对的社会关联度判断阈值ψ需要根据任务的时间周期来决定。连接距离判定阈值ε根据感知任务区域的半径（单位：m）一般ε∈（50，250）[15]。算法复杂度分析，首先最优生成树的建立类似如Prim算法，其运行时间是O(|E|+|V|lb|V|)=O(m+nlbn)，然后将初始社区合并时间复杂度为O(n2)，社区调整因子检验时间复杂度为k。因此整个社区划分算法的时间复杂度为O(n2+nlbn+n)。

4 算法性能分析

为了验证社区发现算法的划分效果，通过计算机合成网络和真实世界网络分别进行社区发现实验。实验在一台配置了Inter Core i7-5557U CPU 3.10 GHz和8 GB内存的笔记本上进行，操作系统为 Windows 8.1，使用JAVA语言在myclipse编程实现。本文算法与常见典型社区发现算法进行了对比实验，采用的对比算法主要包括：基准社区发现算法（CNM）[16]，基于增量密度的社区检测算法（IncOrder）[16]，基于最优生成树和模块的社区划分算法（CDOSTM）[12]。采用下面三种评价方法评价社区发现算法的效果，验证社区结构的有效性、合理性和正确性。所有实验结果至少1 000轮后取平均值。

采用归一化互信息[17］（Normalized Mutual Information，NMI）来度量通过算法划分社区和真实社区之间的差异程度。设真实社区结构划分为G={g1,g2,…,gn}，算法划分的社区结构为C={u1,u2,…,uk}。社区划分的归一化互信息表示为：

其中，Nij=gn⋂uk表示原始社区和算法划分社区共同拥有的节点数，Ni.表示社区gn的节点数，N.j表示社区uk的节点数，算法划分的社区与原始社区完全一致，则NMI=1，当完全不一致时，NMI=0。

采用社区模块度评价函数Q[18-19]来评价社区划分的质量，函数定义为社区内实际连接数目与随机条件下期望连接数之差，具体函数公式如下：

公式中，n表示划分社区的数量，E表示节点连接的总边数，Ec表示社区中节点间连接的总边数，DC表示划分社区后节点间的权重之和。由公式（5）可以知道，当网络具有明显的社区结构时，Q接近为1，当网络中社区结构不明显时，Q接近于0。在实际社区划分算法中Q通常在[0.3，0.7]之间，通常认为Q>0.3时算法划分具有较好的社区结构。

社区划分结果的正确性通过调整兰德系数ARI（Adjusted Rand Index）[20]指标进行评价，ARI的定义如下：

数据集的两个社区划分设为A和B，其中A有KA个簇，B有KB个簇，Ni表示划分A中第i个簇中节点的数量，Nj表示划分B中的第j个簇中节点的数量，Nij表示在划分A的第i个簇中的节点同时也在划分B的第j个簇中节点的数量。ARI可以用来评价社区发现算法的效率和划分社区与真实社区的吻合程度。从ARI的定义可以看到，ARI(A,B)越接近于1，表示社区之间的关系越独立，如果ARI(A,B)越接近于0，则表示社区之间的关系越紧密。

首先进行合成网络实验，采用LFR作为测试网络，LFR是目前社区发现算法实验的基准测试网络，是最为常用的模拟数据集，它模拟了真实网络中节点度和社区大小的无标度性质，能够用来评价算法发现社区的质量。通过设置不同的混合参数，能够生成不同类型的模拟网络，节点间的权重随机生成。实验中LFR基准网络设置参数如表1所示。

表1 LFR基准测试网络参数设置

在表1中列出a和b两种综合网络的参数，其中a代表网络划分的社区数相对较少，b代表网络划分的社区数相对较多。n表示节点的总数；m表示节点之间边的总数；k表示网络中节点间平均权重；minc表示最小社区包含的节点的数量；maxc表示最大社区包含的节点的数量；mu表示节点与社区外部连接的概率，定义为重叠参数。LFR基准网络中，mu的值越大，社区发现的难度就越大。因此对每个重叠参数mu值，在实验过程中随机生成20个模拟网络，对应四个算法的NMI，ARI值分别为在这20个模拟网络上运行得到它们的平均值。算法对比如图2、图3所示。

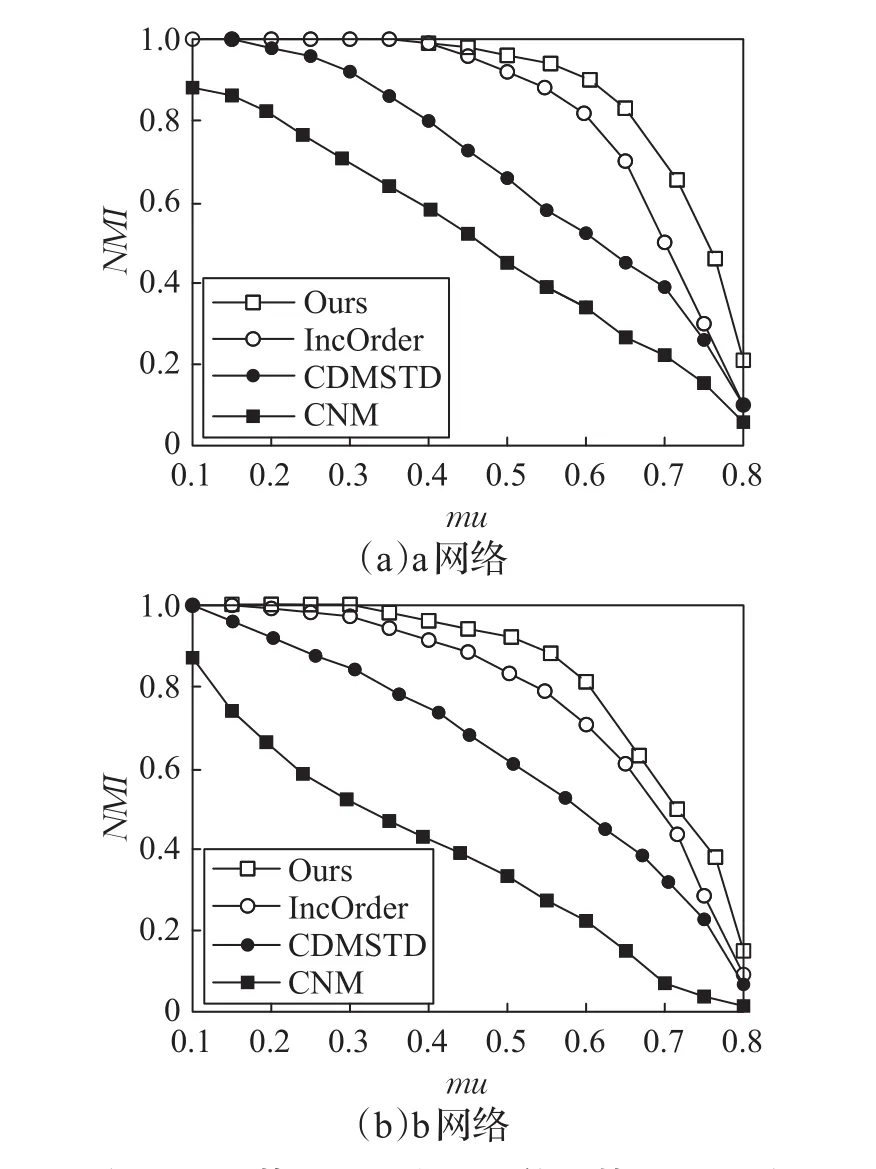
图2 LFR基准网络中NMI值的算法对比图

从图2（a）和图3（a）中可以观察到本文算法相比其他三种算法具有较优的社区检测结果。尤其当mu<0.4时，本文算法的NMI和ARI值接近于1，此时的网络社区结构比较清晰，能够很准确地检测到网络中的社区结构，得到的划分结果几乎完全接近正确的划分结果，而检测结果最差的是基准算法CNM。当0.4

图3 LFR基准网络中ARI值的算法对比图

真实网络实验中，选择三个数据集来验证算法的有效性，包括Football、Amazon、Gowalla。其中Football有115个节点，613条边，划分成12个社区，节点关系比较清晰，网络相对较简单。Amazon是一个大型网络，每个商品都有自己的属性，根据商品的不同属性进行分类，能更好地测试算法性能的伸缩性。Gowalla数据集是一个基于地点的社交网络，用户用签到的方式通过公共API分享他的位置，通过不定时的签到能够获得用户的位置信息，为分析人的行为特征提供了重要的依据，Gowalla数据集非常适合对本文算法进行性能检验。三种真实网络由简单到复杂，网络节点有各自的特点，因此更能检验算法的性能和效果。采用三种评价标准来进行算法的比较，具体结果如表2所示。

表2 不同数据集的具体算法比较

从表2中可以看出本文算法相比其他三种算法，无论是简单网络还是复杂网络的社区划分都能取得很好的效果，尤其对Gowalla数据集的社区划分，其他三个算法的效果与本文的算法相差较大，由于Gowalla数据集中用户是动态移动的，用户移动到什么地方，怎样移动，用户的移动和社会关系是如何关联的，都是随时变化的，而本文算法恰好是基于移动节点的行为特征来进行社区的划分，因此能取得很好的效果。

5 结束语

社会关系是目前群智感知应用中任务分发的研究难点，涉及记录的时间、空间和行为等多种特征因子。本文首先借助社会网络理论，综合考虑影响社会关系的多维因素，提取移动节点间的最优生成树、节点合并因子、社区调整因子作为社会关系量化的特征因子，抽象和识别出节点的行为模式，将用户合理划分成不同的社区。最后，通过实验验证本文所提社区发现算法具有较好的动态适应性、有效性和准确性。后续工作将主要针对社区划分的动态性，以及基于社区划分的移动群智感知任务分配算法进行研究。