深度非负矩阵分解的链路预测方法研究

蔡 菲，张 鑫，牟晓慧，陈 杰，蔡 珣

1.山东建筑大学 测绘地理信息学院，济南 250101

2.山东大学 计算机科学与技术学院，济南 250101

1 引言

链路预测是近年来复杂网络中的研究热点之一，它能够帮助探索和理解复杂网络的演化机制。目前，复杂网络中，现有链路预测方法可分为两大类。第一类基于节点相似性的方法，认为两个节点之间相似性越大，它们之间存在链接的可能性就越大[1-3]。这类方法均依赖于网络拓扑结构，虽比传统链路预测方法提高了预测精度，但在稀疏网络中预测能力仍然有限。第二类方法是基于统计分析和概率论，如概率关系模型[4]、层次结构模型[5]和随机块模型[6]。这些方法通常假设网络有一个已知的结构，通过构建模型并使用统计方法估计模型参数，进而计算每个没有观测到的节点之间连边的形成概率。基于概率和统计的方法在网络分析中有许多优点，但是参数学习和推理却使计算复杂性大大增加，使得基于概率和统计的方法在应用领域受到很大局限。

目前的链路预测研究也越来越关注从网络节点的隐特征信息出发构建链路预测方法。非负矩阵分解方法能够提取隐特征，其本身也是一种降维方法，因此，非负矩阵分解也成为了隐特征模型的实现基础[7-8]，例如文献[9]提出了一种带有图正则非负矩阵分解的链路预测方法。文献[10]提出了将图通信性和非负矩阵分解相结合进行时序网络链路预测并取得了良好的预测效果。但现有的非负矩阵分解方法在稀疏网络中链路预测能力仍然有限。

在矩阵分解中，系数矩阵和原始数据矩阵之间的映射包含了相当的非线性结构信息[11]。因此，本文针对非负矩阵分解直接将原始网络映射到隐空间中，不能充分挖掘复杂网络的深层隐结构信息，导致在稀疏网络中预测能力有限，提出一种新颖的融合网络多层结构信息的深度非负矩阵分解预测方法（Deep NMF，DNMF）。首先通过对系数矩阵多次分解，得到一组基矩阵和一个系数矩阵相乘，进而构建深度隐特征模型的目标函数。然后，采用两阶段法去调整训练参数，即在预训练阶段通过逐层分解作为预分解结果，在微调阶段整体微调训练参数，从而实现逐层学习策略。逐层学习策略可以使深度非负矩阵分解不同层级间的参数进行“剖分”式学习，可以大大节省计算存储资源和时间，提高方法的泛化性能。因此，该方法可以在保证真实网络的深层隐结构信息表达的同时使其获得更加丰富和全面的网络结构信息，从而进一步提高链路预测的预测精度。

2 问题描述

网络由节点和边组成，给定一个无向无权网络G=(V,E)，V和E分别表示网络中的节点和边的集合。N=|V|和M=|E|分别代表网络的节点和边的数量。A代表网络的邻接矩阵，如果节点i和节点j之间有连边，则Aij=Aji=1，如果节点i和节点j之间没有连边，则Aij=Aji=0。

针对链路预测问题，将网络的边划分为训练集和测试集，表示为Etrain和Etest。显然Etrain⋃Etest=E并且Etrain⋂Etest=。使用Atrain和 Atest分别表示训练集的邻接矩阵和测试集的邻接矩阵。邻接矩阵中元素值为1或0，并且 Atrain+Atest=A。L=|Etest|是测试集中的边数。因此，训练集边的数量为|Etrain|=M-L。在训练集之外，将网络中的所有可能边作为候选集。从训练集Etrain中学习模型，然后计算候选集中节点间每个可能边的分数值，将分数值从大到小排列，并根据不同评价指标对测试集Etest的结果进行验证。

3 基于深度非负矩阵分解的链路预测

3.1 非负矩阵分解

非负矩阵分解（NMF）是一种矩阵分解算法，它是一种使数据的隐结构更加显式化和减小其维数的方法。因此，它可以进一步应用于链路预测[12]。给定一个网络邻接矩阵A∈RN×N，可近似为W∈RN×K和H∈RK×N。

为了量化近似的质量，用欧氏距离平方的代价函数可以写成如下：

其中，W和H分别表示基矩阵和系数矩阵。根据文献[13]提出的迭代更新算法，该算法最小化目标函数如下：

3.2 深度非负矩阵分解

在非负矩阵分解的基础上，本文提出了一种深度非负矩阵分解的算法（Deep Non-negative Matrix Factorization，DNMF）。

通过对NMF分解的系数矩阵H进行m次分解，从而进一步融合了网络的多层结构信息，其分解示意图如图1所示。

图1 NMF与深度NMF的对比示意图

DNMF通过对系数矩阵的多重分解形成多层网络结构学习模型H的分解步骤如下：

步骤1分解网络邻接矩阵A≈W1H1，W1∈RN×k1和 H1∈Rk1×N的最小整数；R表示实数域。

步骤2步骤1后，系数矩阵H1可以分解H1≈W2H2，其中W2∈Rk1×k2和H1∈Rk2×N

步骤3以此类推，m次分解后，网络邻接矩阵A≈W1W2W3…WmHm，并且W1,W2,…,Wm,Hm非负，

在系数矩阵H上进行m次分解后，矩阵A可以用m+1个因子表示，包括m个基矩阵和一个系数矩阵。每一次添加的基矩阵等价于添加一个额外的抽象层，去自动学习网络层次结构信息，进而更准确、更全面地探索隐特征。深度非负矩阵分解的损失函数可以表示为：

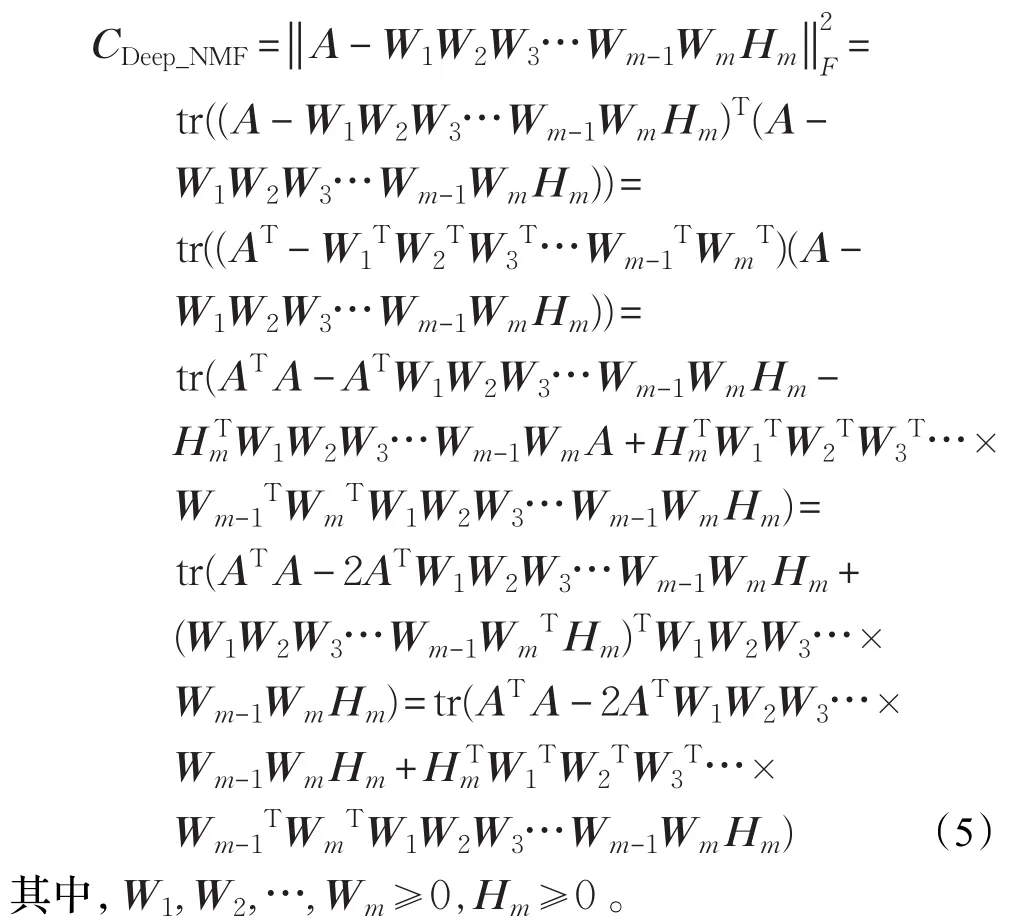
在公式（5）中，让 Λl=[λik]l和 M=[ujk]分别作拉格朗的拉格朗乘数（W≥0，H≥0），其中l=1,2,…,m,λik≥0,ujk≥0 。

拉格朗日函数可以表示为：

基于非负矩阵分解的优化目标函数是一个非凸优化问题，及其预测结果依赖于基矩阵W和系数矩阵H的初始值。传统的非负矩阵分解方法往往随机初始化W和H，但很容易进入局部最优解，这也可能导致欠拟合现象。为了减少链路预测模型的训练时间，提高模型的泛化能力，因此采用了预训练和微调两阶段进行链路预测。

（1）预训练的阶段

步骤1分解网络邻接矩阵A≈W1H1，其中W1∈。

步骤2系数矩阵H1可以分解为H1≈W2H2，其中。

步骤3继续上述步骤，直到所有的层都经过了预训练，网络邻接矩阵A≈W1W2W3…WmHm，其中W1～Wm，H1～Hm是非负的。

（2）微调阶段

对公式（6）的目标函数求Wm和Hm的偏导数，其过程如下：

使用KTT条件0和ujkhjk=0，得到以下方程：

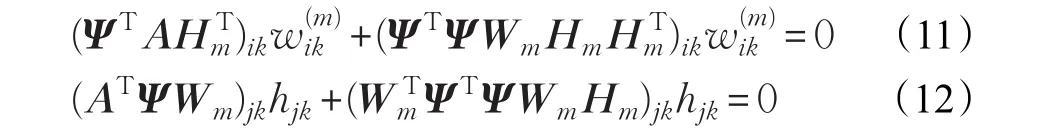
根据文献[14]，可以对Wm和Hm进行以下乘法更新规则：

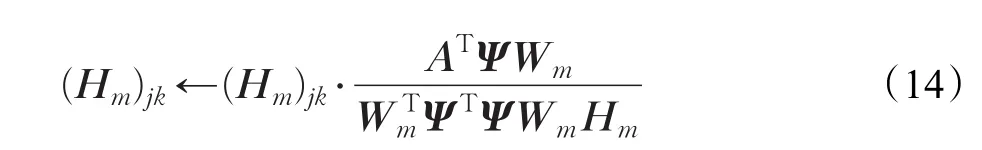
其中，H͂为第m层系数矩阵的重构。

3.3 基于DNMF的链路预测算法

在输入网络数据时，本文提出的链路预测算法有三个步骤。首先通过预训练对系数矩阵多次分解，得到一组基矩阵和一个系数矩阵相乘，进而构建深度非负矩阵分解的目标函数。在分解过程中，确定每层隐特征的数量。然后，通过逐层分解作为预分解结果，再整体微调训练参数，从而实现逐层学习策略。最后，根据微调训练后的基矩阵和系数矩阵重构网络，计算网络相似矩阵，从而构建出基于深度非负矩阵分解的链路预测方法。

算法1基于深度非负矩阵隐特征模型链路预测算法流程：

input：给定网络邻接矩阵A和训练集f的比例，层数m

output：网络的相似矩阵A∗

Procedure计算W,H

根据训练集比例f将A分为Atrain，Atest

forr=1：mdo

获得每层隐特征的数量Kr

until损失函数值小于容差

计算给定网络的相似矩阵A∗

根据A∗=W1W2…WmHm，计算相似度矩阵A*

end procedure

4 仿真实验

4.1 评价指标

为了验证该方法的性能，采用三种评价指标对所提出的方法和基本线方法的性能进行了比较。三个评价指标包括AUC，精度和预测能力（PP），定义如下：

（1）AUC[15]。AUC指标（Area Under the receiver operating characteristic Curve，AUC）是从整体上衡量算法的准确度。AUC可以理解为在测试集中随机选择一条边的存在可能性估计值大于不存在边集随机选择一条边的存在可能性估计值的概率。AUC的具体计算方法如公式所示：

在这里，n表示独立比较的次数，n′表示n′次测试集中随机选择一条边的存在可能性估计值大于不存在边集随机选择一条边的存在可能性估计值，n″表示n″次测试集Etrain中随机选择一条边的存在可能性估计值等于不存在边集E随机选择一条边的存在可能性估计值。

显然，如果所有的存在可能性估计值都是随机产生的，那么AUC≈0.5。所以，AUC>0.5显示了在多大程度上方法比随机选择性能好。

（2）精度[16]。精确度Precision指标定义为算法给出的最有可能存在的前L条预测边中预测正确的比值，其定义如下：

在这里，L是预测可能边的前L条边的数量，一般L取为测试集的边数。Lr是在前L条预测边中预测正确的数量。因此，可以看出精度值Precision越高，其算法的预测准确度越高。

（3）预测能力（PP）[17]。为了刻画预测算法和随机预测之间的差别，文献[17]提出了预测能力评价指标，其也被用于评价链路预测方法的整体预测效果。Prediction-Power指标值越大，说明其预测效果越好。预测能力Prediction−Power（PP）被定义为：

在这里，PrecisionRandom是随机预测的精度值，也就是随机对预测边进行排列，其前L条边预测准确的比例，其平均随机预测的精度值约等于其中N为网络中节点的数量，M为网络中边的数量。

4.2 常用算法的相似性指标

为了验证本文提出的算法的性能，9个典型的相似性指标用于性能比较，包括Katz[18]、ACT[19]、CN[20]、AA[21]、CRA[17，22]、RA[23]、LP[23]、PA[24]和 Jaccard[25]。这些相似性指标的详细描述如表1所示。

4.3 实验数据

为了验证本文提出的方法的性能，考虑以下10个真实世界的网络：爵士音乐家合作网络（Jazz）[26]、网络理论科学家合作网络（NS）[27]、美国政治博客网络（PB）[28]、电力网络（Power）[29]、路由器网络（Router）[30]、论文引用网络（SmaGri）[31]、蛋白质相互作用网络（Yeast）[32]、俱乐部网络（Karate）[33]、高校社交网络（School）[34]。表2提供了以上10个真实网络的拓扑特征。

表2中|V|和|E|分别表示节点总数和边的总数；LD表示边密度，其定义为网络中实际存在的边数与网络中最大可能的边数之比；表示网络节点的平均度（average degree），即所有节点的度的平均值；表示网络的平均最短距离（average shortest distance）；C表示网络的所有节点的接近中心性的平均值；CC表示网络的聚类系数，其等于所有节点簇系数的平均值；r表示网络度-度Pearson相关系数，也称为网络的同配系数；LCP-corr是LCP-correlation的缩写，其表示局部社区范例（Local Community Paradigm，LCP）和CN指标的相关系数[17]；H表示网络的度的异质性[23]。

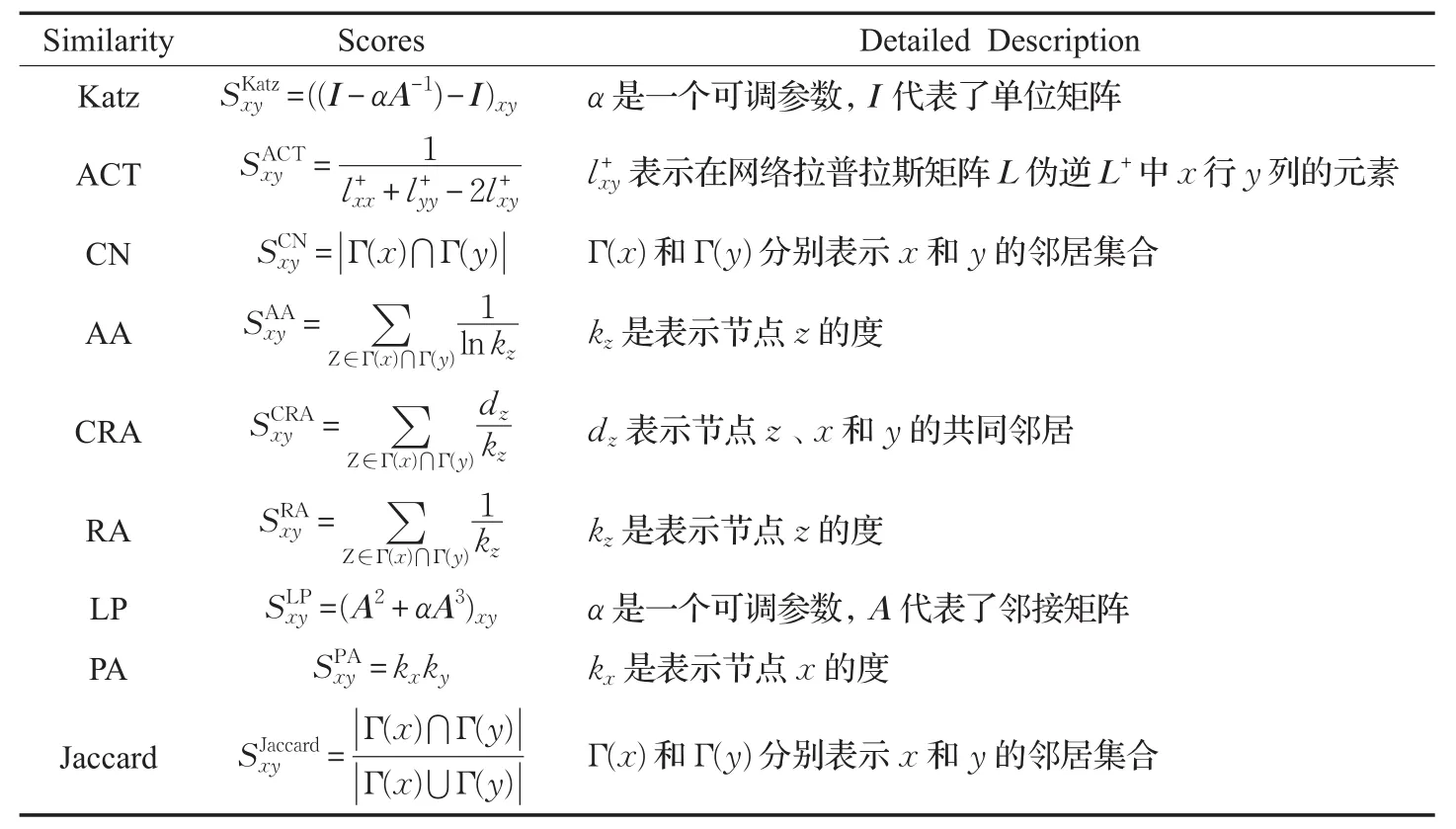
表1 9个典型相似性指标

表2 10个真实网络的拓扑特征

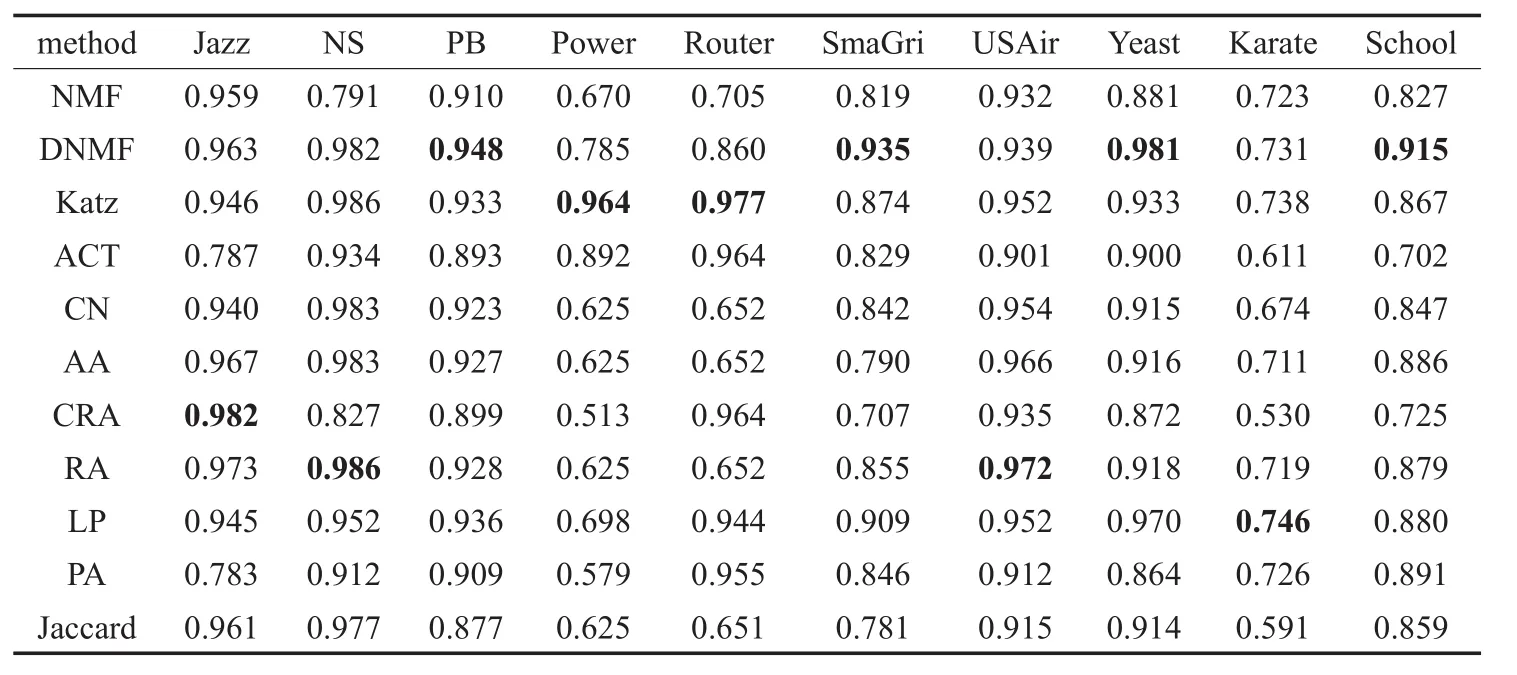
表3 不同方法在10个真实网络上的AUC值

4.4 实验结果

为了测试DNMF方法的性能，将该方法在10个真实网络中与10个经典方法进行了比较。首先，观察到的边被随机分为训练集和测试集。这里，训练集被用于构建预测模型，而测试集仅用于验证在复杂网络链路预测的准确性。

将方法（DNMF）与其他10个网络数据集的方法的AUC、Precision、PP进行了比较，AUC值、Precision值、PP值分别是运行100次的平均值。在实验中，LP方法的参数α为0.000 1，Katz方法的参数α为0.01，DNMF参数m为2。表3、表4、表5中分别给出了不同方法在10个真实网络上的AUC值、Precision值和PP值，每一列的最高值用黑色粗体表示，其训练集比例均为90%。

如表3所示，DNMF优于传统的NMF。此外，DNMF在3个真实的网络中拥有最高的AUC值，包括PB、SmaGri和Yeast。在 Jazz、NS、USAir和Karate这几个网络中，提出的方法DNMF的AUC值也非常接近于最高值。

如表4所示，DNMF比传统的NMF更具有更好的Precision值。DNMF在Jazz、PB、Power、Router、SmaGri、USAir和Yeast这几个网络中拥有最好的Precision值，在Karate和School网络中仅次于CRA方法的精度值。总体来说，它表明，DNMF优于传统的非负矩阵分解和其他经典方法，特别是在稀疏网络上，如Router、PB、Yeast等。

如表5所示，在所有网络中，每个方法的PP的平均值（mean值）在最后一列显示，其也被用于反映方法的整体性能。不同的方法按平均PP值大小倒序排列，由PP的mean值可以看出DNMF的整体性能在11种方法中表现最好。

为了准确测试DNMF方法的性能，分别比较了在6个网络中不同的训练集下的11种方法的AUC值、Precision值、PP值，训练集的比例f从0.3变换到0.9，其结果分别显示在图2、图3和图4中。在图2、图3、图4中这6个网络分别是Yeast、Jazz、PB、SmaGri、USAir和School。

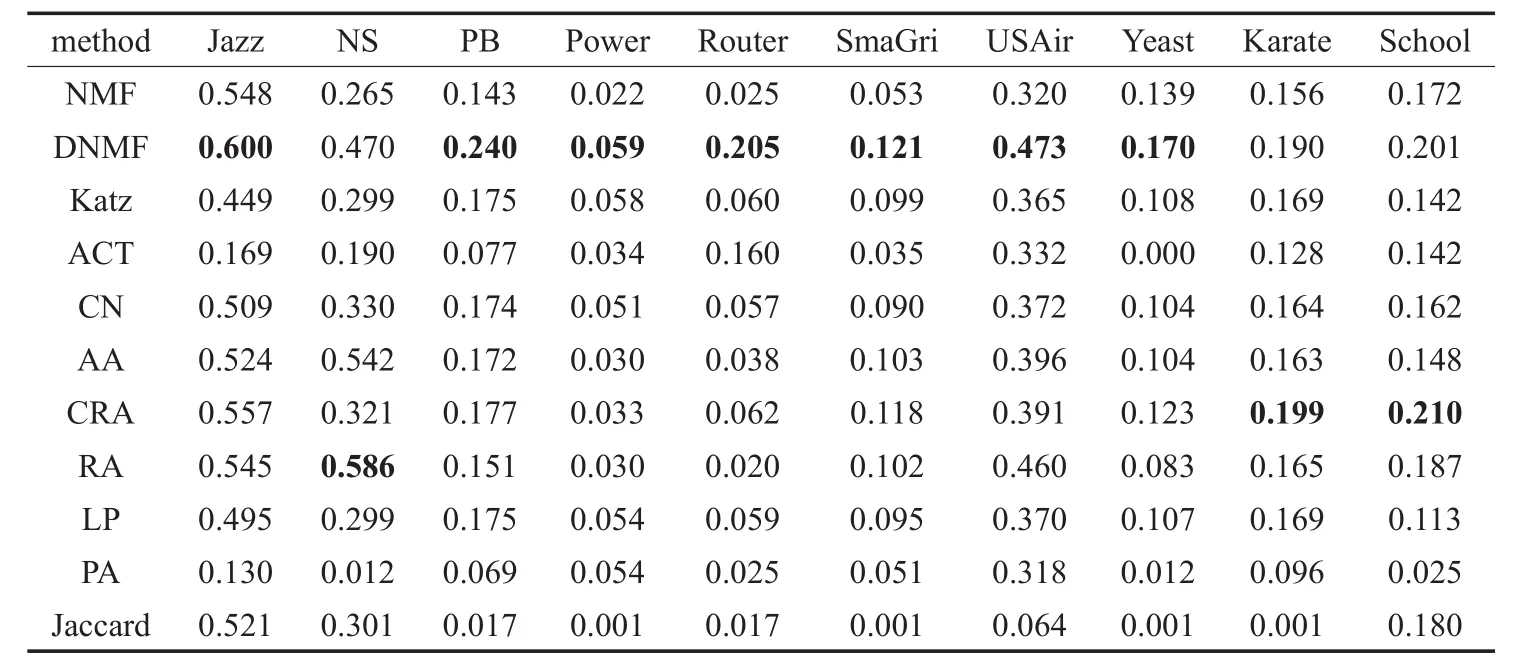
表4 不同方法在10个真实网络上的Precision值

表5 不同方法在10个真实网络上的PP值

从结果可以看出，DNMF方法在大多数网络上比其他方法具有竞争力的性能。综上所述，对于大多数网络来说，所提出的方法DNMF比其他10种典型的预测方法具有更高的预测精度和鲁棒性。

4.5 参数分析

为了分析参数层数m对算法DNMF的影响，选取已被广泛使用的Precision精度作为评价指标，并分别测试了在6个网络中不同训练集比例下m分别取为1、2、3、4时的DNMF的精度，其结果如图5所示。这6个网络分别是Yeast、Jazz、PB、SmaGri、USAir和School。

从图5可以看出，在大多数情况下，当m等于2时，DNMF的精度会比m为1、3、4时的DNMF的精度更高。因此，在通常情况下的实验中设置m=2。

5 结论

真实网络往往是稀疏的，传统的单层非负矩阵分解不能完全描述复杂网络的深层结构，为了解决此问题，本文基于非负矩阵分解和网络的隐特征提出了一个新颖的基于深度非负矩阵分解的链路预测方法。作为非负矩阵分解隐特征模型的扩展，提出的链路预测方法DNMF不仅继承了其优点，也充分利用了多层分解获取网络多组织结构信息。为了验证该方法的性能，本文选取了三个评价指标，分别为AUC、Precision和预测能力（PP）。对10个真实网络的实验结果表明，该模型方法比经典方法具有更高的精度。当然，本文所提出的方法也有一些局限性和改进研究，如何设置参数m在不同网络上进行自适应，以及如何优化算法时间复杂度，将是下一步的工作。

图2 不同训练集下各方法AUC值对比

图3 不同训练集下各方法Precision值对比

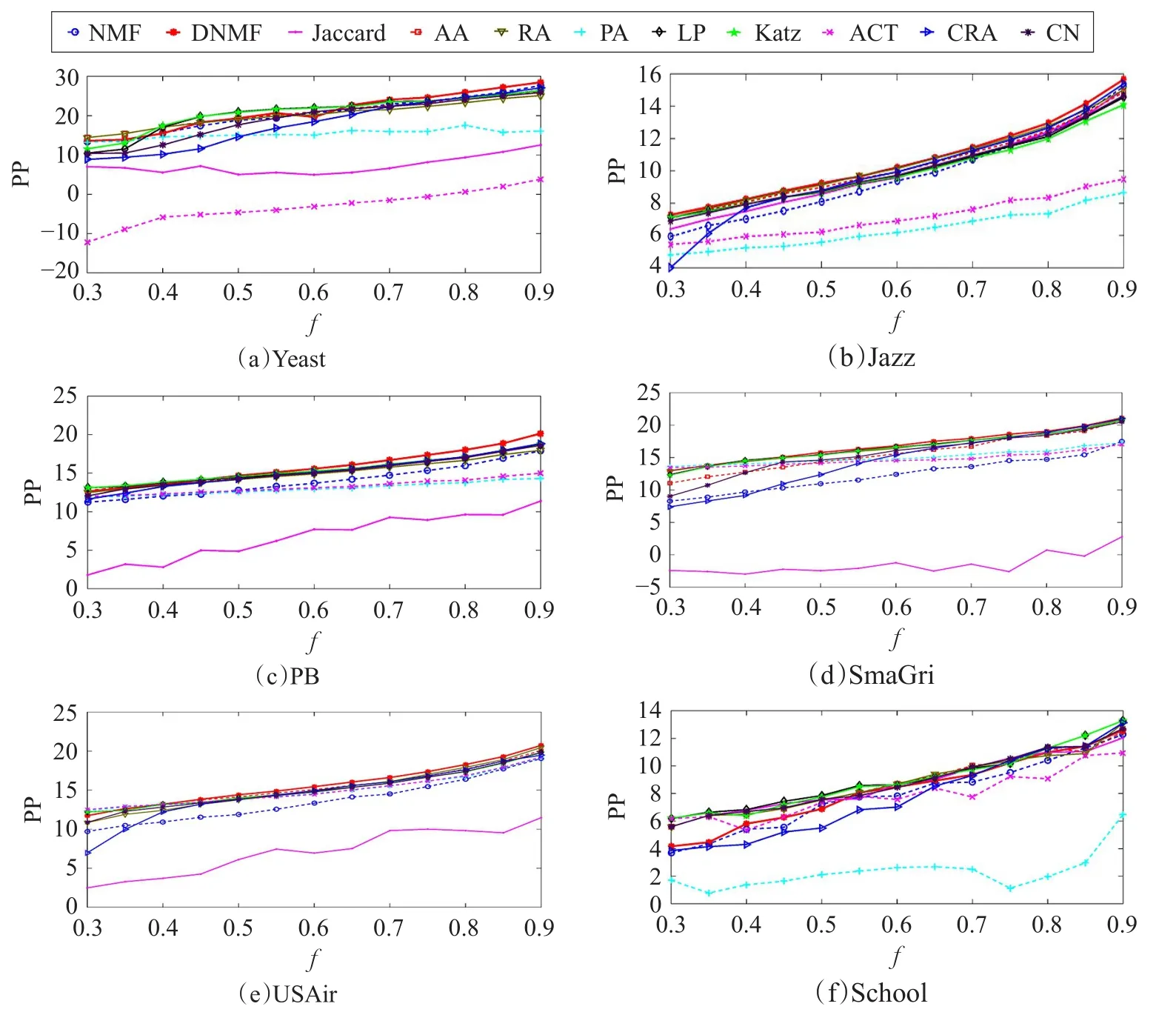
图4 不同训练集比例下各方法PP值对比

图5 DNMF在不同层数参数m下的精度值对比