结合CFDP与时间因子的协同过滤推荐算法

张凯辉，周志平，赵卫东

同济大学 电子信息与工程学院，上海 200093

1 引言

近年来，随着大数据和服务推荐技术的不断发展，针对每位用户的个性化推荐应运而生。因此，在基于大数据时代的背景下，利用收集到的海量用户行为数据，设计出高效的推荐算法，为每位目标用户提供精准高效的个性化服务，便成了要急迫解决的问题[1-2]。

本文研究的协同过滤推荐算法，其原理为：找出数据集中与目标用户兴趣爱好、性格特征或者社会属性相似甚至相同的用户，将这些用户所感兴趣的项目推荐给目标用户。但是，目前传统的协同过滤算法仍然有着许多值得优化的地方。本文重点研究了该算法出现的数据稀疏性问题、冷启动问题和实时性问题。如何更好缓解或解决以上问题，便成了优化协同过滤算法的关键[3]。

本文针对协同过滤算法出现的以上问题，提出了一系列的改进方法：首先采用密度峰值聚类算法（CFDP）对项目进行聚类处理[1]，并用Slope-One算法进行数据填充以解决数据稀疏和冷启动问题；在计算推荐项目评分时引入时间因子来对传统协同过滤算法的评分步骤进行优化，保证了推荐算法的推荐内容具有实时性，可以给予用户更准确的推荐[4]。

2 相关工作

2.1 传统协同过滤推荐算法

算法的基本思想是：根据已有的用户历史行为数据，构造协同过滤矩阵，其中每一行数据代表该用户在所有项目上的评分情况；每一列则代表该项目获取的评分情况。由于算法默认具有相似浏览记录和评分行为的用户，在随后的项目选择和评价上往往也是相似的。传统协同过滤算法的基本运算流程如图1所示[5]。

图1 协同过滤算法流程图

2.2 协同过滤评分矩阵

表1显示了用户-项目协同过滤评分矩阵R，该矩阵为一个m×n阶的评分矩阵，代表共有m位用户n项项目，其中用户对项目的偏好程度用其对项目的评分rij的大小来反映。

表1 用户-项目协同过滤评分矩阵

2.3 用户相似性评价指标

协同过滤评分矩阵中，每一个用户的历史数据都可以提取为一个向量，衡量两名用户的相似性即判断两名用户向量的相似度。一般来说，常用的向量相似度评价指标有：余弦相似性、Pearson相关系数以及修正余弦相似性三种，以下为详细介绍。

（1）余弦相似性

评价用户ui与用户uj的余弦相似度：首先从协同过滤矩阵R中提取用户评价向量vui和vuj，则用户ui与用户uj的余弦相似性为向量vui和vuj的余弦夹角。计算方法如式（1）所示：

其中，ui⋅uj为两个向量的点积，||ui||×||uj||则代表两个向量模的大小乘积。

（2）Pearson相关系数

计算用户ui与用户uj的Pearson相关系数：如式（2）：

其中，Iuiuj代表用户ui与用户uj评论过的项目交集，Ruic代表用户ui对项目c的评分，代表用户ui的平均评分。

（3）修正余弦相似性

由于不同用户打分风格的差异，导致相同喜好用户的评分期望会有很大差异，采用余弦相似度会导致相似度计算结果不准确，修正余弦相似性在计算时不采用评分期望这一变量，很好地规避了该问题，用户ui与用户uj的修正余弦相似性如式（3）：

其中，Iui代表用户ui评价过的项目集合，Iuiuj为用户ui与用户u均评论过的项目交集，为用户u的平均评ji分，Ruic为用户ui对项目c的评分。

一般来说，有两种通用的方法来选取相似用户：阈值法和TOP-N法。其中，阈值法是将计算出的相似性与人为设定的相似度阈值进行比较，若大于则将该用户放入相似用户集合中。TOP-N法则是对所有用户的相似度进行从大到小的排序，选出前N个用户作为相似用户。由于阈值法的阈值不好进行设定，过大或者过小都会影响相似用户选取的质量，所以本文采用TOP-N法来进行筛选。

2.4 项目推荐

从目标用户的相似用户集合U中提取所有目标用户未评价过的项目，并预测这些项目的评分Puij如式（4）：

3 改进协同过滤推荐算法

3.1 传统协同过滤算法推荐算法的不足

（1）数据稀疏问题

一般来说，根据数据集得出的协同过滤评分矩阵稀疏度往往非常高：一般在90%以上。因此，用这样的数据计算出的用户相似度往往是不准确的，由此得到的相似用户也是不准确的，自然也难以得到好的推荐结果[6]。

（2）冷启动问题

由于协同过滤算法是基于历史数据来进行推荐的，对于没有任何历史记录的新用户和新项目，默认与任何用户或项目的相似度都为零，推荐系统也就自然无法将合适的项目推荐给目标用户[7]。

（3）实时性问题

由于用户的喜好或需求是一个不断变化的过程，过去的喜好与当前的喜好可能存在较大差距。因此，将目标用户最近的历史记录与以前的历史记录等价看待显然是不科学的，推荐系统给出的推荐也就难以满足目标用户的当下需求[8]。

3.2 基于密度的聚类算法（CFDP）

根据大量的用户行为数据显示，有着相似兴趣的用户，其兴趣主要集中在有限的几个类型。因此，每位用户的评分一般都集中在一类或几类项目上。因此，本文选择使用Clustering by Fast search and Find of Density Peaks（CFDP）是一种基于密度的聚类算法，将所有项目分成若干个类别。若有新的项目加入，还可以将其聚类到某个大类下面所对应的簇。有效地解决了矩阵稀疏与项目冷启动的问题。

算法的基本思想是：某人聚类中心的密度要高于其周边所有属于该类数据点的密度，且属于该类的数据点对应的聚类中心是距离所有聚类中心中最近的一个。

对于每一个数据点，要计算该点的两个量：局部密度ρi和到具有更高局部密度的点的距离δi。

局部密度计算如下：

其中，dij该数据点与其他数据点间的距离，dc为截断距离，其值一般满足可让点的平均邻居个数约为数据点总数的1%～2%。

距离定义如下：

计算出所有数据点局部密度和距离后，可根据需要的聚类个数选定聚类中心：设定阈值ρmin和δmin，将所有（ρi>ρmin&δi>δmin）的数据点定为聚类中心，一个聚类中心代表一个类别。剩余未被划为聚类中心的点，分别计算出每个点与各个聚类中心的距离，找出距离最近的聚类中心[9]。

3.3 Slope-One算法

Slope-One算法是一种填充矩阵空缺值的算法，其基本思想是：找出矩阵空缺值与已知数值的某种线性关系，利用线性回归的方法计算出空缺值的大小，其具体的计算方法如下[9]。

计算项目i的预测评分P(u)i，首先要计算相关项目j的平均偏差devij，平均偏差devij的计算方法如式（7）所示：

其中，Rij为用户u对项目j的评分，Uij为所有均评价过项目i与项目j的用户集合，Ij为与项目i被同时评价过的项目集合。

项目i的预测评分P(u)i计算方法为：

有一种改进方法是将sum(Uij)作为权值，这样可以保证用户评分次数越多的项目，其预测评分的可信度越高。修正后的预测评分Pw(u)i计算方法分别为：

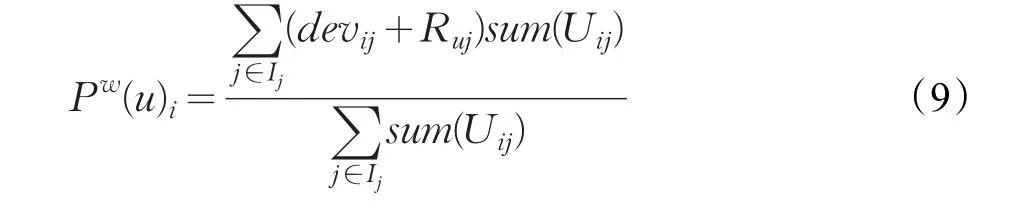
3.4 引入时间因子

目前来说，推荐算法引入的计算因子主要有时间因子、用户关系以及用户信誉度等。在当前各种用户行为数据集中，用户每次行为的时间往往是会被准确记录的；记录用户关系以及用户信誉度的数据集则相对较少，且有可能涉及隐私问题。更为重要的是：推荐算法的目的是为了找出目标用户当前最有可能感兴趣的项目，即目标用户最近的行为数据是最具有价值的数据，引入时间因子可以更好地划分不同数据的价值。因此，本文采用引入时间因子来进行算法优化。

根据上文的分析，时间越近的用户评价越可以反映当前目标用户的兴趣，即用户的兴趣爱好是不固定的，并在某一时间段只会对有限的几个项目感兴趣，并且用户在相隔很短的时间内具有爱好的项目具有更高的相似度。根据以上分析，可以定义用户u对项目i评分的时间权重的计算方法为：

其中，参数α∈(0,1)，通过改变α的值来调整权重大小；Te为用户第一次进行项目评价时对应的时间，Lu表示用户u使用该推荐系统的总时长，Ti表示用户对项目i评分时对应的时间。

但是，根据分析，用户的兴趣变化与时间应该呈现已知非线性的负相关关系。根据研究，用户的兴趣变化与遗忘规律相近，因此本文采用艾宾浩斯遗忘规律作为时间因子的计算方法。则改进的用户u对项目i评分的时间权重计算方法为：

其中，每一个不同时间点的评分项都有一个不同的时间权重，距离当前时间越近的评分时间权重越大[10]。

3.5 改进算法流程

本文提出的改进协同过滤推荐算法，首先采用CFDP算法对项目进行聚类，并用Slope-One算法进行数据填充，有效缓解了传统协同过滤算法的数据稀疏与冷启动问题。在计算预测评分的时候又引入了时间因子，使得对项目的评分更侧重于参考最近的数据。改进算法的具体流程如图2所示[11-12]。

图2 改进协同过滤算法流程图

3.6 改进算法分析

本文针对传统协同过滤推荐算法存在的一系列问题，采用CFDP聚类算法，将相似的项目归为一类，以解决冷启动问题；同时，聚类算法缩减了协同过滤评分矩阵的大小，加快了后面数据填充的效率。针对数据稀疏的问题，本文采用Slope-One算法进行数据填充，填充过后，增加了不同用户之间共同评分过的项目数量，使得在计算用户相似性时有更多的数据可以利用，计算出的结果也就更为可靠。

由于本文提出的算法为推荐算法，需要对目标用户进行实时性推荐。由于用户对项目的兴趣是随着时间而不断变化的，用户很久以前的行为是不具有很大的参考价值的；因此，将某用户的所有行为数据同等对待是不科学的。针对这一问题，本文提出的改进算法引入时间因子，将每个评分项前乘一个时间权重项，从而使计算结果更贴近与最近的用户行为数据，得到更准确的结果[13-14]。

4 实验仿真与结果分析

4.1 实验环境

本实验的开发语言Python3，在Windows10 64位运行。硬件配置：i5-7300HQ，2.50 GHz，内存：16 GB。显卡NvidiaGTX1060（6 GB），硬盘500 GB。

4.2 测试数据集

目前，主流的推荐系统最常用数据集有：MovieLens数据集、Jester数据集和Book-Crossings数据集。Jester数据集为群众对于150个笑话的约600万个评分数据，由于参与评价的笑话数偏少，且没有评分的时间数据，因此该数据集不适合本文的算法仿真；同样，Book-Crossings数据集也没有评分时间，因此也不适合。本实验采用的数据集是MovieLens 1M数据集，收集了共6 000余名的用户对近4 000部电影的100万余条评论，每条评论都有相应的评论时间。评分共有1～5共5个等级，等级越高代表用户对该电影的喜爱程度越高。其中，用户的职业有20余种，电影的种类有18种，数据集的稀疏度为1−1 000 209/（6 040×3 952）=95.81%。

数据集共包含：users.dat、movies.dat和ratings.dat。

用户数据分别有用户ID、性别、年龄段、职业ID和压缩编号5个字段，其中用户ID以及职业ID不需要变，压缩编号本实验并未用到。性别的F和M转换成0和1，年龄转成7个连续的数字0～6，职业转成连续的数字1～20。

评分数据分别有用户ID、电影ID、用户评分和时间戳4个字段。用户、电影ID和用户评分都不需要进行处理，时间戳转化成标准的时间格式。

电源数据则主要有电影ID、电影名称以及电影类型3个字段。电影ID与名称不想要改变，电影类型成连续的数字1～20。

本实验中，本文采用80%的数据作为训练集，20%的数据作为测试集进行试验。

4.3 评估标准

本文采用平均绝对偏差MAE来进行算法评估，指的是所有数据与均值之差的平均值大小，计算方法如下：

其中，pi代表用户u对项目i的预测评分，p′1则代表实际评分。

因此，推荐系统总的MAE为所有用户{u1,u2,…,um}的MAE的平均值[15]，即：

4.4 实验结果分析

本实验对CFDP算法中的超参数dc和时间因子中的超参数α分别取0.2和0.5，且要确定本实验的相似度计算方法、最近邻用户个数K和项目聚类数量N的最优解。

（1）确定相似度计算方法

本文在控制其他变量与流程相同的情况下，采用传统的协同过滤算法，比较各相似性公式下MAE的大小。其中，最近邻用户个数K的取值为10～50，间隔为10，共5个值。实验结果如表2和图3所示。

表2 三种相似性计算方法推荐精度

图3 三种相似性计算方法对比图

从图3可以看出，当采用修正的余弦相似性且最近邻个数K取30的时候，推荐精度最高。因此，本实验采用修正的余弦相似性作为计算用户与项目相似性的指标。

（2）项目聚类数目

CFDP算法通过调整dc来决定聚类种类数目N的大小，使其的取值分别为5、10、15、20、25、30（邻居用户数目K的大小恒为30），实验结果如图4所示。

由图4可知，当聚类数目N取20时，MAE的值最小。因此，将改进协同过滤算法的聚类数目N固定为20。

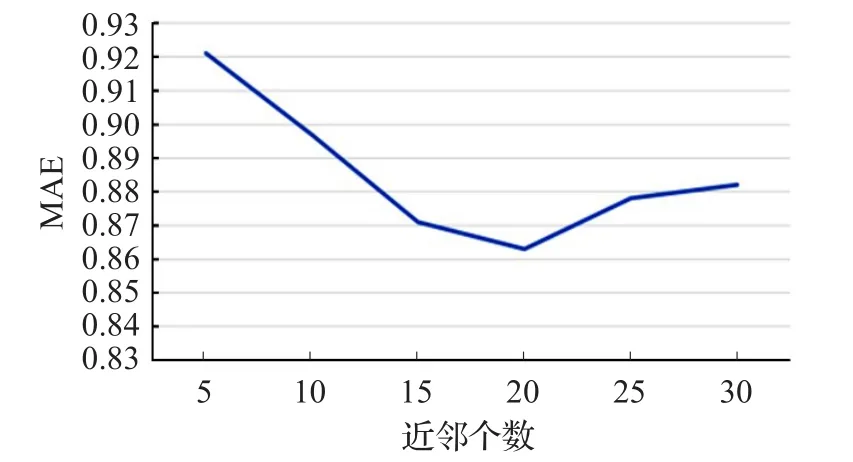
图4 基于项目协同过滤算法聚类个数测试

（3）添加CFDP算法与Slope-One算法

确定最优的聚类数目N后，便要构造新的协同过滤评分矩阵R′，并用Slope-One算法进行数据填充。仿真后的实验结果如表3和图5所示。

表3 两种算法的平均绝对偏差比较表

图5 传统算法与未添加时间因子改进算法实验结果对比图

由图5所示，经过聚类和数据填充后，推荐算法的推荐效果得到了明显的提升。且通过实验发现，由于聚类极大地缩减了协同过滤评分矩阵的大小，推荐算法的推荐速度也得到明显改善。

（4）添加时间因子

时间权重超参数α的确定：

本算法里，本文采用控制超参数α的值来控制时间权重WT(u,i)的大小；且α越小，则距离当前时间较近的用户数据权重比率越大。确定α的仿真实验结果如图6所示。

由图6可知，当α约为0.02时，MAE最小。且由于0.02≪1，说明当前时间较近的数据的确具有更大的参考价值。

比较三种算法的效果，实验结果如表4和图7所示。

图6 α值的影响示意图

表4 两种算法的平均绝对偏差比较

图7 三种算法实验结果对比图

4.5 实验总结

本实验基于MovieLens数据集，首先采用控制变量的方法，找出了超参数邻居个数K与项目聚类数N的最优值。随后，本文对原算法添加CFDP聚类算法和Slope-One算法，并进行了对比实验，证明填充这两种算法的确可以提高协同过滤算法的推荐效果。最后，本文又在改进算法的基础上添加了时间因子。实验结果表明，改进的协同过滤算法的MAE值更低，即推荐效果明显要好于传统的协同过滤算法。

5 结束语

本文针对传统协同过滤算法存在的一系列问题，通过引入其他算法以及改良传统算法的方式，有效缓解了传统算法的存在的一系列问题，得出了更好的实验结果。

不过，协同过滤算法仍然存在很多值得改进的点：（1）单纯地通过矩阵数据的线性关系来填充未知数据的方法是不够严谨的。所以，可以引入其他因子：例如用户的社会属性来进行综合判断。（2）本文提出的改进算法有聚类数目、最近邻个数、推荐结果数目等多个超参数，如何更为准确地得出这些超参数的最优值仍值得研究。（3）随着数据量的增多，推荐系统的速度会越来越慢，如何引入并行计算，提高推荐系统的训练推荐速度也是很值得研究的。