对称α稳态过程驱动的随机微分方程数值分析
胡军浩,高帅斌,刘暐
(1中南民族大学 数学与统计学学院,武汉430074;2 上海师范大学 数学系,上海 200234)
1 相关知识
本文研究了一类对称α稳态过程驱动的随机微分方程的数值解问题,方程形式为:
dx(t)=f(x(t))dt+g(x(t))dB(t)+dL(t),
0≤t≤T,
(1)
初值为x(0)=x0,f:Rn→Rn,g:Rn→Rn×m都是可测函数,L(t)是对称α稳态过程,α∈[1,2).
当方程(1)的系数满足全局Lipschitz条件时,文献[1]讨论了Euler-Maruyama算法. 当α稳态过程L(t)是截断的且漂移项系数Hölder连续时,文献[2]研究了Euler-Maruyama算法. 文献[3]将方程(1)推广至随机泛函方程. 现有文献考虑方程(1)时,漂移项都不是超线性增长的. 但是,随机模型中系数经常会出现超线性,为了填补该空白,本文主要研究这类随机微分方程的数值逼近问题.
文献[4]指出,当随机微分方程系数是超线性时,Euler-Maruyama算法无法收敛. 因此,本文采用半隐式Euler-Maruyama算法. 当L(t)不存在时,方程(1)的半隐式Euler-Maruyama算法已经被广泛研究[5]. 本文的主要不同点和困难是由驱动过程L(t)引起的,它是B(t)的推广,其矩依赖于α. 更准确地说,对于任意的ξ∈[1,α),
(2)
见文献[6]性质1.2.17.

2 基本引理

设(Ω,F,{Ft}t≥0,P)是一个完备的概率空间,其滤波{Ft}t≥0满足通常条件(即它是单调递增和右连续的,并且F0包含所有空集). 设B(t)=(B1(t),…,Bm(t))T是概率空间上的m维Brown运动.
采用如下定义描述α稳态过程[6]. 若随机过程L={L(t)}0≤t≤T满足:
(a)L(0)=0,a. s.;
(b) 对于任何n∈N和0≤t1 (c) 对于任何0≤s 关于方程(1)的系数给出下列假设: (A1) 存在常数K1>0,使得: ∀x∈Rn,q≥2. (3) (A2) 存在常数K2>0和γ>0,使得: |f(x)-f(y)|2≤K2(1+|x|γ+|y|γ)|x-y|2. (4) |g(x)-g(y)|2≤K2|x-y|2,∀x,y∈Rn. (5) (A3) 存在常数K3>0,使得: (x-y)T(f(x)-f(y))≤K3|x-y|2,∀x,y∈Rn. (6) 对于给定的步长Δ∈(0,1)和时间T,定义N=T/Δ. 方程(1)的半隐式Euler-Maruyama算法定义如下: yi+1=yi+f(yi+1)Δ+g(yi)ΔBi+ΔLi, i=0,1,2,…,N, (7) 初值为y(0)=x0,其中ΔBi=B(ti+1)-B(ti),ΔLi=L(ti+1)-L(ti). 由此,yi是x(iΔ)的近似值. 其分段连续数值解为: y(t)=yi,t∈[iΔ,(i+1)Δ),i=0,1,2,…,N. (8) 下面两个引理起着关键的作用. 引理1假设(A1)成立,则对于任意的t∈[0,T],方程(1)的解满足: E|x(t)|q≤C. (9) 证明由It公式和(3)式可知,对于任意的t∈[0,T],有: E|x(t)|q≤ 然后应用Gronwall不等式可得(9)式. 引理2假设(A2)成立,则对于任意的1 (10) 证明对于任意的0≤s 由Hölder不等式,BDG不等式和(2)式可得: (11) 证明由(1)式和(8)式可得: 因此: 在等式两边取平方可得: |x(ti+1)-yi+1|2=A1+A2. 其中: A2=(x(ti+1)-yi+1)T((x(ti)-yi)+ 为了估计A1,把A1拆分成两部分: (x(ti+1)-yi+1)T(f(x(s))-f(yi+1))= (x(ti+1)-yi+1)T(f(x(ti+1))-f(yi+1))+ (x(ti+1)-yi+1)T(f(x(s))-f(x(ti+1)))=:A11+A12. 由(6)式可得: A11≤K3|x(ti+1)-yi+1|2. 由(4)式可得: 因此: |x(s)|γ+|x(ti+1)|γ)|x(s)-x(ti+1)|2]ds. (12) 对于任意的ε>0,有: (1+|x(s)|γ+|x(ti+1)|γ)|x(s)-x(ti+1)|2-α+ε≤ C(1+|x(s)|γ+|x(ti+1)|γ)(|x(s)|2-α+ε+ |x(ti+1)|2-α+ε)≤C(1+|x(s)|2+γ+ |x(ti+1)|2+γ). E((1+|x(s)|γ+|x(ti+1)|γ)|x(s)-x(ti+1)|2)= E[((1+|x(s)|γ+|x(ti+1)|γ)· |x(s)-x(ti+1)|2-α+ε)|x(s)-x(ti+1)|α-ε]≤ CE[(1+|x(s)|2+γ+|x(ti+1)|2+γ)· |x(s)-x(ti+1)|α-ε]≤ 故由(12)式可知: (13) 下面估计A2, 令: 由(5)式可得: |g(x(s))-g(yi)|2≤2|g(x(s))- g(x(ti))|2+2|g(x(ti))-g(yi)|2≤ 2K2(|x(s)-x(ti)|2+|x(ti)-yi|2). E|x(s)-x(ti)|2= E(|x(s)-x(ti)|2-α+ε|x(s)-x(ti)|α-ε)≤ (14) 因此: (15) 由(13)式和(15)式可得: E|x(ti+1)-yi+1|2≤E(A1)+E(A2)≤ 移项可得: E|x(ti+1)-yi+1|2≤ 因此: 利用iΔ=ti≤eCti可得: E|x(ti)-yi|2≤ 根据离散型Gronwall不等式可得: (16) 因此,对于t∈[iΔ,(i+1)Δ),i=0,1,2,…,由(8)式、(14)式和(16)式可得: E|x(t)-y(t)|2≤ 证毕. 考虑下列随机微分方程: dx(t)=(x(t)-x3(t))dt+2x(t)dB(t)+dL(t), (17) 初值为x(0)=x0∈R1. 显然对于任意的q≥2,(A1)成立,即: 另外,由不等式|x|2|y|2≤|x|4+|y|4,∀x,y∈Rn可得: |(x-x3)-(y-y3)|2≤8|x-y|2(1+|x|4+|y|4)和|2x-xy|2≤8|x-y|2, 即(A2)成立. 最后,由(x-y)((x-x3)-(y-y3))≤|x-y|2可知(A3)也成立.




3 主要结论

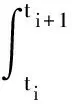
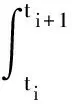
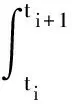




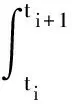


4 实例


