地铁轨道几何不平顺指标预测方法研究

詹璐 刘仍奎 王福田 邱荣华 吕五一

（1.北京交通大学交通运输学院，北京 100044；2.北京交通大学轨道交通控制与安全国家重点实验室，北京 100044；3.北京市交通委员会，北京 100073）

随着地铁运营速度和密度不断提高，在机车车辆动载荷的反复作用下，轨道平顺性状态劣化日益加重。为随时掌握线路动态质量，北京地铁每2月至少进行1次轨检车检测，按照轨距、高低、轨向、水平、三角坑等项目将200 m线路单元区段轨道几何不平顺的动态质量划分为合格、失格2个等级［1］。北京地铁辖内2016年1月至2019年2月的469 000条线路单元区段轨道整体不平顺检测数据中，失格数据为49 399条，占总数据的11%。根据专家经验，这主要是由于北京地铁小半径曲线多，易产生曲线钢轨磨耗，加速轨道平顺性状态劣化，导致轨道几何病害常发。因此，研究轨道几何不平顺指标预测方法，准确预测轨道平顺性状态劣化趋势，对科学编制线路养护维修计划、提高城市轨道交通运营的安全性和舒适性具有重要意义。

国内外学者对轨道几何不平顺指标预测开展了一些研究。Caetano等［2］利用线性回归模型预测了200 m轨道单元区段高低和轨向的不平顺劣化状态和修理周期。Kawaguchi等［3］构建了基于二次指数平滑方法的轨向不平顺状态预测模型，实现了对100 m轨道单元区段轨向标准差的预测。国际铁路联盟利用对数函数拟合了轨道高低不平顺检测值与累计通过总重的关系，预测了轨道高低不平顺的劣化状态［4］。王建西等［5］利用概率分布推移变化矩阵的方法对沪宁线的轨道几何不平顺进行了预测分析。周宇等［6］采用多元回归分析的方法建立了轨道高低不平顺非线性预测模型。

轨道几何不平顺的劣化过程是一个随机过程，相邻2次检测之间的劣化幅度是不确定的（即不确定性）；不同位置的轨道由于受各类因素的影响程度不同，其劣化规律不同（即异质性）［7］。既往研究对轨道平顺状态劣化的不确定性和异质性考虑不足，且研究对象均为干线铁路，不完全适用于地铁轨道几何不平顺指标预测。

本文充分考虑轨道平顺性状态劣化的不确定性和异质性，基于灰色区间预测建模理论进行建模，根据北京地铁轨检车实际检测数据预测轨道几何不平顺指标，并将模型预测值与实际检测值进行对比，以验证模型的有效性。

1 模型构建

1.1 建模思路

将地铁线路以200 m的单元长度划分成若干连续等长的单元区段，针对不同的单元区段建立轨道几何不平顺指标短期预测模型。利用最近一次大修后的历史检测数据，拟合各单元区段轨道几何不平顺指标的变化规律，预测下一次大修前的轨道几何不平顺指标。

本文研究的轨道几何不平顺指标包括轨道质量指数（Track Quality Index，TQI）及轨距、水平、左轨向、右轨向、左高低、右高低、三角坑不平顺等单项轨道整体不平顺（依次表示为TQI1～TQI7）。

以北京地铁的轨检车检测数据为原始数据，基于灰色区间预测建模理论，采用上下限线划分法［8］将原始数据构成上下界序列，构建非等间距GM（1，1）模型，探求轨道几何不平顺指标随时间的变化规律并预测未来的数值。灰色区间预测方法是一种可以很好地应用于复杂因素作用下具有不确定性、异质性等特征的振荡序列的变化规律分析研究的建模方法［9］。利用上下限线划分法建立灰色平面可以避免传统灰平面中主观成分的影响，更真实地反映复杂因素的作用［10］。

1.2 预测模型

构建轨道几何不平顺指标灰色区间预测模型所需的参数及其说明见表1。

表1 预测模型参数及说明

将单元区段i最近一次大修后轨检车检测得到的轨道几何不平顺指标数据序列作为模型输入，利用上下限线划分法确定上、下界序列并分别建立非等间距GM（1，1）模型［11］，得到原始序列的区间预测值和基本预测值。

以上界序列为例，有

1）间 距 序 列 Δt=(Δtu1，Δtu2，···，Δtum)，其 中 ：Δtu1=1；Δtuk=tuk-tu(k-1)，k=2，3，···，m。

3）紧 邻 均 值 序 列Zui={zui(tu1)，zui(tu2)，···，zui(tum)}，其中2，3，···，m。

建立上界序列的非等间距GM（1，1）模型，并利用最小二乘估计法可以得到参数ai，bi的估计值，代入初始条件即可得到时间响应序列

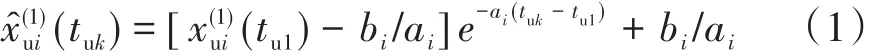
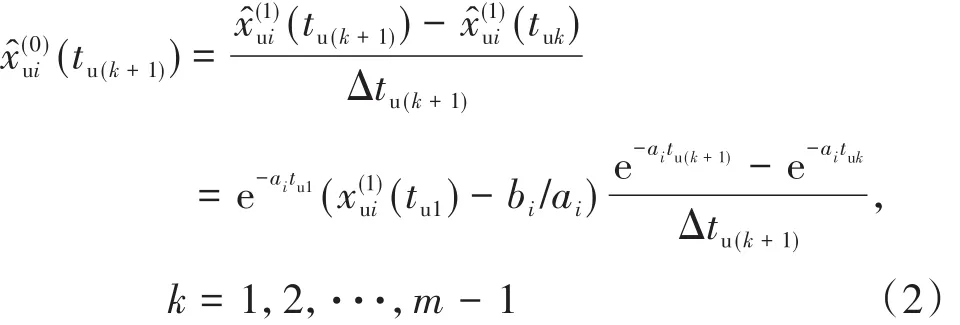
由式（2）可以得到上界序列在tT+k的轨道几何不平顺指标预测值为

同理，构建下界序列的非等间距GM（1，1）模型，得到下界序列在tT+k的轨道几何不平顺指标预测值为

进而得到线路单元区段i的轨道几何不平顺指标在tT+k的区间预测值Si(tT+k)和基本预测值分别为

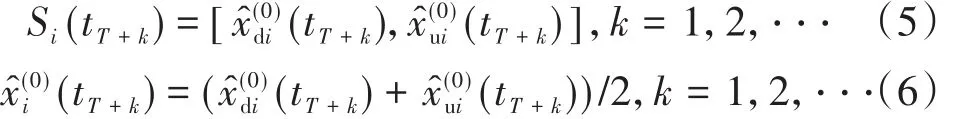
利用上述模型拟合各单元区段的轨道质量指数或单项轨道整体不平顺变化规律，即可得到其区间预测值和基本预测值。

1.3 模型精度检验方法

模型精度可通过计算上下界序列的模拟误差和平均相对误差进行评估［12］。精度检验等级见表2。

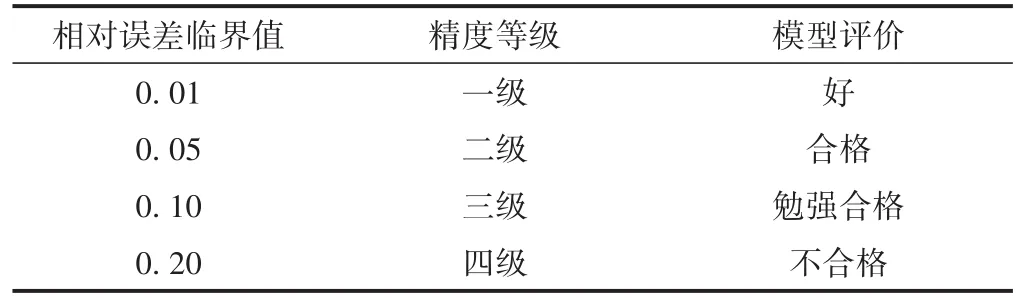
表2 精度检验等级

2 案例分析

2.1 数据准备

收集北京地铁2号线111个线路单元区段2017年2月至2019年2月的12次轨检车检测数据，按文献［1］将各单元区段的各项轨道几何不平顺指标划分为合格、失格2个等级，并统计出各单元区段出现失格的次数（共计1 879次）。本文对出现失格次数最多的10个典型单元区段进行模型验证，其基本情况见表3。以区段1为例，其三角坑不平顺TQI7检测数据见表4。

表3 失格次数较多的典型单元区段基本情况

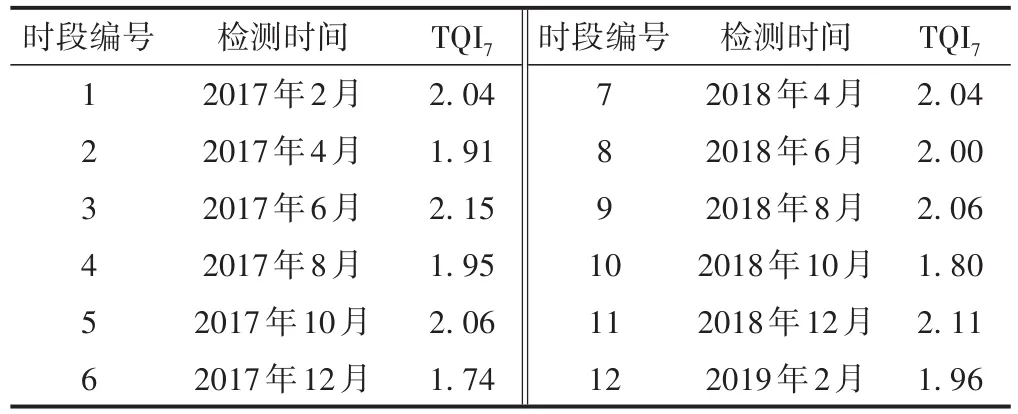
表4 区段1三角坑不平顺检测数据

2.2 模型预测及结果

根据区段1的TQI7数据得出其上、下界序列及上、下界序列的时间响应

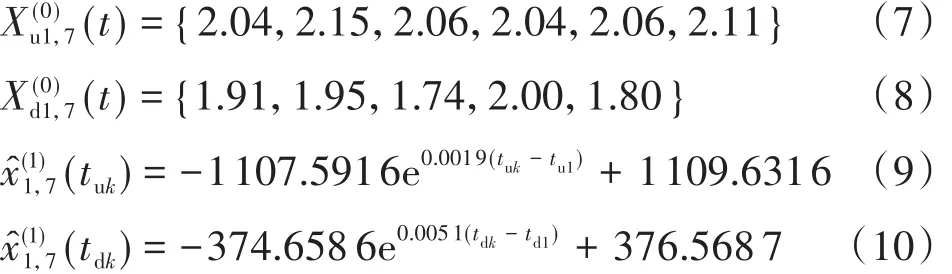
利用式（9）、式（10），得出区段1在2017年2月至2018年12月的TQI7模拟值，并与实际值进行对比，得到上、下界序列的模拟误差，见表5。可知，区段1的三角坑不平顺上、下界序列模拟值的平均相对误差分别为0.017 6和0.050 0。结合表2，模型精度检验等级为合格。

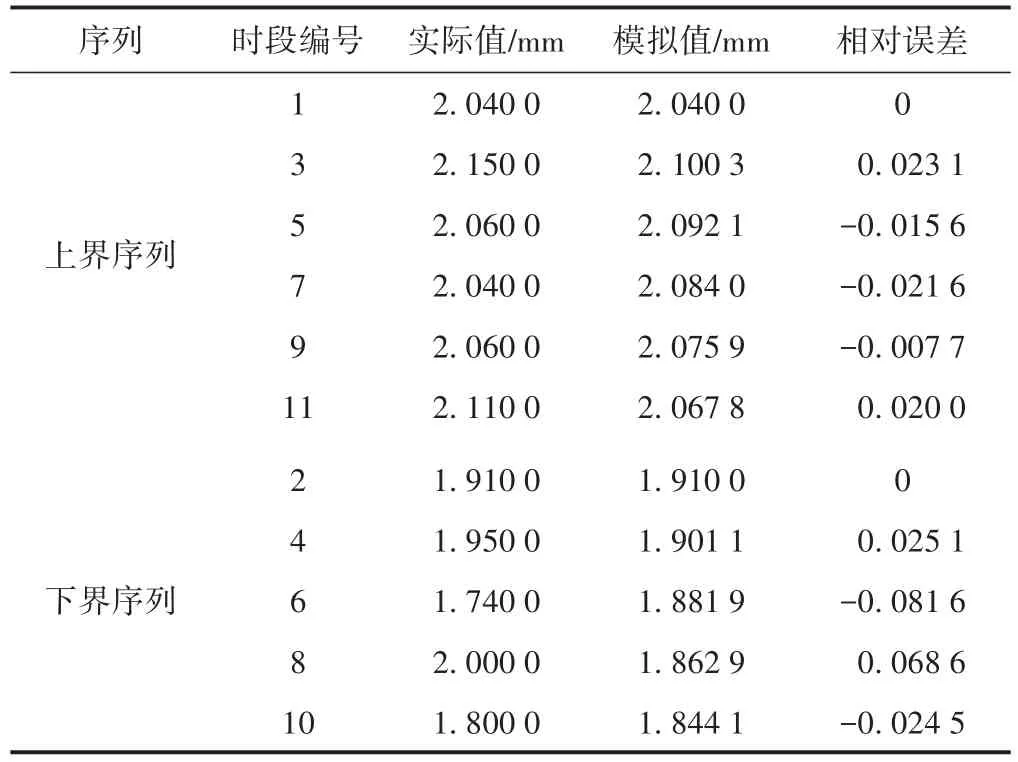
表5 区段1三角坑不平顺模拟结果

利用上述方法拟合区段2—区段10的TQI7变化规律，得出其平均相对误差，并结合表2进行模型精度检验及评价，结果见表6。

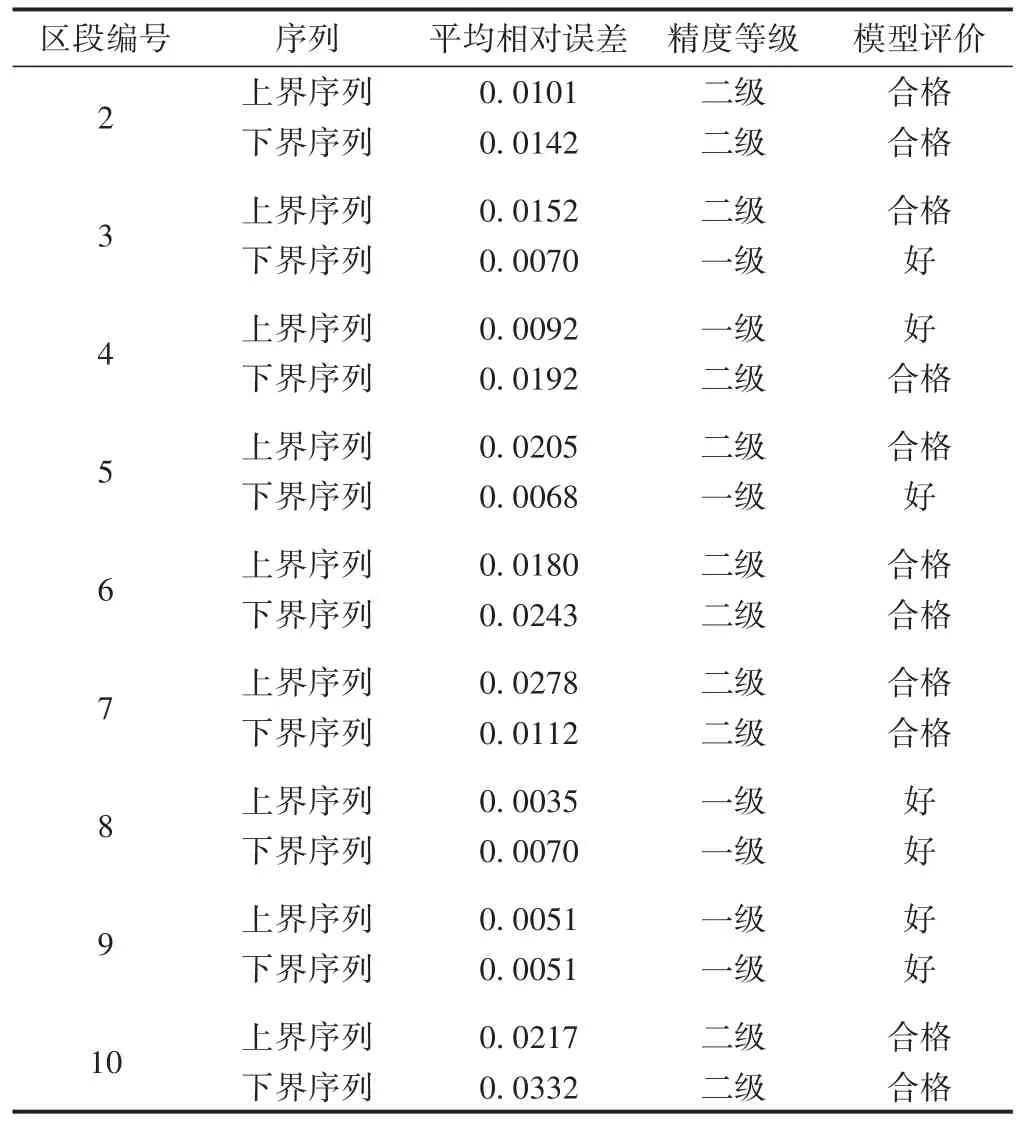
表6 区段2—区段10三角坑不平顺模拟结果

综上，各区段的三角坑不平顺上下界序列模拟的平均相对误差均为合格或好，模型具有较高精度。说明本文构建的轨道几何不平顺指标灰色区间预测模型能够解决轨道几何不平顺状态劣化的不确定性带来的影响，可以用于预测轨道几何不平顺指标。

为进一步验证，对10个典型单元区段在2019年2月的三角坑不平顺指标进行预测，并与实际值进行对比，结果见表7。可知，实际值与预测值的相对误差较小，该预测模型可靠。

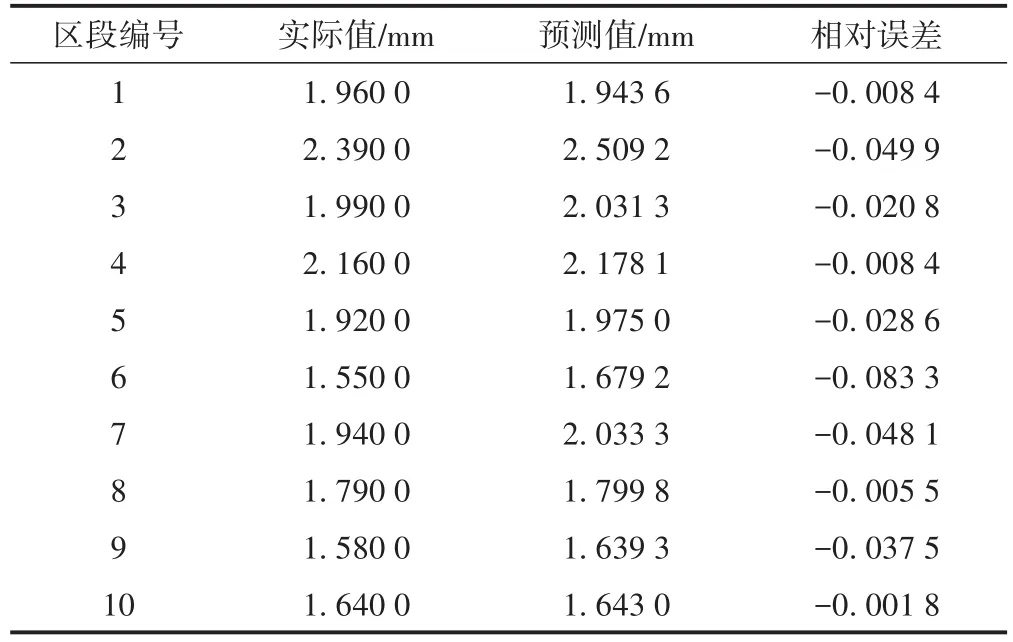
表7 区段1—区段10三角坑不平顺预测结果

3 结语

本文以地铁线路200 m单元区段为分析对象，利用灰色区间预测方法构建了轨道几何不平顺指标预测模型。为了验证模型有效性，利用北京地铁2号线的10个典型单元区段2017年2月至2019年2月的12次轨检车检测数据，对各区段建立相应的灰色区间预测模型。结果表明，所建模型可以较好地用于预测北京地铁轨道几何不平顺指标值，模型预测结果能够满足现场需求。