河南油田注水地层异常压力理论研究

张 悦， 孙冬冬， 王文涛， 狄海公， 张 猛， 陈先超*

(1.成都理工大学能源学院，成都 610059； 2.中国石化河南油田分公司石油工程技术研究院，南阳 473000)

河南油田部分老区块，开发过程中由于注采比长期大于1，使得地层压力逐渐升高，加上储层纵向非均质性强，使得井筒内高压和易漏失层共存，经常在钻进过程中发生溢流、井漏等问题，且溢流发生以后，伴随油气溢出，部分区块气油比较高，容易发生井控失控的风险。因此有必要研究注水井停注泄压的作用及对安全钻井的影响，而泄压半径则是其中的主要内容。

20世纪30年代以来，在钻井中遭遇异常高压并认识到它们是众多钻井事故的主要原因，但当时并未开展压力预测工作[1]；Hottman等等进行了最早的定量压力预测工作[2]；Forster深入了解探讨等效深度法和有效应力法后结合泥页岩的压实作用和地层压力的关系后分析其可行性和存在的问题，奠定了计算地层压力的基础[3]。陈吉永等将d指数法与dc指数法运用到钻井过程中，介绍了实际应用的具体做法[4]。Eberhart-Phillips等建立起地层中声音传播速度与孔隙度、有效应力和泥质含量之间的统计关系[5]。郭齐军等建立了地层压力与声波时差的定量关系，从而通过沉积物中泥岩的声波时差值求取地层压力[6]。张杰等基于油层渗流力学理论建立了更为简单、快捷、准确的调整井压力预测方法，能够满足油田现场实际应用的要求[7]。魏茂安等将支持向量机应用到地层压力的预测之中，取得了很好的预测结果[8]。朱炳兰等为满足调整井钻井需求，借鉴油藏数值模拟理论，利用油田生产的动静态参数分析储层孔隙压力的变化，建立了一套基本可行的调整 井地层压力预测理论、方法和计算模型[9]。胜亚楠等结合测井资料、地层层序学、概率统计等相关理论和方法，建立含可信度的地层压力的求取方法，使得地层压力的解释结果不在是一个单值，而是一个概率区间[10]。李彦婧等以单井测井资料为基础，用实测数据作为约束，对比Eaton法和改进的Fillippone法压力预测结果，选择改进的Fillippone法为工区的压力预测模型并确定公式经验值[11]。这些年来，中外许多专家学者对调整井地层压力的计算方法进行了研究，提出了大量的计算公式，随着技术发展，新的钻井、录井、测井和地震方法层出不穷，大大提高了地层压力预测的准确度[12]。但是，针对具有指导意义的理论图版到现在还没有系统的研究。

通过对井网条件下的钻关水井波及范围、降压规律进行深入的分析，根据渗流力学理论，建立注采单井组停注泄压理论解析数学模型，提出泄压半径的概念，并根据无因次变换绘制泄压半径理论图版。同时利用数值模拟建立理论模型，分析注水开发下影响压力变化的主要因素，最后利用数值模拟数据也建立泄压半径理论图版，二者相互验证，对复杂油气藏开发中后期安全、高效地钻井具有重要指导意义。

1 解析模型

1.1 注水井泄压半径理论模型

考虑一注一采情况，正常的注采关系下注水井与采油井之间存在一个地层压力分布曲线的拐点(一般该点压力为原始地层压力Pi)，该拐点与注水井之间的距离即为注水井泄压半径。利用压力叠加原理，经过注水时间t后距离注水井r处地层压力P(r,t)为

(1)

式(1)中：Q1为注入量，m3；Q2为产液量，m3；Bw为水体积系数；Bo为油体积系数；L为注采井距，m；t为注水时间，s；μ为流体黏度，mPa·s；K为储层渗透率，μm2；h为储层厚度，m；η为导压系数，cm2/s。

利用式(1)可以分别求出注水井注入压力Pwf1和生产井井底压力Pwf2：

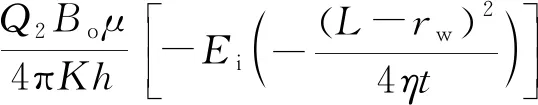
(2)

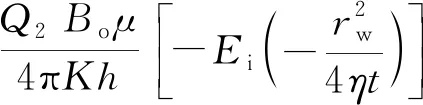
(3)

假设泄压半径为re，那么泄压半径处地层压力等于初始地层压力，则：

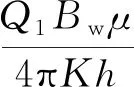
(4)

(5)

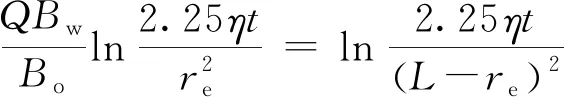
(6)

1.2 注水井泄压半径理论图版

为了使制作注水井泄压半径理论图版有更广的应用范围，定义以下无因次变量来制作对应图版：

泄压半径求解公式可以写为

(7)

利用式(7)制作一注一采注水井无因次泄压半径理论图版如图1所示。

图1 解释模型注水井泄压半径理论图版Fig.1 Theoretical chart of relief radius of injection well of analytical model

从图1可以看出，当地下注采比大于1时，无因次泄压半径均大于0.5，而且随着无因次波及面积的增大，无因次泄压半径逐渐增大。本图版可以根据计算出的无因次传播面积查阅不同注采比下的无因次泄压半径，从而指导加密井的部署以及开关泄压井的位置。

2 数值模拟

2.1 基础模型介绍

模型采用单层平面均质模型(图2)，采用规则五点法井网，一注四采，井距为200 m；其他如高压物性、相渗曲线、岩石及流体性质等数据均借用河南油田某区块的数值，如表1所示。网格划分30×30×6，平面步长10 m×10 m，纵向上根据实际单层厚度设置。

图2 理论模型形状Fig.2 The shape of theoretical model

表1 模型基本参数

2.2 注水压力影响因素分析

模型建立之后设置各种参数变量，依次考虑注水情况下的油水黏度比、开发年限、注采井距、平面非均质性、纵向非均质性对压力的影响。

2.2.1 油水黏度比

由于地下水体的黏度基本不改变,因此设置不同黏度比是通过改变油相黏度实现。模拟预测10年后各情况下的压力情况如图3所示。

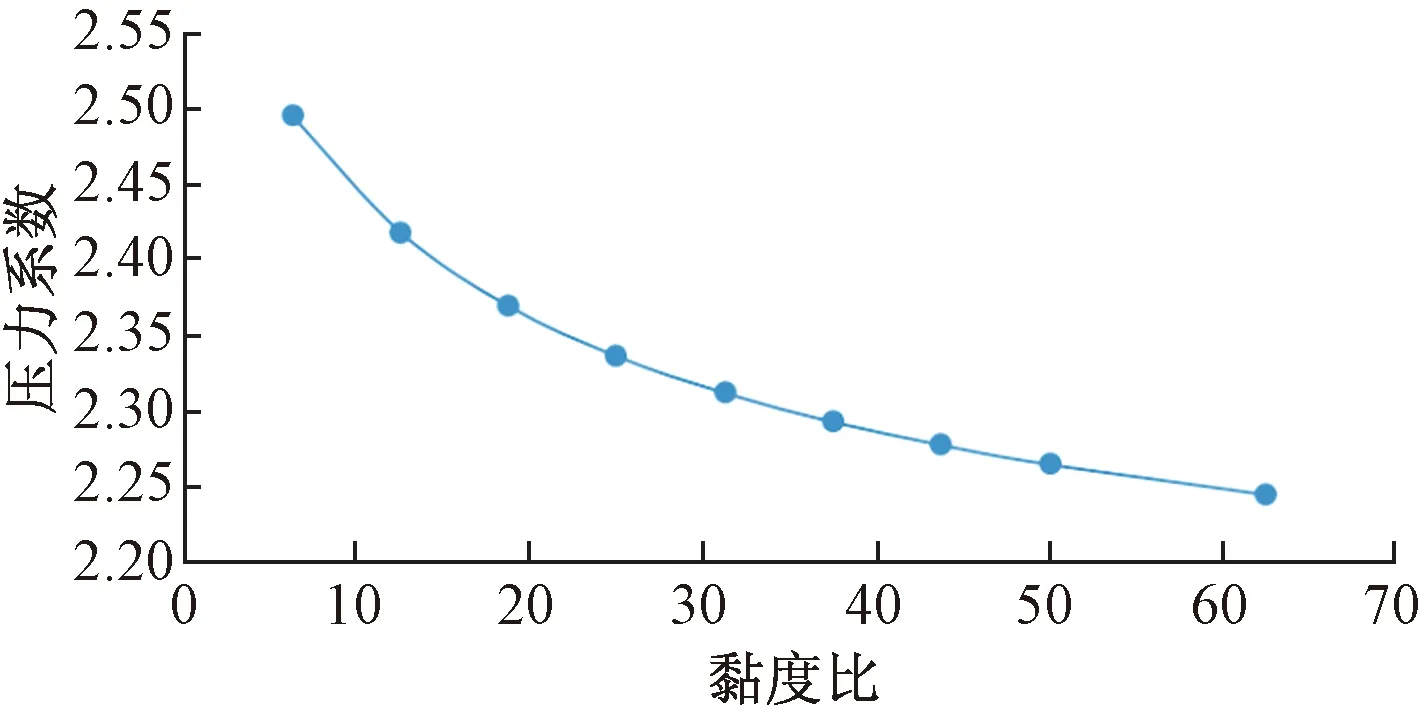
图3 不同黏度比下压力系数变化图Fig.3 Diagram of pressure coefficients with different viscosity ratios

图3显示，随黏度比增加，注水地层压力系数会逐渐减小，且逐渐平稳。原因在于油相黏度越小，与水相黏度越接近，流度比越接近于1，波及体积越大，驱替效率越高，剩余油越少。水相体积系数为1.02，因此在地下留下的水体越多，压力相对则越大。

2.2.2 开发年限与注采井距

开发年限与注采井距分析过程与油水黏度比类似，如图4所示，做简要分析。

图4 不同开发年限、注采井距下压力系数变化Fig.4 Change of pressure coefficients with different viscosity ratios and different producer-injector spacing

图4(a)显示，随着注水时间的增加，压力系数逐渐增大，原因很显然，因为注采比为1.1，随着时间推移，地下水体逐渐累积，压力自然不断增加。从图4(b)上看出，随着注采井距的增加，压力系数不断降低且趋于稳定。分析原因是在增加井距的同时布井方式仍是一注四采，面积增大后储量增加，驱替距离增加，重点是压力展布面积增大，即注水体积增加后平均下来的压力值相对更小，所以压力增加程度随着井距增加而减小。

2.2.3 平面非均质性

平面非均质的种类有很多，主要是储层渗透率差异，此处模拟了几种典型情况，包括断层控制、高渗条带、井网不完善以及采液量差异如图5所示。

就断层控制而言，在一个三角区域有断层控制后，容易形成一个相对封闭的空间[图5(a)]，流体很难直接流通，波及系数会降低，若此处生产井不断生产，地层体积亏空等不到弥补，那该处就会形成异常低压。

如果在地层中存在高渗条带，且在生产势流通道上，流体自然会优先选择高渗通道，但高渗通道两端生产井采液速度有限，高渗通道内会聚集流体，达到一定界限后才会逐渐向低渗区域波及。因此，在高渗区域容易形成高压，低渗区域易形成低压[如图5(b)]。

除了储层因素，在生产控制上也会有一些造成地层高压、低压的因素。最主要的是注采比问题。正常情况下，如果生产过程中注采比长期大于1，那长时间后地层自然会形成异常高压。除此外，若井网控制不完善，在不完善区域容易堆积液体形成高压区域[图5(c)]；在采液量差异方面，若各方向渗流能力一样，那采液速度大的区域易形成低压，采液速度小的区域易形成高压[图5(d)]。

2.2.4 纵向非均质性

河南油田某实际储层分为22个含油单层，根据临层相似性分为6层，理论模型也分为6层，厚度与实际一致，根据实际情况设置渗透率，如表2所示。预测结果显示，压力系数与渗透率呈正相关，因为注入流体优先进入高渗层，单层渗透率越小，流体渗流越加困难，波及系数越低，压力波及越慢，压力系数越小。

2.3 注水井泄压半径理论图版

在前面解析模型中已经定义了几个无因次变量，并且利用泄压半径求解公式做出了理论图版，而在此处，结合数值模拟中的具体数据，利用无因次泄压半径RD和无因次传播面积AD计算公式算出横坐标和纵坐标的值，画出不同注采比下的变化曲线如图6所示。

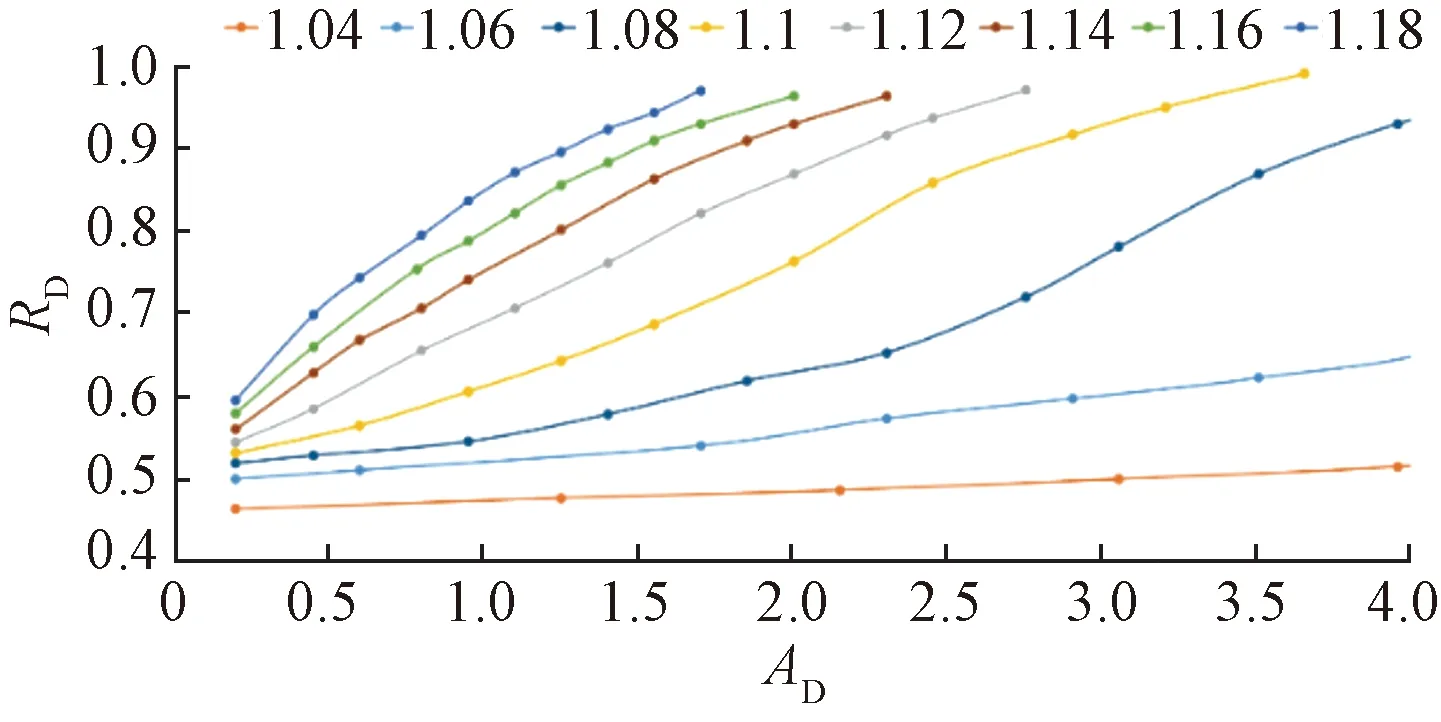
图6 数值模拟注水井泄压半径理论图版Fig.6 Theoretical chart of relief radius of injection well of numerical simulation

对比解析模型和数值模拟得出的泄压半径理论图版可发现，解析模型属于纯理论，因此图版中曲线平滑度及趋势变化很一致，而数值模拟得出的图版显示，各曲线变化趋势大体一致，但增长幅度有一定区别。解析曲线中无因次半径增长缓慢，在无因次传播面积1～4的变化范围中，无因次半径变化范围仅为0.5～0.65；而数值模拟图版中，随着注采比增加，水驱前缘传播速度加快，因此无因次半径在短时间内就接近1。分析原因为理论模型中更偏重于单相流动，而数值模拟则是完全模拟实际生产的两相流动，在流体黏度、体积系数方面有很大差别，两相条件下，流体地下体积会相对更大，从而导致压力系数增加速度加快。两幅图版虽有一定差异，但是相互验证后无太大差距且结论一致，均对油田加密井部署及压力预测后的泄压范围控制具有指导作用。

3 结论

(1)建立了一注一采注水井供液半径数学模型，绘制了不同注采比下的无因次传播面积与无因次泄压半径关系的理论图版。

(2)利用数值模拟建立理论模型，结合现场实际数据分析了注水地层影响地层压力的因素，同时也建立了不同注采比下的无因次传播面积与无因次泄压半径关系的理论图版。

(3)两幅图版相互验证，虽有些许差异但趋势和结论一致。结果显示：当地下注采比大于1时，无因次泄压半径均大于0.5，且无因次泄压半径随无因次波及面积的增大而增大。本图版可以根据计算出的无因次传播面积查阅不同注采比下的无因次泄压半径，从而指导加密井的部署以及开关泄压井的位置。