利用水准数据的天津市地面沉降时空特征分析

常 明，尹海权，苏广利，田 晓，徐玉健

(中国地震局第一监测中心，天津 300180)

地面沉降是区域性地面高程降低的环境地质灾害，具有沉降速度相对较慢、难以察觉、持续时间长、影响面积广、防治难度大、几乎不可恢复等特点。地面沉降会导致楼房墙壁开裂、地基下沉、铁路路基下沉的问题，给人们的生产、生活造成巨大损失[1-3]。针对地面沉降的监测和分析已经越来越引起人们的重视。

造成地面沉降的因素分为自然因素和人为因素。其中，自然因素主要包括地壳运动、地震、地质灾害等，具有地质构造发生变化使得地面出现相应的形变特征[4-7]。人为因素则分为外部因素和内部因素。其中，内部因素主要包括地下水、石油、天然气及矿物质等地层物质的长期超量开采；外部因素则主要是大规模的施工建设导致的地面高程变化。目前我国遭受地面沉降灾害的城市超过50个，地下水的过量开采是导致我国城市地面沉降的主要原因[8-13]。

国内许多学者借助多种观测手段对地面沉降情况进行观测，并借助趋势面分析等算法模型对地面沉降情况进行了分析处理。文献[14]利用InSAR手段对北京地面沉降的时空分布特征进行了分析。文献[15]利用GPS对天津市沉降情况进行处理并与水准观测结果进行比对，证明了GPS在平原区域对沉降情况进行监测的可行性。文献[16]利用目标层次分析法构建了沧州地区地面沉降风险评估指标体系，并对指标体系进行定性分析，借助GIS将沧州分成了高中低3级地面沉降危险区。文献[17]以温黄平原为例，借助多种模型算法对离散沉降观测数据进行拟合，构建地面沉降量与时间序列的关系，为地面沉降预测模型选择和沉降监测防控提供了依据。文献[18]综合考虑建筑物荷载对地面沉降的影响，对Kriging差值方法进行改进，准确反映了沉降形变量大小和趋势。文献[19]在趋势面拟合的基础上添加时间序列，构建三维动态趋势面模型，获得了良好的时空插值结果，并使用GPS沉降监测网数据对地面沉降情况进行了分析。

虽然目前有多种观测手段用于地面沉降监测，但水准观测是最准确、最能直观反映地面高程变化的观测手段之一。通过测量地面水准点的高程变化，可以反映地面的沉降变化。自1923年天津市经历了地面沉降的萌芽期、沉降中心的形成、地面沉降快速扩展几大阶段，直至20世纪70年代才开始针对地面沉降进行研究、治理。目前天津市已经成为我国北方地区地面沉降最严重的城市之一，持续的地面沉降导致经济的发展受到损失、人们的生活受到威胁[20-22]。本文采用2005—2012年、2016—2017年水准观测数据，利用扩展卡尔曼滤波模型对观测数据进行滤波，求解沉降量、沉降速率及沉降加速率，构建多项式加权内插模型，对天津市地面沉降的时空特征进行分析。

1 水准监测情况概述

天津市地处华北平原东北部，渤海西岸，除蓟县外均为低山丘陵。为了避免降水等其他自然因素造成地下水位变化从而导致地面沉降的情况，天津市的地面沉降动态监测一、二等水准测量工作都会选择在每年8—10月进行，其中一等水准路线长度约1300 km。考虑地形的影响，一等水准点的布设主要集中在东丽、大港、塘沽等除蓟县以外区域。具体分布如图1所示。

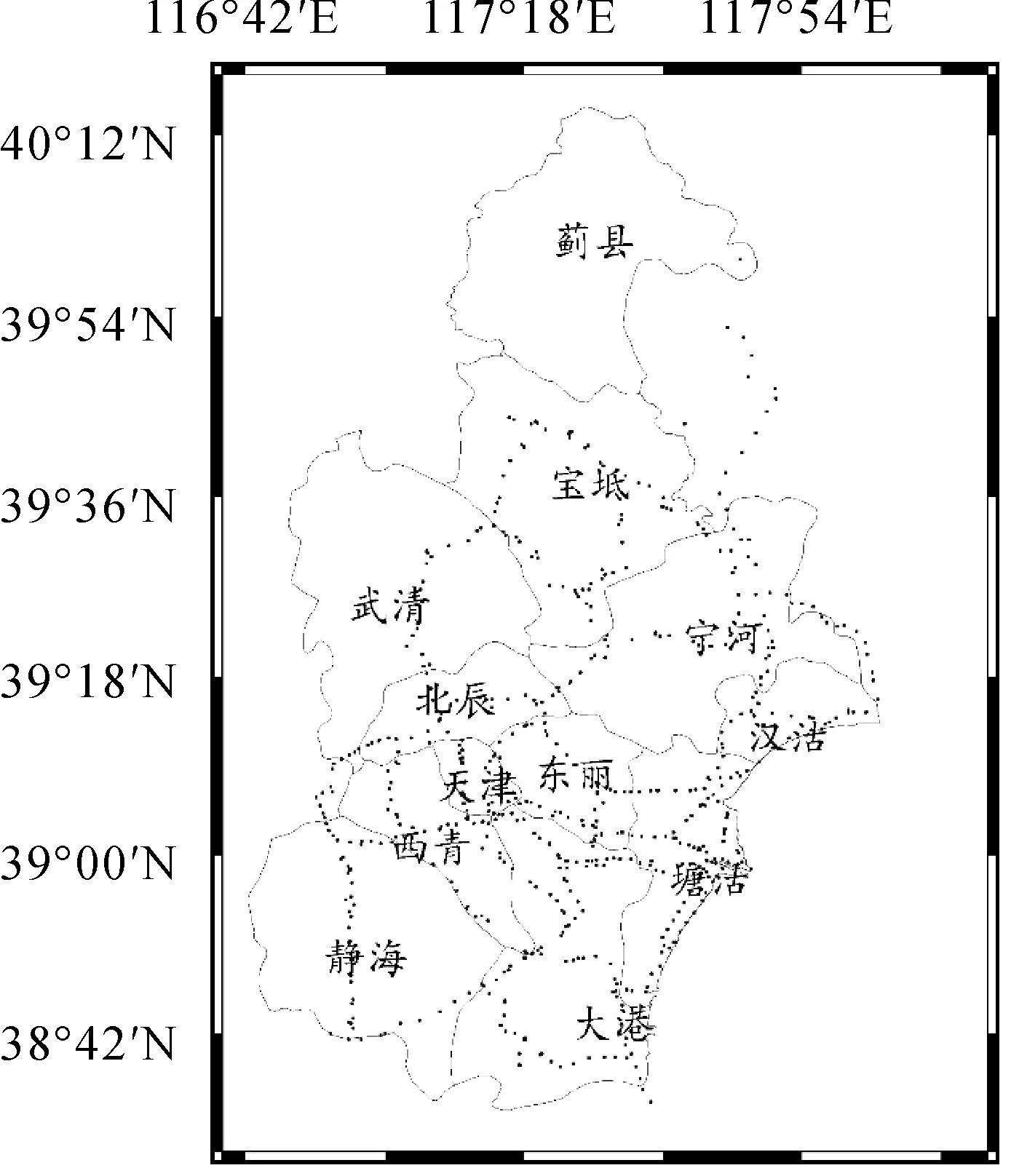
图1 天津市水准点分布情况

随着城市的快速发展，碍于施工影响，部分水准点遭到破坏，需要重新埋设。为了保证数据的连续性，本文选择收集水准观测成果中未被破坏的水准点进行地面沉降分析。

2 卡尔曼滤波模型

地面沉降过程可以看作是一个动态系统，因此水准数据是动态测量平差的过程。选择一个合适的动态数学模型对其进行数据处理能够更加准确地获取地面的沉降信息。水准测量的观测方程模型为

L=BX+Δ

(1)

式中，L为观测值；B为已知系数矩阵；Δ为观测误差向量，即观测噪声向量。因此求矩阵X的过程即为测量平差。在测量平差中，含有误差的观测值求解参数的最佳估值方法分为两种：最小二乘平差法和滤波。由于滤波考虑了参数的随机性质，因此当已知参数的先验特性时，所得到的估值比经典最小二乘的方法具有更高的精度。地面沉降可以理解为处于运动中的地面控制点与时间t的函数。为了能够更好地对天津市沉降信息进行描述，本文以沉降量、沉降速率、沉降加速率作为状态向量，构建状态方程式如下

Xk+1=Φk+1,kXk+Γk+1ωk

(2)

式中，Xk为k时刻的状态向量；Xk+1为k+1时刻的状态向量；ωk为随机干扰；Φk+1,k为状态转换参数,则

(3)

式中，h为某一水准点位的高程；v为沉降速率；a为沉降加速率。

Φk+1,k为状态转移矩阵

(4)

卡尔曼滤波的观测方程式可表述为

Lk+1=Bk+1Xk+1+Δk+1

(5)

式中，Lk+1为k+1时刻的观测值；Bk+1为k+1时刻的已知系数矩阵；Δk+1为k+1时刻的观测误差。

随机模型为

(6)

在水准观测测量中，假设某一个控制点i在t时刻的沉降信息为ξi(t),其沉降瞬时速率为λi(t)，将地面沉降的瞬时加速率Ωi(t)，则

(7)

(8)

针对一个控制点的状态向量的描述可认为是沉降信息、瞬时速率及瞬时加速率的函数，记为

f(ξi(t),λi(t),Ωi(t))

(9)

令i点的状态向量为Xi(t)，所有水准的状态向量记为X(t)，则天津市的沉降水准观测网的状态模型可以表述为

(10)

水准测量中，以观测点的高程和沉降速率为状态向量，则状态方程和观测方程为

(11)

hi(k+1)=Bk+1Xk+1+Δi(k+1)

(12)

通过以上两个方程可实现对天津市水准数据的滤波，得到水准观测点的沉降量、沉降速率、沉降加速率。

3 地面沉降空间分布

水准观测获取固定点相对高程的变化，为了更加直观地表现沉降的空间分布特征，本文针对求解的参数对沉降信息进行内插。常见的内插数据模型有很多种，主要包括反距离加权插值、线性内插等函数模型。

3.1 反距离加权插值

反距离加权插值是对于当前插值点i，选择一定大小l的窗口。对窗口内的观测点集Pn的沉降量按照距离倒数k次方的方法进行加权计算，k值可以根据实际大小进行选择。具体公式为

(13)

式中，hi为内插点沉降量；hj为点集Pn中第j个点的沉降量；dij为观测点与目标点之间的距离；σ为平滑因子，一般取为0.002；k为权的方次，一般可取为1。

3.2 线性内插

线性内插是假设试验区域内的沉降量为线性变化，内插点i的取值认为是关于经度、纬度的函数，公式为

hi=a0+a1Bi+a2Li

(14)

式中，Bi、Li为内插点的经纬度。

3.3 多项式加权内插

地面沉降并不完全呈线性变化，且内插点沉降量的大小并不仅仅受距离的影响。距离、沉降速率、沉降加速率都是影响内插点沉降的因素。因此本文针对目标内插点i，选择一定大小的窗口，并提取窗口内观测点滤波后的状态向量，构建多项式加权内插模型，对目标点的沉降量进行求解，公式如下

(15)

式中，hi为目标内插点i的沉降量；hj为窗口内点集Pn中观测点j的沉降量；δij为观测点j的权重；θij为由距离解算的权重；Δvj为观测点j的沉降速率；Δaj为观测点j的沉降加速率；dij为观测点与目标点之间的距离；σ为平滑因子；k1、k2、k3分别为距离、沉降速率、沉降加速率的方次。

通过窗口的不断移动，由以上公式实现对试验区域内每个点的沉降量进行求解。

3.4 精度评定

本文利用观测数据中80%作为试验数据进行内插，利用20%作为验证数据进行精度评定。通过比较验证数据与内插数据的偏移量的绝对值，验证多项式加权内插的准确性。统计结果见表1。

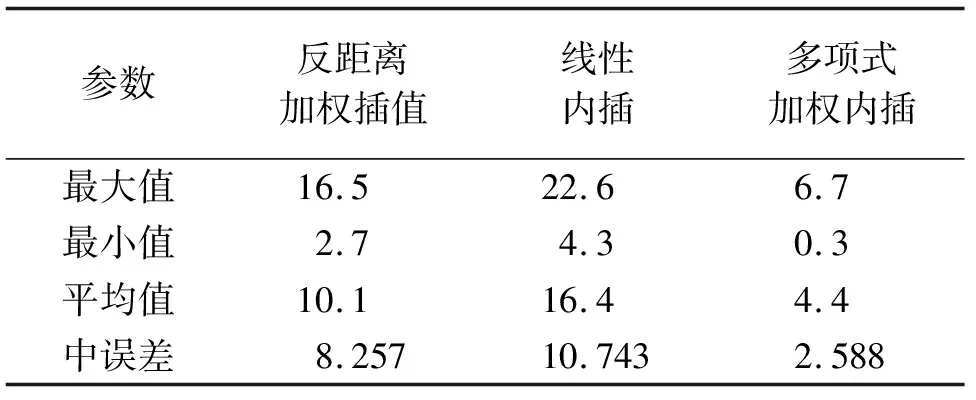
表1 试验数据内插结果统计 mm

通过试验数据的比较分析，多项式加权内插相比于其他方法具有更高的精度。

4 试验分析

对天津市水准观测数据进行滤波，并利用本文提出的内插方式进行处理分析发现，2005—2017年天津市整体区域累计形变量分布情况如图2所示，最大形变量为1 143.5 mm；累计平均形变量为394.477 5 mm。以北辰区西部、汉沽区南部、静海中部、东丽南部、大港中部、西青南部为中心，呈现漏斗式区域下沉结果，其中以北辰区地面沉降情况最为严重。

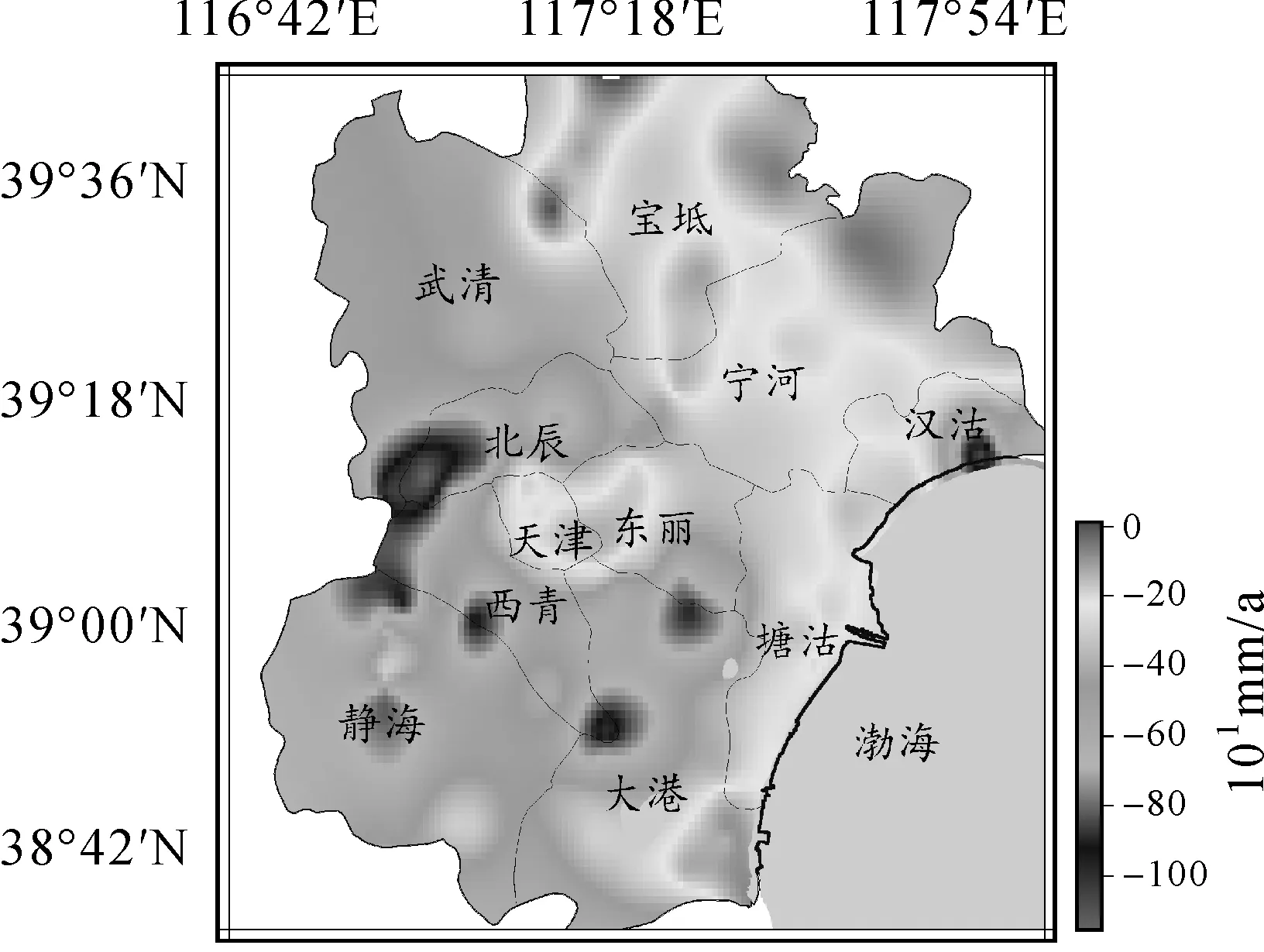
图2 天津市2005—2017年总体沉降量

为了能够更加直观地查看沉降主要区域的时空变化情况，对天津市每年的沉降速率进行求解，如图3所示。

由图3(a)可知，2005—2017年天津市每年都在发生不均匀沉降，呈现漏斗式沉降，大体以北辰、西青、大港、塘沽等为主要区域，且北辰区沉降分布范围逐渐扩大，沉降量逐渐增加。由图3(e)—(g)可知，2009—2011年汉沽地区沉降量逐步增加，2011—2012年汉沽地区沉降量达到最大，速率达到220 mm/a；2012—2016年汉沽地区地面沉降呈现减弱趋势；截至2017年，天津市地面沉降空间分布大体趋于稳定，仅北辰西部与大港中西部仍存在沉降情况。

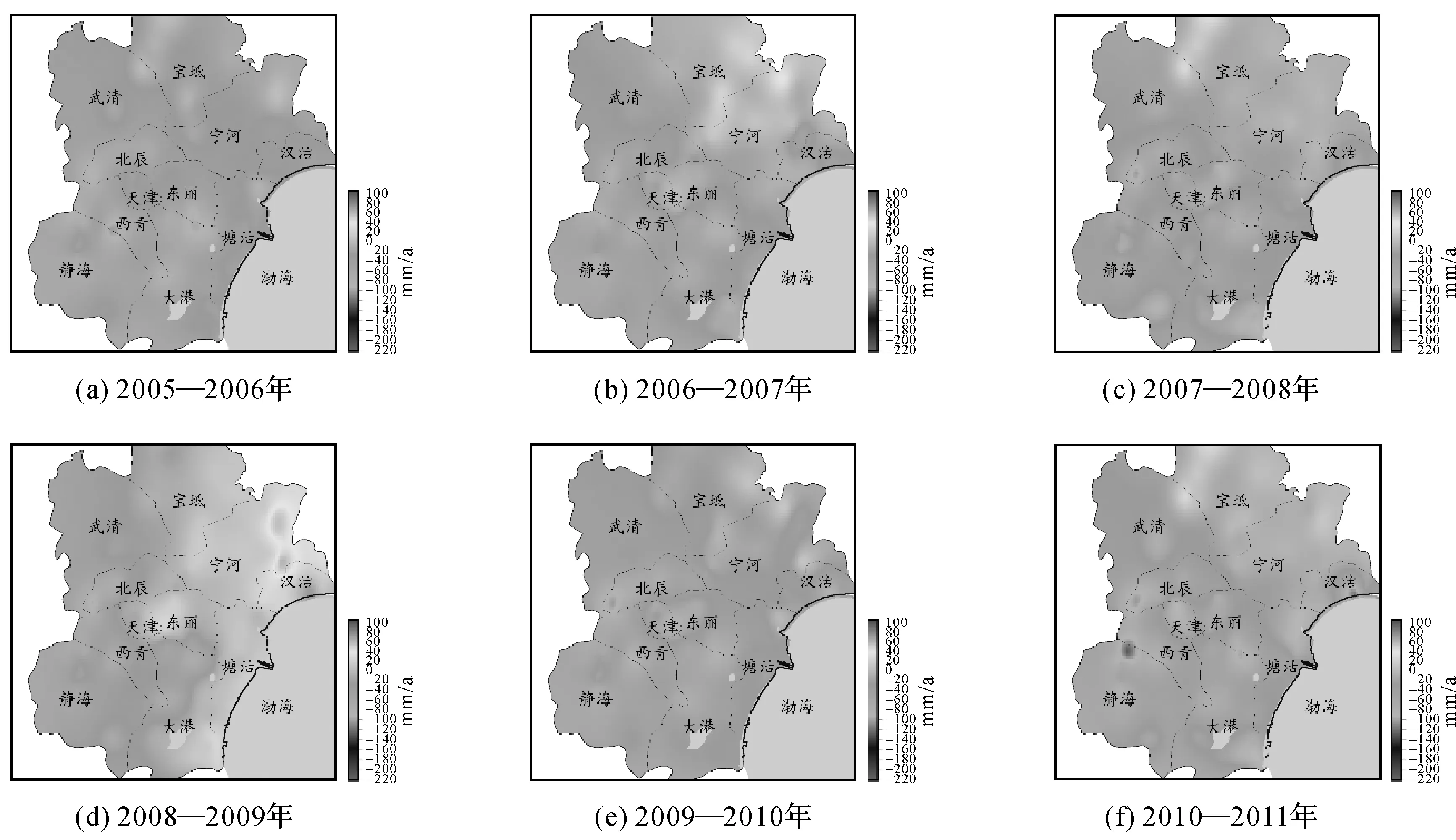
图3 平均形变速率

5 结 语

本文利用天津市2005—2012年、2016—2017年的水准观测数据，以水准点的沉降量、沉降速率、沉降加速率为状态向量，利用卡尔曼滤波算法对水准观测数据进行了处理；并根据得到的结果构建了多项式加权内插模型，对内插结果进行了可视化展示。分析2005年以来天津市地面沉降情况的时空演化特征可对天津市的城市发展及建设提供一定的参考意义。