基于分组粒子群的光伏最大功率点跟踪方法
杨增瑞,孙凤伟 ,戴兆乐,毛明轩
(1.中国电子科技集团公司 第二十八研究所,南京 210007;2.重庆大学 电气工程学院,重庆 400044)
0 引言
太阳能作为清洁再生能源,因其分布广,利用方便,越来越受到人们的关注,并得到广泛的应用。但在光伏发电工程开发中,提高系统的功率转换效率仍然是需要解决的问题之一,其本质上是寻找一种更加有效稳定的MPPT控制方法。通过对光伏发电系统输出特性的分析发现,在复杂遮阴条件下,P-V输出曲线会出现非线性,这将很大程度降低光伏发电系统的功率输出效率。传统的MPPT算法如扰动观察法[1]、电导增量法[2]等因为不能有效的区分局部峰值和全局峰值,而无法实现复杂遮阴情况下的全局最大功率点跟踪。
为了适用于复杂条件下的光伏发电系统的最大功率点跟踪,很多学者提出了改进型算法和智能型算法。其中,文献[3]提出优化后的扰动观察法和全局扫描的方法,实现了全局峰值的搜索。但该方法需要扫描完整的输出P-V曲线,所以收敛速度很慢。文献[4]提出可在线优化的模糊控制器进行光伏最大功率点跟踪控制,该方法能够自适应的进行模糊规则调整。文献[5-6]研究了优化的神经网络控制在MPPT中的应用,虽然神经网络能够有效的解决P-V曲线的非线性特性,但是它们计算复杂,同时受到大量的训练数据的约束,泛化能力较差。其实,MPPT本质为复杂函数的寻优问题,可采用群体智能优化算法,如粒子群算法[7]、人工鱼群算法[8]、人工蜂群算法[9]以及混合蛙跳算法[10]等。其中,粒子群算法因为在处理多峰值、非线性函数的寻优方面有较好的适应性,目前已经被很多学者推广到到光伏发电系统的MPPT控制中。文献[11]作者在传统的粒子群更新方程中引入了额外的关系项,这有助于提高粒子群的搜索能力。文献[12]提出了一种领地粒子群最大功率点追踪算法, 赋予每个粒子领地属性,从而更快的实现遮荫条件下的最大功率点的跟踪。文献[13]研究了一种粒子群优化算法和电导增量法的多峰值MPPT控制,能够较快的实现全局功率点的快速跟踪,并减少稳态输出的扰动。
基于上述研究分析,本文采用基于分组粒子群与优化的扰动观察法相结合方法进行光伏发电系统的MPPT控制,首先通过分组粒子群算法进行快速的近似全局峰值附近收敛,然后采用改进后变步长扰动观察法对全局最大功率点进行动态精确跟踪。最后,通过仿真和硬件实验验证了本文提出方法的有效性,不仅可以实现遮阴条件下的MPPT,而且可以减少输出功率的震荡。
1 光伏电池建模
为了更好的研究光伏发电系统MPPT控制,建立精确而实用的光伏电池模型是十分必要的。在不同的光伏电池模型中,光伏电池单二极管等效电路数学模型[14]被广泛采用,其结构如图1所示。
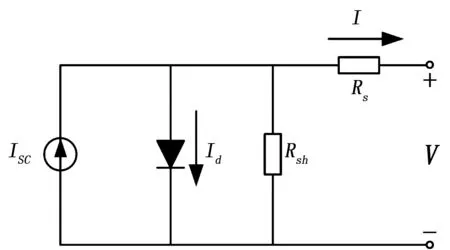
图1 光伏电池组件等效电路模型
图1中,V为光伏电池输出电压,Isc为光生电流,Id为流过二极管的电流,I为光伏电池的输出电流,Rs和Rsh分别为等效串联电阻和并联电阻。根据基尔霍夫电流定律,可以得到光伏电池的I-V方程为:
(1)
式中,I0是反向饱和电流,q是单位电荷,k是玻尔兹曼常量,A是二极管的品质因子,T为绝对温度。
在针对实际工程仿真中,为了方便计算可以采用如下参数模型[15]:
(2)
(3)
(4)
式中,Isc是短路电流,Voc是开路电压,Im是峰值功率点电流,Vm是峰值功率点电压。
2 光伏最大功率跟踪算法
2.1 传统粒子群算法
粒子群算法[8]主要用于解决优化问题,算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个适应度值。该算法的主要思想是:在一个有限空间内,存在不同的粒子,使用Xi=[xi1,xi2, …,xiD]T代表不同粒子的D维坐标位置,同时每个粒子对应一个速度值Vi,并通过自定义目标函数去评判每个粒子的优劣。在每一轮的粒子群迁移过程中,每个粒子都会筛选出个体最优和群体最优分别是Pi=[Pi1,Pi2, …,PiD]T和Pg=[Pg1,Pg2, …,PgD]T。在每轮粒子群的迁移中定义更新粒子坐标位置与速度的公式如下:
(5)
(6)
其中:ω为惯性权重,k为当前迭代次数,c1和c2是粒子加速变量,r1和r2为定义随机数。
2.2 改进粒子群算法
传统PSO算法虽然能够在大多数情况表现出较好的性能,但仍然存在搜索精度不高,易陷入局部最优解等问题。本文对传统PSO算法进行分析改进,使PSO算法更为有效的适用于光伏发电系统MPPT。在相似群体算法中,SFLA因采用的多组群的进化方法,使其拥有良好的全局搜索性能[16]。为解决传统粒子群算法存在的问题,本文将分组思想引入到粒子群算法中,有利于全局最优值的查找和组内粒子位置的更新。由于多了分组操作,同时需要对PSO算法中粒子的更新公式与策略进行调整:
1)分组组内的粒子更新公式为:
(7)
(8)
式中,Pmd表示为第m组内的最优值,m=1, 2, …,M,M为粒子种群分组的个数,n=1, 2, …,N-1,N为每组的粒子个数。
2)组内的最优粒子的更新公式为:
(9)
(10)
式中,Pg表示为种群全局最优值。当组内最优值和全局最优值相近时,式(9)中组内最优粒子的更新速度近似为零,为了避免这种情况的出现,需要在组内最优粒子更新时加入较小的随机的变量。
2.3 变步长扰动观察法
扰动观察法是利用扰动光伏发电系统的输出,进行最大功率点动态跟踪。算法的控制过程如下:设定起始工作电压,一般设定扰动起始电压为开路电压的0.78倍[17],采集光伏发电系统的输出功率,然后以设定值扰动光伏发电系统的输出,获取扰动后的输出功率,若扰动后的输出功率增大,则继续按当前方向扰动,反之,则改变扰动方向。
传统的扰动观察法一般使用固定的步长,但是步长过长容易导致在最大功率点附近较大的波动,而步长较小则会使最大功率跟踪速度较慢。为了解决上述问题,本文采用优化后的变步长算法,进行最大功率附近的功率跟踪。在光伏发电系统的输出功率增大时,输出功率和控制器占空比的特性曲线,即P-D曲线的斜率的变化为先保持稳定然后下降,如图2所示。
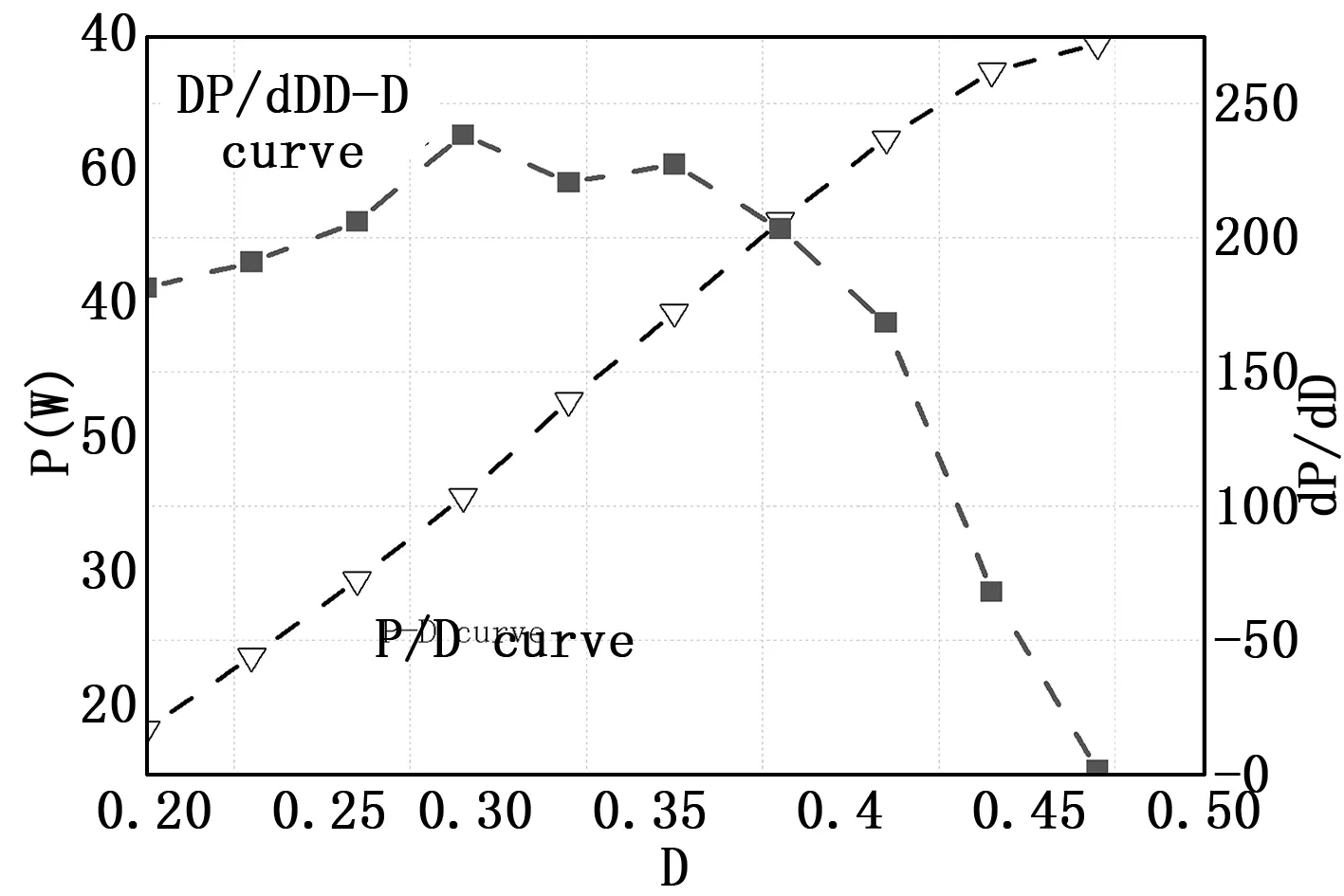
图2 光伏阵列局部P-D输出曲线
依据上述特性,可建立扰动观察法的步长更新公式:
(11)
(12)
式中,α是自适应因子,|dP/dD|max为光伏阵列dP/dD-D曲线的最大值,Dset为扰动的固定步长,Pold和Dold是上一时刻的功率和占空比。
2.4 重启条件
光伏发电系统在外界环境条件发生变化时,先前的全局最大功率点可能变为局部最大值。为此,本文中对光伏发电系统MPPT控制是否需要重新启动进行以下条件判断。首先依据天气条件对光伏发电系统的基本出力影响[18],判断是否光伏阵列出现遮阴情况。当实际输出功率小于光伏发电系统基本出力时,则说明光伏发电系统此时没能全光照条件下工作。
(13)
式中,Preal和Ppv分别为太阳电池组件的实际输出功率和额定功率,G为实际太阳辐射强度;GSTC为标准测试条件下的太阳辐射强度,为1 000 W/m2;αp为太阳电池组件的功率温度系数,取-0.35%/℃;T为太阳电池组件的实际温度;TSTC为标准测试条件下的电池温度,取25 ℃。
在复杂遮阴情况下,当光伏发电系统最大功率点发生偏移改变时,则需要重新开始进行MPPT,根据功率变化设置算法重启的判断,判断条件为:
(14)
式中,Pm为记录的上次最大功率值,ΔP为功率变化比值。
3 MPPT控制策略设计
本文改进的MPPT算法采用分组PSO算法进行光伏发电系统输出功率最大功率点附近的快速收敛,接着,使用变步长扰动观察法继续进行最大功率点的精确跟踪,并在因外界环境变化引起最大功率点偏移时进行MPPT控制的重启。其算法整体流程如图3所示。

图3 本文提出算法流程图
4 实验结果与分析
在验证本文所提出的 MPPT 控制方法时,搭建小型光伏发电系统,其系统电路结构图如图4所示。根据实际光伏板技术参数设置光伏电池仿真模型参数,具体参数为:最大功率为70 W,开路电压43.2 V,开路电流4.5 A,工作电压35.2 V,工作电流3.96 A。此外,电路参数为:电感L=800 μH,输入电容C1=100 μF,输出电容C2=220 μF,负载R=20 Ω。

图4 光伏发电系统结构图
通过对比传统粒子群算法和本文提出分组粒子群算法在不同光照条件下的MPPT的效果,验证本文提出算法在光伏系统最大功率点跟踪应用中的实用性和优越性。通过对光伏板设置不同光照强度来模拟光伏发电系统复杂的遮阴条件,在本文实验过程中,将2块光伏板中的一块光照强度由1 000 W/m2改为700 W/m2。光伏发电系统工作在两种不同条件下的输出特性曲线如5所示。
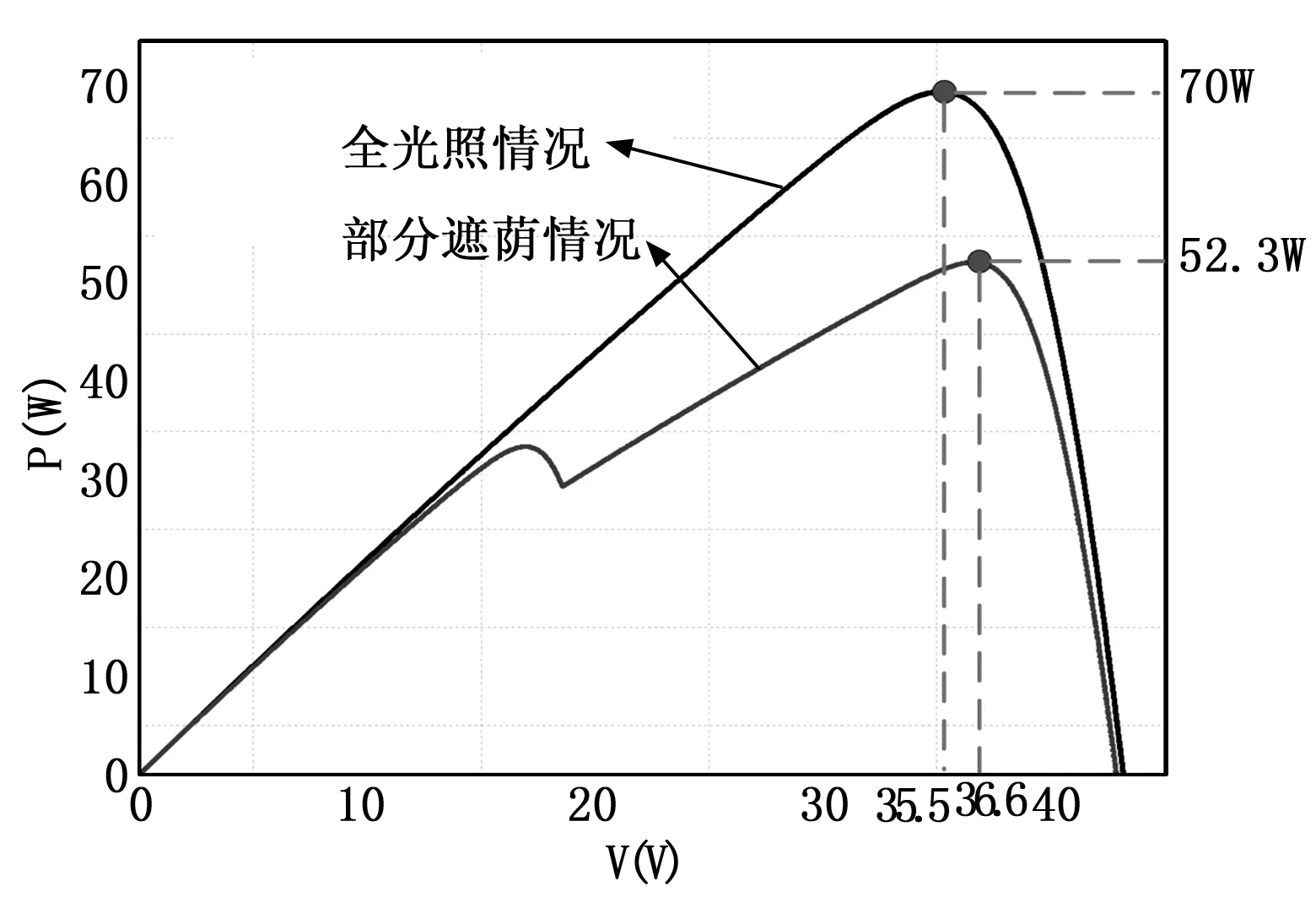
图5 不同条件下的光伏阵列P-V曲线
4.1 仿真实验结果
根据对实际光伏发电系统的实验分析,对不同PSO需要设定不同的初始参数,针对本文实验对比的两种PSO算法具体参数设定如表1。
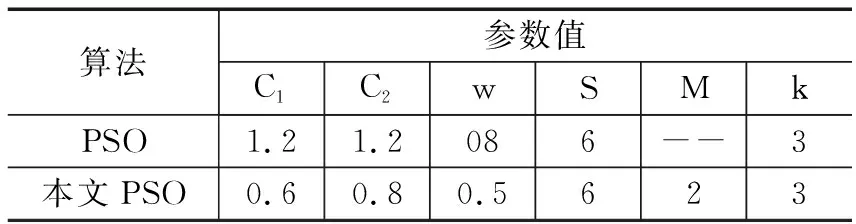
表1 算法基本参数
首先,采用传统的PSO算法进行MPPT控制仿真实验,仿真输出功率曲线和光伏发电系统控制器的占空比变化如图6所示。传统粒子群算法粒子收敛变化对参数依赖较大,粒子更新过程存在很大的不确定性。分析输出功率曲线发现,在粒子收敛过程中,功率输出震荡幅度较大,在实际工程中这会整个发电系统造成不稳定性。通过较长时间的搜索,在标准光照条件下,传统PSO算法的粒子收敛在0.481附近,此时光伏系统的输出功率为69.6 W,与标准理论值相差0.4 W,相对误差为0.57%。在设定的模拟遮阴情况下,MPPT的结果是粒子收敛值为0.39,输出功率为52.1 W,相对误差值为0.38%。整体上,传统粒子群算法能够进行光伏发电系统的最大功率点跟踪,但是存在收敛速度慢,搜索过程震荡大等问题。
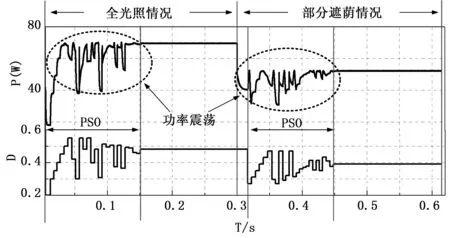
图6 传统PSO算法仿真结果
为了解决上述传统PSO算法在光伏系统MPPT控制的问题,采用本文提出的分组PSO算法和变步长扰动观察法组合的MPPT方法进行仿真实验,实验曲线如图7所示。与图6结果比较可知,本文提出MPPT方法具有更好的性能,具有更快的搜索速度和稳定的功率输出。在标准光照条件下,提出分组PSO的粒子值收敛在0.462,搜索的最大功率点值为69.9 W,与标准理论值仅相差0.1 W,相对误差为0.14%。在遮阴重启后,粒子最终收敛为0.383,输出功率为52.3 W,与理论值相同。
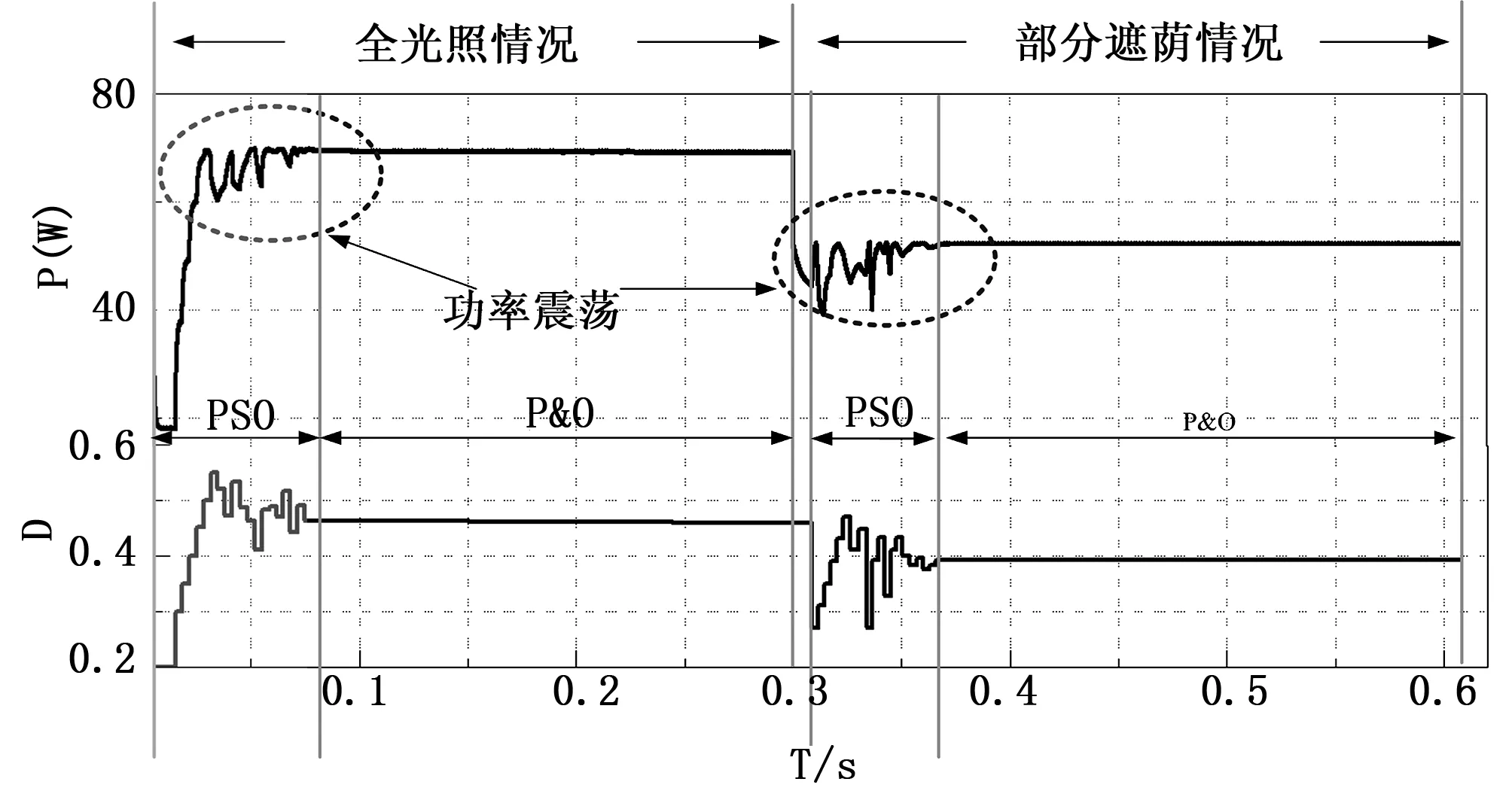
图7 本文MPPT算法仿真结果
4.2 硬件测试结果
进一步在硬件实验平台上对本文提出方法的工程可行性进行验证,根据系统模型搭建实验硬件平台,实物如8所示。

图8 光伏硬件测试平台
在测试当日的环境下,无遮挡时,光伏发电系统的开路电压为40.9 V,短路电流为0.68 A。测试中,同样进行两种不同场景下的MPPT控制实验,并通过示波器记录实验结果如图9和图10所示,图中,横坐标为时间,每格为0.5 s,纵坐标为电压值,每格为10 V。
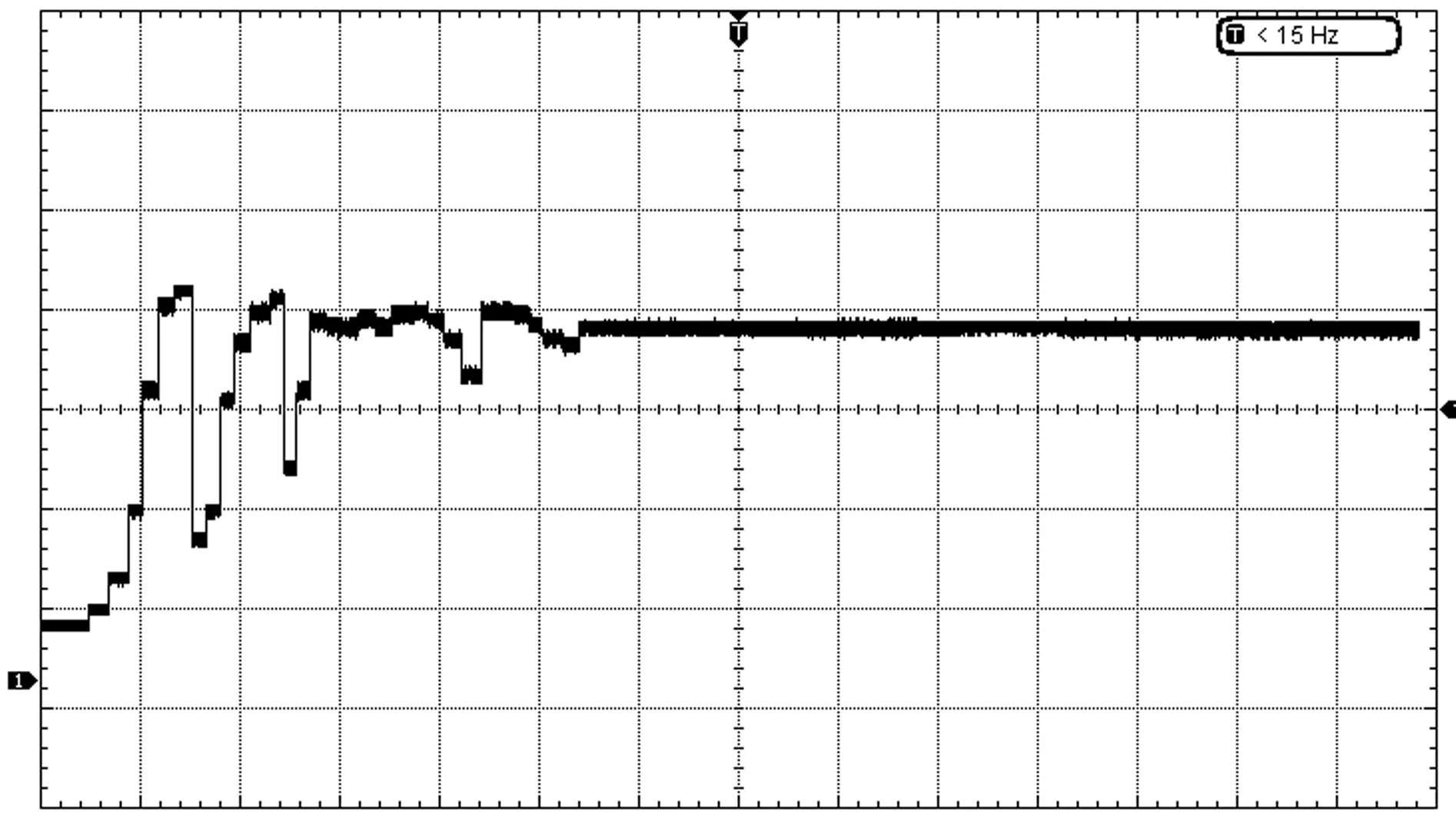
图9 全光照条件下实验波形
其中,图9为光伏板在未遮挡情况下进行MPPT控制时电压输出曲线,经过大约2 s的搜索后,光伏板的输出电压稳定在35.2 V附近,系统输出功率为21.2 W。图10是光伏发电系统其中一个光伏板局部遮挡时的电压输出曲线,此时电压最终稳定在27.3 V附近,输出功率为16.4 W。

图10遮阴条件下实验波形
5 结束语
通过对光伏发电系统在复杂遮阴条件下的输出特性曲线进行分析,提出一种改进PSO结合变步长扰动观察法的MPPT控制方法。通过将分组策略引入传统PSO算法中,提高算法的收敛速度和稳定性。同时,改进的变步长的扰动观察法,精确跟踪算法重启间歇环境渐变引起的功率渐变,同时有利于减少计算量。通过在不同光照条件下的仿真和硬件平台实验表明该方法能够快速的搜索光伏发电系统功率输出的全局最优,高效的进行光伏最大功率点的跟踪,并可以有效的降低MPPT控制过程中的输出波动,进一步提升光伏发电系统的发电效率。
——中国制药企业十佳品牌

