基于卷积神经网络的通信信号调制识别研究
杨 洁, 夏 卉
(西安邮电大学 通信与信息工程学院, 西安 710121)
0 引言
自动调制识别(automatic modulation recognition,AMR)是一种在不知道接收信号调制类型的情况下,自动对信号调制类型进行分类的过程,AMR在民用和军事实际应用中发挥着重要作用[1]。AMR算法可以分为两类:基于似然(likelihood-based,LB)的方法和基于特征(feature-based,FB)的方法。LB方法利用概率论、假设检验理论和决策准则等来解决信号调制识别问题,虽然LB方法可以获得最佳结果,但是计算复杂度很高。FB方法从接收信号中提取若干特征然后用分类器进行识别分类,其中提取的特征包括基于瞬时特征[2]、高阶累计量[3]、循环谱技术[4]、时频分析[5]等,在分类过程中,分类器主要包括决策树[6]、支持向量机[7]、人工神经网络[8]等,FB方法大大降低了计算复杂度。但不论是LB方法还是FB方法都需要大量的先验知识支撑,只适用于特定信号的识别,局限性较大。
针对以上问题深度学习方法被用于自动调制识别。Ao Dai等人[9]使用堆叠稀疏自动编码器,提出从信号的模糊函数提取特征的方法,S.Jeong等人[10]研究通过短时傅里叶变换生成频谱图和卷积神经网络(convolutional neural network, CNN)模型结合的方法进行识别,李永乐等人[11]研究了一种通过循环谱图和CNN模型结合的调制识别方法。以上方法缺点是在低信噪比情况下识别率仍然很低。
基于上述分析,本文研究了一种复基带信号与CNN结合的方法,并提出了CNN模型,这种方法直接从数据中自动学习信号特征。该模型首先仿真生成不同信噪比下的七类调制信号,然后将接收到的信号处理为复基带IQ两路信号,对信号进行预处理后作为实验的数据集,用该数据集来训练CNN模型、调整超参数,最后利用训练好的CNN模型对七类通信信号就行识别分类。实验表明,本文提出的方法在低信噪比情况下有较好的分类准确度,且较文献[10]中短时傅里叶变换后利用卷积神经网络进行分类识别的方法准确度有较大提升。
1 信号调制模型
基本的数字调制方式有如下3种:多进制频移键控(multi-band frequency shift keying,MFSK)、多进制振幅键控(multi-band amplitude shift keying,MASK)和多进制相移键控(multi-band phase shift keying,MPSK)[12]。3种信号可数学建模如下:
(1)
(2)
(3)

在此基础上,多进制正交调制(multi-band quadrature amplitude modulation,MQAM)同时利用了载波的振幅与相位对传输数据进行调制。MQAM表达式:
(4)
由(1)、(2)、(3)和(4)可得调制信号的一般表达式为:
s(t)=A(t)·cos[2πfct+2πf(t)t+θ(t)+θ0]
(5)
其中:s(t)表示连续时间序列信号。根据公式(5),改变其频率、相位、振幅或其他参数得到七种调制模型。
2 数据集的生成及预处理
采用数字下变频(digital down converter,DDC)对公式(5)得到的信号进行处理,得到包括同相分量与正交分量两部分的复基带信号,其一般表达式为:
I(n)=A(n)sin(ω0n+nω(n)+φ(n)+φ0)
Q(n)=A(n)cos(w0n+nω(n)+φ(n)+φ0)
(6)
其中:I(n)表示调制信号的同相分量,Q(n)表示调制信号的正交分量。经过信道后,接收信号y(n)可以描述为:
(7)
其中:Ci与ki代表子路径增益与延迟;fi为多普勒频率;v(n)表示加性高斯白噪声(additive white gaussian noise,AWGN)。
在现实中除了存在信道噪声,调制信号识别的准确性还会受到码间串扰(inter-symbol interface,ISI)和频率偏移等因素的影响。由于信道中存在码间串扰,为了消除码间串扰对识别准确率的影响,根据奈奎斯特准则,采用升余弦滤波器(raised cosine transmit filter,RCTF )来消除码间串扰,使每个复值信号经过一个滚降系数为0.4的升余弦滤波器。升余弦滤波器的冲激响应如下:
(8)
其中:α为升余弦滤波器的滚降系数,f0为滤波器的带宽。
综上所述,本文考虑在AWGN信道条件下,输入数据集预处理的过程如图1。

图1 数据集生成原理图
调制识别是将接收到的通信信号的调制类型分类,这是一个n类决策问题。通过根升余弦滤波器后,得到2×N的二维向量矩阵作为输入的数据集,其中矩阵的第一行是复基带信号的同向分量,第二行是复基带信号的正交分量。
3 基于卷积神经网络的调制识别方式工作原理
3.1 卷积神经网络的结构
利用卷积神经网络结构进行调制识别的过程,首先是将预处理过的7类调制信号分别处理为训练集和测试集,然后通过训练集训练CNN模型,并对CNN模型的超参数进行微调,训练完成后通过输入测试集对CNN模型进行测试,最后对数字通信信号进行识别分类。
卷积神经网络是由卷积层、池化层和全连接层组成的前向反馈的多层神经网络[13]。卷积神经网络中每层的神经元从输入的数据中自动进行特征提取特征,从而更新每层神经元的权值。神经元的工作原理如图2所示,由n个输入向量[x1,x2,...,xn]与其对应的权重向量[w1,w2,...,wn]作内积,并加上偏倚b,再经过非线性激活函数h(∑iwixi+b)得到输出f(x;w,b)。卷积神经网络具有局部感知和权值共享的特点,可以降低训练参数的个数,减少了计算复杂度。

图2 神经元的工作原理
1)卷积层是对输入的数据进行特征提取。输入的数据一般是特征矩阵,每个卷积层的卷积核尺寸和移动的步长由人工设定,通过卷积核和上一层的特征矩阵进行卷积运算,每计算一个数据窗口后,卷积核平移到下一个位置,通过激活函数得到输出的特征矩阵。卷积层的计算公式:
(9)
其中:l为网络层数,f(·)为激活函数,x为输入向量矩阵,k为卷积核矩阵,b为偏倚量,Y为输出矩阵,j为特征图数量。
2)池化层可以有效的缩小矩阵尺寸和纬度,进一步减少全连接层中的参数。池化层前向传播过程与卷积层类似,需要人工指定滑动窗口矩阵的大小和步长,本文中池化层采用每滑动一次窗口取最大值作为输出,输出也是三维矩阵的形式。
(10)
其中:x为池化层中输入特征的矩阵,N×M为池化滑动窗口的大小。
3)全连接层将所有的神经元与上一层的所有神经元相连,输出1×N的二维矩阵形式。由于经过全连接层后输出的维度与原输入的维度不同,所以最后需要与Softmax相连,对于指定类别的样本,最终计算得到每个类别的概率。Softmax回归将样本x(i)标记为类别j的概率为:
(11)
Softmax交叉熵损失函数为:
(12)
其中:y(i)为one-hot编码形式,若y(i)=j为真,则I{·}=1,反之I{·}=0,k为类别,M为样本数。
在训练神经网络时,为了使交叉熵损失函数值最小,使用适配性矩估计(Adaptive Moment, Adam)优化算法更新权值。Adam同时具有动量算法(Momentum)和均方根传播算法(Root Mean Square Propagation,RMSProp)的优点,通过计算损失函数的一阶矩估计和二阶矩估计为不同参数独立的自适应性学习率,快速得到全局最优解,具体步骤如下。
步骤1:初始化损失函数梯度的一阶矩估计mw=0、损失函数梯度的二阶矩估计vw=0、迭代次数t=0,训练集D={x(i),y(i)},i=1,2,...,N。
步骤2:更新迭代次数t←t+1;
步骤3:随机从训练集D中取M个子集,得到Dm,
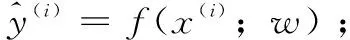
步骤4:计算损失函数的梯度▽L。
(13)

(14)
(15)

(16)
其中,β1β2为加权指数,取β1=0.9,β2=0.999,η为学习率在训练过程中进行微调,ε为平滑因子,ε=10-8。
步骤7:重新返回步骤2,继续训练下去。直至达到停止条件。
3.2 CNN-IQ卷积神经网络模型
本文提出一种卷积神经网络模型,命名为CNN-IQ。CNN的模型框架图如图3所示,由1个输入层(Input)、2个卷积层(Convolution,Conv),2个最大池化层(Maxpool),1个全连接层(Fully connected,Fc)和1个Softmax分类器组成,最后将7种信号的调制类型输出,模型参数见表1。

表1 CNN-IQ模型参数

图3 CNN-IQ模型
输入层输入的是2×1 024大小的2维矩阵;Conv1卷积核大小为1×2、深度为256、步长为1×1,使用全零填充,经卷积计算得到256个2×1 024的特征图,本层总共有2×512×256×(1×2+1)=786 432个连接。Maxpool1滑动窗口大小为1×2、步长为1×2、使用全零填充,得到256个2×512的特征图。Conv2中卷积核大小为2×2、深度为128、步长为1×1,不使用全零填充,两个卷积层使用线性整流函数(Rectified Linear Unit, ReLU)作为激活函数,激活函数使得整个神经网络模型为非线性,经卷积计算得到256个1×511的特征图,本层共有1×511×256×(2×2+1)=654 080个连接。Maxpool1滑动窗口大小为1×2,步长为1×1,使用全零填充,得到128个1×128的特征图。全连接层一共由256个神经元组成,全连接层共有1×128×128×256+256=418 456 0个连接。最后,Softmax层输出节点的个数为7个。为了避免过拟合,在全连接层处设置p=0.5丢失输出(Dropout),Dropout方法可以随机删掉网络中一半的神经元,同时保持输入输出的神经元不变,可以进一步提升模型可靠性并防止过拟合。
4 仿真实验和结果分析
4.1 实验数据集准备
为了训练卷积神经网络模型,需要大量的训练集和测试集样本数据集,在实验中利用Matlab产生了7种数字信号模型的IQ数据包括:2FSK、4FSK、BPSK、8PSK、QPSK、QAM16和QAM64。数据集中每类信号由1 024个样本点组成,保存为2×1 024的矩阵格式,矩阵的第一行为I路信号第二行Q路信号,数据集的具体划分情况如表1所示。数据集的信噪比由-10 dB到18 db,间隔为2。产生信号的参数:采样频率为1 000 Hz,载波频率为100 Hz,码元数目为256。其中训练集包括49 000个样本,测试集包括4 200个样本。信号样本标签采用one-hot编码格式。

表2 数据集具体划分情况
实验环境如下:显卡为TITAN X GPU、处理器为Intel(R) Xeon(R) CPU E5-2620 v3 @ 2.40 GHz,内存为10 GB。软件环境:数据集在window 10下的MATLAB 2016 b下生成,卷积神经网络的训练在Ubuntu系统下使用tensorflow1.12框架搭建,开发语言为Python3.6。
4.2 实验结果分析
实验中,学习率从0.001开始训练框架CNN-IQ,在训练中测试集的损失值大于此时的最大损失值时,让此时的学习率乘以0.02来进行修正学习率。实验中共训练100轮次,每轮次时间约23秒,图4为训练损失值与验证损失值和训练轮次的曲线图。训练损失和验证损失值随着轮次的增加,损失值均迅速下降,逐渐两条曲线趋于一致,说明本实验模型没有出现过拟合的现象。epochs=38后损失值基本稳定,并且训练损失和验证损失两条曲线均收敛,epochs=100时,验证损失值为0.035,此时的损失值已经达到最小值,训练结束后,将训练好的卷积神经网络模型框架和权值保存,方便CNN-IQ模型进行迁移训练。

图4 训练损失和验证损失随训练次数的变化
对训练好的CNN-IQ模型使用7类通信信号的测试集进行验证。图5为CNN-IQ模型7种调制信号平均识别准确率随SNR变化的曲线。分析识别结果可以发现:随着SNR的增加,7种信号的平均识别准确率上升,当信噪比为-4 db时,BPSK、2FSK和4FSK识别率均为99%以上。当在信噪比为18 db时,7种信号的总平均准确率可以达到98.85%。

图5 不同信噪比下的信号识别准确率
图6为不同信噪比下的混淆矩阵,混淆矩阵对角线上的颜色越深,代表识别准确率越高。图6(a)为CNN-IQ模型SNR=18 db时测试集的混淆矩阵图,图6(b)是SNR=0 dB时的混淆矩阵图。当SNR=18 db时,除64QAM识别准确率为95%外,其余6种调制信号的准确率都达到99%以上。当SNR=0 db时,7种调制信号的准确率都达到90%以上。
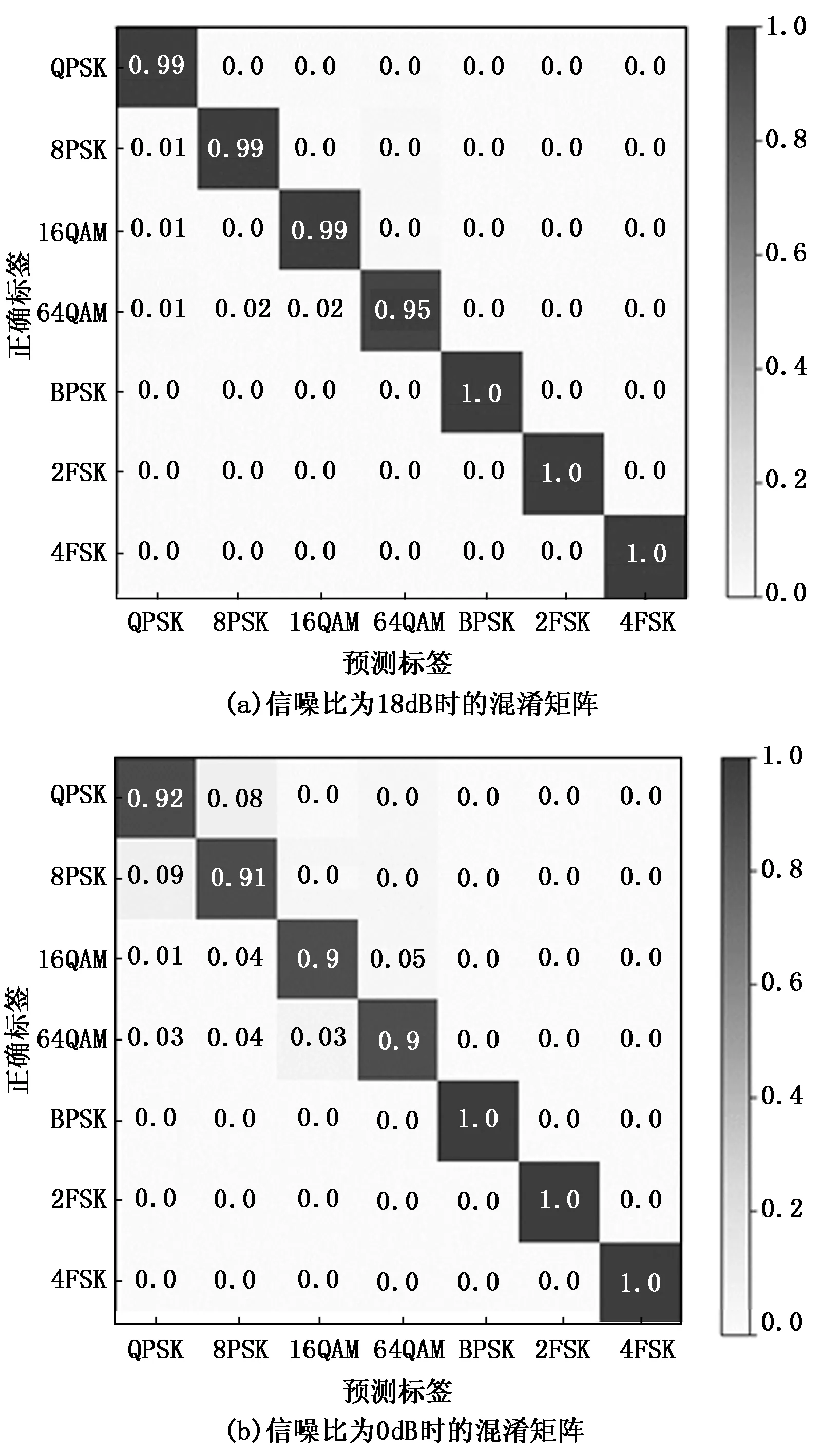
图6 不同信噪比下的混淆矩阵
为了评估框架的识别性能,在相同数据集下,通过将文献[10]的方法与本文方法CNN-IQ进行比较,分析了两种方法随信噪比的升高对识别准确率造成的影响。

图7 两种方法在不同信噪比下的信号平均识别准确率
由图7分析得出,当信噪比较低时,本文方法较文献[10]的方法准确率有极大提升。从图7中的分析结果可以看出,在信噪比小于0 db时,本文方法将准确率提高25.41%左右。当信噪比等于0 dB时,本文平均准确率达到94.61%,而文献[10]的方法平均准确率为72.13%。当信噪比为18 db时,本文方法准确率达到98.85%,而文献[10]方法,准确率为95.32%。与文献[10]提出的方法比较分析得出,CNN-IQ在较低信噪比下准确率有较大幅度的提升,在信噪比较高时准确率也有一定程度的提升。
5 结束语
对于数字通信信号的识别,本文提出一种基于复基带信号的卷积神经网络调制识别方法。首先给出了将生成的数字信号处理成为复信号的方法,然后将数据预处理,利用生成好的数据集对搭建的卷积神经网络进行训练,通过不断调整卷积神经网络的超参数使得损失值最低且收敛,提出一种CNN-IQ模型,最后利用CNN-IQ模型进行迁移学习来识别七类数字通信信号。仿真结果表明,本文方法对数字通信信号识别方法有效,并且在信噪比较低的情况下,信号识别的准确率有大幅度提升。下一步考虑双通道卷积神经网络,对如何减少卷积神经网络结构和参数,同时能保持较高的识别准确率进行研究,进一步提升整个识别过程的运行速度。

