基于系统非线性因素的阵风载荷减缓技术研究
杨建忠,秦先学,杨士斌,徐 丹
(中国民航大学 天津市民用航空器适航与维修重点实验室,天津 300300)
0 引言
气动伺服弹性是一门涉及空气动力学、结构动力学和控制理论的交叉学科,目前在航空领域与该学科有密切关联的研究为颤振主动抑制和阵风减缓[1-2]。而随着现代大型民机的柔性不断增加,导致阵风载荷的危害剧增,使得阵风载荷的主动抑制研究成为一种新的趋势[2]。
对于阵风载荷减缓技术而言,国内外学者目前主要是利用反馈控制进行阵风载荷减缓研究:有基于奇异值控制理论,去分析系统的鲁棒性[3],或利用二元机翼模型进行自适应控制,分析最大控制面偏转对阵风载荷的影响[4],或采用μ综合控制进行多舵面控制研究等[5]。
而基于加速度反馈的传统控制策略对系统未来动态缺乏了解,其控制效能也有限,从而导致对作动系统指标要求苛刻,需要过高的舵偏行程与舵偏速率,以及过低的系统延迟[6]。而随着机载探测设备地不断进步更新,可以利用机载探测设备进行测量,以提供飞机前方阵风场的精确速度信息,从而更新阵风减缓系统的布局形式,以达到更好的阵风减缓效果[7]。
国内外部分学者通过利用机载激光雷达,预测前方阵风信息,有采用前馈控制[8],或最优控制策略[9],或基于模型预测控制[10]等方法,进行阵风载荷主动减缓技术研究。然而,提前获取前方阵风信息的需求是源于实际工程中的系统非线性因素限制,但国内外大多数研究,都尚未充分结合新的阵风感知方式,去考虑实际工程中的系统非线性因素所带的影响。
目前,针对国内外阵风减缓问题而言,对具有工程意义的气动弹性系统的非线性因素问题以及基于新的感知方式的控制方案的研究较少,缺乏控制方案与非线性系统因素相结合的具体模型研究。
因此,本文考虑新的阵风感知方式,去预测飞机前方阵风的速度信息,并通过总结实际工程中的控制作动方式所带来的系统非线性因素,研究其来源及注入方法,分析其对阵风减缓的影响。最终,建立包含阵风激励的气动伺服弹性模型,并利用自适应前馈控制的方案,来研究新的感知方式对载荷减缓系统这类高动态响应系统的影响。
1 阵风载荷减缓系统
1.1 飞机气动弹性建模
本文采用了通用运输机模型(general transport aircraft,GTA)[11],该模型普遍应用于民机的算例分析以及控制方案等研究。飞机具体参数如下:质量7 210.85 kg,机身长度22.1 m,高度6.0 m,机翼翼展19.1 m,机翼弦长2.42 m。利用有限元方法与偶极子网格法,计算得到全机的结构有限元模型和气动模型,分别如图1和图2所示。其中,结构模型含有141个结构单元和121个节点,气动模型含有872个偶极子(DLM)网格。并采用样条插值法对两个全机模型进行耦合,可得到该通用运输机的气动弹性模型。

图1 GTA结构有限元模型

图2 GTA气动模型
其基于广义坐标的气动弹性方程为[12]:
(1)
式中,q为飞机弹性模态与刚体模态坐标,δ为操纵面偏转模态坐标,Mqq和Mqc为模态质量矩阵,Dqq为模态阻尼矩阵,Kqq为模态刚度矩阵,q∞为飞机前方的来流动压,wg(t)为垂直阵风的速度,V为飞机的飞行速度,Qqq、Qqc和Qg分别为飞机模态、控制面模态和阵风模态的气动力系数矩阵。
为了简化方程,这里采用最小状态法(MS)[13],对上述方程进行非定常气动力的有理近似化,进而可获得弹性飞机在阵风激励下的运动方程:
(2)
1.2 阵风模型
对于离散阵风,采用“1-cos”形式,由CCAR25.341规定离散阵风的数学模型为:
(3)
式中,s为进入阵风区的距离,Uds为设计突风速度,H为阵风梯度。
而对于连续湍流,选用湍流尺度为2 500英尺的VonKarman功率谱模型,如下式所示:
(4)
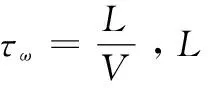
1.3 阵风载荷减缓线性系统模型
通常,传统的阵风载荷减缓系统(GLAS)主要由传感器、控制器、作动器(包含操纵面)与受控对象组成。其基本原理是:飞机在遭遇阵风时,在飞行控制系统的基础上,通过传感器实时测量阵风载荷并将其各项参数指标反馈给控制器,随后,控制器输出指令信号,驱动作动器进行控制面偏转,以达到阵风载荷减缓的效果,其系统原理模型如图3所示。

图3 阵风载荷减缓系统
1.4 传统PID反馈控制分析
对比模型的控制器选用传统的PID负反馈控制,同时加入低通与陷波滤波器以降低机身弯曲模态的影响。其中,控制舵面选用副翼,利用对称偏转来减小由垂直阵风引起的阵风载荷。离散阵风下,其不考虑系统非线性因素时的翼尖加速度阵风响应曲线如图4所示,虚线表示理想线性系统的开环响应曲线,实线表示理想线性系统在PID负反馈控制下的闭环响应曲线。从中可以看出阵风响应的翼尖加速度在传统的PID负反馈控制作用下减缓效果较为明显,其闭环系统的阵风响应过程是先在离散阵风激励下达到响应峰值,而后穿逐步衰减振荡,最后趋于稳态。

图4 不考虑非线性因素的翼尖加速度响应曲线
2 系统的非线性因素分析
2.1 阵风减缓系统非线性因素
而在实际工程中,在原有的理想阵风减缓模型的基础上,还存在系统的非线性因素,从而使系统展现出不同的特性,其中主要包括舵面偏转行程饱和、舵面偏转速率限制以及系统延迟所导致的系统非线性因素[14]。实际中,这3种系统非线性因素会严重影响阵风载荷减缓的功能[14],在设计模型中如果不全面考虑其影响性,甚至会引发其功能的完全失效。其非线性特性曲线,如图5所示。

图5 系统非线性特性
舵面偏转行程与作动器的特性有关,并且由于阵风载荷减缓系统属于飞控系统的子系统,前者与后者是采用相同的飞机舵面作为控制面。而为保证飞机正常的飞行机动能力,前者的控制权限是受制于后者的,从而致使阵风载荷减缓系统的控制面偏转受限的情况出现。
在对舵面偏转行程受限进行分析时,可直接在作动器模型前,对输入的指令信号增加饱和环节,以达到作动器偏转行程受限的效果。其注入的饱和环节的数学模型如下:
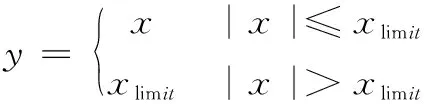
(5)
其中:x为饱和环节的输入,y为饱和环节的输出,xlimit为幅值限制值。
舵面偏转速率是由作动器的特性决定,而作动速率是有限值。通常,系统会对其速率进行限制,以避免过度指令对系统造成负面影响。对于舵面偏转速率限制而言,本身是包含于作动器的自有属性。因此,在建立作动器模型时,可在模型中注入速率限制环节,以达到舵偏速率受限的目的。其速率限制环节的数学模型如下:
(6)
式中,R为操纵面偏转速率,RL为速率限制值,u(i)、δ(i)为速率限制环节的输入和输出。
系统延迟是指信号在传输过程中的时间滞后特性,主要包括传感器对数据测量的时间延迟和控制器带来的控制延迟。在系统模型中的可综合叠加表现为控制器输出信号的时间延迟,其注入方式可在控制器后加入延迟环节,其数学模型如下:
x2(t)=x1(t+Δt)
(7)
2.2 阵风减缓系统非线性因素影响分析
为了更好地展示系统非线性因素对阵风载荷减缓的影响,针对系统中的舵面偏转行程饱和、速率限制(即速率饱和)与延迟3种特性,分别在不同特性情况下,与开环、闭环线性的输出响应进行减缓效果对比分析。
从图中可以看出,在上述的系统非线性因素的影响下,其翼根弯矩的响应峰值迅速增大;其中,舵偏行程饱和相比于速率饱和,对最大翼根弯矩减缓影响更大;对比于闭环线性曲线,其快速性和稳定性都明显下降,阵风减缓效果下降也较为明显;且饱和特性的响应曲线存在明显的滞后性。

图6 饱和特性下翼根弯矩归一化结果
同样情况下,考虑系统延迟的非线性因素,选取不同的延迟时间,其数值分别为t1、t2、t3,量值依次增大,其延迟特性下翼根弯矩的响应曲线,如图7所示。从图中可以看出,系统非线性因素的延迟时间越大,系统对最大翼根弯矩的响应峰值越高,意味着其减缓效果变差。此外,从曲线整体上看,延迟对系统的稳定性存在重大影响,延迟的增大使系统趋于震荡发散状态,这导致阵风减缓效果大大降低,甚至使系统处于失效状态。

图7 延迟特性下翼根弯矩归一化结果
由此可知,上述的系统非线性因素对飞机阵风载荷减缓影响显著,其减缓效果与控制面偏转的最大限制紧密关联,而延迟对系统稳定性更是存在重大影响。随着上述非线性限制因素的不断放宽,其载荷减缓效果指标也不断趋于理想的闭环系统状况。因此,对于阵风减缓系统而言,上述系统非线性因素是需要重点考虑的对象。
3 阵风预测与自适应前馈控制方案
为了解决传统反馈控制以及上述系统非线性因素所带来的问题,本文选取新的阵风感知方式,采用机载测风雷达提预测飞机前方的阵风信息,并选用基于FIR滤波器结构的前馈自适应控制,实时输出控制面偏转指令,将上述系统非线性因素结合到控制方案中,充分考虑阵风减缓系统的实际工程状况。
3.1 阵风预测技术
机载激光测风雷达是以激光为光源向大气发射激光脉冲,在接收大气粒子的后向散射信号后,通过分析激光的多普勒频移来计算出径向风速。通常,可利用多束光波得到多维的径向风速,从而计算出飞行路径上的垂直阵风速度。本文采用二维探测模型进行估算[15],其原理图如下:

图8 机载激光雷达阵风探测
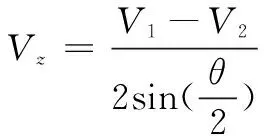
(8)
式中,Vz指Z方向上的阵风速度,V1和V2分别指两束光波方向的径向阵风速度,θ指两束光波之间的夹角。
由于大气阵风速度在时间和空间上变化,激光雷达径向速度测量值不是在相同的位置进行的,并且两个测量都不在飞行路径上。此时,会产生额外的误差,由此可计算出其垂直阵风速度的总标准差为:
(9)
式中,σtotal指总的阵风垂直速度标准差,σz指不考虑大气阵风速度在时间和空间上变化的Z方向上的速度标准差,D(z)指大气结构函数,约为2倍大气阵风速度标准差[16]。
通过机载激光雷达对前视阵风信息的探测,可获取测量点的垂直阵风数据,根据上述模型可获取垂直阵风的速度以及标准差信息,从而准确预测飞机前方的垂直阵风速度场,为阵风减缓控制器提前提供有效的阵风值输入。
3.2 有限脉冲响应(FIR)数字滤波器
通常,实现自适应前馈控制可利用数字滤波器系数不断更新的方式去实现。其具有可编程和适应性好的优点,并且对相位和延迟控制精确,十分有利于解决系统非线性因素所带来的影响。而现有的数字滤波器主要有两种:有限冲击响应(finite impulse response,FIR)滤波器和无限冲击响应(infinite impulse response,IIR)滤波器。前者相比于后者,具有较好的稳定性。由于不会产生新的非零极点,FIR能在阵风减缓控制过程中,始终保持着控制器的稳定性[17]。因此,FIR结构的数字滤波器更适合作为自适应前馈控制器的基础结构。

图9 FIR数字滤波器的原理构造
其FIR数字滤波器构造图,如图9所示,根据其原理可得其下列关系式:
(10)
式中,uFF指控制面偏转指令信号,h指滤波器系数,α指垂直阵风速度信息的离散信号,N指滤波器长度,即抽头数。
3.3 自适应前馈控制方案
基于风扰动信息以实现阵风自适应减缓控制的框架,重点在于提前获取并预测飞机前方的阵风信息,并利用阵风模拟预测值来设计前馈控制器。因此,采用自适应的方式的本质是利用飞机传感器反馈的阵风载荷信息,实时更新FIR滤波器的冲击响应序列,从而不断改变FIR滤波器的各个系数。最终,输出控制面偏转命令量uFF,驱动作动器进行舵面偏转。其自适应前馈控制原理图,如图10所示。

图10 自适应前馈控制原理图
以翼根弯矩为减缓目标,以误差信号为减缓指标,其中,误差信号为质心加速度与翼尖加速度之差,包含其分为两部分影响,一部分为大气扰动量引起的误差信号量,另一部分为控制面偏转导致的误差信号量[17]。通过弹性飞机模型反馈的阵风响应信息,采用逆梯度方式对滤波器系数进行自适应收敛更新,其系数迭代公式如下[17-18]:
h(n+1)=h(n)-c·e(n)r(n)
(11)
式中,h为滤波器的系数,c为收敛系数,e为误差信号,r为前馈滤波器的参考信号,n为迭代次数。
此外,为了更好地考虑系统的非线性因素,结合前馈控制,可引入一个时间参数变量t,使得控制命令提前发出,以达到前馈补偿作用,其量值主要由以下两点因素决定[18]:1)依据机载测风雷达的测量距离与飞机当前飞行速度对比,计算出飞机提前获取阵风信息的最快时间T1。2)依据作动器的动态特性、控制面偏转速率限制和系统延迟等可以计算得到从当前控制面位置偏转到信号指令要求的控制面位置所用的时间T2。根据T1与T2参数值,适当选取前馈补偿算法的提前作用时间参数t,可以使得系统达到阵风减缓的最大效果。
该方案可以让飞机提前获取前方阵风信息,根据主扰动量对飞机的载荷影响,提前生成控制指令,减少由于控制回路延迟与传感器对数据测量延迟所带来的影响,以及由于速率限制所导致的速率饱和影响,从而加强控制器对阵风减缓的控制能力。
4 阵风减缓效率对比分析
为了量化基于风扰动预测的阵风减缓的效果,定义增加控制律时的减缓效率如下:
(12)
式中,σ为未加控制律时开环系统输出的均方根值,σ′为增加控制律时闭环系统输出的均方根值。
图11为连续突风下的对翼尖加速度的控制效率对比图,从图中明显可以看出,其前馈控制的效率值在控制器自适应的前期阶段,在某一范围内不断振荡并逐步递增,最后逐渐平稳收敛于一固定的效率值。说明相比于传统反馈PID控制,前馈控制方案能具备更高的减缓效率。

图11 连续突风下的对翼尖加速度的控制效率
在不考虑系统非线性因素的情况下,传统PID反馈控制与自适应前馈控制的阵风减缓对比效率,如表1所示。从表中可以看出,后者的阵风减缓效果,明显优于前者。在翼尖加速度与质心加速度的减缓指标上有着较为明显的减缓效果,而对翼根弯矩以及翼根扭矩的载荷指标也有一定的控制作用。
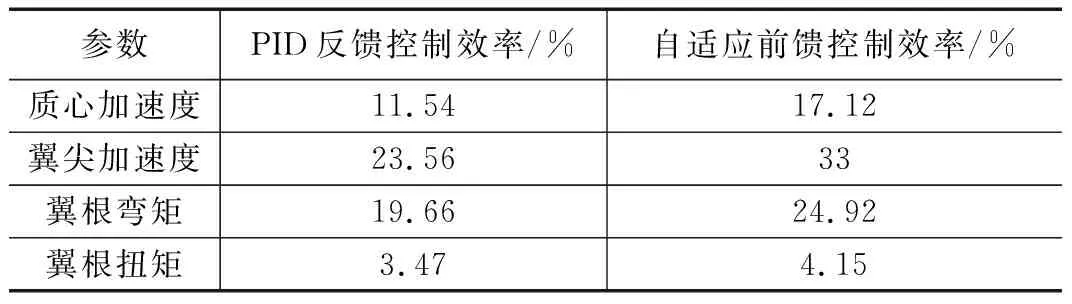
表1 阵风载荷减缓效率对比
进而针对舵偏行程饱和、速率限制和延迟这3种系统非线性因素,分别对比其在PID反馈控制与自适应前馈控制下的各项系统指标,结果如表2所示。从表中可以看出,在考虑单一系统非线性因素时,结合新的阵风探测方式的前馈控制较为明显地降低了阵风减缓对系统指标的要求。其中,在阵风减缓效率统一达到18%的情况下,相比于传统PID控制,自适应前馈控制对控制舵面的限制指标明显放宽,其最大舵面偏转速率与角度的限制要求都有所降低。并且对系统延迟指标影响也较为明显,其系统所允许的延迟时间限制要求从30 ms提升到50 ms。充分地说明在实际工程中,后者相比于前者,对系统具备更好的兼容性,能有效提高系统的最低延迟限制,并降低作动器的工程限制要求。
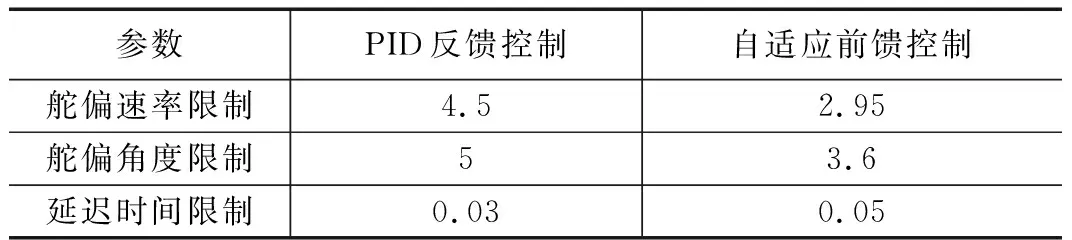
表2 系统影响指标对比(在阵风减缓效率18%情况下)
5 结束语
本文充分考虑了实际工程状况中控制面偏转角度、偏转速率受限约束以及系统延迟的影响,建立了包含非线性因素的系统模型,并在阵风减缓反馈控制基础上引入了基于风扰动预测的自适应前馈算法。其主要思想是利用能探测风扰动信息的机载设备,使得在飞机到达风场前提前获取阵风信息,并根据预测到的风场信息设计前馈补偿算法;再利用飞机模型反馈的载荷信息进行自适应控制,进而增强阵风减缓控制的执行效果。
研究结果表明,上述的系统非线性因素对飞机阵风载荷减缓影响显著,其减缓效果与控制面的偏转限制紧密关联,而延迟对系统稳定性更是存在重大影响。而本文建立的前馈控制方案与传统PID反馈控制相比,能在预测模型中包含前视阵风信息,且结合考虑了控制面偏转的约束,能有效抑制阵风载荷。对于民机阵风载荷减缓系统的设计与验证而言,更具有实际工程意义,特别是针对系统非线性因素的考虑,使其对系统控制方案的研究具备更多的参考价值。

