基于遥测技术的新型传感器柔性结构振动优化控制方法

高翔霄， 任月慧， 李思翀， 王宇红， 翟 晋

(北京宇航系统工程研究所，北京 100076)

0 引言

随着新型传感器不断应用在各种传感探测领域，对新型传感器装置的柔性结构的振动稳定性提出了更高的要求，相关的新型传感器柔性结构控制方法研究受到人们的极大关注[1]。

当前，大多采用人工智能技术和控制技术进行新型传感器柔性结构的振动稳定性控制，结合对新型传感器柔性结构的姿态参数调节，提高振动控制的效能。传统方法中，对新型传感器柔性结构的振动的姿态参数调节分为确定性成分和不确定性成分两部分，结合对振动结构参数调节和振动动力学分析方法[2-3]，进行新型传感器柔性结构振动的控制律设计，文献[4]中提出基于二次型调节模型的新型传感器柔性结构振动控制方法，采用模糊控制方法进行参量自适应调节，提高新型传感器柔性结构控制的稳定性，但该方法的抗干扰性不好，控制输出为稳态性不强。文献[5]中提出基于双闭环LQR控制的新型传感器柔性结构振动抗扰控制方法，解决新型传感器柔性结构输出迟滞的问题，但该方法进行传感器控制的自适应性不好。

针对上述抗干扰性和自适应性不好的问题，本文提出基于遥测技术的新型传感器柔性结构振动优化控制方法。构建新型传感器柔性结构振动动力学模型，采用气弹模态参数识别方法，利用遥测技术进行新型传感器柔性结构振动惯性参数识别，实现新型传感器柔性结构振动优化控制。最后进行仿真实验分析，展示了本文方法在提高新型传感器柔性结构振动优化控制能力方面的优越性能。

1 新型传感器柔性结构振动动力学模型及参数识别

1.1 新型传感器柔性结构振动动力学模型

为了实现新型传感器柔性结构振动优化控制，首先构建新型传感器柔性结构的振动动力学参数模型。

遥测技术是包括输入设备、输出设备、传感器和变换器4种单元的遥测系统，其可以通过变换器把电信号转换成适合不同路径传输与不同设备要求的信号，从始端到终端都要保证信号不失真。采用融合传感跟踪识别技术，进行新型传感器柔性结构控制的姿态参数采集，构建新型传感器柔性结构的参数自适应融合模型，结合Kalman滤波融合方法，进行遥测柔性动力学参数调节和振动反馈调节[6]，采用陀螺仪、加速度计以及磁力计等敏感元件，进行新型传感器柔性结构的振动性控制，由于在进行柔性操作的时候，其负载率具有强耦合、非线性、多输入输出的特性，因此需要进行建模分析。新型传感器柔性结构的振动控制模型的总体设计构造如图1所示。

图1 新型传感器柔性结构振动控制的总体结构模型

根据图1所示的新型传感器柔性结构振动控制的总体设计结构图，在速度坐标系、体坐标系的坐标系下，进行新型传感器柔性结构振动特征量的遥测设计，构建新型传感器柔性结构的振动动力学和运动学模型[7]，因为传感器内部的覆盖面积是有限的，且存在大量的接触面信息，因此在精确测量的过程中需要测量的面积较大。依据这个条件，对多个离散的传感器进行有序组合，才形成传感器的阵列结构，使得每个单元都很有规则的排列在传感器组合中，以此达到对传感器内部的三维控制，提高传感器的检测效果。其中，最重要的是传感器的单元结构设计。首先对传感器信号进行数字化和预处理，然后传输到主机当中，进行数据处理和数据分析。

在系统运行过程中，传感器的电信号随之变化，因此传感器的电信号输出大部分仍是模拟信号，而将信号进行数字化是保证信号稳定传输的主要方式之一。应用数字传感信号处理器，将信号的偏移和增益利用数字技术进行控制，在数字域中，保证传感器信号的校准和补偿。

传感信号预处理的过程是首先将传感器数字信号进行输出量和标注量的标记，利用某种或标准器具对传感器进行定点标度，称之为标定，以此确定系统传感器所受的压力，校准信号电信号与压力之间的函数关系。

在遥测技术下，构建新型传感器柔性结构的振动动力学方程描述如下。

纵向振动：

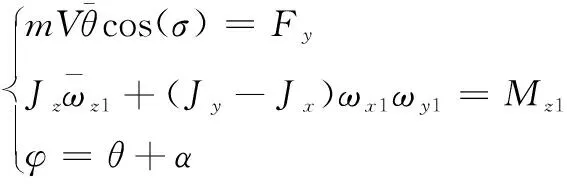
(1)

侧向振动：

(2)

横向振动：

(3)

其中:m为新型传感器柔性结构的质量，V为速度矢量(Ox2轴)与水平面间的转矩，Fy为新型传感器柔性结构振动惯性矩，Jz为柔性结构的振动扰动矩，Mz1为传感器柔性结构系统惯导气动力转矩，θ为振动力学的相位角，α为侧向推动力，采用气弹模态参数识别方法，构建新型传感器柔性结构的振动运动学模型描述为如下非线性方程组：

(4)

其中:P为新型传感器装置的俯仰力矩，SM为法向加速度，lR为新型传感器柔性结构对体坐标系Oz1的惯性积，q为纵向运动力矩。综上分析，构建了新型传感器柔性结构振动动力学模型。

1.2 柔性结构的振动力学参数识别

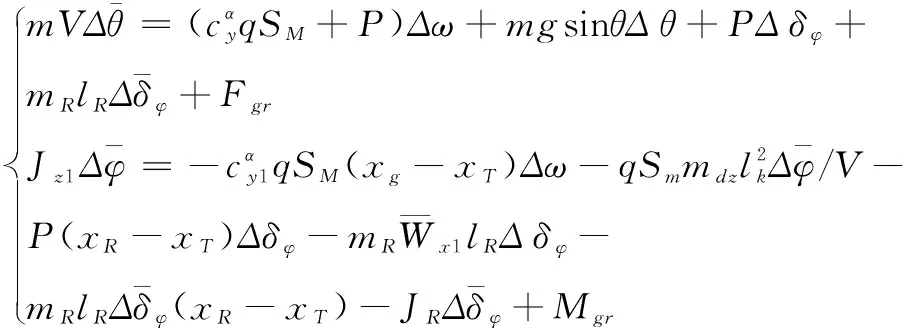
(5)

其中:ω为新型传感器柔性结构的转动相位角，Fgr表示旋转矩，JR表示新型传感器柔性传动惯量，Mgr表示惯性中心分布特征量，采用四阶龙格库塔法进行遥测设计，在柔性动力学参数模型，进行新型传感器柔性传动的在线估计。

在对新型传感器信号进行记录、显示和处理的过程中，为精准获得传感器信号，求解新型传感器柔性结构的状态量约束方程，选择最优控制律下，采用模态识别方法，进行柔性结构的振动力学参数识别，得到参数的优化模型为：

(6)

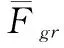
由此实现了柔性结构的振动力学参数识别，采用模糊反馈调节方法进行新型传感器柔性结构的振动误差修正和纠偏控制，实现新型传感器柔性结构自适应鲁棒控制。

2 新型传感器柔性结构振动优化控制

2.1 振动模态参数的遥测优化

在上述构建新型传感器柔性结构振动动力学模型的基础上，进行柔性结构的振动优化控制设计。传感器的受力点是在各单元的各个节点相对独立情况下实现的，即假定传感器受外力时，受力点的形变可忽略，因此采用卡尔曼滤波方法实现对新型传感器柔性结构振动参数的融合调节和小扰动抑制，采用卡尔曼滤波方法实现对新型传感器柔性结构振动参数的融合调节和小扰动抑制处理，容积卡尔曼滤波函数表示为：

(7)

式中，φa、ψa、γ为新型传感器柔性结构在横向、侧向和纵向方向上的自适应控制参数，b1、b2、b3、d3为遥测控制变量，为已知系数，Δb1、Δb2、Δb3、Δd3为新型传感器柔性结构的外力矩，fd1、fd2、fd3为扰动力矩，δφ、δψ、δγ为新型传感器柔性结构末端估计参数值。

假设新型传感器柔性结构的遥测状态特征量关于x1Oy1平面对称，采用Lyapunov求导方法[9]，得到新型传感器柔性结构的遥测状态参数调节模型为：

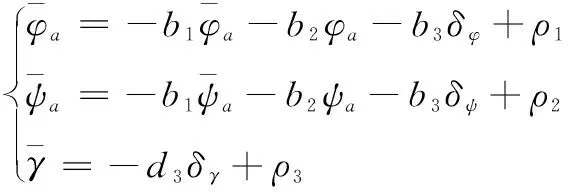
(8)

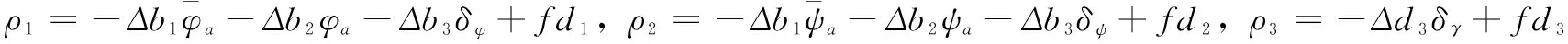
由于新型传感器柔性结构的阻尼力、位置力是线性变化的，在线性振动下，基于遥测技术，得到柔性结构的稳定性特征量描述为：

(9)

式中，b>0，φa为正向运动学参数估计的差值，u为新型传感器柔性结构振动的遥测参数，fd为遥测惯性特征序列，结合反演微分控制方法，实现新型传感器柔性结构的遥测优化。

2.2 控制律的优化设计

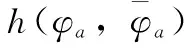
M=Mn+ΔM

(10)

(11)

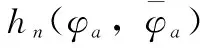
在卡尔曼滤波预估模型中实现对动力学模型的线性化处理，在扩展卡尔曼滤波模型下，新型传感器柔性结构振动轨迹预测方程表示为：

(12)

其中：

(13)

(14)

在初始化的遥测参数中，采用自适应滑模控制方法，得到新型传感器柔性结构的振动参数调节模型为：

ISM1+IL1+INa1+IK1+IT1+Isyn1]

(15)

其中:VTh表示振动阈值，τh表示振动时延，τw表示新型传感器柔性振动控制时间窗口，如果f(x1,x2)已知，得到新型传感器柔性结构振动控制输出的唯一解为：

u*=-kceV-f(x1,x2)

(16)

误差反馈输出：

(17)

若设eV=0，新型传感器柔性结构的振动载荷pi(t)(i=1,2,3)，控制增益的表达式如下：

(18)

综上分析，得到新型传感器柔性结构的振动力学参数预测值：

J=

(19)

根据Lyapunov稳定性原理，结合状态反馈调节方法进行稳定性控制，至此，实现新型传感器柔性结构振动优化控制[10]。

3 仿真实验与结果分析

为了验证本文方法在实现新型传感器柔性结构振动控制中的应用性能，基于STALLVib和Matlab仿真软件进行新型传感器的柔性机构振动力学参数采集，采用工业机器人进行柔性结构的振动标记，实验模型如图2所示。

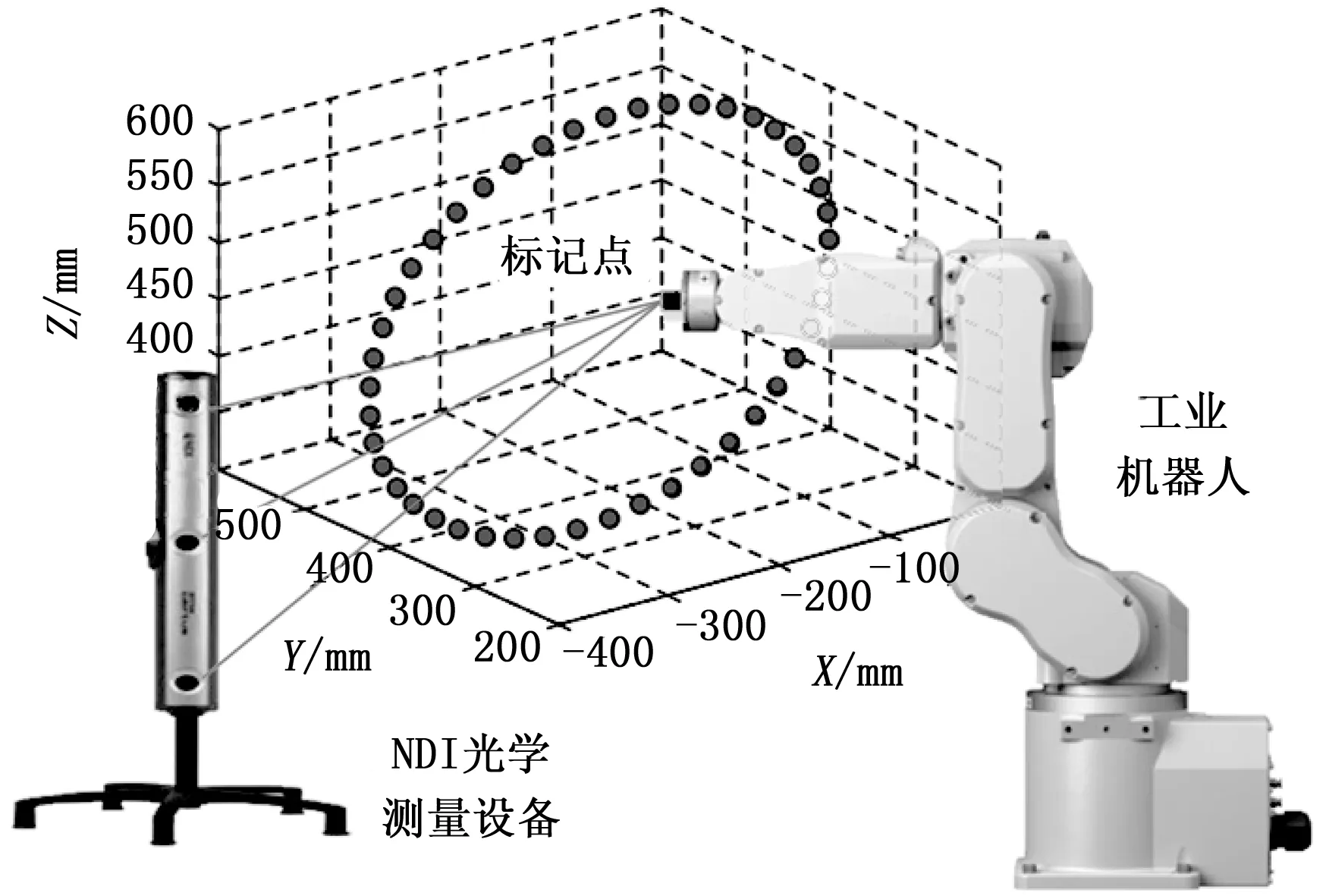
图2 实验仿真模型

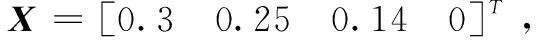
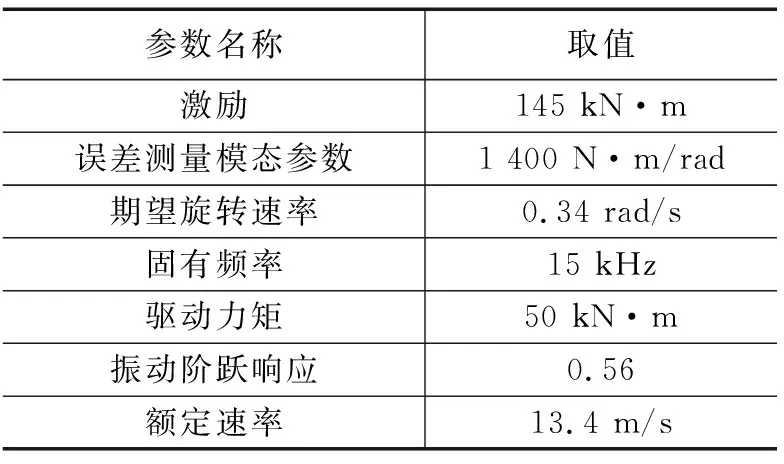
表1 仿真参数设定

根据上述仿真环境和参数设定，进行新型传感器柔性结构振动控制仿真分析，得到振动数据分布结果如图3所示。

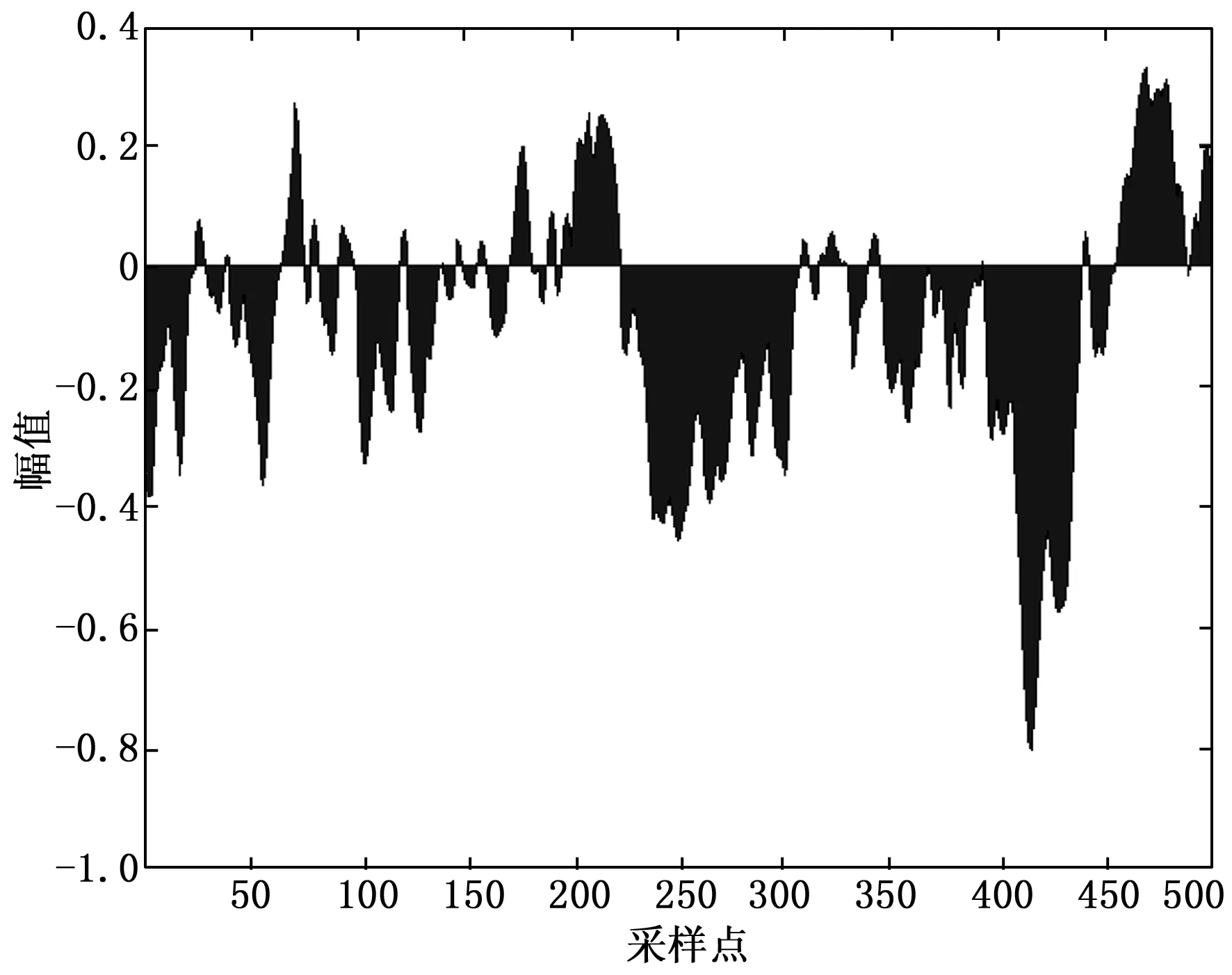
图3 振动数据分布

图3采集的新型传感器柔性结构振动数据为输入，进行新型传感器柔性结构振动控制，提取新型传感器柔性结构振动特征量，采用遥测技术进行新型传感器柔性结构振动惯性参数识别，在存在扰动误差和建模误差的条件下，得到控制输出如图4所示。

图4 新型传感器柔性结构振动控制输出

分析图4得知，本文的建模能够对新型传感器柔性结构振动进行控制，控制误差较小，且无限拟合，说明采用本文方法进行新型传感器柔性结构振动控制的输出稳定性较好。

将本文方法与文献[3]、文献[4]方法进行对比，测试输出误差，在不同的迭代次数下通过最小均方根误差的数值大小得到对比结果见表2，

表2 最小均方根误差

分析表2得知，本文方法进行新型传感器柔性结构振动控制的输出最小均方根误差较小。本文方法的在迭代次数为100时的误差最大为0.034，在400时的误差最小为0.002，皆高于文献[3]和文献[4]的误差值，由此可得出实际应用性能较强的结论。

4 结束语

本文提出基于遥测技术的新型传感器柔性结构振动优化控制方法。构建新型传感器柔性结构振动动力学模型，选择最优控制律下，采用模态识别方法，采用遥测技术进行新型传感器柔性结构振动惯性参数识别，结合状态反馈调节方法进行稳定性控制，实现新型传感器柔性结构振动优化控制。实验分析得知，本文方法进行新型传感器柔性结构振动控制的输出稳定性较好，误差较低。但数据的实际应用仍需进行实例验证，且在未来的研究中，将致力于实际应用性能，再具体的真实环境下，验证并进一步改进所设计控制方法的性能。