基于BP神经网络的富水砂层渣土改良试验效果预测
展 超
(中铁一局集团城市轨道交通工程有限公司,江苏 无锡 214000)
0 引言
随着国家基础设施建设的高速发展,地铁成为城市交通建设不可或缺的部分。南昌地区富水砂层具有内摩擦角大、渗透系数高等特点,容易造成喷涌、结泥饼等事故,会直接减缓盾构的掘进速度,降低掌子面的稳定性[1-2]。为避免工程事故的发生,对盾构区间所处地层进行渣土改良效果预测显得尤为重要。
渣土改良效果主要以渣土的和易性、渗透性和流动性作为评价指标[3],国内外学者针对渣土改良试验对其坍落度、渗透系数和内摩擦角等物理性能参数进行了研究。Andrea等[4]为了减小刀盘刀具在砂卵石地层掘进时的摩阻力,通过渣土改良试验以增强砂卵石在盾构压力室中的流动性,从而降低螺旋输送机卡顿的风险;QU Tongming等[5]基于PFC 3D和FLAC 3D 2种有限元分析软件对土压平衡盾构在砂土地层的渣土改良进行了模拟,得出改良后的渣土颗粒流动性更强,并能减小掌子面的土压力,从而降低刀盘的转矩和推力;WANG Shimin等[6]在福州高水压高渗透率地层采用泥水-膨润土-CMC有机化合物进行渣土改良系列试验,提出适用于该地区的改良剂掺入比;肖超等[7-8]以南昌地铁1号线为工程依托,通过膨润土和高分子聚合物对砾砂、泥质粉砂岩进行改良,同时开展室内土工试验测试其强度参数,得出渣土力学性质参数的变化规律;莫振泽等[9]以无锡富水粉砂层盾构区间为工程背景,提出适用于该地区的浓泥改良技术,在改良试验中能提高坍落度数值,增强渣土的流动性、和易性,同时还可以在掌子面形成泥膜,有效降低盾构在富水粉砂地层掘进过程中的孔隙水压力;叶晨立[10]以福州地铁高水压高渗透性的砂土地层为研究背景,使用膨润土、CMC高分子聚合物对其开展改良试验,通过对比试验得出该地层的有效改良方案;叶新宇等[11]以南昌地铁某区间为工程背景,以泥质粉砂岩为研究对象,通过改良试验得出渣土的最佳坍落度为17~20 cm,并通过理论推导得到改良剂性能参数与坍落度的函数关系式;刘彤等[12]结合室内发泡和现场改良试验结果,得出泡沫剂和膨润土的最优质量分数,并提出适用于南昌地区富水砂层的最佳改良方案;江长通等[13]基于BP神经网络模型并结合室内土工试验数据对黄土的力学参数进行预测,测试结果的整体误差均在允许范围内。
目前,现有研究多数采用室内土工试验对渣土改良效果进行评价和分析,人工神经网络在地铁建设中的应用以预测地表沉降为主,而通过BP神经网络结构对渣土改良效果的预测却鲜有报道。本文以南昌地铁4号线盾构区间为研究背景,基于BP神经网络建立适用于富水砂层地区渣土改良试验的效果预测模型,选取改良试验的主要影响因素和性能评价指标,经过模型的映射训练后,对改良后的坍落度、渗透系数和内摩擦角进行精准预测,并分别把实际值与预测值进行对比分析,以期为今后富水砂层地区的类似地铁工程提供理论参考。
1 BP神经网络模型
1.1 基本原理
BP神经网络模型通过模拟生物神经元的连接结构,对其进行信号的输入和输出,以达到模拟大脑学习、推理和归纳等功能。BP神经网络以其非线性映射、自学习、自适应、容错能力等性能优势被广泛地应用于各个领域[14]。
BP神经网络是一种基于误差反向传播训练的多层前馈网络,主要分为输入层、隐含层和输出层,各层神经元相互全连接,同层神经元无连接[15]。BP神经元网络模型通过Sigmoid和Relu等常用传递函数实现输入层和输出层的任意非线性映射关系,网络结构如图1所示。
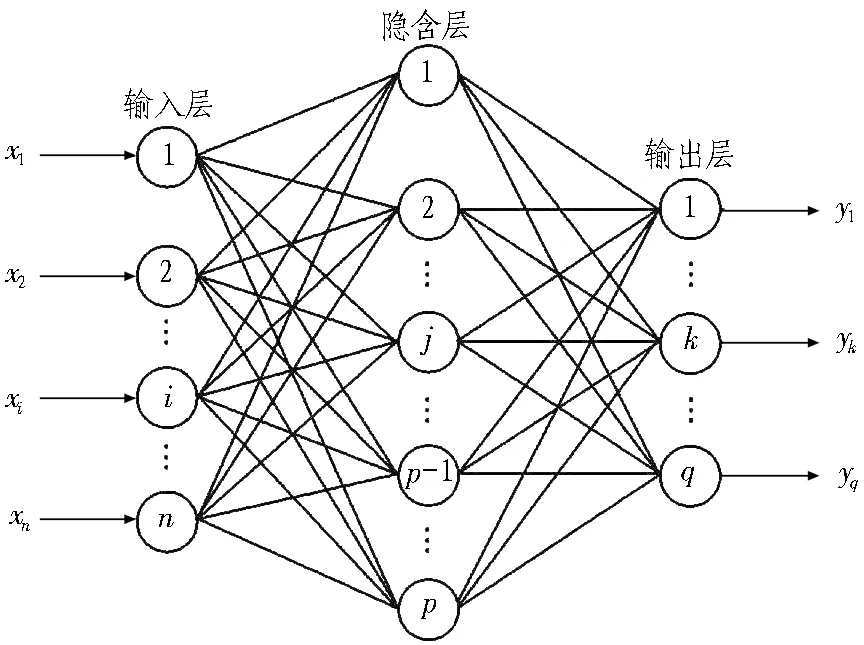
图1 网络结构示意图Fig.1 Diagram of network structure
在BP神经网络模型的训练过程中,主要由信号的正向传播和误差的反向传播2部分组成。主要表现为上一神经元的信号由输入层传入,经隐含层传向输出层,若能够得到期望的输出值,则训练过程结束;若未能得到理想的输出结果,则利用梯度下降法修正误差信号的连接权值,使得误差信号最小,最终得到理想的输出值。计算流程如图2所示。
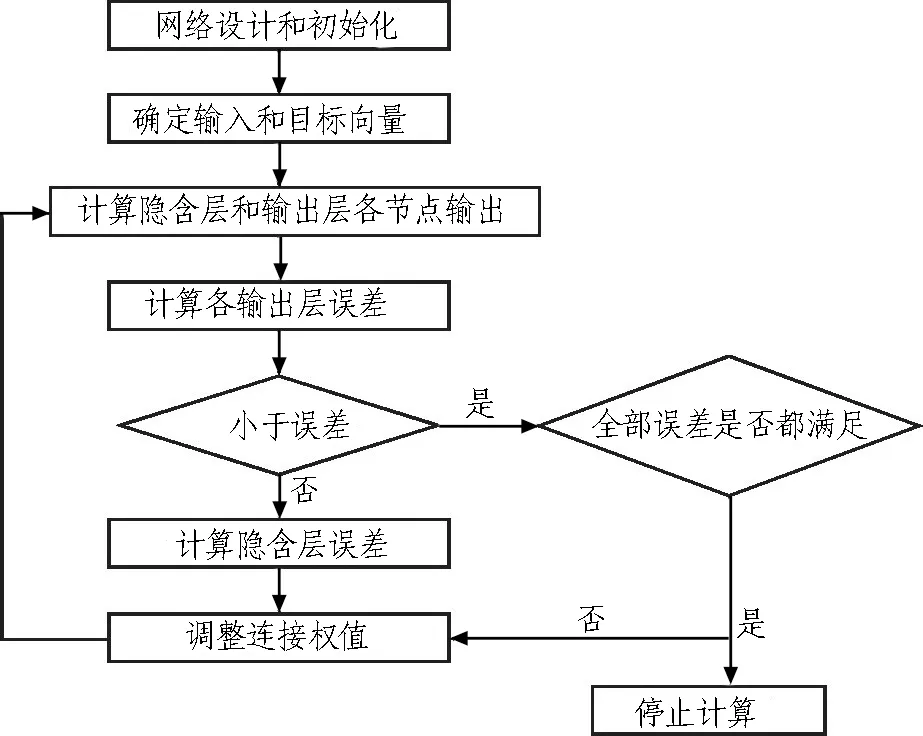
图2 BP神经网络计算流程图Fig.2 Calculation flowchart of BP neural network
1.2 信号正向传播算法
当信号正向传播时,数据信号从输入层传入,经隐含层传向输出层,若输出的实际值与理想值差异较大,则误差反向传播进行修正。以某一BP神经网络结构为例,输入层节点数为m,隐含层节点数为n,输出层节点数为p,则有以下关系。
第i个神经元结构的输入为
(1)
式中:wik为输入层第i个神经节点和输出层第k个神经节点间的连接权重;ok为输出层第k个神经节点的输出值。
第i个神经元结构的输出为
oi=fSigmoid(hi)。
(2)
式中fSigmoid为节点i和k之间进行传递激活的Sigmoid函数。
1.3 误差反向传播算法
在信号正向计算过程中,如果输出的实际值与理想值不一致,就需要将误差信号经隐含层反向传播至输入层,此时选取误差目标函数为
(3)
式中:yik和oik分别为输出的理想值和实际值;m为输入层节点数。
各样本的误差加权值
(4)
修正误差权值
(5)
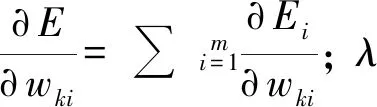
在误差反向传播时,利用式(4)和式(5)不断修正加权系数,将误差传递给各层的神经元结构,实现神经元之间连接权重的实时调整,直至输出层得到理想的输出结果为止。
2 选取影响因素和评价指标
2.1 工程概况
南昌市轨道交通4号线丁家洲站—观洲站盾构区间(SK16+953.892~SK18+059.225)出丁家洲站后沿抚生南路向北方前行,在云飞路北侧下穿桃花河南支渠引水箱涵后继续向北进入观洲站。盾构区间沿线主要掘进地层为富水砂层,颗粒级配试验结果如图3所示。
由图3筛分数据可知,2 mm以上颗粒组的占比高达46.46%,粒径在0.25 mm以下的颗粒仅占4%左右。在盾构掘进过程中,刀盘会扰动砂层的原始状态,使其变得松散进而可能会造成喷涌等事故。为提高渣土改良预测模型的精度,降低施工险情的发生频次,确定安全事故的关键影响因素显得尤为重要。
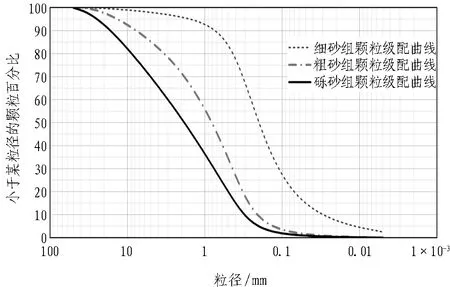
图3 颗粒级配曲线Fig.3 Curves of grain gradation
2.2 主要影响因素
渣土改良试验中存在各种影响因素,这些因素将直接减缓盾构在富水砂层中的掘进速度,而基于BP神经网络构建预测模型则必须考虑这些关键因素。从力学性质和外掺改良剂的角度,将影响渣土改良试验效果的因素归纳为以下2方面。
2.2.1 渣土的物理力学参数
南昌地区富水砂层具有强透水性,地层的渗透系数达到10-2cm/s数量级,渣土的排水固结容易使工作面发生喷涌的险情,从而导致工作面的水土压力不平衡,盾构难以加快推进速度。内摩擦角造成盾构刀盘及螺旋输送机的摩阻力过大,经改良后可以减小刀盘转矩和盾构推力,减缓刀盘刀具的磨损情况,降低因换刀而引发的安全事故发生率。电阻率是富水砂层的固有力学特性之一,也是区分砂类和其他种类土体的重要参数,将三者结合可反映出南昌地区富水砂层的基本物理力学性质和结构特性。因此,本文选取渣土的渗透系数、内摩擦角和电阻率来反映其物理力学性质,并将这3个指标作为预测模型的输入变量。
2.2.2 渣土改良外掺剂质量分数
在施工中常以膨润土、泡沫剂作为改良外掺剂。泡沫剂中含有可溶于水的亲水基和不溶于水的憎水基,是典型的双亲分子结构,在压缩空气的高压冲击下,将双亲分子结构表面的气泡打破,形成改良所需的泡沫。由于砂粒具有较大的孔隙比,颗粒结构较为分散,气泡未能充分溶于颗粒间,膨润土遇水膨胀并呈黏稠糊状液体,静电吸引力使晶胞间距增大,与渣土颗粒混合后可有效填充于砂粒空隙中,并形成一层膨润土泥膜,增强渣土的黏聚性。改良作用原理如图4所示。
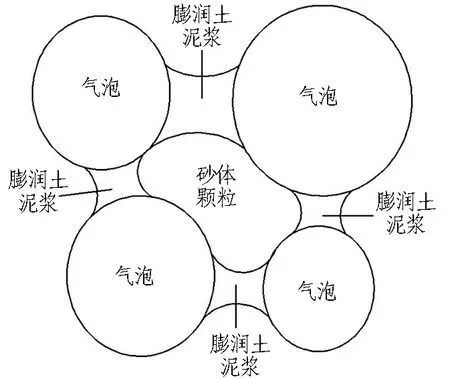
图4 改良作用原理示意图Fig.4 Diagram of ground conditioning effect
当改良剂质量分数较低时,不会使土体的渗透系数和内摩擦角显著降低;当质量分数较高时,则不能充分发挥外掺剂的改良性能,同时还会增大成本投入。经综合考虑经济性和配合比试验结果,最终选取泡沫剂质量分数为1%、2%、3%、4%、5%,膨润土泥浆质量分数为7%、9%、11%、13%,并将改良外掺剂的质量分数作为模型的输入变量。
本研究所用泡沫剂均为西安某新材料科技有限公司生产的盾构专用泡沫剂,并按照泡沫原液与水的质量比为1%、2%、3%、4%、5%配制所需质量分数的泡沫剂溶液。相关研究表明,泡沫半衰期大于5 min,发泡倍率在10~20倍均可以满足盾构施工要求[16]。现场对这5种质量分数的泡沫剂溶液进行测试,得到不同质量分数泡沫剂溶液的半衰期和发泡倍率,具体测试结果如表1所示。
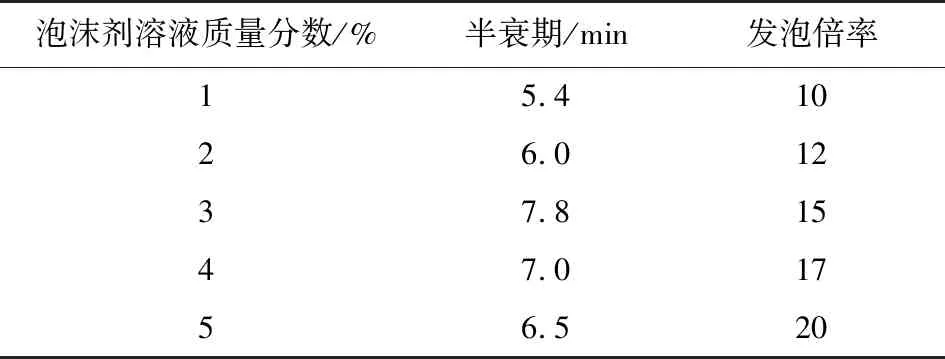
表1 不同质量分数泡沫剂溶液的半衰期与发泡倍率Table 1 Half-life and foaming ratio of foaming agent solutions with different concentrations
2.3 评价指标
目前,国内外主要以渣土改良后的和易性、渗透性和流动性作为评价标准[17]。本文将以下3个性能指标作为输出变量。
2.3.1 坍落度
通过测试坍落度数值,可以有效反映渣土改良后的和易性,这将直接影响土舱内的渣土流动状况,同时也决定了渣土外排的难易程度,一般以160~200 mm为标准。
2.3.2 渗透系数
经现场实践表明,渣土的渗透系数越小,则越有利于盾构顺利掘进。当渗透系数小于10-5cm/s时,渣土可以在螺旋输送机口形成“瓶塞效应”,有效预防喷涌事故。
2.3.3 内摩擦角
通过检测渣土改良后内摩擦角的变化,可以得出改良剂在试验过程中的作用效果,内摩擦角减小8~10°,则表明改良剂充分作用于颗粒之间,能够增强渣土的流动性。
3 渣土改良试验的预测模型
3.1 选取样本数据
在坍落度试验前,对渣土试样进行渗透试验、直剪试验和电阻率测试,随后将静置24 h的膨润土泥浆溶液、充分发泡的泡沫液与渣土均匀搅拌后进行坍落度试验,并再次测得渗透系数和内摩擦角,最终得到数据样本集。数据样本集如表2所示。其中,前24组为训练集,中间8组为验证集,后8组为预测集。
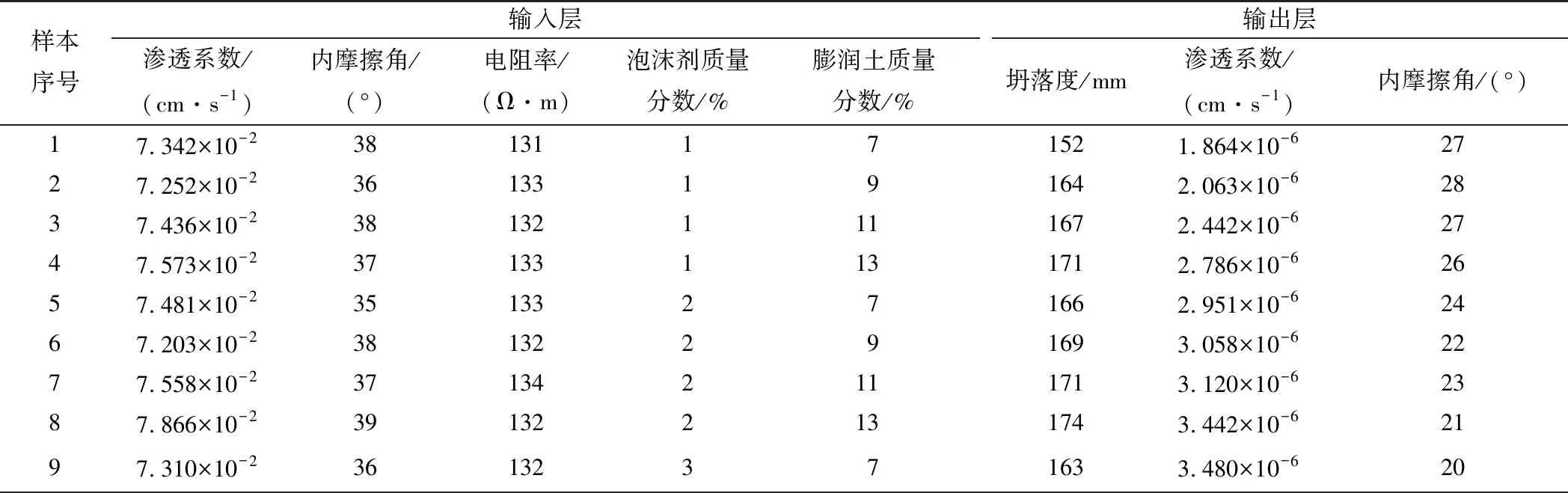
表2 数据样本集Table 2 Data sample set
表3示出了样本数据的统计参数。输入变量中的渗透系数呈负偏态分布,内摩擦角和电阻率呈正偏态分布,而改良外掺剂质量分数呈现出正态分布;在输出变量中,坍落度和渗透系数呈低程度的负偏态分布,内摩擦角呈正偏态分布。所有样本数据的离散系数都极低,表明数据的离散程度小。统计结果表明,样本数据呈“低峰瘦尾”分布,即数据的分布峰度低于正态分布,且尾部数据的分散程度较低,反映出数据的分布情况较为均匀,表明样本数据具有良好的代表性。
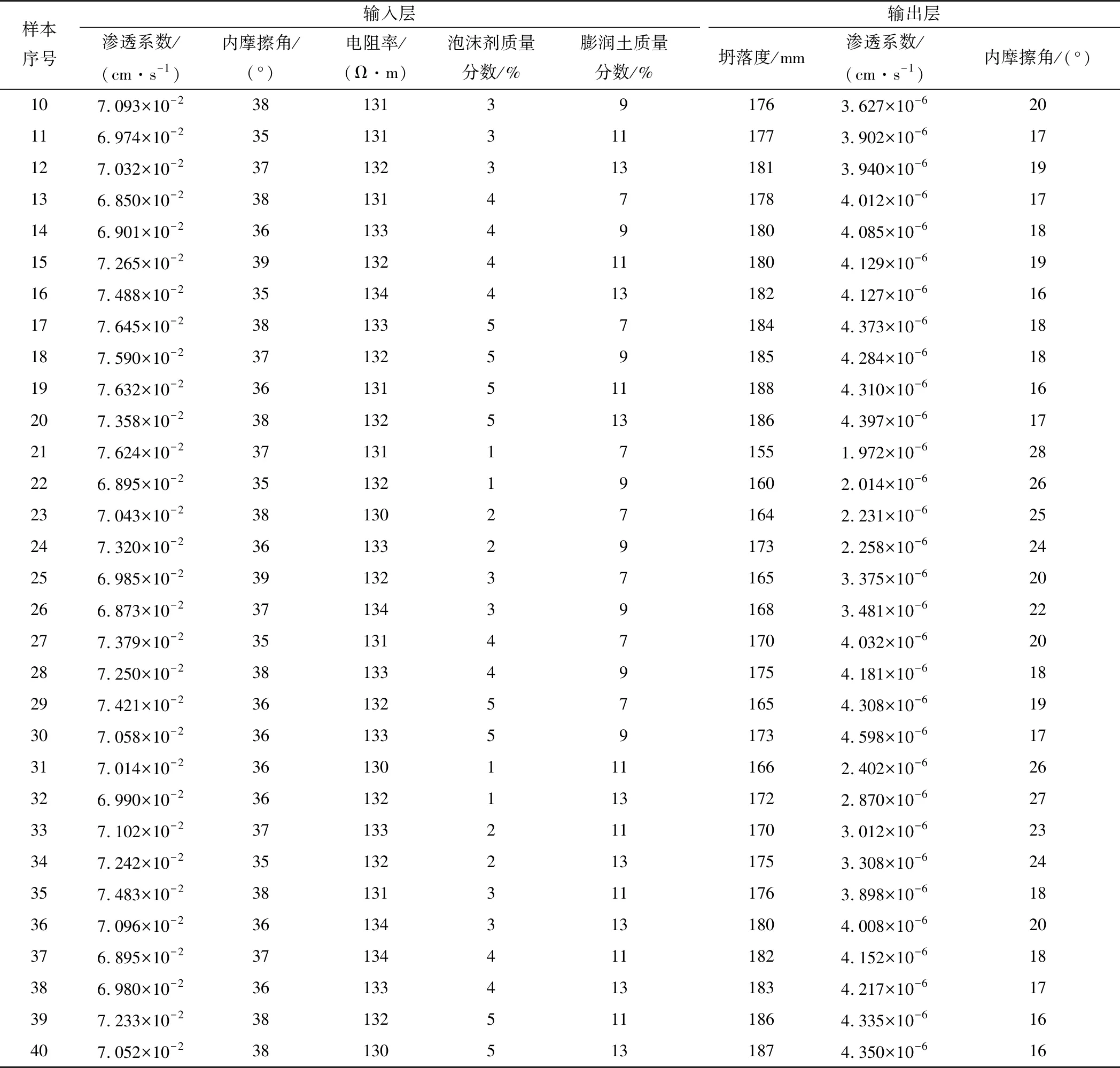
表2(续)

表3 样本数据的描述性统计Table 3 Descriptive statistics of sample data
3.2 数据归一化处理
表2中数据的量纲差异性较大,为了能够使预测结果更加精准,将输入、输出数据统一转化为[0,1]区间内的量纲值,以减小不同数据间的量纲差异,提升训练效率和精度。通常采用下式进行归一化处理:
(6)

由于篇幅有限,不再展现归一化处理后的数据。
3.3 建立BP神经网络模型
为加快模型的计算收敛速度,本文采用具有1个隐含层的3层神经网络模型。输入层有5个节点,分别是渗透系数、内摩擦角、电阻率、泡沫剂质量分数和膨润土质量分数;输出层有3个节点,分别是坍落度、渗透系数和内摩擦角;而隐含层的节点数将直接影响神经网络预测模型的精度,过多和过少的节点数都会导致预测过度或误差较大的问题。所以,按照下式进行确定:
(7)
式中:l为隐含层的节点数;m和p分别为输入层、输出层的节点数;a为1到10之间的调整常数。
通过式(7)试算隐含层的节点数为3时,模型既能满足误差的要求,又能保证结构的紧凑性,还能使得计算误差最低。因此,建立结构为5-3-3的BP神经网络模型,如图5所示。
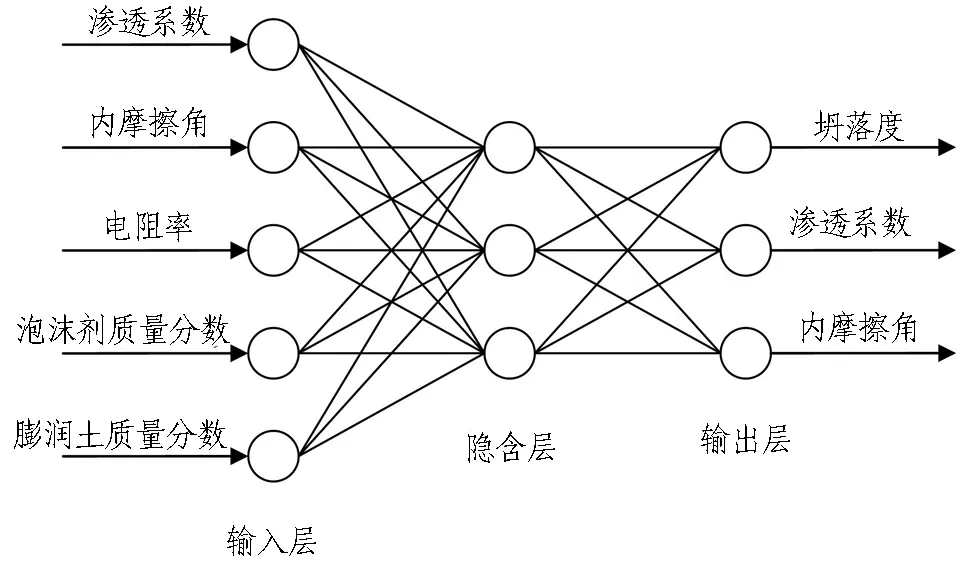
图5 BP神经网络模型结构Fig.5 Structure diagram of BP neural network model
3.4 网络结构的训练
为提高训练效率,加快收敛速度,采用SPSS 25.0的神经网络工具箱进行训练和预测。在训练过程中,模型选用Traingdm为训练函数,Sigmoid为激活函数,目标误差设定为0.001,学习速率为0.01,动量常数为0.9,学习过程中的误差变化曲线如图6所示。由图6可以看出,当训练次数接近6 000次时,神经网络模型基本达到目标误差的范围以内,即该模型符合预测精度要求。
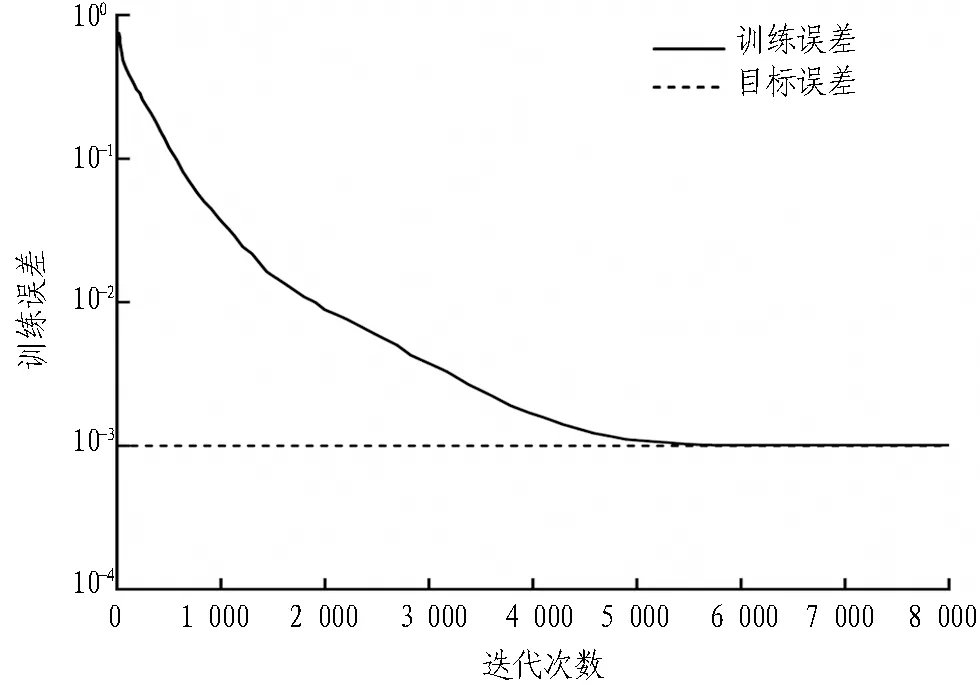
图6 模型训练误差的变化曲线Fig.6 Variation curve of model training error
4 预测结果分析及其检验
4.1 预测结果分析
本文所建立的BP神经网络模型经过训练和验证后,可以得到训练集和验证集的预测值,按下式将其与实际值进行相对误差评价。
(8)
图7—9分别为3种输出指标预测值与实际值的对比关系图。由图7—9中可以看出,坍落度和渗透系数的曲线在小范围内上升,而内摩擦角的曲线是小幅度下降,这是由于改良剂质量分数的逐步增大,使改良后的渣土流动性和渗透性随之增强,内摩擦角则在润滑作用下显著降低。
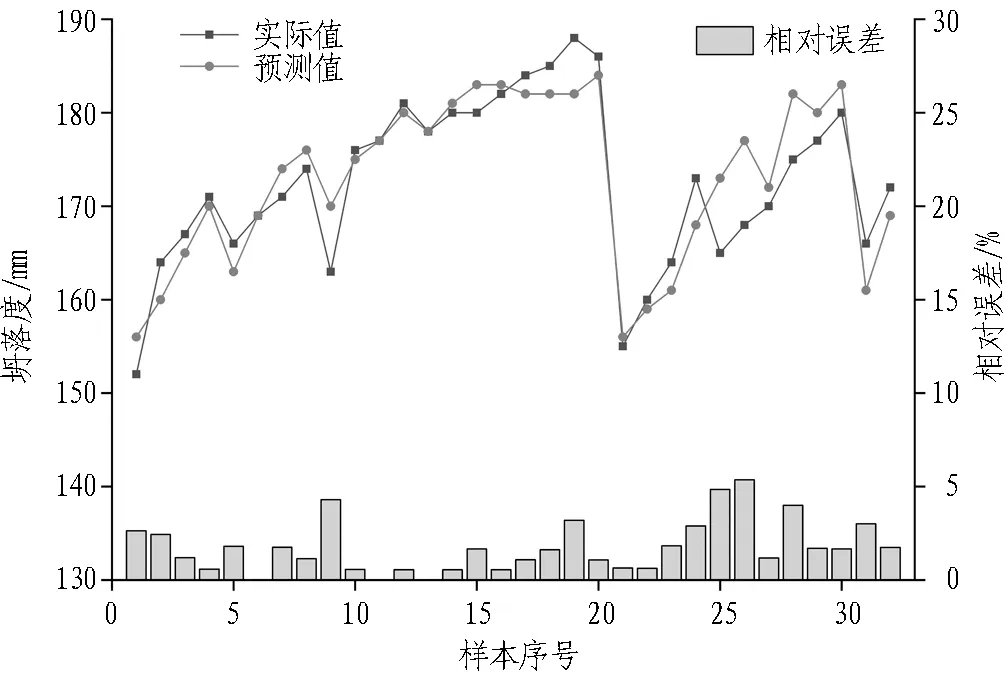
图7 坍落度的对比关系图Fig.7 Comparison of slump
由图7可知:坍落度实测值的变化区间为150~190 mm,而预测值均在此区间内,并且平均预测值为172.8 mm;曲线出现了陡降关系点,这是由于第20个样本和第30个样本的泡沫剂质量分数从5%降到了1%,而膨润土质量分数分别从13%降至7%、9%升至11%,该质量分数与第1个样本和第3个样本的配比一致,导致坍落度数值也降至同一水平。
由图8可知:渗透系数在改良作用中从10-2cm/s大幅度降低至10-6cm/s数量级,平均预测值达到了3.355×10-6cm/s;曲线的变化趋势与图7相似,前期呈斜率逐渐减小的上升趋势,渗透系数由于改良外掺剂质量分数变化产生陡降现象后从初始水平继续上升,直至曲线出现第2次陡降。
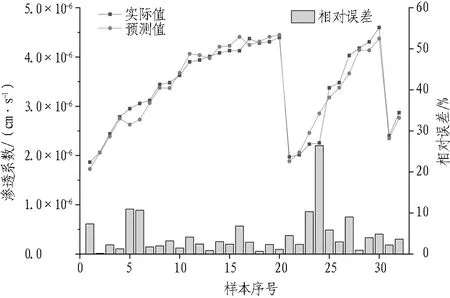
图8 渗透系数的对比关系图Fig.8 Comparison of permeability coefficient
由图9可知:内摩擦角的变化趋势是先逐渐减小,随后在改良剂质量分数发生显著变化的陡降点处上升至改良的初始水平,接着又逐步降低,整个预测趋势的平均值为21.6°。
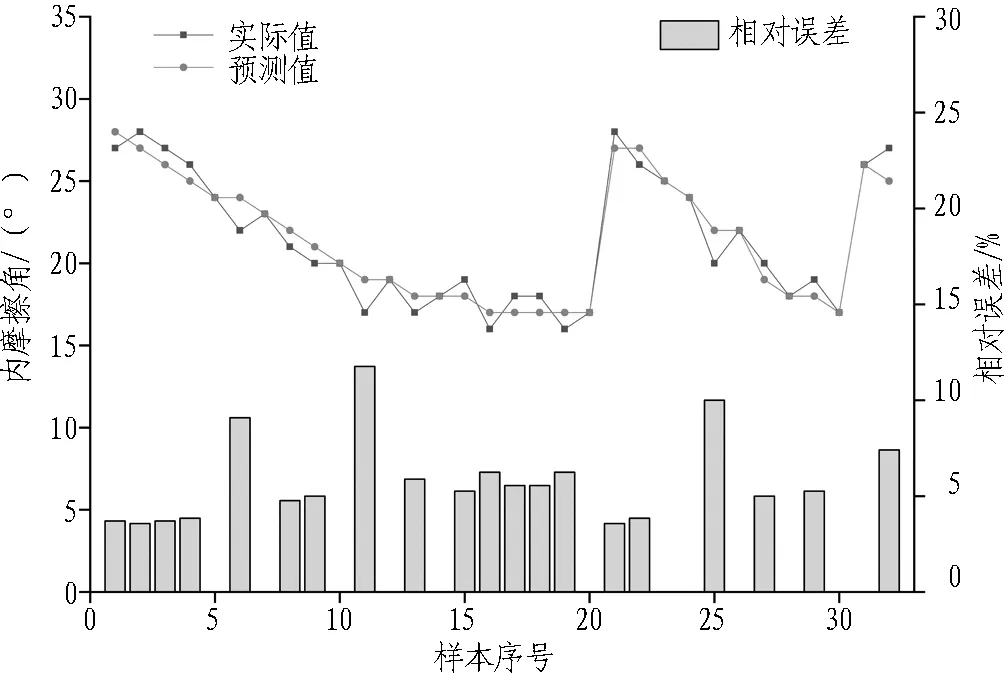
图9 内摩擦角的对比关系图Fig.9 Comparison of internal friction angle
在模型的整个构建过程中,坍落度、渗透系数和内摩擦角的相对误差最大值分别为5.36%、26.41%和11.76%,三者的平均误差分别为1.76%、4.53%和3.60%,误差结果表明该神经网络模型能够对富水砂层地区渣土改良效果进行精准预测。
为了更贴切现场渣土改良的实际质量分数配比,达到精准预测的目的,预测集中泡沫剂的质量分数范围为2%~5%,膨润土的质量分数为11%和13%。将预测集数据输入至符合精度要求的模型中,可以得到预测集的预测值及其相对误差,结果如表4所示。由表4可知:坍落度的预测值与实际值已实现大部分重合,最大相对误差为2.14%,平均误差为1.09%;渗透系数和内摩擦角的最大相对误差相对于坍落度而言较高,分别为10.73%和12.50%,但是平均误差分别为3.46%和4.23%。三者的平均误差均在5%以内,且渗透系数预测值的数量级与实际值相一致,表明本文所构建的神经网络模型能够对南昌富水砂层地区渣土改良试验进行精准的效果预测。

表4 预测值与实际值的误差对比Table 4 Comparison of slump,permeability coefficient and internal friction angle between predicted and actual values
4.2 优度检验
在检验预测效果时,通常使用统计学中的可决系数R2来评价BP神经网络模型对渣土改良的预测效果,即计算预测值的回归平方和与总体平方和的比值对样本预测值的拟合程度进行判定。对于可决系数R2,给出以下定义:
1)R2是在[0,1]区间内取值的非负系数;
2)R2=1说明预测效果最好,R2=0说明预测效果最差;
3)当0 可决系数R2可按下式计算: (9) 将坍落度、渗透系数、内摩擦角的预测结果代入式(9),可以得出三者的可决系数R2值分别为0.88、0.90和0.85,其预测效果按拟合程度从大到小依次为渗透系数、坍落度和内摩擦角。 将R2值与图7—9相结合可知,采用BP神经网络模型预测渣土改良后的坍落度、渗透系数、内摩擦角与实际值较为接近,3个性能指标的输出值均能达到现场试验所需的效果,说明该预测模型在实际工程中具有统计学意义,可以用此模型进行富水砂层地区渣土改良试验效果的预测。 1)本文基于BP神经网络建立了适用于富水砂层地区渣土改良试验的效果预测模型,通过学习过程中坍落度、渗透系数和内摩擦角预测值与实际值的趋势对比曲线和相对误差关系,验证了模型预测的准确性,表明该神经网络模型能够对富水砂层地区渣土改良效果进行精准预测。 2)坍落度的预测值与实际值部分重合,最大相对误差为2.14%,平均误差为1.09%;渗透系数和内摩擦角的最大相对误差分别为10.73%和12.50%,平均误差分别为3.46%和4.23%。三者的平均误差均在5%以内,表明本文所构建的神经网络模型能够对南昌富水砂层地区渣土改良试验进行精准的效果预测。 3)通过对预测结果进行优度检验,计算得出输出变量的可决系数R2值分别为0.88、0.90和0.85,可知此神经网络模型的预测效果较为理想,可为富水砂层地区运用此模型进行渣土改良效果预测提供理论参考依据。 4)由本文的分析结果可以得出所建立的BP神经网络预测模型具有较高的预测精度,下一步应将此预测模型推广至其他地质条件下的地铁隧道建设。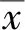
5 结论与讨论

