PPP轨道交通项目动态基准收益率研究

易 欣，喻 南，施晶晶，邱 慧

(1.中南林业科技大学土木工程学院，湖南 长沙 410004；2.中南林业科技大学风景园林学院，湖南 长沙 410004)

0 引言

我国轨道交通事业正蓬勃发展，为缓解资金压力和提高运营效率，PPP被越来越多地引入轨道交通项目。物有所值是评判PPP项目是否可行的重要依据，而基准收益率则是物有所值定量评价的核心参数。确定合理的基准收益率是吸引社会资本参与、确保项目公共属性的重要前提。我国PPP轨道交通项目尚无统一的基准收益率，这给物有所值定量评价带来极大困难，实践工作往往只能做定性评价或完全凭经验取值。因此，确定合理的基准收益率对PPP轨道交通项目前期决策意义重大。

国内外学者对基准收益率的研究方法主要包括社会折现率法(SDR)、德尔菲法、典型项目模拟法、加和法、加权平均资金成本(WACC)、资本资产定价(CAPM)法等[1-2]。由于典型项目模拟法受限于选取的项目数量，德尔菲法受专家主观判断影响大，目前CAPM法应用最广，但多用于证券投资领域。在PPP项目领域，秦旋[3]以CAPM法为基础构建了改进BOT项目特许期计算的模型。方俊等[4]运用CAPM法和WACC法给出了PPP综合管廊项目的多目标规划定价模型。综上，现有研究未能结合项目的行业特点分析其对基准收益率的影响，也未有效分析项目环境变化引起的基准收益率动态变化，大多采用固定基准收益率。本文将根据轨道交通的行业特点，考虑项目需求的不确定性，基于不同决策时机构建Vague集改进的CAPM模型研究PPP轨道交通项目动态基准收益率，以期为政府PPP轨道交通项目相关政策制定和社会资本的项目投资决策提供理论依据。

1 PPP轨道交通项目动态基准收益率理论分析

1.1 PPP轨道交通项目不同决策时机的概念

决策时机最初主要应用于企业投资和战略管理，Dixit等[5]最早研究了市场需求不确定对企业投资时机的影响。Ulrich等[6]认为决策时机是企业战略环境建模分析的重要组成部分。在PPP领域，Huang等[7]用复合期权分析了多阶段PPP项目的投资时机。张书华等[8]用最优多停时理论研究了PPP项目多阶段投资时机决策问题。PPP轨道交通项目投资大、不确定性强且具有突出的运营网络效应，也存在多阶段决策的特点。易欣[9]根据网络效应带来的客流可扩展性，将PPP轨道交通项目特许运营期划分为客流的吸引产生、培育发展和相对趋稳3个阶段。在此基础上，本文将3阶段理念扩展到整个轨道交通运营网络，并将项目的决策时机细分为网络形成前决策、网络形成时决策、网络形成后决策，而处于不同决策时机的轨道交通项目若考虑引入PPP模式，其相应的基准收益率应为一个合理的取值范围并有所差异，而非不变的固定值，具体描述如下。

1)轨道交通运营网络形成前决策。本阶段，城市即将或刚开始进行轨道交通建设，运营线路较为单一，与其他线路或公共交通工具的换乘网络尚未形成。此时若引入PPP模式，考虑到乘客对轨道交通尚处于尝试期，客流需要吸引和逐步产生，缺乏规模效应，运营成本较高，为了吸引社会资本，PPP轨道交通项目基准收益率在合理范围内可适当取高值。

2)轨道交通运营网络形成时决策。本阶段，城市的轨道交通运营线路已经达到4～5条，各线路间换乘站有3 座及以上，与其他公共交通工具接驳越来越便捷，运营网络已初步形成。此时若引入PPP模式，考虑到客流量快速增加、运营管理日趋成熟，规模效应逐渐显现，运营成本不断降低，社会资本的参与热情也会有所增加，PPP轨道交通项目基准收益率在合理范围内可适当取中间值。

3)轨道交通运营网络形成后决策。本阶段，城市的轨道交通运营线路已经达到一定规模，与其他线路或公共交通工具的换乘网络已较为完善。此时若引入PPP模式，考虑到客流量日渐趋稳、各类运营管理经验成熟，规模效应明显，边际成本不断降低，政府合作、相关制度和法律法规也更加完善，社会资本的参与热情明显，PPP轨道交通项目基准收益率在合理范围内可适当取低值。

1.2 PPP轨道交通项目动态基准收益率模型构建

1.2.1 CAPM模型理论

文献[10]在Markovitz投资组合理论的基础上提出CAPM模型，通过在行业内选取代表性企业样本，以若干年企业财务报表为基础数据，通过风险系数来测算行业基准收益率，计算公式如下:

R=Rf+βe(Rm-Rf)。

(1)

式中：R为项目权益资本收益率；Rm为市场投资平均收益率;Rf为无风险收益率;βe为投资项目的系统性风险系数，用来度量投资项目相对于市场平均风险的大小。其中,βe是其中关键变量，其计算公式如下：

(2)

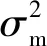
(3)

式中：βi为项目收益率平均值相对于整个市场组合的理想值；βi+1为项目收益率平均值相对于整个市场组合超前一期的观察值；βi-1为项目市场收益率平均值相对于整个市场组合滞后一期的观察值；βm+1为市场组合风险系数的观察值。

1.2.2 Vague集理论

与普通模糊集相比，Gau等[11]提出的Vague集对不确定信息的分析处理更准确，其定义如下。

1)定义1。设U是一个论域,x表示其中任一元素,U中的一个Vague集A可用一个真隶属函数tA和一个假隶属函数fA表示，tA(x)是从支持x的证据所导出的x的隶属度下界,fA(x)则是从反对x的证据所导出的x的否定隶属度下界,不确定部分为1-tA(x)-fA(x)。tA(x)和fA(x)将区间[0,1]中的实数与U中的每一个元素联系起来。即,tA(x):U→[0,1]，fA(x):U→[0,1]，为讨论方便,简记tA(x)为tx,fA(x)为fx。

当U连续时,Vague集A表示为

(4)

当U离散时,Vague集A表示为

(5)

式中：tA(x)+fA(x)≤1，令πA(x)=1-tA(x)-fA(x)表示不确定度。若tA(x)=1-fA(x)，则Vague集退化为普通模糊集；如果tA(x) 和1-fA(x)同时为 0 或 1，则Vague集退化为普通集合。

2)定义2。设A和B是U上的2个Vague集，其加法、乘法和数乘运算规则如下：

A⊕B=[min{1,tA+tB}],[min{1,(1-fA)+(1-fB)}]；

(6)

A⊗B={[tA(xi)·tB(xi)],[1-fA(xi)-fB(xi)+fA(xi)·fB(xi)]}；

(7)

k·A=[k·tA,k·(1-fA)],k∈[0,1]。

(8)

考虑到实际工作中的所有参数都为单值数据，在使用Vague集进行数值计算时，需要先把单值数据按照式(9)的方法转化为Vague值的区间数形式：

(9)

1.2.3 基于Vague集的改进CAPM模型

根据前述分析可知，处于不同决策时机的PPP轨道交通项目基准收益率不应为一个不变的固定值，而是合理的取值范围，即1个区间数，并能有效刻画项目中的不确定性信息，故本文提出了基于Vague集改进的CAPM模型，具体步骤如下：1)为使数据具有可比性并尽量保留数据包含的信息量，先按规范化原则对原始数据进行标准化处理；2)将处理后的数据根据式(9)转化为Vague值形式；3)将转化为Vague值的数据代入CAPM模型，依据式(6)、(7)和(8)运算规则，测算出PPP轨道交通项目基准收益率的合理取值范围。

1.2.4 基于WACC修正的PPP轨道交通项目基准收益率

由于直接套用CAPM模型得出的是项目权益资本收益率，而PPP轨道交通项目投资巨大，项目除权益资本外还因融资而产生债务资金，故测算项目基准收益率时还需综合考虑权益资本和债务资金各自的资金成本，采用WACC进行适当修正[12]，公式如下。

(10)

Kd=i(1-T)。

(11)

式(10)—(11)中：E为项目权益资本资金;D为项目负债资金;Kd为减去所得税后的负债资金成本;i为项目长期贷款利率;T为企业所得税税率25%。

2 样本数据的选取及处理

2.1 非系统性风险的数据来源

投资风险可分为系统性和非系统性风险，CAPM模型认为有效的投资组合可使投资者承受的非系统风险为零，故βe只考虑了系统性风险[13]。由于CAPM模型研究对象是证券市场的上市企业，其系统性风险只站在企业融资的角度，而PPP面向的是项目融资，来自项目内部的非系统性风险影响同样不容忽视。因此，本文提出非系统风险因素与系统性风险存在因果关系的假设，认为非系统性风险对项目基准收益率也有影响。为验证此假设，借鉴既有研究成果并结合轨道交通行业特点，从系统性和非系统性风险2方面识别出了影响PPP轨道交通项目基准收益率的主要因素[14-15],如表1所示。

表1 影响PPP轨道交通项目基准收益率的风险因素Table 1 Risk factors affecting benchmark rate of return of PPP rail transit project

2018年12月—2019年6月，以参与过PPP轨道交通项目的政府部门、轨道交通公司、设计、咨询、监理和施工单位管理和技术人员为调查对象，以表1的指标对基准收益率的影响因素进行调查，所有问题均采用里克特量表5点计分法。通过腾讯问卷平台共发放120份问卷，最终得到有效问卷98份，问卷回收率81.17%。对所有调查对象根据其从业性质、工作经验和项目经历等进行了初步统计，相关信息如表2所示。

表2 调查对象来源统计表Table 2 Statistics of respondent sources

结合调查数据，首先，对2个潜变量进行了信度和效度检验，得到Cronbach′sα值为0.973，再通过主成分分析得到各观测变量的因子载荷均超过0.7，表明量表的可靠性和观测变量的效度均较高。

然后,用AMOS软件构建了PPP轨道交通项目基准收益率的结构方程模型，结果显示模型的拟合指数CMIN/DF=1.632<5，表明模型与数据契合度良好；P=0.000<0.05表明初始模型达到了统计性的显著；RMR=0.063，GFI=0.695，RMSEA=0.081表明模型总体通过了检验。因此，上述分析表明影响PPP轨道交通项目基准收益率的系统性和非系统性风险因素之间存在直接因果关系，计算风险系数βe时应考虑非系统性风险因素的影响。在此基础上，进一步对影响因素进行主成分法分析并提取出5个主成分，依据其主要代表的风险因素进行命名：1)“政治环境因子”，反映影响项目基准收益率的政治环境因素；2)“经济环境因子”，体现经济环境对项目基准收益率的影响；3)“行业环境因子”，体现项目行业特点的风险因素;4)“运营管理因子”，反映项目运营管理状况对基准收益率的影响；5)“建设管理因子”，反映项目建设管理水平对基准收益率的影响。

最后，通过方差还可得到各主成分因子的权重。限于篇幅，具体计算过程不一一展示，仅将最终结果列出如表3所示。根据表3可知系统性风险对项目风险的贡献度为0.51，还有0.49来自非系统风险因素，则修正后的项目风险系数

表3 各风险因素权重表Table 3 Weight of each risk factor

(12)

2.2 系统性风险的数据来源

2.2.1 风险系数βe的数据来源

本文以2009年1月4日—2018年12月31日为样本区间，选取了上海股市中以轨道交通运营、建设、设备及研发等为主营业务的31家上市公司为研究对象，轨道交通主营业务上市公司净资产收益率如表4所示，利用其净资产(权益资本在上市公司发布的财务数据中称为净资产)收益率和加权净资产收益率来确定βe，2009—2018年所有上市公司加权净资产收益率如表5所示。

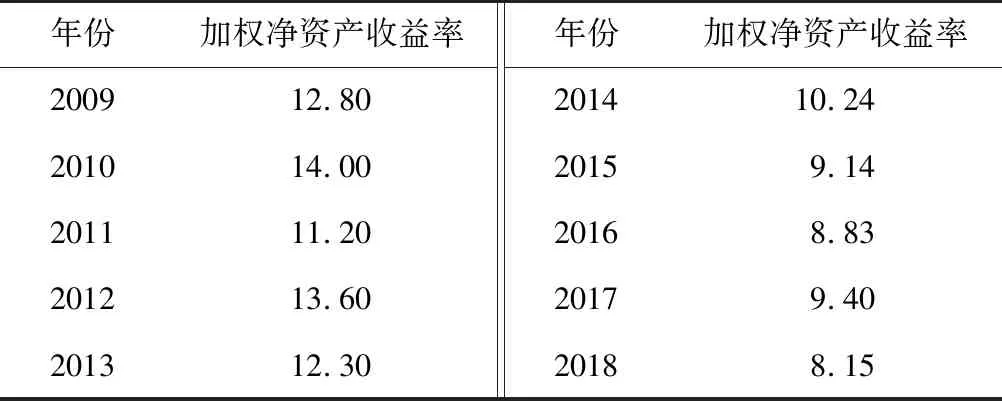
表5 2009—2018年所有上市公司加权净资产收益率Table 5 Weighted return on net assets by all listed companies from 2009 to 2018 %

表4 2009—2018年轨道交通主营业务上市公司净资产收益率Table 4 Return on net assets of listed companies with main business of rail transit from 2009 to 2018 %

2.2.2 无风险收益率Rf的数据来源

国际上通常以银行同业拆借利率来表示无风险利率，但目前我国利率尚未完全市场化，因此无法直接使用，故本文采用了2009—2018年的5年定期存款利率来计算无风险收益率(如表6所示)。

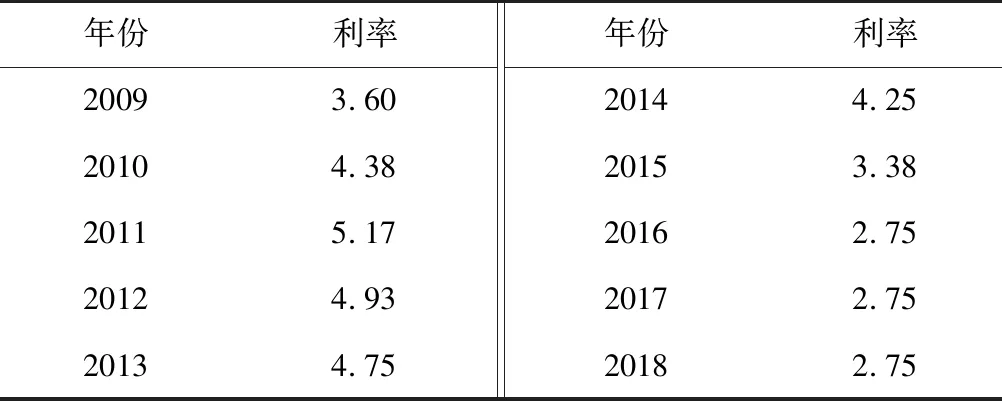
表6 2009—2018年5年定期存款利率Table 6 Five-year fixed deposit rate from 2009 to 2018 %

2.2.3 社会投资平均收益率Rm的数据来源

Rm反映的是市场平均收益率，其关键是确定市场组合。上证综指数能够比较准确地反映股票市场整体行情和整体发展趋势，可近似看作Rm。选择2009—2018年上证综指数据，上证指数收益率如表7所示。

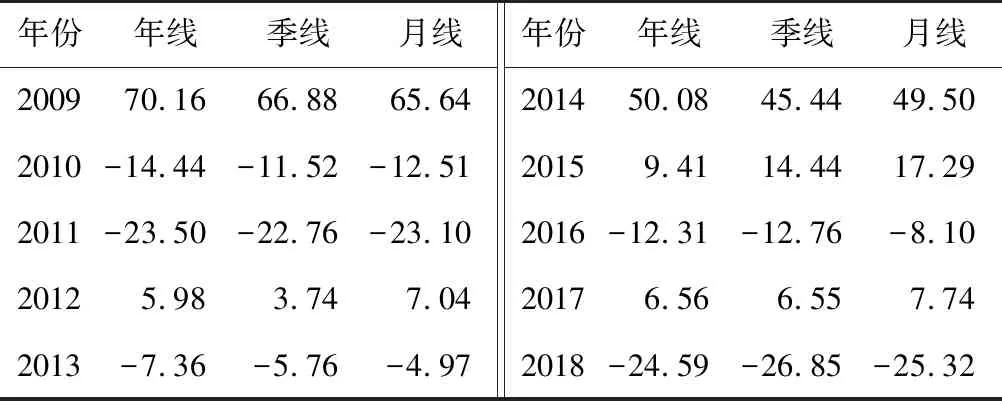
表7 2009—2018年上证指数收益率Table 7 Shanghai stock exchange index return rate from 2009 to 2018 %

采用式(13)计算相应的年线、季线及月线期望市场收益率来确定Rm。

(13)

式中：Rm(T)表示市场组合在T-1时刻到T时刻的收益率；Index(T)表示市场组合在T时刻的收盘指数；Index(T-1)表示市场组合在T-1时刻的收盘指数。

3 实证分析

长沙市轨道交通6号线PPP项目西起谢家桥站，东至黄花机场西站，全长48 km，设站34座，1个车辆段，1个停车场，3个主变电站，总投资约338亿元。按照规划分中、东、西3段分期实施并采用PPP模式建设，中段线路和西段路线均已开工建设，东段路线计划2020年开工建设。项目借鉴北京地铁4号线成功经验，PPP项目公司将承担机电设备工作并负责特许期的运营管理。目前6号线PPP项目正在公开招标，其中权益资本占比30%，债务资金成本为6%，采用上述思路对该项目基准收益率进行合理测算。

3.1 系统性风险系数βe的测算

表8 标准化后的净资产收益率Table 8 Standardized return on net assets %

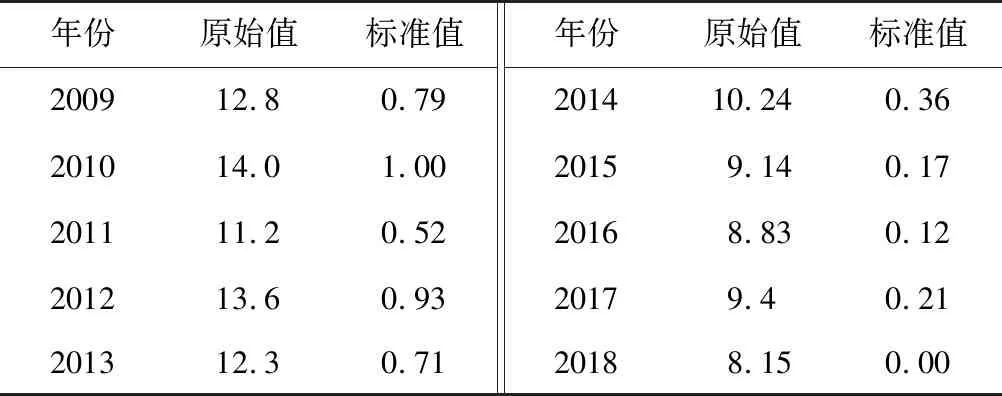
表9 标准化后的2009—2018年加权净资产收益率Table 9 Standardized weighted return on net assets by all listed companies from 2009 to 2018 %

表标准值Table 10 Standard value of

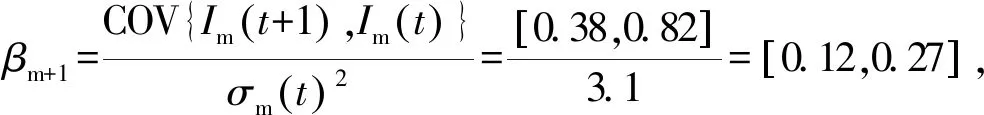
3.2 考虑非系统性风险影响的修正风险系数

根据表3和式(12)，求出修正后的风险系数

3.3 无风险收益率Rf的测算

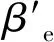
表11 2009—2018年5年期定期存款利率Table 11 Five-year fixed deposit rate with Vague set from 2009 to 2018 %

3.4 市场投资平均收益率的Rm测算

根据式(13)计算出表5中上证综指的年线、季线及月线投资平均收益率，再求三者的均值为7.47%，最后以区间数形式表达，即Rm= [0.074 7,0.074 7]。

3.5 PPP轨道交通项目基准收益率的初步测算

3.6 基于WACC的 PPP轨道交通项目基准收益率修正

根据式(10)和式(11)，求得WACC=0.3[0.051 2,

0.073 4]+0.7[0.06,0.06]=[0.057 3,0.064 0]。

根据结果可知本项目的基准收益率为5.73%～6.40%，比《建设项目经济评价方法与参数》(3版)提出的“对建设周期长的项目可在6%～8%的基础上适当提高的基准收益率的要求”偏低，但比国家发改委在发改投资[2013]586号文中公布的“铁路新建项目基准收益率3%和经营性公路项目5.5%”略高。考虑到颁布于2006年的《建设项目经济评价方法与参数》(3版)正值经济高速发展时期，社会折现率总体偏高。而目前我国宏观经济正处于结构调整时期，增速有所放缓，故测算结果基本符合当前实际。目前长沙市已运营的有轨道交通1、2、4号线，3、5号线2020年也将投入使用，轨道交通网络正在逐步形成。因此，根据前述分析可知本项目处于轨道交通运营网络形成时的决策，建议进行VFM定量评价时基准收益率可取中间值6.07%。若为了吸引社会资本参与本项目，政府也可以在与社会资本进行谈判的过程中根据实际情况适当提高，但建议不超过6.4%。未来长沙轨道交通网络将随着更多线路建设而趋于完善，如果其他线路也计划引入PPP模式，则应根据项目实际逐步降低基准收益率的取值。

4 结论与建议

目前针对PPP轨道交通项目基准收益率的相关研究和政策都还不够完善，本文根据轨道交通运营网络效应带来的客流可扩展性，将PPP轨道交通项目的决策时机分为网络形成前、形成时和形成后3个阶段，采用Vague集改进的CAPM模型研究了不同决策时机的PPP轨道交通项目动态基准收益率，得到以下结论：

1)影响PPP轨道交通项目基准收益率的因素包括系统风险和非系统风险，它们对风险系数βe取值的贡献度分别为0.51和0.49。

2)根据2009—2018年以轨道交通为主营业务的31家上市公司财务数据和中国人民银行同时段5年期存款利率，测算出PPP轨道交通项目基准收益率可在5.73%～6.4%根据决策需要合理取值。

3)实证分析验证了该模型的有效性，为政府在轨道交通领域引入PPP模式科学决策提供了参考。

本文对PPP轨道交通项目动态基准收益率的测算主要来自于31家上市公司公布的客观数据，未能完全考虑不同公司数据对结果影响的重要程度差异性，比如轨道交通建设、运营为主的公司应该比设备研发公司更为重要。另外，适度引入专家群决策对PPP轨道交通项目动态基准收益率进行主观预测，再将其与客观数据计算得出的结果进行有效耦合，可能会更贴近实际，这些都是下一步研究的方向。