基于元胞自动机的高温防护服厚度优化设计∗

李佳璐 陈雅颂 廉兴旺 李 政

(1.天津工业大学计算机科学与技术学院,天津 300387;2.天津工业大学数学科学学院,天津 300387;3.天津工业大学电气工程与自动化学院,天津 300387;4.天津工业大学物理科学与技术学院,天津 300387)

0 引 言

越来越多的工作者必须在高温环境下进行劳动,如冶炼操作人员和消防员等,高温环境下的应激问题成为人们普遍关注的问题[1].在高温环境中穿着高温防护服以降低皮肤表面温度,以此减少高温环境对工作效率的影响,因此高温防护服材料的参数设计显得尤为重要[2-3].

在一般高温防护服的设计过程中,将第Ⅱ层作为主要的吸热层[4],所用材料比热容较大,远远高于其他层,但与此同时材料密度也是其他材料的几到几十倍,如何设计出既满足吸热能力要求,又不至于质量太大影响工作活动的第Ⅱ层衣物厚度,是高温防护服参数研究过程中的重要课题.因此结合实际情况建立有效的热传递模型,根据相应的温度和质量等约束条件,准确方便地求解出高温防护服材料的衣物厚度参数,并检验参数的稳定性,具有很高的研究价值.

1 模 型

本文测得环境温度为75℃,工作时间为90 min时,皮肤表面温度与时间关系的实验数据.根据相关文献可知[5],高温工作者在环境温度为65℃,工作时间为60 min的条件下,皮肤表面温度一般不超过47℃,且超过44℃的时间不超过5 min,否则身体会出现不适.因此本文将探究在此种情况下第Ⅱ层衣物的最优厚度.

Torvi[6]利用有限元法求解高温环境中皮肤表面温度,但因为变量较多,边界条件复杂,导致求解困难,甚至难以求出最优解;Song等[7]使用有限差分法建立了织物-空气层-皮肤系统微分方程,但是非线性问题的差分法求解仍然是十分困难的.本文选取元胞自动机进行仿真模拟[8],其具有极强的仿真能力,而且求解简单易行,能很好地模拟高温防护服层与层之间一系列温度迭代规则,充分考虑现实情况中的人体高温防护,从而使模型更加贴近实际,通用性强.

元胞自动机可将空间和时间进行离散化处理,有别于其他动力学系统之处在于其用一系列模型构造规则形成,没有严格定义的函数或物理方程[9].散放在规则网格中的每个元胞都存在有限的离散状态,遵从相同的运动规则.根据局部规则同步更新,每个元胞所处的状态由自身和邻近元胞所决定.

一维元胞自动机是最简单的元胞自动机[10],邻域半径(r)为1,状态个数(z)为2,所以其状态集只包含2个元素,存在局部映射g:Y3→Y,其中Y3表示,Y表示,则有表达式

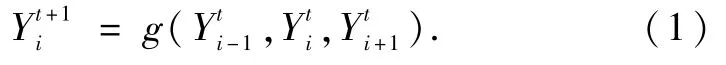
以下映射表示元胞的1个规则,如图1所示.

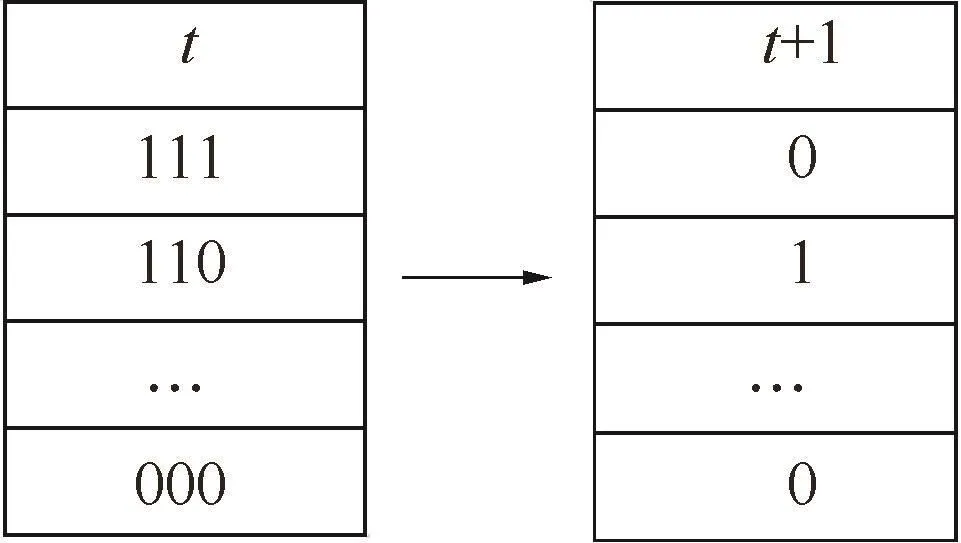
图1 元胞状态转换

一维元胞自动机状态集包含{y1,y2}2种状态,本文将原有的一维元胞自动机模型加以改进,将各层温度离散化,由于衣服各层厚度较小,均 ＜15.0 mm,用各层温度的平均值近似代替该层温度来表示元胞的状态.根据高温防护服的防护过程,将衣服各层看成1个完整的元胞,可得每个元胞的运动规则:

①所有元胞都处于一维网格中;

②元胞状态考虑左右2个邻居,取固定边界条件;

③遵循一定的温度更新规则.

基于传热学理论建立了以第Ⅱ层最优厚度为目标函数的优化模型[11],最终通过元胞自动机模型求解第Ⅱ层最优厚度,并通过灵敏度检验分析了该模型的合理性和有效性.

2 传热学理论介绍

由于织物-空气层-皮肤系统遵循能量守恒定律[12],所以根据流经、流入和流出系统的热量,可以得出整体温度变化与皮肤表面温度和时间的关系.热交换过程中,存在传导、对流和辐射3种热交换方式,由于在一定时间内存在恒温现象,所以第Ⅱ层作为吸热层会吸收大量热量.

2.1 传导换热量的定义及计算

依靠分子和原子等微观粒子的热运动产生的热传递称为传导性传热,通过传导性传热传递的热量是传导换热量[13],傅里叶定律能够很好地解释该热量交换过程[14].

3层衣物内部传导属于一维多层平壁稳态热传导[15],平壁面积与平壁厚度之比极大,可以忽略平壁边缘热损,平壁温度随时间没有变化,只沿垂直于平壁方向线性变化.多层平壁热传导过程如图2所示.

傅里叶定律表示为[16]

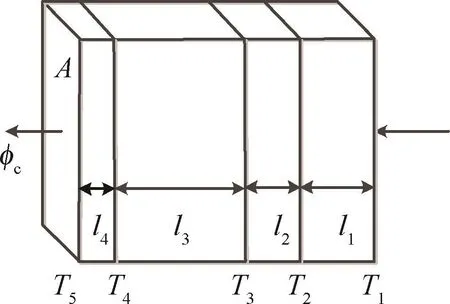
图2 多层平壁热传导

式中φc表示热流密度,λ表示热导率,T表示平壁的温度,x表示在导热平面上的坐标.由于每一层材料不同,所以热导率不同,但各个复合层的传热面积(A)相同,单位时间内一定面积的导热速率用qc表示,则

每层衣物内部温度的线性变化曲线如图3所示.x=0时,温度为T,x=l时,温度为T′,且T′＞T,因为A均为常量,则

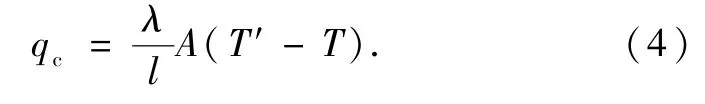
图3 温度线性变化曲线

2.2 对流换热量的定义及计算

对流换热是指流体经过固体时二者表面之间的热量传递现象,流体各部分因温度引起的密度差所形成的运动称为自然对流.本文流体是空气,所以空气流动过程中热传递的热量为对流换热量[17],牛顿冷却定律给出了对流换热量的计算方法.

根据牛顿冷却定律[11],当物体与周围存在温度差时,单位时间内通过单位面积交换的热量与温度差成正比,因此单位时间内通过一定面积的自然对流换热速率(qd)为

式中hc为对流换热系数,Tf表示温度高处一侧的温度,Te表示温度低处一侧的温度.

2.3 辐射换热量的定义及计算

物体因为温度原因以电磁波形式向外辐射能量,物体之间吸收辐射能并在相互辐射的换热过程中传递的能量为辐射换热量[17].在热辐射分析中,把光谱吸收比与波长无关的物体称为灰体[18],假定研究对象均为灰体,可以计算出衣物与空气层之间和皮肤表面与衣物之间的辐射换热量,因为皮肤表面与衣物之间的辐射换热量较小,忽略此部分热量.

单位时间内2灰体之间的辐射换热量(q1-2)为

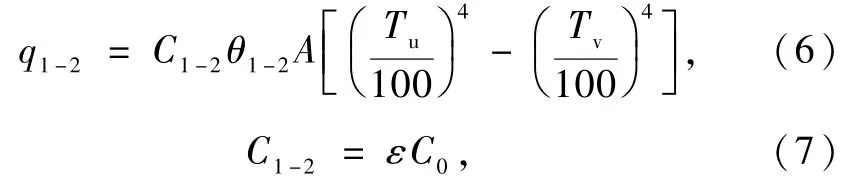
式中辐射角系数(θ1-2)为1.0,发射率(ε)为0.1,灰体辐射系数(C0)为5.67,A为传热面积,Tu和Tv为2灰体的温度,C1-2为1到2的总辐射系数.因此可得对流-辐射联合表面传热损失量(q)为

式中αT为对流-辐射联合表面传热系数,qD为对流换热量,qR为辐射换热量,TW为外界温度,T为衣服最表面温度.对于一维多层平壁[1]

2.4 吸热层吸热能力的计算

热传递过程中[19],忽略皮肤和衣物最内层之间的辐射热量,考虑对流、传导和辐射3种方式的热交换.4层衣物(包括最内层衣物)与皮肤表面之间的空隙划分为4层,其与外界空气进行热交换的过程如图4所示.

图4 热交换过程

从空气向第Ⅰ层织物传热,第Ⅰ层织物向第Ⅱ层织物传热,正向计算第Ⅱ层向第Ⅲ层的传热量,反向同样可以由Ⅳ层推导出Ⅲ层向Ⅳ的传热,同理,推出第Ⅱ层向第Ⅲ层的传热量.计算正反2侧第Ⅱ层向第Ⅲ层传热的温度差,即为第Ⅱ层织物的吸热量,因此可以计算每一时刻第Ⅱ层的吸热量.

3 第Ⅱ层最优厚度模型的建立

在避免灼伤的情况下,衣服厚度值应该越小越好,因此最优厚度为第Ⅱ层衣物的最小厚度值.设目标函数为第Ⅱ层衣物厚度值最小

约束条件1:时间约束.

在一般高温作业中环境的平均温度约为65℃,劳动时间平均1 h左右,必须保证假人在穿着高温防护服时皮肤表面温度在44℃ ＜T≤47℃的时间≤300 s[8].

(1)＜44℃的时间约束条件为

式中t1为假人皮肤表面温度＜44℃的时间,ta为假人皮肤表面温度＜44℃的最短时间,取

(2)在44～47℃的时间约束条件为

式中t2为假人皮肤表面温度在44～47℃的时间,tb为假人皮肤表面温度在44～47℃的最长时间,取

(3)总时间约束条件为

式中tc为假人穿着高温防护服在高温环境中的最短时间,取

约束条件2:第Ⅱ层衣物厚度约束条件为

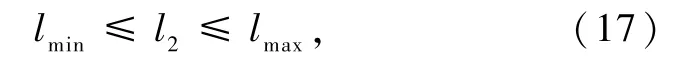
式中lmin=0.6 mm,lmax=25 mm[20].

综上所述,建立以第Ⅱ层最优厚度为目标函数的优化模型,其目标函数minl2的约束条件为

4 元胞自动机模型求解方法

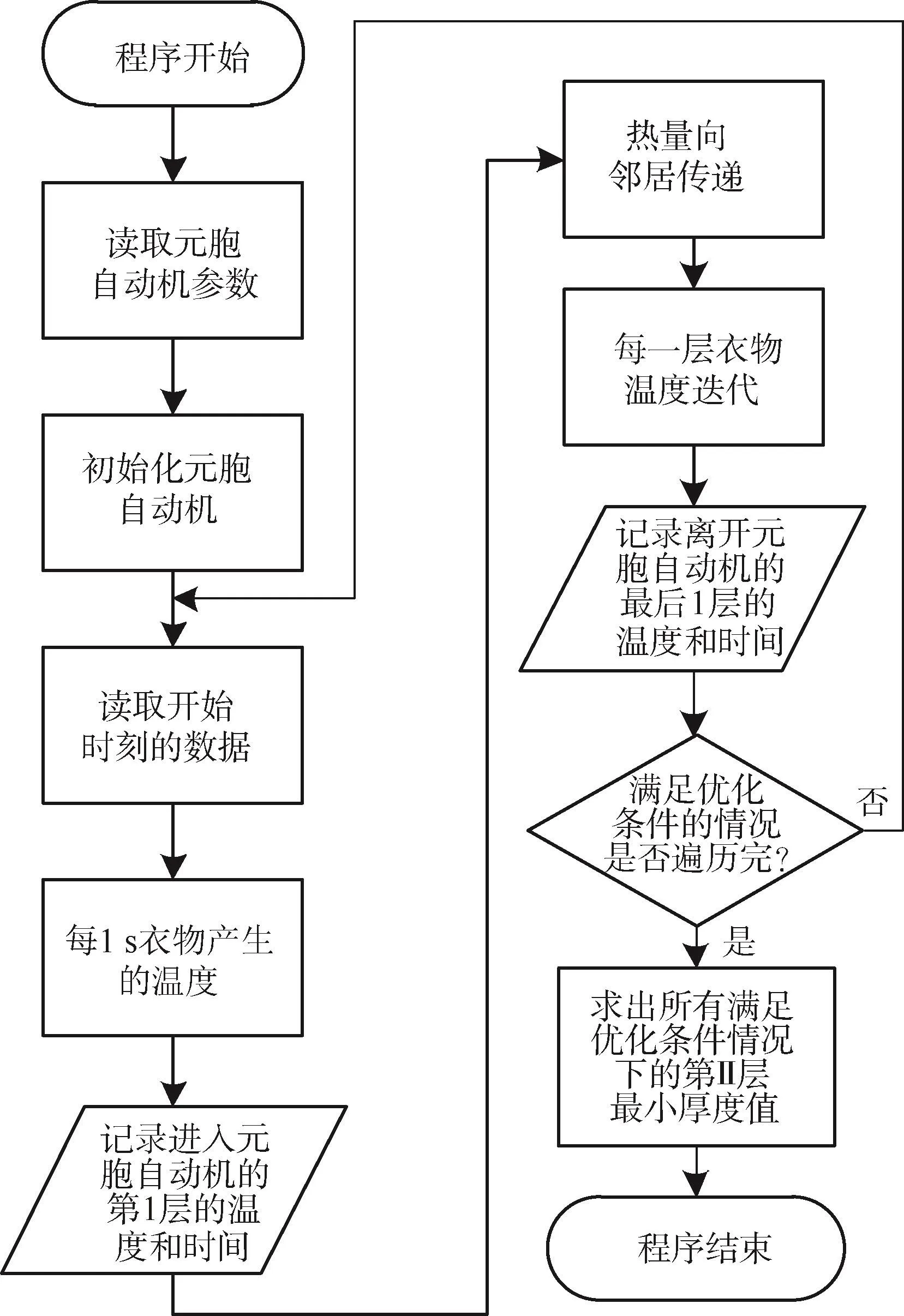
图5 循环遍历算法的仿真流程

(1)初始化元胞状态.

设定变量t来记录经历的时间,初始时刻(t)为

初始温度(Ti)为

将第Ⅱ层最优厚度初始化为l2的最厚厚度,即

(2)计算热量传递值.

计算每个元胞之间因温差传递的热量值,第i个元胞向它相邻的第i+1个元胞传递的热流密度(φi)为

计算人体表皮层在相邻时间因温度改变所形成的热流密度和衣服最外侧与外界空气温度所形成的对流-辐射联合表面传热速率(φ5与φ1)分别为

(3)劳动定额的确定。①充装工的工作班制：每周5天。主要工作内容：完成大瓶手工充装。计算方法如下：额定时间=标准时间*(1+宽放率)=52.55*(1+15%)=60.43，每班定编=每班总工时/可用工作时间=额定时间*频次/可用工作时间=(60.43*400/60)/410=1。

式中T4表示第Ⅲ和Ⅳ层之间的温度,T5表示人体表皮温度,T0表示外界空气温度,T1表示衣物表面温度.可求单位时间内人体皮肤温度上升所吸收的热量.每一层初始时刻吸收的能量(qi)为

对于间隙层,根据能量守恒定律既要考虑前一层给其传递的热量(q),还要考虑其传递给后一层的热量(q′)和其自身温度上升的热量(qs),所以三者有以下关系:

除了第Ⅱ层有较强吸热能力外,其他层的热量流向均类似于间隙层.在第Ⅱ层时,还要考虑第Ⅱ层吸收的热量(qx),则有

(3)温度迭代规则.

除了第Ⅱ层的其他层:设现在该层的温度为T0,下一时间节点的温度(Tx)为

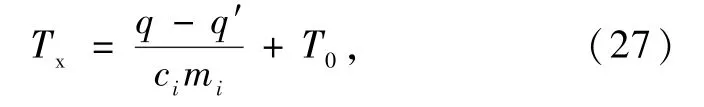
式中ci和mi分别表示第i层的比热容和质量.

第Ⅱ层:设现在该层的温度为T0,则Tx为

(4)循环遍历.

第Ⅱ层的厚度遍历范围为0.6～25.0 mm,选取步长为0.1 mm进行循环遍历,时间步长为1 s,在满足第Ⅱ层厚度最优模型的前提下,如果l′1＜l1,则

反之,l1保持不变.

(5)结束标志.

第(4)步结束后,输出l1.

5 仿真实验

根据环境温度为75℃,工作时间为90 min时的假人皮肤表面温度与时间关系的实验数据,求出第Ⅱ层织物每一时刻的吸热量,用Matlab的cftool工具箱进行拟合,得到拟合曲线方程为

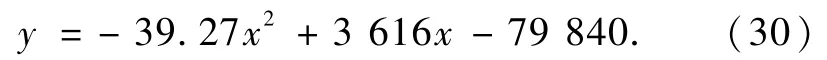
理论值和实验值相对误差率约为1.03%,方程拟合效果较好(图6).吸热层的吸热量随时间变化的趋势可以得到:从37℃开始,吸热能力逐渐加大,直到大约46℃ 时吸热层吸热能力达到最大,之后开始减少.

图6 吸热层吸热量变化

利用元胞自动机模型求解出皮肤表面温度的模拟值和实验测得的值随时间变化的对比曲线,如图7所示.只有升温过程中温度存在微小差距,且总体误差率≤1.20%,表明模型拟合效果较好.

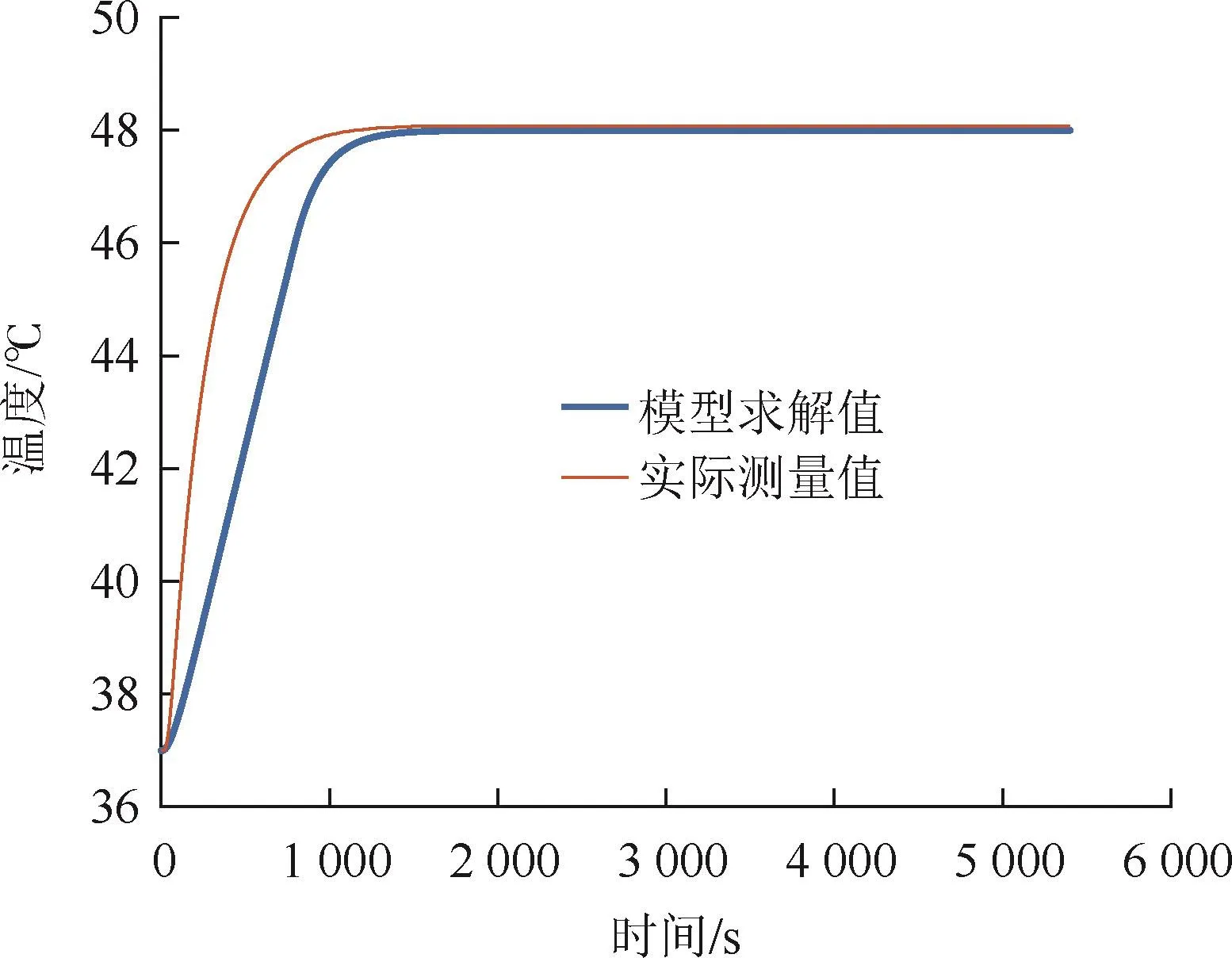
图7 假人皮肤表面温度真实值和模拟值对比

利用Matlab编程循环遍历结果可知:第Ⅱ层的最优厚度为10.3 mm,人体皮肤温度达到44℃的时间为3 320 s,皮肤温度在44～47℃的时间为280 s,皮肤能达到的最高温度为44.08℃.人体皮肤温度随时间的变化曲线如图8所示.

在外界温度为65℃的情况下,第Ⅱ层厚度在10.3 mm周围以±0.2 mm变化时,记录每一种厚度对应的皮肤温度达到44℃所需要的时间和皮肤达到的最高温度,以此来检验结果的稳定性.灵敏度检验结果如表1所示.可知,在环境温度为65℃的情况下,当第Ⅱ层厚度在10.2～10.4 mm变化时,皮肤温度达到44℃的时间均为3 320 s左右,且皮肤能达到的最高温度也满足＜47℃.

图8 人体皮肤随时间的变化曲线

表1 灵敏度分析

对于不同的第Ⅱ层厚度,其皮肤表面温度的灵敏度分析如图9所示.

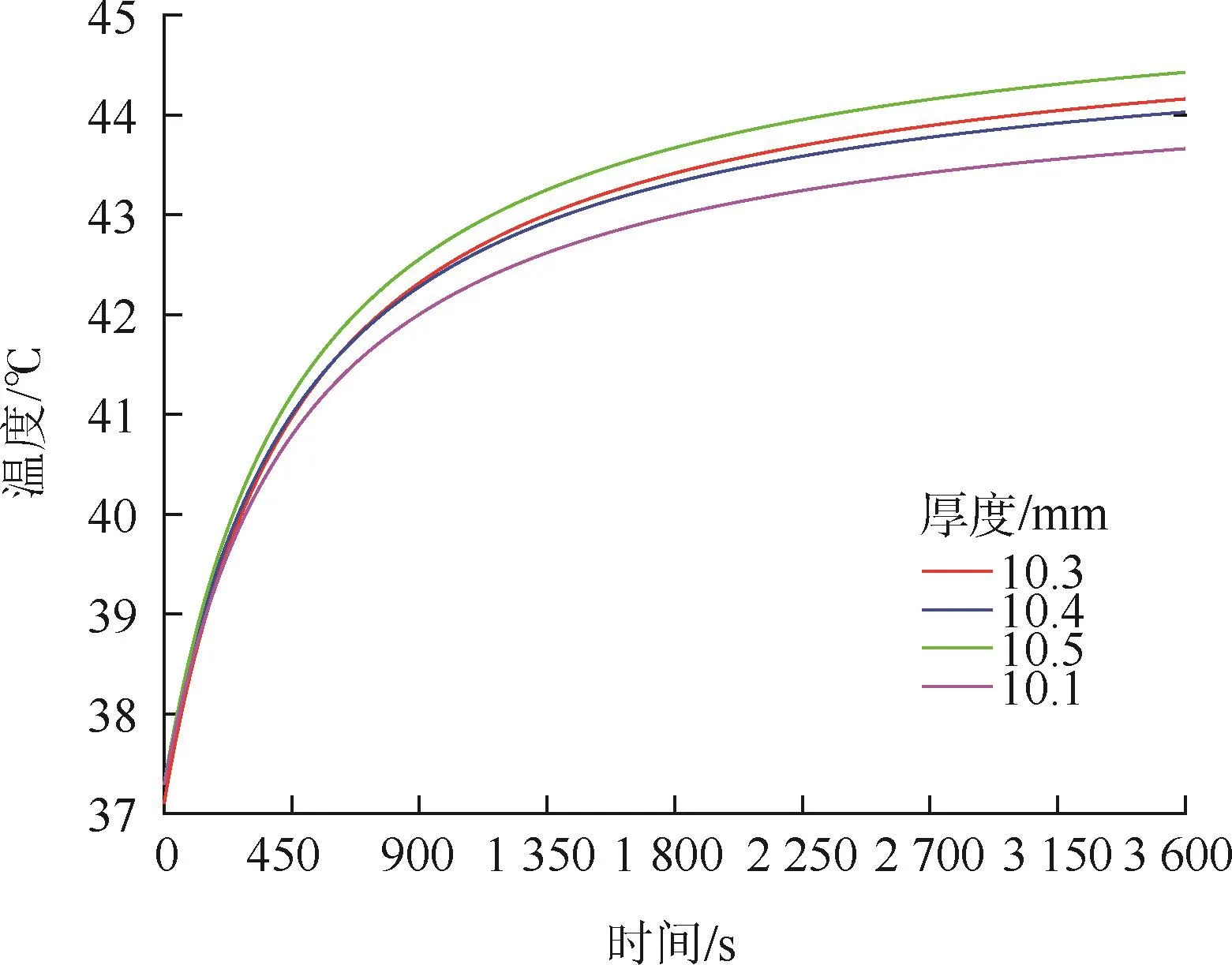
图9 灵敏度检验

6 结 论

本文通过元胞自动机对高温防护服第Ⅱ层厚度优化模型进行求解,得到高温防护服第Ⅱ层最优厚度.元胞自动机模型不仅适用于高温防护服的防热能力设计,还可以用于求解消防服的防火能力、超低温的抗低温能力和交通流等方面.把元胞自动机模型推广到二维、三维时还可以用于求解地壳热传导等空间立体的课题,具有很强的实际意义和广泛的应用空间.