随机生产下零售商二次降价的供应链协调模型∗

王 宁 胡 飞

(天津大学数学学院,天津 300350)

0 引 言

制造商和零售商之间的协调是供应链管理中的一个重要决策.在供应链协调下,制造商和零售商通过设置适当契约参数使得双方利益均达到集中模型下的最优值.各种各样的合同被广泛地运用到供应链协调中,如收益共享合同和数量折扣合同等.因为单一的传统合同并不能解决所有供应链的协调问题,所以越来越多的学者开始注重混合合同的重要性.

很多学者在不同的条件下拓展传统契约使供应链达到协调.Taylor[1]表明在需求受到零售商销售努力的影响下,设计合理的回扣和退货合同可以达到协调和双赢的效果.He等[2]探究了在随机需求下供应链的协调问题,表明当需求受销售努力和销售价格同时影响时,传统的契约并不能使供应链达到协调,但基于退款惩罚的退货契约能够使供应链达到协调.Hu等[3]基于产出和需求双重不确定的情况下,提出了1种弹性订单策略来分担随机产出给供应商带来的风险.He和 Zhan[4]提出了1个基于批发价合同的新型退货契约使得供应链达到协调.Pang等[5]在三级供应链中提出了1项基于回扣和惩罚政策的收益共享合同来实现协调.

在很多生产过程中,产品的产量并不确定,受很多因素的影响.如天气可以影响农作物的收成等.由于交通运输受多种灾害的影响,所有的交通运输过程都可以看做随机生产过程[6].Mukhopadhyay和Ma[7]在3种不同的情况下,提出了1种基于不确定需求和随机生产的最优采购和生产策略.He和Zhang[8]提出了几种分担随机产出风险的方法,并比较了不同方法的优劣.He[9]在闭环供应链中,分析了不同的供应链风险分担契约,通过理论分析和算例说明,不同的供给风险分担契约可能导致回收价格决策和再制造产量决策偏离集中回收结构下的决策.

随着市场竞争的激烈化,零售商通过下调价格来占据市场份额,零售商二次降价销售成为当前市场的常见现象,基于零售商二次降价的供应链协调模型更是供应链研究的热点话题.华晴云[10]考虑了在二次降价销售中的最优生产策略,但没有考虑契约模型下的协调问题.刘海军和陈菊红[11]考虑了基于零售商二次降价的回购契约协调供应链的条件.周海坚[12]在二次竞争降价销售下,研究了批发价契约、回购契约及回购加补贴契约的协调情况.

本文研究的是在降低随机产出风险的情况下,考虑零售商二次降价的两级供应链的协调问题.制造商和零售商都是风险中性并且以最大化各自的利益为目标.制造商和销售商通过协商制定了1个弹性订单策略来降低随机生产所带来的风险,在此基础上,本文讨论了如何制定契约使供应链在二次降价销售过程中达到协调.

1 模型描述和符号说明

本文所研究的销售期共分为2个阶段.在第1个阶段,零售商原价销售,每一个消费者对产品价值有1个随机的估计值V,假设消费者是理性的,即当产品的效用剩余＞0时,消费者才会购买,以此得到第1阶段的销量;在销售的第2个阶段,零售商采取降价销售,降价销售会给产品带来1个附加的购买效应,假设第2阶段的消费者同样是有限理性且与第1阶段的消费者不重合,即不会重复购买,那么会得到第2阶段的产品销量.

假设消费者对产品价值的估计值为随机变量V,服从分布函数为F的随机分布.第1销售阶段(原价销售阶段)的产品价格为p1,第2销售阶段(降价销售阶段)的销售价格为p2,且p1＞p2＞0.那么,消费者在第1阶段的消费剩余为V-p1,当消费剩余＞0时,消费者会购买产品,即V-p1＞0,那么,第1阶段的销量为

式中D1={v|v-p1≥0,v＞0}.

在产品销售的第2阶段,由于产品降价,消费者对产品的估值上会额外附加1个因为产品降价产生的交易效用.假设交易效用与降价幅度呈正比,即设

式中γ表示消费者对价格变化的敏感系数,0＜γ＜1.消费者在第2阶段的消费剩余可表示为V+γ(p1-p2)-p2,所以第2阶段消费者购买产品的必要条件为V+γ(p1-p2)-p2＞0.

假设第1和2阶段的消费者不重合,那么第2阶段产品的销量可表示为

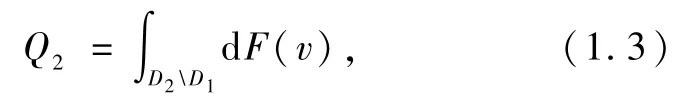
式中D2={v|v+γ(p1-p2)-p2≥0,v＞0}.

本文继续沿用 Chiang等[13]的假设,设随机变量V服从U[0,1],即V的最大估值为1.当p1＞1时,即此时第1阶段销售价格高于所有消费者的最大估值,认为这个价格是不合理的,因此p1的合理定义域为[0,1].

由以上假设,可以计算得出第1和2阶段的销量分别为

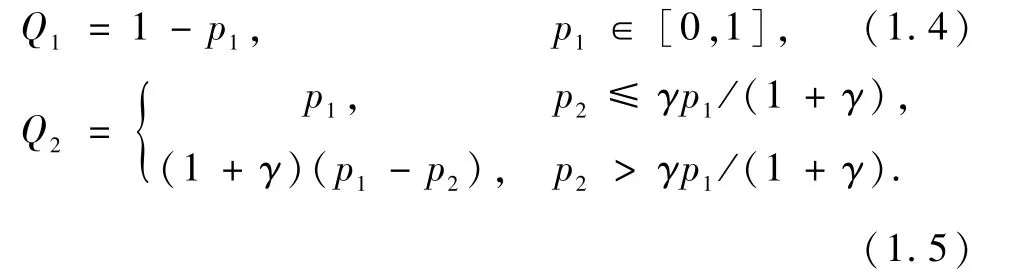
可以直观得出在p2≤γp1/(1+γ)条件下,总订单为1.该情况下不管价格如何调整,销量是不变的,认为在此基础上的研究没有意义.因此,在接下来模型中,讨论的订单销量均是在条件

p2＞γp1/(1+γ)

下进行的.

2 集中模型

在零售商二次销售模型中,零售商先将订单(Q1,Q2)提供给制造商,制造商根据订单确定生产总量L,制造商的生产成本为c,假设生产率θ是随机的,其随机变量的概率密度函数和分布函数分别是f(·)和F(·),且随机变量的期望已知为μ.制造商的实际供货量θL可能＞(Q1+Q2),也可能＜(Q1+Q2).因此,制造商提出了1个弹性订单策略来降低随机生产的风险.制造商在观察了零售商制定的订单之后,制造商制定了1个最低供货阙值Q1,制造商最少要满足零售商第1阶段的订单,如果θL＜Q1,那么制造商将以每单位ce的成本采取紧急生产.在这里,假设紧急生产的产率是完美的;如果θL＞Q1,小于总订单,那么零售商将接受实际供货量;如果θL大于总订单,那么产品将以每单位s的价格剩余.

基于以上模型,首先讨论在集中模型下的最优决策,供应链的总期望利润是由制造商和零售商各自的期望利润函数组成.则该集成式供应链的总利润函数为

式中Q1和Q2分别由式(1.4)和(1.5)给出.

对目标函数求一阶导数为

定理1对于给定的,在集中式供应链模型中,整个供应链的ΠC是关于L的凹函数,且最优的总生产量LC满足

证明对目标函数求一阶导数可得:

则目标函数关于L是凹函数.最优L可以通过求解目标函数的一阶最优性条件得到.

3 分散模型

3.1 非合作的Stackelberg博弈模型

制造商和生产商作为独立个体,将会以最大化自身的期望利润为目标,而忽略了供应链整体的利益.将分散模型当作 Stackelberg博弈,其中,制造商是主导者,零售商是跟随者,利用 Stackelberg逆向归纳法,先求解零售商的最优解.零售商的总利润函数为

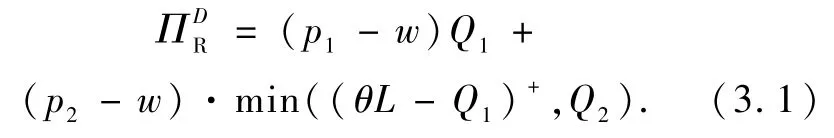
制造商的总利润函数为

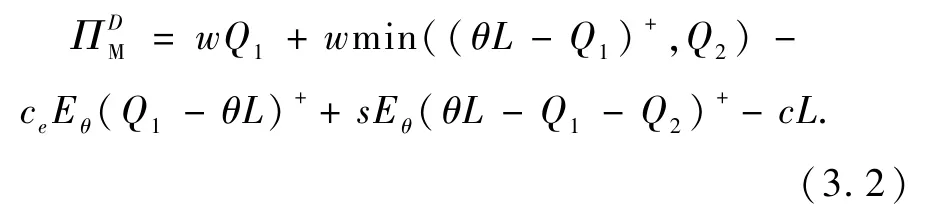
定理2在非合作的分散式供应链模型下,对于任意给定的L＞0,零售商为最大化自身利润,最优定价应同时满足

证明在Stackelberg博弈中,零售商的期望函数的一阶导数和二阶导数为

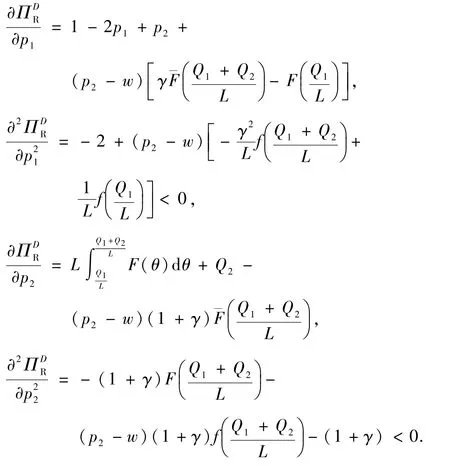
可以得知,使利润函数达到最优值的解是边界点或者是平稳点,可知边界点并不能使利润函数达到最大,因此,平稳点是最优解.即满足平稳点应同时满足目标函数的一阶最优性条件.

定理3制造商的利润函数是关于L的凹函数,其中最优总生产量LD满足方程

证明对分散模型下制造商的利润函数求关于总生产量的一阶导数

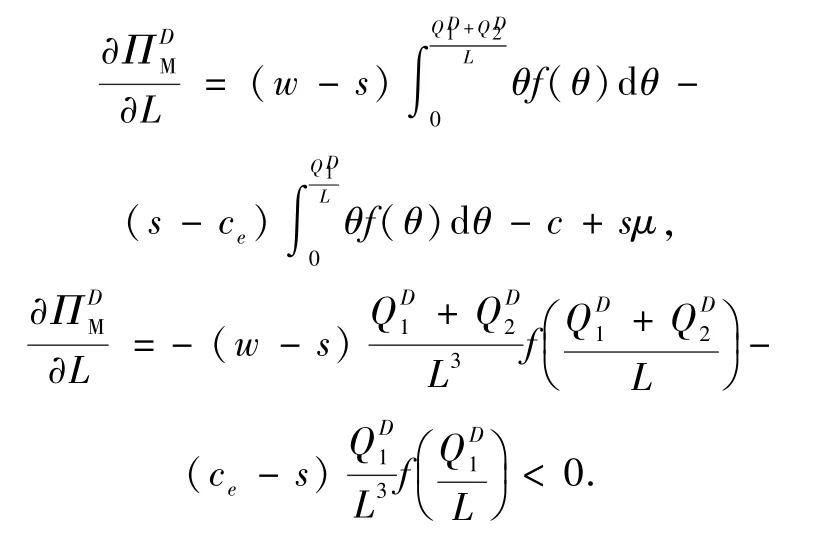
则目标函数关于L是凹函数.LD可以通过求解目标函数的一阶最优性条件得到.比较式(3.5)和式(2.2)直接得出,非合作的分散式供应链并不能达到协调.

3.2 基于惩罚退款的收益共享契约

研究显示,常规的供应链契约并不能使基于随机产出风险分担的两级供应链达到协调,在原有的利益分享契约上进行改进创新,提出了1种基于惩罚退款的收益共享契约.制造商设置了1个目标K,其中.为了促使零售商接受收益共享契约,本文提出了2种惩罚和退款形式,当制造商的实际供货量＜K时,制造商将给零售商δ1(K-θL)+的惩罚,又因为制造商的最低供货量是Q1,那么惩罚不超过δ1(K-Q1)+.同时,对于订单＞K的部分,制造商将会给零售商δ2(Q1+Q2-K)+的退款.令ρ(0＜ρ＜1)作为收益共享契约的参数,先得到零售商的期望利润函数为

对比集中模型下的最优解,可以得出当契约参数满足以上条件时,集中模型下的最优解与收益共享契约的最优解相等.

命题1假设定理4和5均满足,那么新型收益共享契约能够协调供应链.

制造商所提出的契约是收益共享契约和惩罚退款契约的结合,这个契约是由(δ1,δ2,K)3个参数构成,K不仅平衡了制造商对零售商的惩罚退款,还促使制造商做出与集中模型下相同的最优生产决策;同理,通过适当地调节参数(δ1,δ2),使零售商做出与集中模型下相同的最优决策.

由命题1可知,当供应链达到协调时,制造商和零售商的期望利润函数由以下公式可得:

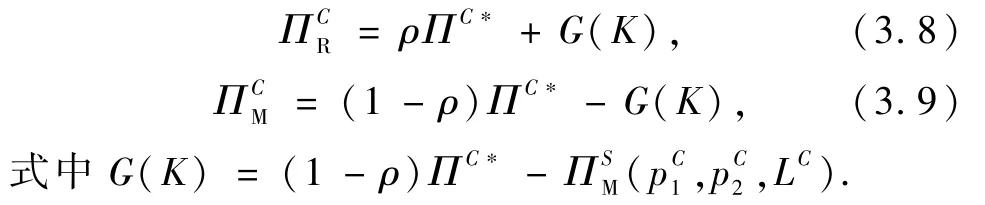
命题2在新型收益共享契约能够使供应链达到协调的前提下,当G(K)=0时,通过改变参数ρ可以实现对最优供应链利润的调节.

4 数字实例

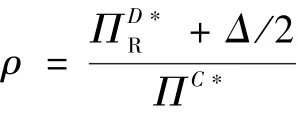
在新型共享利益契约下,供应链可以达到协调(表1).分析了在γ=0.3下,随机生产分布的不同对最优决策和利润的影响,当分布方差不同,期望相同时,分析随机分布处于U(0.2,1.2)和U(0.4,1)下最优值的变化,在集中模型中,期望相同,方差越小,利润越大,这与事实相符;当随机生产的变化幅度偏小时,风险更小,供应链的利润更高.当分布的方差相同、期望不同时,随机变量的期望越大,在集中模型中供应链的整体利润越大,在分散模型中,制造商的利润在方差不变的情况下,与期望的变化成正比.

表1 不同分布下供应链的最优决策和最优利润

在随机分布为U(0.2,1.2)时,各个利润函数随价格敏感系数的变化趋势见图1,由图1可知集中模型的总利润与价格敏感系数成正比,同时也表明制造商和零售商的利益在协调契约的影响下,得到明显提高.在随机分布为U(0.2,1.2)时,弹性订单合同对总体供应链利润的影响见图2.表明了在集中模型下,弹性合同下的利润增长率随价格敏感度的变化曲线.可以直观感受到弹性订单合同能够增加供应链的期望利润,降低随机生产风险.

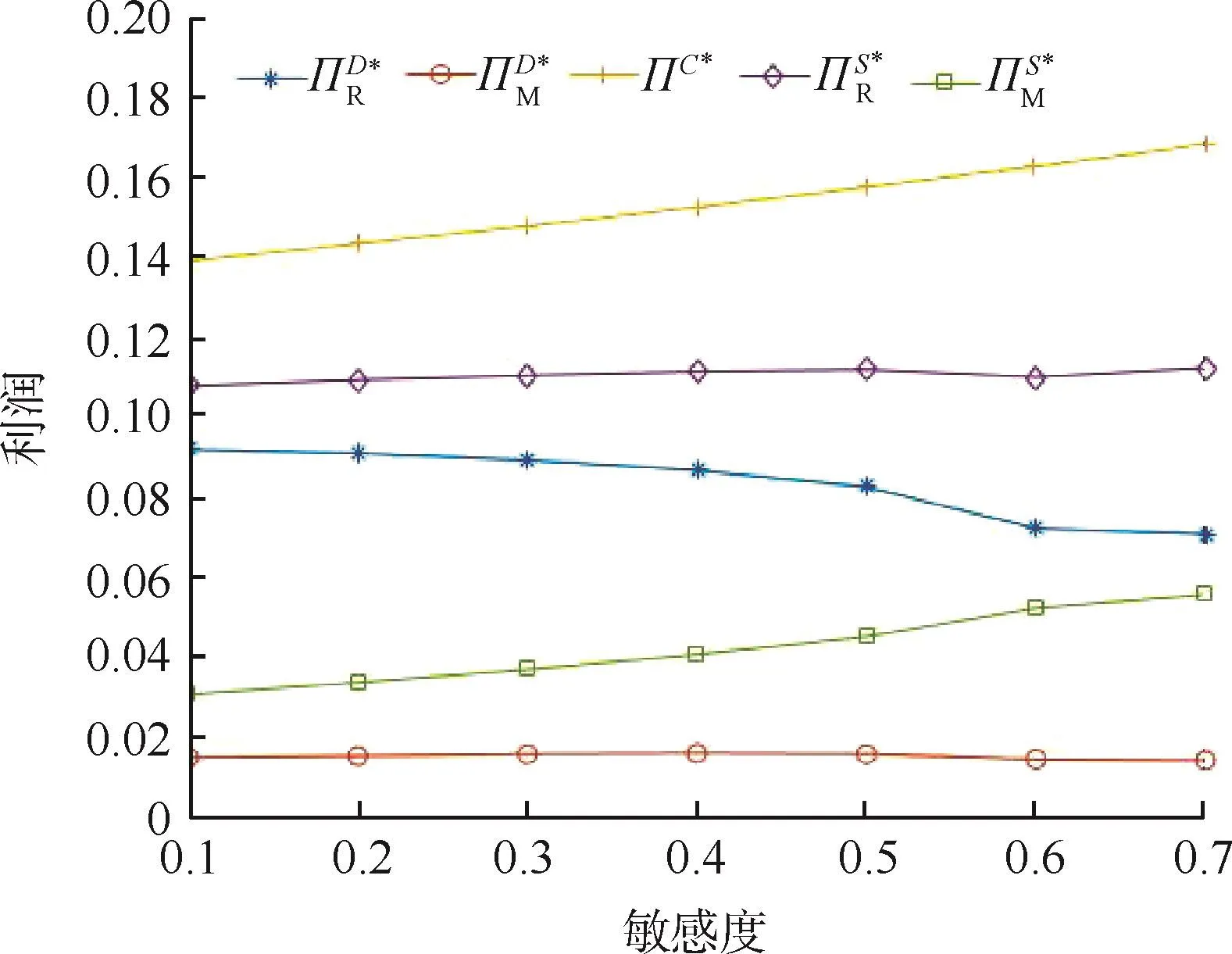
图1 价格敏感系数对利润的影响

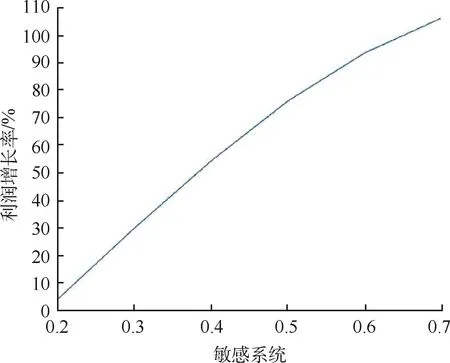
图2 在弹性订单政策下价格敏感度对利润增长率的影响

5 结 论

本文考虑的是在随机生产的基础上,对零售商二次降价模型进行了分析.制造商和零售商进行协商,提出了弹性订单合同使得集中模型下的最优利润得到提升,在分散模型中,利用 Stackelberg博弈理论,求出当制造商作为主导者时,上下游双方的最优决策与集中模型下的最优决策进行比较,并不能达到最优.于是提出了能够使供应链达到协调的新型契约,在一定条件下,可以通过改变参数来实现剩余利润的分配,使得上下游双方在协调模型中的利润能够达到最优.