不同应力状态下多杂质盐岩分数阶蠕变模型参数演化规律研究
易海洋,路乐乐,武志德,张 倩,姬振兴,孙如意
(1.华北科技学院,河北 廊坊 065201;2.中国矿业大学(北京),北京 100083;3.中国石油勘探开发研究院 廊坊分院,河北 廊坊 065007)
1 前言
盐岩凭借其具有低渗透率、较好的流变性和损伤自恢复性能被认为是油气储藏和处理高放射性核废料的理想介质[1-4]。我国地下盐岩资源丰富,具有建立储库的有利条件,但我国盐岩具有单层厚度薄、含夹层较多以及盐岩成分中杂质含量较多等特点[5-6]。目前,盐岩蠕变理论模型主要适用于纯盐岩,而纯盐岩与多杂质盐岩具有明显的力学特性[7-8]。因此多杂质盐岩变形行为及其力学特性引起了广泛的关注。
为保证地下储库在运营过程中的安全性和长期稳定性,国内外学者理论分析、试验、数值模拟等几个方面对多杂质盐岩蠕变进行了大量的研究。周宏伟等[4]通过对含夹层盐岩进行渗透性测试和CT 扫描,发现层状盐岩的结构较为致密,夹层部分不存在缺陷,且在静水压力作用下,试件发生压缩变形。郑雅丽等[7]通过对不同杂质含量盐岩进行压缩试验,发现杂质含量影响岩石的变形能力、弹性模量和抗拉压强度、粘聚力、内摩擦角等物理力学特性。徐素国等[9]对钙芒硝盐岩进行蠕变试验,并总结了钙芒硝盐岩的力学特性。王安明等[10]通过研究杂质颗粒形状、大小、含量、分布方式对含杂质盐岩整体力学特性的影响,总结了杂质含量和力学特性不匹配导致的内部应力集中现象。唐明明等[11]对含夹层盐岩研究,并通过试验分析盐岩试样的破环方式以及其他力学参数。
可见,杂质对盐岩的蠕变行为影响十分显著。多杂质盐岩由于非均质性,在蠕变损伤演化过程中其力学性能会发生明显变化。为此,周宏伟等[12-14]提出了盐岩分数阶蠕变模型,该模型中,考虑了蠕变损伤对材料粘性的影响,能够很好地刻画非均质材料的蠕变损伤演化过程。然而,分数阶蠕变模型由于考虑了蠕变损伤对材料粘性的影响,在不同应力作用下,材料的粘性演化规律是不同的。当前,很少见到关于分数阶蠕变模型在不同应力下的粘性和分数阶阶数演化规律的研究文献。
因此,文章通过开展多杂质盐岩在不同围压下不同应力分级加载蠕变试验,并基于分数阶蠕变模型,对试验数据拟合辨识盐岩分数阶蠕变模型参数,分析参数随应力的变化规律,提出参数随应力的演化模型,进一步拓展分数阶在岩石力学中的应用,丰富多杂质盐岩蠕变变形的研究方法。
2 多杂质盐岩三轴蠕变试验
此次盐岩蠕变试验使用中国石油勘探开发研究院廊坊分院地下储库工程实验室盐穴储库长期运行蠕变试验机CK/Y2014 -01 进行试验,该试验中所用的盐岩试样取自江苏金坛,采用钻孔取芯,由于盐岩易溶于水,而且在潮湿的空气中容易被潮解,则干式锯磨将样品加工成直径100 mm,高为200 mm 的圆柱形试件。试验加载现场和加载平台见图1。

图1 试验加载(a)现场和(b)加载平台Fig.1 Schematic diagram of test loading(a)scene(b)loading platform
试验在室温条件下进行,采取分级应力加载,在不同围压下,分四级应力加载,每级应力为单轴抗压峰值强度的15%、30%、45%、60%,每级加载48 h。盐岩试件样品编号以及尺度参数见表1。根据试验试件的单轴抗压峰值强度、盐岩编号,确定盐岩的三轴蠕变试验的试件标号以及加载应力见表2。由于盐岩蠕变过程中扩容较大,在试验中完成第四级加载后,轴向蠕变和环向蠕变变形量超过了位移计的范围,因此停止了试验。

表1 盐岩样品的基本参数Tab.1 Basic parameters of salt rock samples
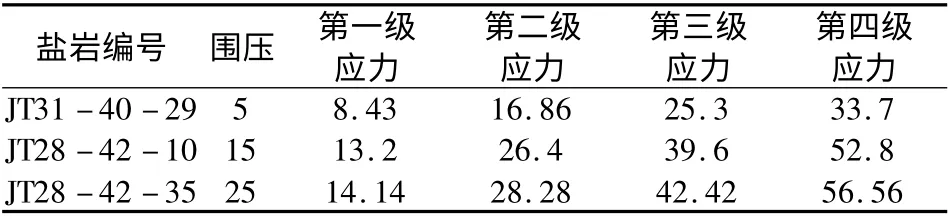
表2 加载方案Tab.2 Loading scheme MPa
3 三维分数阶蠕变模型
根据分数阶微积分的定义,Zhou 等[12]考虑了盐岩蠕变损伤对其粘性的影响,基于西原模型,如图2 所示,修正了Abel 粘壶的蠕变表达式,如:
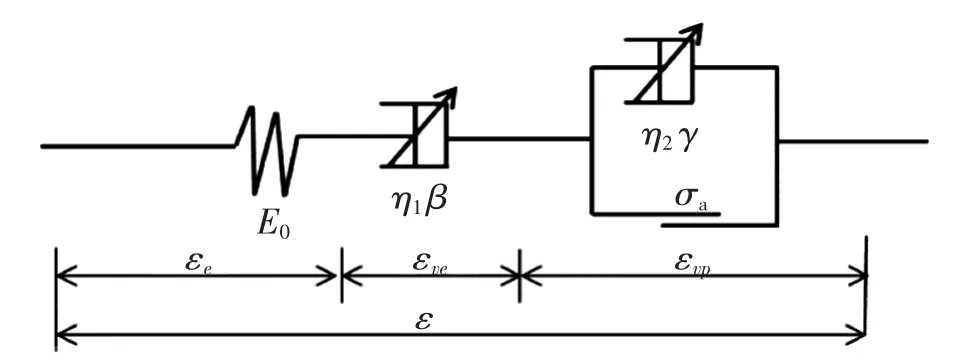
图2 流变本构模型示意图Fig.2 Schetch of rheological constitutive model

式中:β 为求导阶数,η 为黏性系数。当σ 为常数时,对上式(1)两侧进行分数阶积分则有:
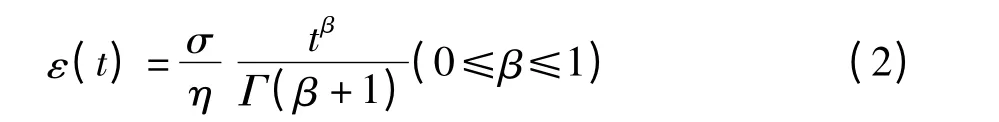
根据西原模型的串联并联关系,即ε =εe+εve+εvp,则盐岩一维分数阶蠕变模型可表示为:
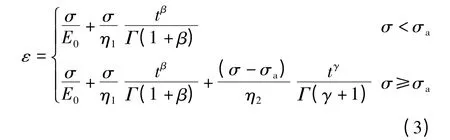
式(3)中,求导阶数的变化可以描述蠕变损伤造成的蠕变率增大现象,如图3 所示。
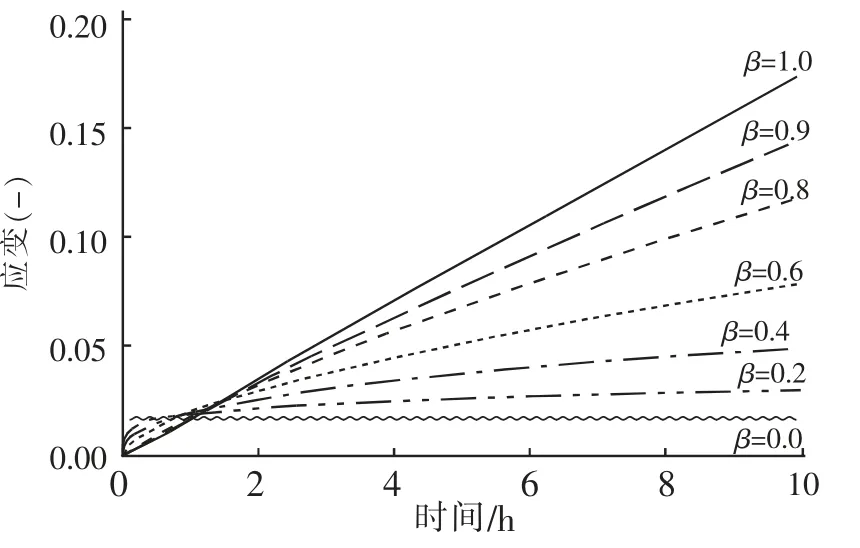
图3 不同求导阶数β 蠕变曲线Fig.3 Creep curves of different derivative orders
因此,分数阶蠕变模型这一良好的性能能够用于描述不同应力加载下,由于不同蠕变损伤引起的蠕变率变化。
文章基于式(3)推导三维分数阶蠕变模型。在三维应力状态下,岩石的弹性本构关系可以用张量形式表示为:

式中:G0为岩石的剪切模量;k0为岩石的体积模量;Sij为偏应力张量;σmδij为球应力张量。其中σm表示平均应力。
球应力张量σmδij产生的应变是弹性应变,因此在求解黏弹性流变时只考虑偏应力张量Sij,则黏弹性体三维本构关系可以表示为:
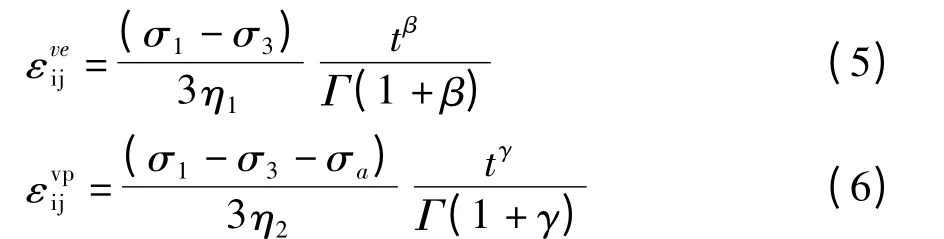
将式(4)~式(6)替换式(3)中的弹性、粘弹性和粘塑性项,得到的三维分数阶蠕变模型如式(7)所示。
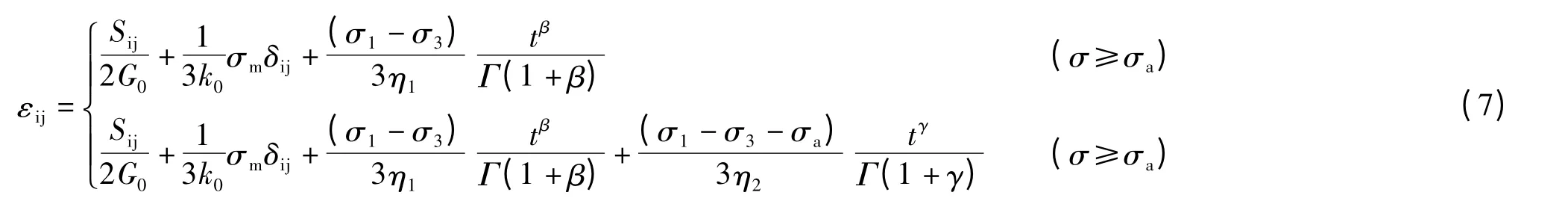
4 不同应力下分数阶蠕变模型参数演化规律
4.1 三维分数阶蠕变模型参数辨识
文章在周宏伟等[15]提出的一维分数阶蠕变模型基础上,将一维分数阶蠕变模型推导出了三维形式。如式(7)所示,开展的盐岩蠕变试验为三轴形式。因此,采用式(7)进行不同应力作用下盐岩分数阶蠕变参数演化规律的研究。试验数据和拟合结果分别如表3 和图4 所示。
由图4 可知,在不同围压作用下,盐岩三轴蠕变试验中各级加载的应变随时间演化曲线经历了典型的初始蠕变和稳态蠕变阶段。随着加载应力的增大,初始蠕变值逐渐增大,表现为加载后蠕变曲线在较长一段时间内的非线性曲线关系,且随着加载应力的增大,蠕变应变增长率逐渐提高,表现为稳态蠕变阶段的应变曲线向上抬升。续表3 (Continue)
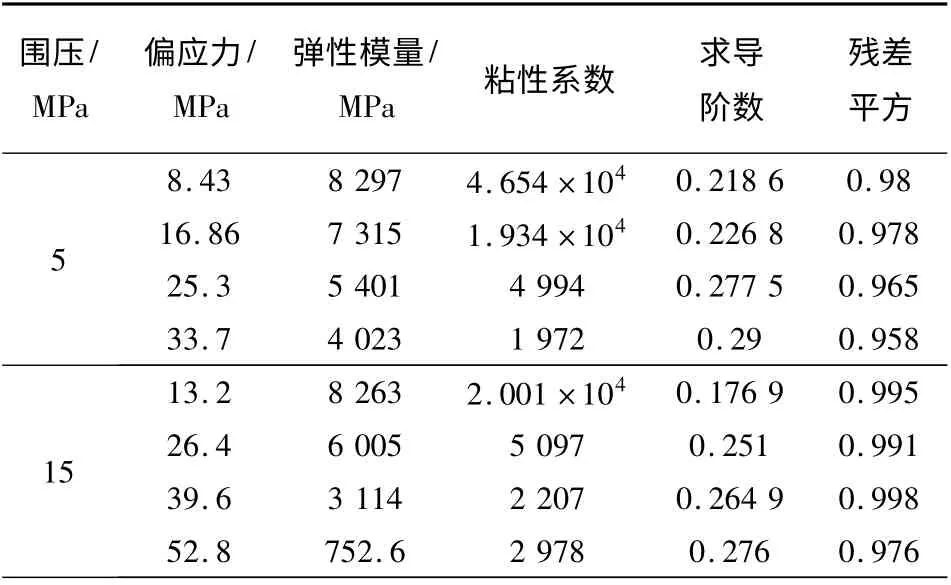
表3 分数阶蠕变模型参数拟合Tab.3 Parameter fitting of fractional creep model
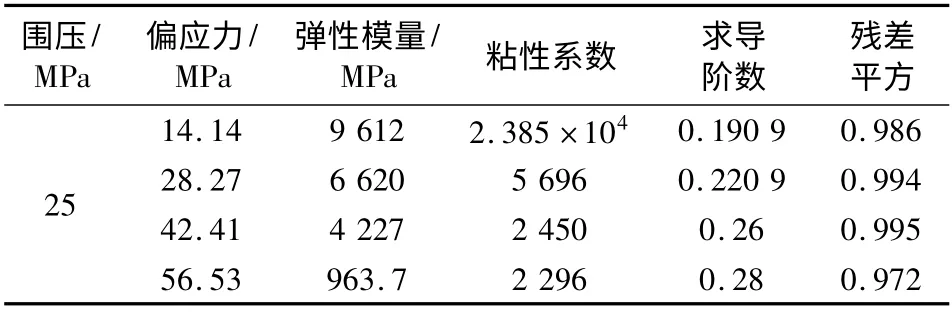
围压/MPa偏应力/MPa弹性模量/MPa 粘性系数 求导残差阶数平方25 14.14 9 612 2.385 ×104 0.190 9 0.986 28.27 6 620 5 696 0.220 9 0.994 42.41 4 227 2 450 0.26 0.995 56.53 963.7 2 296 0.28 0.972
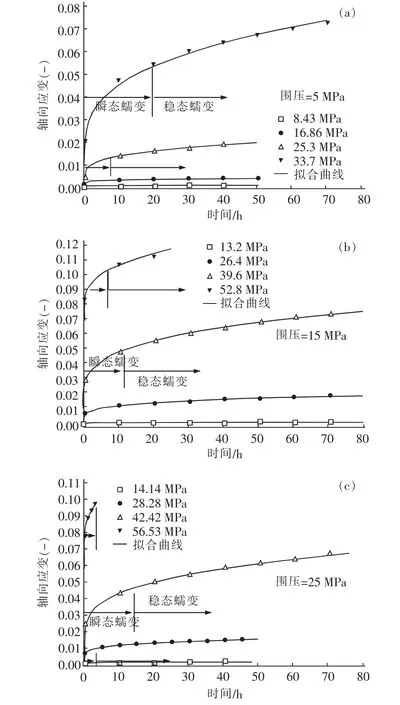
图4 不同应力水平下盐岩蠕变曲线(a)~(c)对应围压分别为5 MPa、15 MPa 和25 MPaFig.4 Creep curves of salt rock at different stress (a)-(c)corresponding to confining pressures of 5 MPa,15 MPa and 25 MPa,respectively
4.2 三维分数阶蠕变模型参数演化规律
拟合得到的参数如表3 所示。由表3 可知,在不同围压作用下,随着加载应力增加,盐岩内部晶体颗粒破坏,盐岩体积变形,弹性模量、粘性系数逐渐减小;分数阶求导阶数逐渐增大,表明加载应力将加速盐岩劣化过程。蠕变模型拟合的残差平方基本都集中在0.97 ~0.99 之间,表明拟合结果能够很好地刻画试验数据的演化趋势。
多杂质盐岩随着应力水平的增加,内部损伤逐渐积累,稳态蠕变阶段缩短,稳态蠕变率逐渐增大,盐岩晶体颗粒之间的粘聚力逐渐降低,变形量进一步增大,盐岩相对更容易进入加速蠕变阶段。
文章研究多杂质盐岩三轴压缩蠕变试验数据,并通过非线性最小二乘法拟合得到分数阶蠕变模型参数如表3 所示。
假定求导阶数β、粘性系数η1以及弹性模量E与偏应力均服从指数分布,可以表示为:
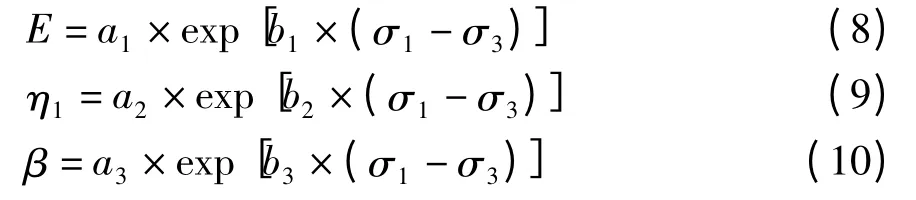
式(8)~式(10)中的a1~a3以及b1~b3为拟合参数,在不同围压作用下,各拟合参数见表4 ~表6,数据拟合效果如图5 所示。
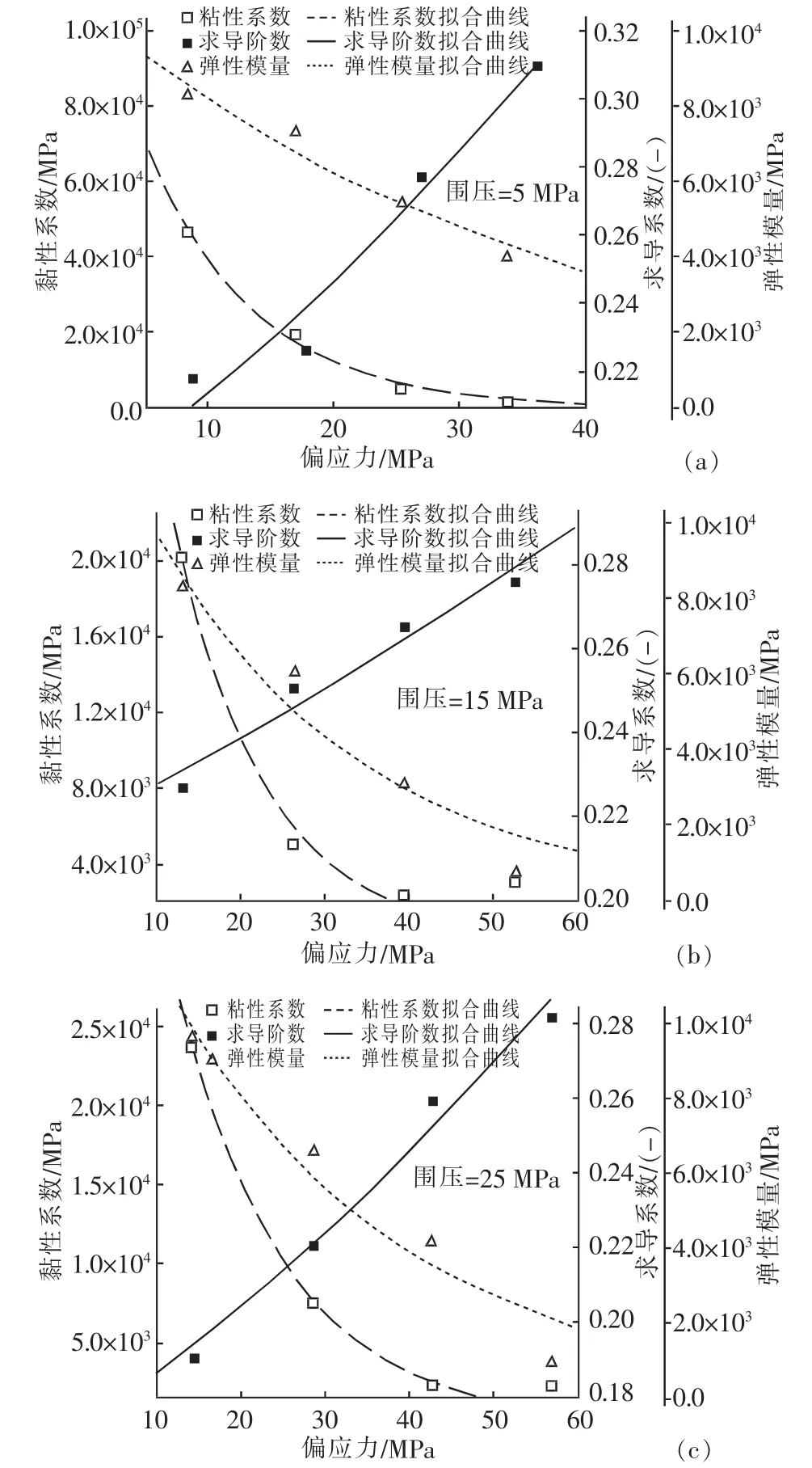
图5 分数阶蠕变模型参数变化规律Fig.5 Parameters variation of fractional creep model
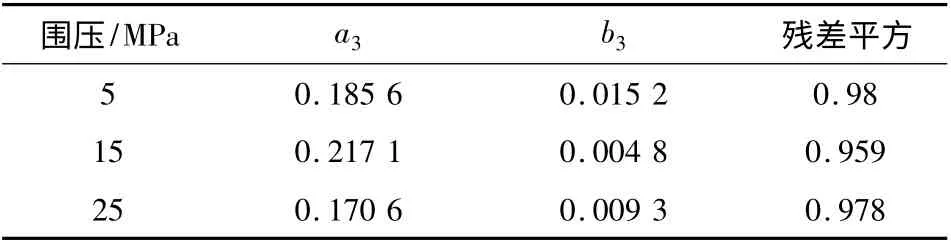
表6 求导阶数演化模型参数拟合Tab.6 Fitted parameters of derivative order

表4 弹性模量演化模型参数拟合Tab.4 Fitted parameters of elastic modulus
由参数演化拟合结果可知,文章所建立的分数阶蠕变模型参数弹性模量、粘性系数、求导阶数的演化模型均为指数型变化,且拟合残差平方介于0.95~0.99,表明建立的参数演化模型能够较好的描述蠕变模型参数随应力的变化规律。

表5 粘性系数演化模型参数拟合Tab.5 Fitted parameters of viscosity coefficient
值得注意的是,弹性模量演化模型和粘性系数模型与文献[16]中Lubby2 盐岩蠕变模型中的粘性系数模型的形式一致,表明文章提出的粘性系数模型具有一定的合理性。
5 结论
通过开展多杂质盐岩在不同围压下不同应力分级加载蠕变试验,并基于分数阶蠕变模型,对试验数据拟合辨识盐岩分数阶蠕变模型参数,并分析模型参数随应力的变化规律,得到如下结论:
1)分数阶蠕变模型能够很好的拟合多杂质盐岩的蠕变行为。
2)随着加载应力的增加,多杂质盐岩分数阶蠕变模型弹性模量、粘性系数呈指数型减小,求导阶数呈指数型增大。
3)文章提出的基于分数阶蠕变模型的多杂质盐岩弹性模量、粘性系数和求导阶数演化模型,该模型能够很好的描述多杂质盐岩蠕变过程中的弹性模量、粘性系数和求导阶数变化过程。同时,文章提出的弹性模量和粘性系数演化模型与Lubby2 模型中的参数演化模型形式一致,表明文章建立的分数阶蠕变模型参数演化模型具有一定的合理性。

