三维振镜激光扫描仪的数学模型构建

闫俊娜，谢凤艳，刘 倩

（安阳学院 数理学院，河南 安阳 455000）

0 引 言

随着激光技术的逐渐成熟，激光扫描技术以快速性、非接触性、实时性和抗干扰性等优势被广泛应用于诸多领域内[1]。振镜式激光扫描系统与以往的机械扫描有所差异，振镜式激光扫描系统利用电流使转子形成偏转[2]，激光束照射在振镜上，由振镜的偏转使激光束发生偏转，在扫描视场内获取激光轨迹[3]。传统基于变形监测理论的三维振镜激光扫描系统数学模型[4]，通过构建变形监测的理论误差模型，用实验验证误差模型，从而获取三维振镜激光扫描系统的数学模型，没有校正三维振镜激光扫描系统中存在的误差，扫描结果误差较大。针对这一问题，本文构建新的三维振镜激光扫描系统数学模型，分别校正系统中的测距误差与角度误差，提高扫描系统的扫描精度。

1 三维振镜激光扫描系统的数学模型

1.1 构建三维振镜激光扫描系统的数学模型

图1 中描述的是三维振镜激光扫描系统工作原理。利用扩束镜将激光器发射的激光扩束，使激光转变为平行光；平行光进入动态聚焦镜完成聚焦，达到标准强度的激光将聚集为激光束[5]，通过X，Y 振镜对激光束实施两次反射，使激光束投射至工作面内，生成工作面内的扫描点。通常情况下，利用两个振镜间的偏移转动能够完成任意三维图形的二维平面转换[6]。

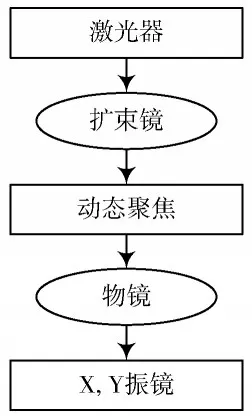
图1 三维振镜激光扫描系统工作原理图

图2 中所描述的是双振镜扫描系统，经动态聚焦镜凝聚的激光束由x 轴振镜，反射至y 轴振镜，再由y 轴振镜反射至工作面内的m(x,y) 处。x 轴振镜和y 轴振镜的偏转角分别用λx和λy表示，在λx=0，λy=0 的条件下，激光的光斑出现在工作面的原点位置O( 0,0 )处，同时，位于行程中心平衡点的动态聚焦镜的聚焦位置同样是O( 0,0 )处。这时以聚焦镜为起点，以工作面内的光斑处为终点的光程L 为：

式中g 和n 分别表示y 轴振镜与工作面间的垂直距离和x 轴振镜与y 轴振镜间的垂直距离。在激光光斑位于工作面内任意点m( x,y )的条件下[7]，其x 轴转角和y 轴转角如图2 所示。

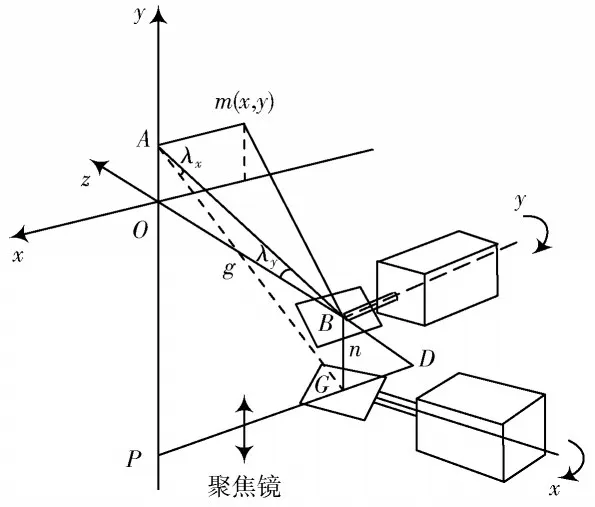
图2 双振镜扫描系统

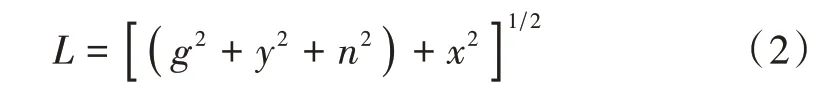
光程差如下：

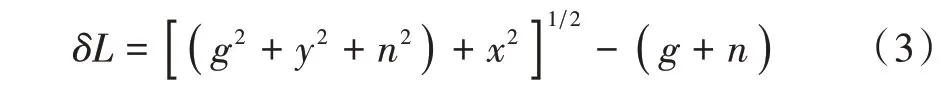
由此得到三维动态聚焦振镜扫描系统的数学模型，包括：

以及式（2），式（3）。

1.2 误差分析与矫正

三维振镜激光扫描系统中包含了多种固有误差[8]，这些误差使得数学模型在控制系统工作时出现较高的误差，因此需要分析和校正这些误差。

1.2.1 测距误差

激光测距仪大体包括两种：一是相位法激光测距仪，利用发送信号同回波信号间的相位差[9]，间接测量距离；二是脉冲法激光测距仪，利用发送信号同回波信号间的时间差[10]，获取障碍物同激光测距仪之间的距离J，具体计算过程为：

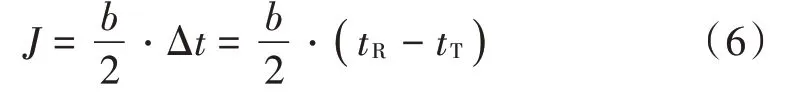
式中b，tR和tT分别表示大气内光波的传播速度、回波信号的时间和发送信号的时间。

采用相位法激光测距仪测量距离时，精度受相位差测量精度的影响[11]，当前普遍采用的数字鉴相器技术的分辨率极限值和测距精度极限值分别为0.001 7°和±1 mm，能够满足测量精度的要求，然而测量速率较差，不能实现实时扫描。相比之下，脉冲法激光测距仪的测量速率能够实现实时扫描，但测量精度受tR-tT的测量值影响，通常情况下，tR-tT的时间差是皮秒级。脉冲法激光测距仪的测量范围和测量速率极限值分别为0.5～3 000 m 和10 kHz，完全可以满足实际应用中的要求[12]，但测距精度是±60 mm，误差较高。为了解决激光测距仪测距误差的问题，本文提出一种速度与精度交换的方法[13]。

若v 和±ϕ 分别表示激光测距仪的极限测量速率和精度，那么测距误差服从正态分布，用表示。用X1,X2,…,Xn描述一固定位置多次定点测距的误差，那么能够判断X1,X2,…,Xn出自于正态总体分布的随机样本，此样本的均值和方差分别是µ和ϕ2。同时，抽样该样本均值能够得到，也服从正态分布，均值和方差分别是µ和ϕ2n，通过描述测距误差[14]。运算得到距离值的平均值，运算次数为n，那么测距仪的输出速率将会下落至v n，然而精度会相应上升至表1 中描述的是脉冲法激光测距仪的测量距离值在n 次平均运算后，测量速度同精度间相关性的几组代表值。

1.2.2 角度误差

在三维激光扫描系统内，x 轴振镜与y 轴振镜均能够影响激光光束的偏转角度。电机真实移动角度同计算获取的移动角度两者间产生非线性误差的原因有可能是电机角位移的固有误差造成，也可能是扫描镜的机械振动造成[15]。由于造成角度误差的原因较多，从理论层面上分析，校正误差较为复杂，难以全面分析，因此在分析、校正角度误差的过程中，多采用根据真实扫描数据构建补偿曲面或校正表的方法校正角度误差。本文针对三维振镜激光扫描系统中存在的角度误差，提出基于最小二乘法获取角度误差的方法[16]。

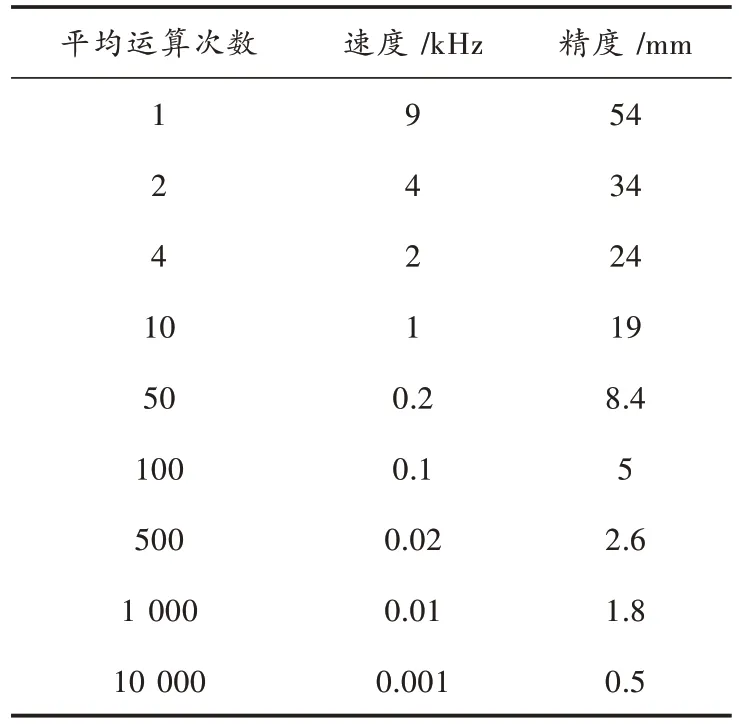
表1 测量速率与精度的关系

分别用l( x,y ,z )和p( x,y ,z )描述三维扫描理想图和真实获取存在误差的畸变图，理想图与畸变图间有影射关 系，即p( x,y ,z )=h( l( x ,y ,z ))。利用真实扫描数据获取影射关系h，再运算角度误差。将多次扫描某固定对象获取的距离值代入笛卡尔坐标系内，获取工作面内某点A( xa, yb,zc)的坐标值，分别用( x1, y1,z1)，( x2, y2,z2)，…，( xn, yn,zn)描述，这n 个点均为A 点的观测点。依照最小二乘原理运算距离这n 个观测点最近的点A′( x0, y0,z0)，点A′( x0, y0,z0)被称为点A 的平均位置。假设点A′( x0, y0,z0)为圆心位置，那么n 个观测点均在圆内。在观测点中随意挑选点( xi, yi,zi)和( xj, yj,zj)，且1 ≤i,j ≤n，能够得到这两个点到圆心A′( x0, y0,z0)的距离一致，由此获取n-1个等式，用误差方程的形式描述为：

设未知数的个数大幅度低于测试次数，也就是3 ≪n，那么AX=k 表示超定方程，不存在精确解。依照最小二乘原理，通过计算获取点X0，使不同观测点至拟合曲面距离的平方和最小，也就是l( X0)=对式（7）求取最小二乘解时采

用SVD 分解法，则有：

式（7）内，A 表示列满轶矩阵，包含正奇异值3 个，即ϕi( i= 1,2,3 )，A 的奇异值分解可用描述，U，V 分别是n 阶酉矩阵和3 阶酉矩阵，F=diag( ϕ1,ϕ2,ϕ3)。U 的前三列组成的矩阵用U1表示，也就是U=( U1,U2)，按照3 阶酉矩阵 范 数 的 酉 不 变 性，可得：

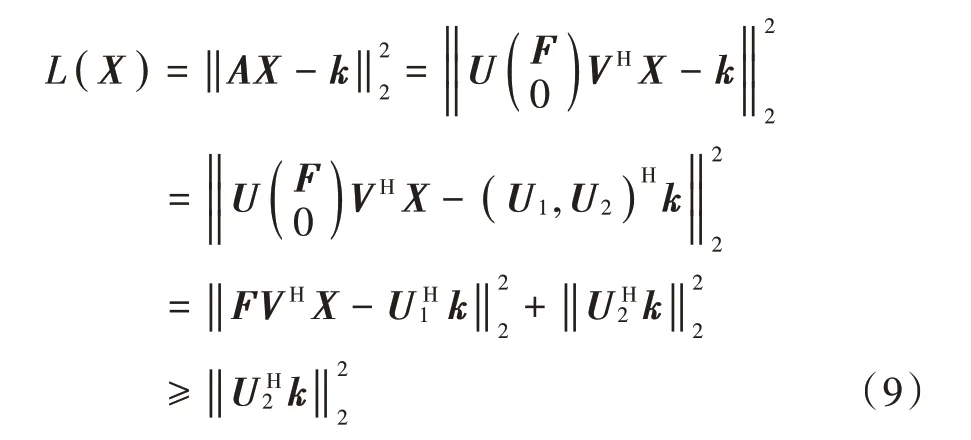
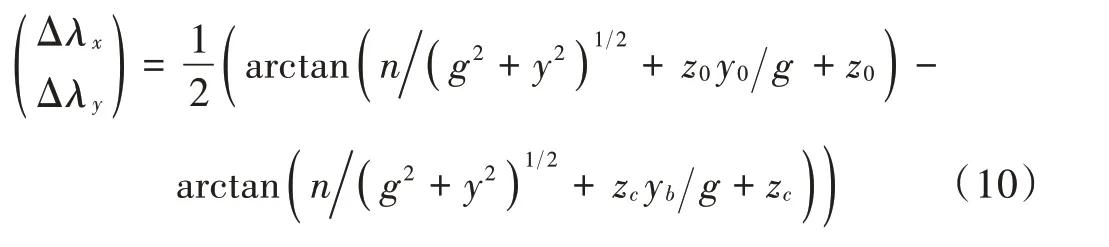
式（10）内，点A(xa,yb,zc)处电机移动的角度误差用Δλx和Δλy表示，此误差受驱动器、电机特性等固有特征作用，所以校正理论角度时，能够充当系统固有误差，获取电机真实移动角度。

2 实验结果与分析

ZEMAX 软件能够实现光学系统内的建模、分析等功能，涵盖了光学设计过程中所需的全部功能，同时具有容差性能好、速度快、灵活性强的优势。因此，实验采用ZEMAX 软件对本文构建的三维振镜激光扫描系统的数学模型实施模拟仿真分析。利用ZEMAX 软件本文模型控制下三维振镜激光扫描系统模拟焦距为40 mm，320 mm，560 mm 的3 个聚焦透镜，第一聚焦透镜和第二聚焦透镜间的距离为360 mm，第二聚焦透镜和第三聚焦透镜间的距离为0 mm。对比ZEMAX 软件仿真结果，通过计算获取聚焦点移动距离ΔS 以及第一透镜移动距离Z 间的关系值，结果如表2 所示。

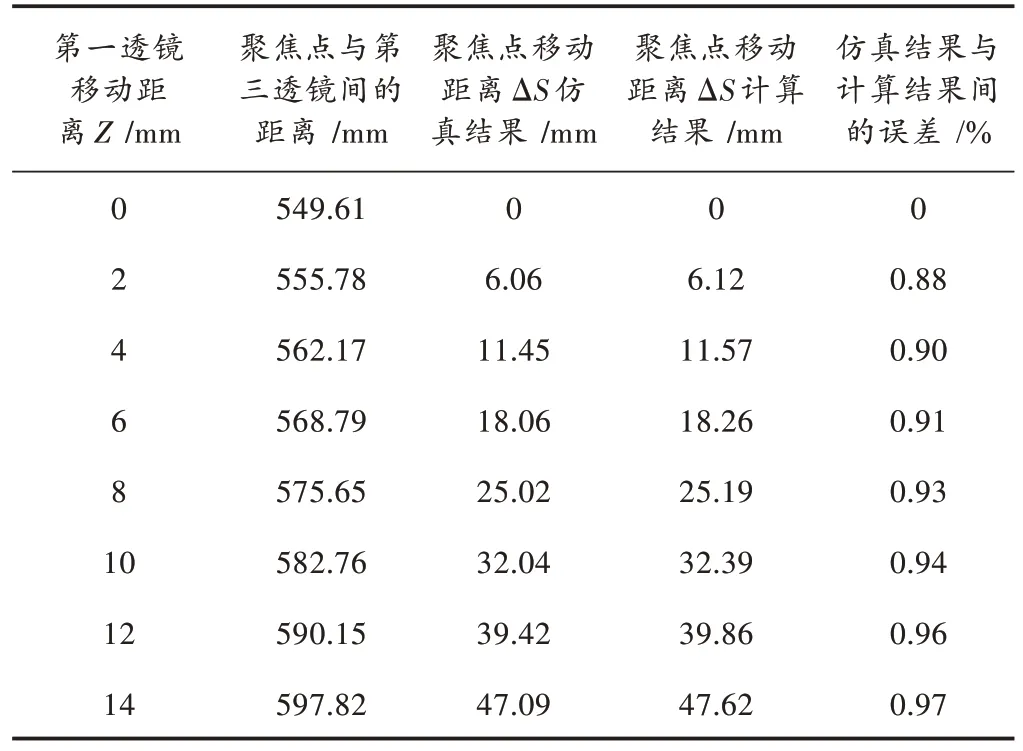
表2 ZEMAX 软件仿真参数表

图3 中描述的是第一透镜移动距离Z 与聚焦点移动距离ΔS 间的关系。

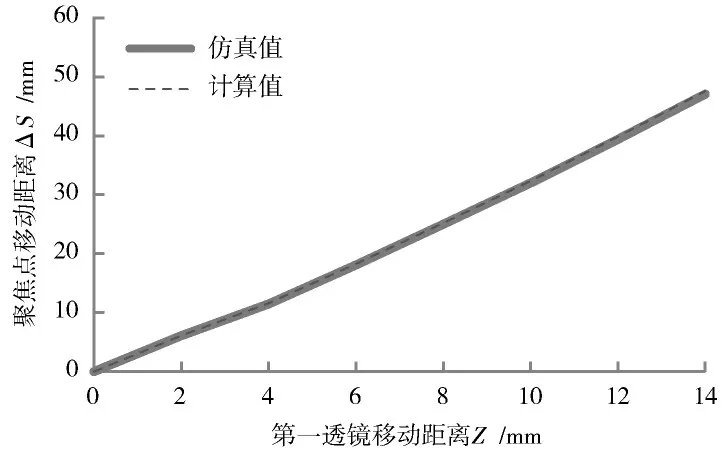
图3 第一透镜移动距离Z 与聚焦点移动距离ΔS 间的关系图

分析表2 和图3 能够得到：第一透镜移动距离Z 与聚焦点移动距离ΔS 间存在非线性关系，且两者间的关系接近直线，说明第一透镜移动距离Z 与聚焦点移动距离ΔS 均为匀速状态，仿真结果与计算结果间的误差未超过1%。实验结果表明，本文模型控制的三维振镜激光扫描系统具有可行性。

实验为测试本文模型控制的三维振镜激光扫描系统中激光电流与功率之间的关系，控制激光器驱动电源电流的变化，使阈值电流从7 A 提升至31 A，采用激光功率计获取不同电流值下激光功率，提取不同的激光功率值绘制表3，根据表3 绘制折线图如图4 所示。

图4 不同激光电流值下的激光功率值

分析表3 和图4 能够得到：在不同的电流值下，本文模型控制的三维振镜激光扫描系统的激光器输出较为平稳，最大输出功率达到50 W 左右。同时，不同电流值下，第一次实验功率的平均值为24.83 W，第二次实验功率的平均值为24.95 W，第三次实验功率的平均值为24.74 W，第四次实验功率的平均值为24.93 W，4 次实验结果变化不大，基本一致。从4 次实验结果能够看出，当激光器电流大小发生变化时，激光器功率随着电流的增大逐渐提升，两者间保持线性关系，说明本文模型控制的三维振镜激光扫描系统具有较高的稳定性。

实验为验证本文模型控制下三维振镜激光扫描系统的校正效果，选取的实验对象采用本文模型和基于变形监测理论的三维振镜激光扫描系统的数学模型。本文模型控制下，三维振镜激光扫描系统进行校正测距误差时，平均值运算次数为4；校正角度误差时，根据电机真实移动的角度获取校正后的距离值。不同模型的实验结果如图5 所示。

分析图5 能够得到：本文模型控制下的三维振镜激光扫描系统测距过程中，获取的测量值与实际值基本一致，误差控制在1.5 mm 之内；而基于变形监测理论数学模型控制下的三维振镜激光扫描系统获取的测量值与实际值之间的误差在3.1～5.3 mm 之间。检测不同模型的测距角度误差时，本文模型获取的测量值与实际值间的误差控制在1.03°之内，而基于变形监测理论数学模型控制下的三维振镜激光扫描系统获取的测量值与实际值之间的误差在1.79°～3.31°之间。这些实验结果表明，本文模型控制下的三维振镜激光扫描系统校正误差效果较好，可实现高精度的激光扫描。

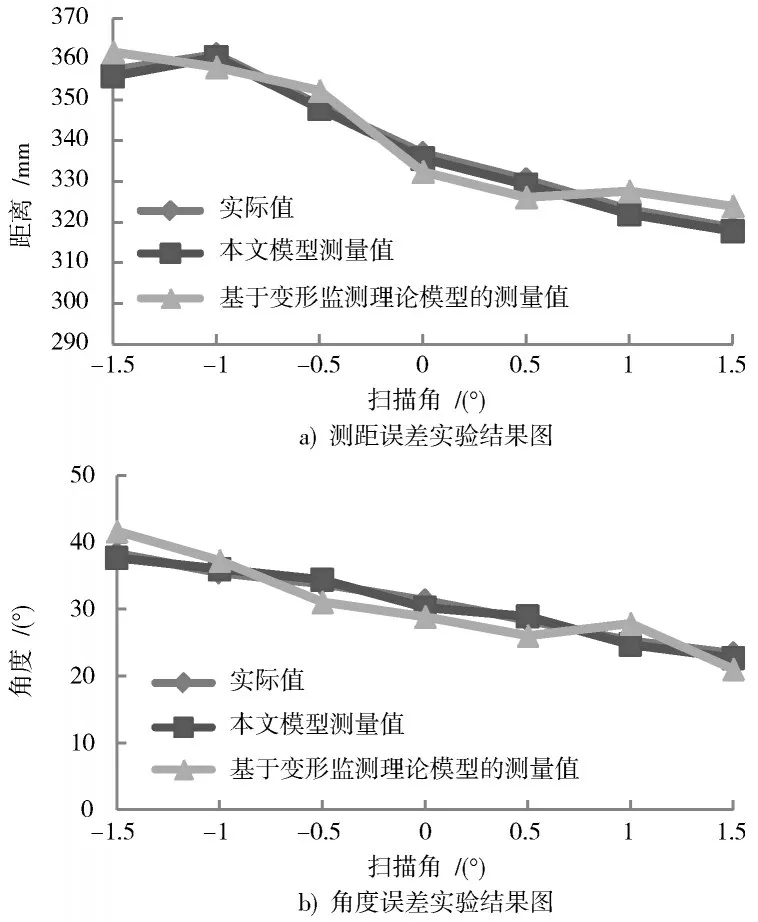
图5 不同模型实验结果图

3 结 语

本文构建了新的三维振镜激光扫描系统的数学模型，从测距误差和角度误差两个方向分析系统误差的来源，并针对不同误差提出不同的校正方法。经实验证明，本文模型仿真结果与计算结果间的误差低于1%，本文模型控制的三维振镜激光扫描系统具有可行性；不同电流值下，4 次功率实验的平均值分别为24.83 W，24.95 W，24.74 W 和24.93 W，且激光器功率随着电流的增大而增大，呈线性关系，说明本文模型控制的三维振镜激光扫描系统具有较高的稳定性。本文模型控制下的三维振镜激光扫描系统测距误差和角度误差分别低于1.5 mm 和1.03°。实验结果表明，本文模型能够有效地控制三维振镜激光扫描系统顺利工作，且误差校正效果较好，可提高三维振镜激光扫描系统的扫描精度。